考虑“路-车-源-荷”多重不确定性的交通网与配电网概率联合流分析

方晓涛，严 正，王 晗，徐潇源，陈 玥，许少伦

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学），上海市 200240；2. 香港中文大学机械与自动化工程系，香港 999077）

0 引言

电动汽车的应用能够有效串联配电网清洁电力生产和交通网低碳能源消费［1］，是保障“碳达峰、碳中和”目标实现的重要途径。随着电动汽车大规模推广应用，交通网与配电网的耦合运行特征日益显著［2］，并受到交通网与配电网多重不确定性的影响。量化分析不确定性因素的影响，对提升交通网运行的可靠性和配电网运行的安全性具有重要意义。

以电动汽车的充电行为作为交互纽带，交通网与配电网耦合运行特征体现在：1）交通网的拥堵状况与充电站电价影响电动汽车用户的驾驶行为和充电站点的选择，从而改变配电网内充电负荷需求；2）大规模充电负荷的时空分布特性直接影响配电网潮流，同时改变充电站的充电电价，进而影响交通流分布。对上述交通网车流与配电网潮流相互影响的耦合运行方式进行建模并获得“物质-交通流”与“能量-电力流”的联合流结果，是目前国内外学者关注的热点问题。文献［3-5］分别以网络均衡模型与最优潮流模型刻画交通流与电力流，得到交通-电力耦合系统的联合流结果；文献［6］计及交互的交通流与电力流，构建了交通网与配电网耦合系统的网络均衡模型并提出了相应求解方法；文献［7-8］分别通过变分不等式与博弈论分析了耦合系统运行均衡状态的存在性与唯一性。以上述交通网与配电网联合流模型为基础，不少学者也开展了耦合系统的风险评估［9］、联合规划［10］等相关研究。

然而，实际交通-电力耦合系统内存在大量不确定性因素，上述文献所获得的交通网与配电网联合流结果尚未考虑多重不确定性的影响。对于交通网而言，道路通行可用容量易受到车辆事故、道路施工等随机事件的影响［11］；电动汽车用户的出行需求、车辆的充电需求受到天气、环境温度等因素影响［12］；多变的道路通行情况（“路”）、随机的车辆用户行为（“车”）成为交通网运行的主要不确定性因素［13］。对于配电网而言，间歇性的分布式可再生能源发电（“源”）、波动性的电力负荷需求（“荷”）直接影响配电网节点注入功率，并造成配电网运行状态的显著改变。“路-车-源-荷”多重不确定性将伴随着交通网与配电网的不断交互传播不确定性，并影响耦合系统运行。在此情况下，获得耦合系统的联合流计算结果将面临如下问题：

1）考虑“路-车-源-荷”多重不确定性，如何构建交通网与配电网的耦合运行模型，并实现不确定性环境下交通-电力联合流的量化表征；

2）如何量化评估“路-车-源-荷”多重不确定性因素对交通流、电力流的影响程度，以反映不确定性传播下交通网与配电网的交互影响。

针对上述问题，本文提出了考虑“路-车-源-荷”多重不确定性的交通网与配电网概率联合流分析方法。首先，分别建立了考虑“路-车”不确定性因素的概率交通分配模型和考虑“源-荷”不确定性因素的概率最优潮流模型，并实现不确定性环境下交通网与配电网的概率联合流计算；然后，引入基于Sobol’法的全局灵敏度分析方法，量化多重不确定性因素对交通网与配电网耦合运行的影响，辨识关键不确定性因素；最后，通过耦合算例仿真计算验证了所提方法的有效性。

1 考虑“路-车”不确定性因素的概率交通分配模型

1.1 交通网“路-车”不确定性建模

本文采用概率分布函数表征交通网“路”“车”不确定性因素的随机特征。对于“路”而言，随机变量包括道路容量和道路环境温度；对于“车”而言，随机变量包括车辆出行需求和不同出行阶段电池荷电状态（SOC）。给定交通网络GT(N，A)，其中N为节点集合（本文中交通网节点包括车流交汇处和车辆充电时充电站所在处），A为道路集合。设定S为充电站节点集合，且S⊆N；W为所有汽车的起点-终点（O-D）对的集合；KGw和KEw分别为燃油汽车和电动汽车在O-D 对w∈W之间的路径集合。对交通网“路”“车”不确定性因素建模如下：

1）道路容量

道路容量指道路正常通行下的最大车流量。在交通网运行中，对于道路a=(i，j)∈A（i，j∈N且i和j分别为道路a的起点和终点），其容量的随机波动ξC，a可采用正态分布刻画［14］，记为ξC，a～N(μC，a，σC，a)，其中，μC，a和σC，a分别为ξC，a的均值与标准差。因此，ξC，a的概率密度函数可表示为：

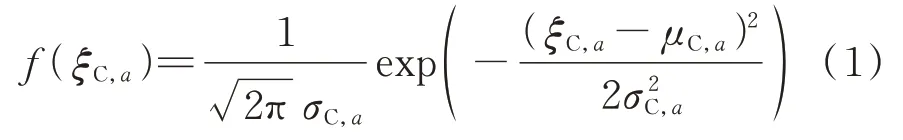
2）道路环境温度

交通网内环境温度本身具有较大不确定性，文献［15］指出环境温度的随机特征可利用正态分布刻画。由于道路环境温度会直接影响电动汽车电池的各项属性（充、放电效率等），同时也与用户是否使用空调等决策行为相关，因此，本文根据FleetCarma公司在北美地区收集的用户出行记录数据，进一步构建了电动汽车能耗率ϖ与环境温度ξT之间的函数关系［16］：

式中：n为幂指数；bn为给定系数，其数值如附录A 表A1 所示。

3）汽车出行需求

汽车出行需求指O-D 对间的移动需求，燃油汽车和电动汽车在O-D 对w之间出行需求量的随机波动ξGN，w和ξEN，w可采用正态分布刻画［17］。

4）电动汽车电池初始SOC

由于从起点出发时电动汽车电池的初始SOC各不相同，若统一采用一个概率分布函数刻画不同电动汽车初始SOC 的随机特征会导致较大误差。为提高建模的准确性，本文将O-D 对w之间起点处的电动汽车分为Tw个类别，各个类别内所有电动汽车的电池初始SOC 采用固定数值近似替代。各个类别内的电动汽车数量占比记为ξS，w，t，t=1，2，…，Tw，所有类别占比总和为1，即

5）电动汽车充电结束时的SOC

电动汽车用户在充电站的停留时间具有一定的随机性，在充电结束时电动汽车并不一定能准确完成预计的充电目标。本文假定电动汽车充电结束时的SOC（记为ξF）近似服从正态分布［18］，且该分布的均值与预计的充电目标相关。

1.2 交通网概率交通分配模型

交通分配指的是将各个O-D 对间的车辆出行需求量按照一定的准则分配到交通网的各个道路上，并得到交通网的流量分布情况。静态交通分配模型是常用的交通流计算模型，其针对某一较长时段内的交通需求进行分配，所得到的各个道路交通流量为该时段内的平均交通流量。在静态交通分配模型的基础上，本文考虑交通网中的“路-车”不确定性因素，提出概率交通分配模型用于获得交通流的概率统计特征。其中，本文所提概率交通分配模型中同时考虑了燃油汽车与电动汽车的出行成本，并做如下说明：1）不考虑燃油汽车的油耗因素，燃油汽车的出行成本仅包括出行时间成本；2）电动汽车的出行成本不仅包括道路行驶的时间成本，还包括在充电站的充电费用和充电时间成本。

1）随机道路容量下道路的通行时间

考虑道路容量的随机波动，对于道路a∈A，采用含随机道路容量波动的美国联邦公路局（BPR）函数来描述车辆通行时间ta与车流量xa之间的关系［6］：

式中：t为道路a在车流量为0 时的通行时间；ca为道路a的基准容量。

2）拥堵效应下电动汽车的充电花费时间

电动汽车在充电站花费的时间包括排队时间和充电时间。对于排队时间，本文考虑拥堵效应的影响［19］，采用如下函数描述电动汽车在充电站s的排队时间ts与等待充电的车流量xs之间的关系：

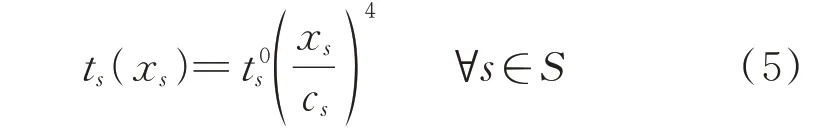
电动汽车在充电站s的充电时间为：

式中：ts，k，w和Fs，k，w分别为O-D 对w之间路径k上电动汽车在充电站s的充电时间和充电量；Ps为充电站s的充电功率；η为充电效率。

3）基于用户均衡准则的概率交通分配模型

基于用户均衡（UE）准则（即Wardrop 第一准则）［20］，考虑交通网“路-车”不确定性的影响，建立概率交通分配模型如下：

式中：cT为交通网所有汽车用户的出行成本；ω为出行时间等效成本的转化系数；λs为充电站s的充电电价；和分别为燃油汽车和电动汽车在O-D 对w之间路径k上的车流量；为燃油汽车在O-D 对w之间的出行需求基准量；为电动汽车在O-D 对w之间的出行需求基准量；γs，k，w为电动汽车在O-D对w之间路径k与充电站节点s的关联系数，当路径k上的电动汽车需要在充电站s充电时，γs，k，w为1，否则为0；k，w和k，w分别为燃油汽车和电动汽车在O-D 对w之间路径k与道路a的关联系数，当路径k∈包含道路a时，，k，w为1，否则为0，当路径k∈包含道路a时，k，w为1，否则为0。

上述模型的决策变量为各O-D 对汽车在各个路径上的车流量，目标函数由4 项构成：第1项为交通网中所有汽车道路通行时间的等效成本；第2、3 项分别为所有电动汽车在充电站排队时间与充电时间的等效成本；第4 项为所有电动汽车的总充电费用。约束式（8）至式（11）为燃油汽车与电动汽车在各个O-D 对之间的路径车流量约束；约束式（12）和式（13）分别表示道路、充电站的车流量与路径车流量之间的关系。求解上述概率交通分配模型即可得到概率交通流结果。

1.3 交通网车辆最优路径生成

为求解上述概率交通分配模型，需要先获取所有可能的最优路径集合和。实际电动汽车选择路径时，除了考虑出行成本外，还需要顾及电池SOC 能否支撑完成全部及后续行程。因此，电动汽车的路径规划与充电决策是相互关联的，本文将其作为一个整体来考虑，在确定电动汽车最优路径时相应考虑充电决策信息，包括其是否在充电站充电、充电时间与充电量等。

本文通过建立并求解优化模型来生成可能的最优路径，其原理是寻找一条当前交通流分布下（道路车流为、充电站车流为），燃油汽车或电动汽车出行成本最小的可行路径。

1）燃油汽车最优路径生成模型

对于O-D 对w之间的燃油汽车，生成路径k的优化模型目标函数为：

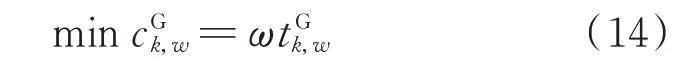
其中

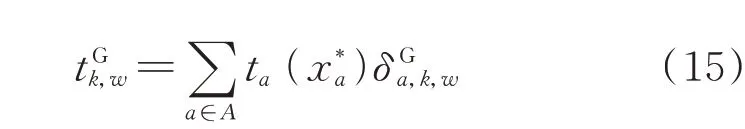
2）电动汽车最优路径生成模型

对于O-D 对w之间的电动汽车，生成路径k的优化模型目标函数为：

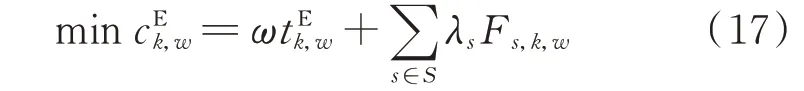
其中

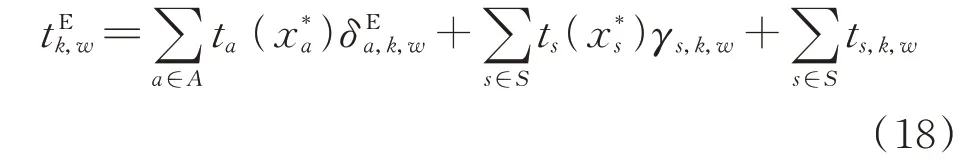
式中：c为该路径的总出行成本；t为该路径的总出行时间，包括道路通行时间、充电站排队时间与充电时间。

模型的约束条件如下：

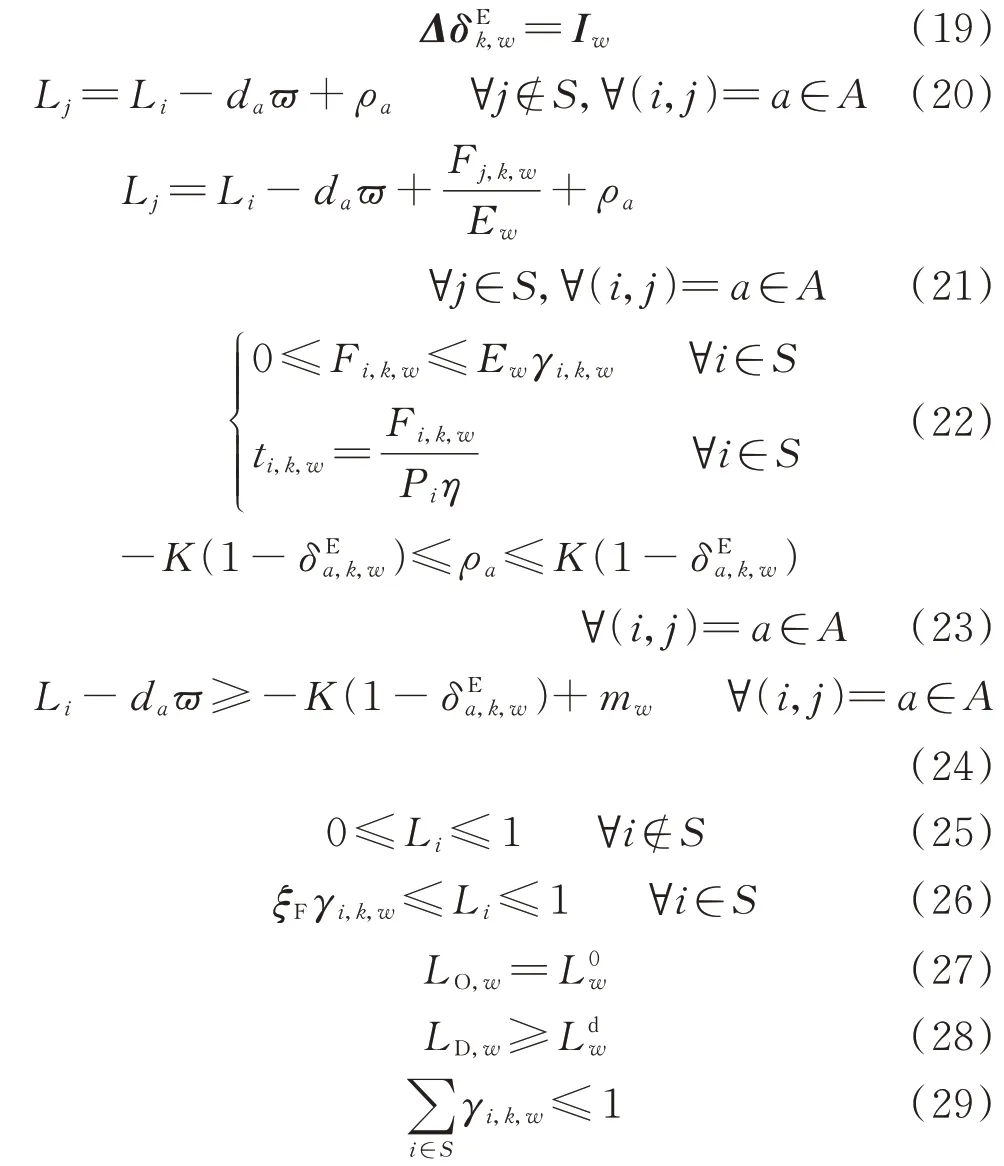
在传统的电大远程教学过程中，是通过内容的传输来实现远程教学，需要学生进行下载操作才能对教学视频、音频进行观看。即通过WEB服务器传输到浏览者的计算机中，下载后存储到硬盘中再对文件进行观看，这些文件包含图片、视频、音频等内容，一些容量过大的文件会使观看过程中出现各种问题，存在声音与视频不相符的情况，影响观看的效果。该做法将导致计算机以及WEB的负荷增大，并且使文件的时效性降低。并且传统的教学过程中无法实现学生与远程教师的实时互动，不能对问题进行及时解决，大数据技术的应用能够增强多媒体在教学过程中起到的作用，确保教师以及学生之间交流的实时性，同时通过邮件以及平台留言等方式也可以解决以上问题。

上述约束条件中，式（19）确保了路径的可行性；式（20）和式（21）为电动汽车在通过道路、充电站后的电池SOC 平衡约束；式（22）为电动汽车在充电站的充电量与充电时间约束，当路径与充电站节点的关联系数γi，k，w为0 时，电动汽车的充电量与充电时间也为0；式（23）为辅助变量约束，当路径与道路的关联系数，w为0 时，辅助变量近似无约束，当，w为1 时，辅助变量为0；式（24）至式（28）对各个节点处电动汽车电池SOC 进行限制；式（29）确保电动汽车在该路径上最多只在一个充电站充电。

2 考虑“源-荷”不确定性因素的概率最优潮流模型

2.1 配电网“源-荷”不确定性建模

对于含分布式可再生能源的配电网，间歇性可再生能源发电（风电、光伏发电）与波动性负荷是影响其运行的主要不确定性因素。给定配电网GD(EN，EL)，其中EN为节点集合，EL为支路集合。配电网与上级电网的联络节点为平衡节点，EG为电源所在节点集合（包含平衡节点），且EG⊆EN。本文将分布式可再生能源等效为功率注入方向相反的负荷，其所在节点不包含于电源节点集合EG中。进一步，采用概率分布函数，对配电网“源”“荷”不确定性因素建模如下：

1）可再生能源不确定性建模

风电机组、光伏电池的输出功率分别与风速、光照强度密切相关，在长时间尺度下，风速近似服从Weibull 分布［22］：

式中：v为风速；ξk和ξc分别为Weibull 分布的形状参数和尺度参数。

光照强度近似服从Beta 分布［23］：

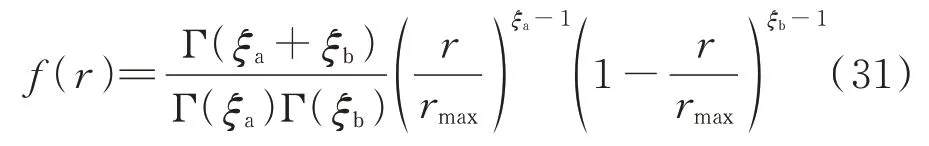
式中：r和rmax分别为光照强度和最大光照强度；ξa和ξb为Beta 分布的形状参数；Γ(·)为伽玛函数。

基于风速与光照强度数据，依据文献［24］的函数关系能够得到对应的风电机组与光伏电池有功功率。进一步，通过节点i∈EN处可再生能源的功率因数和有功功率PR，i可得到其无功功率QR，i。

2）负荷不确定性建模

配电网中除充电站充电负荷外其他负荷的有功功率PB，i（i∈EN）可认为近似服从正态分布［24］，记为PB，i～N(μB，i，σB，i)，其中，μB，i和σB，i分别为PB，i的均值和标准差。PB，i的概率密度函数可表示为：

通过节点i处除充电站充电负荷外其他负荷的功率因数和有功功率PB，i可得到其无功功率QB，i。

2.2 配电网概率最优潮流模型

相比于输电网，配电网具有特殊的网络特性，如线路电阻与电抗的比值较大、辐射性结构等，一般采用交流最优潮流算法获得配电网最优潮流。在此基础上，本文考虑不确定性“源-荷”的影响，建立了配电网概率最优潮流模型，以获得配电网最优潮流的概率统计特征：

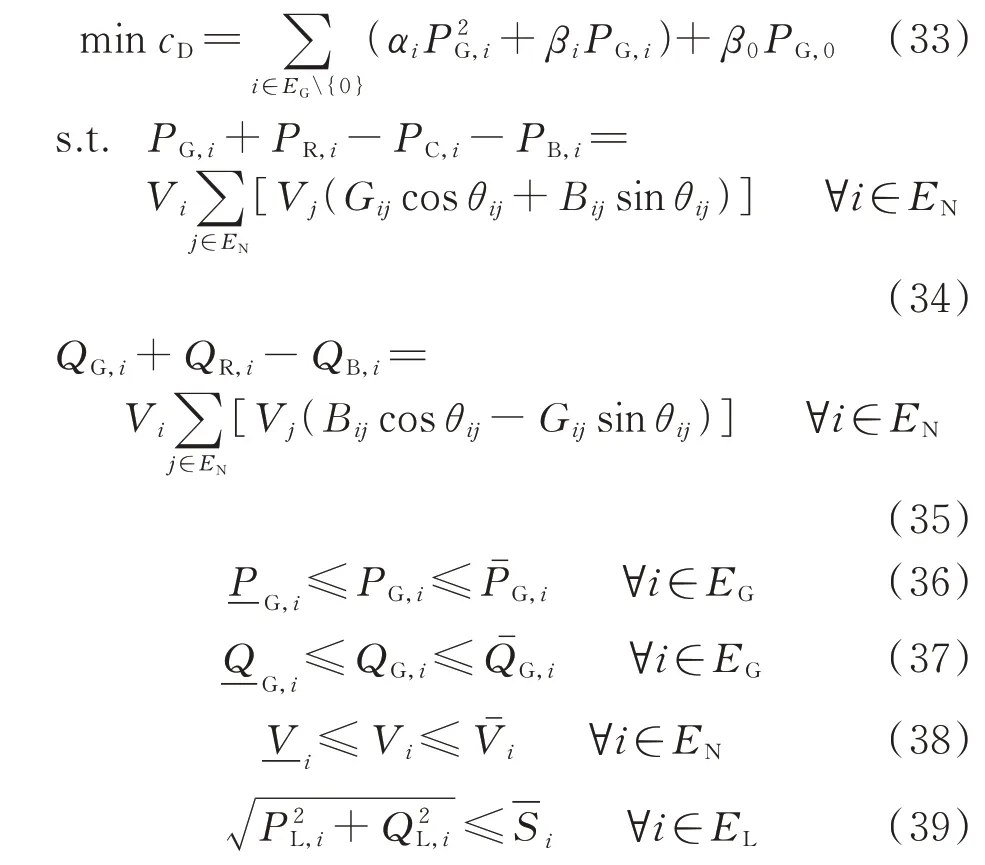
式中：cD为配电网的运行成本；αi和βi为分布式电源发电的成本系数；β0为配电网从上级电网购电的成本系数；PG，i和QG，i分别为节点i电源或平衡节点的有功和无功注入功率；PC，i为节点i充电站充电负荷有功功率；PL，i和QL，i分别为线路i的有功和无功传输功率；Vi为节点i的电压幅值；θij为节点i和节点j电压的相角差；Gij和Bij分别为配电网节点导纳矩阵第i行、第j列元素的实部和虚部；G，i、G，i和G，i、G，i分别为节点i电源或平衡节点有功和无功注入功率的下限、上限；和分别为节点i电压幅值的下限和上限；为线路i的最大传输功率。

上述模型的目标函数为配电网的运行成本。式（34）和式（35）为节点功率平衡约束；式（36）至式（39）分别为电源与平衡节点的有功和无功注入约束、节点电压幅值约束及线路传输功率约束。

本文采用交通网运行时段内充电负荷的平均功率作为配电网充电负荷的有功功率，且暂不考虑充电负荷的无功功率。其中，充电站s的充电负荷量Fs可在求解概率交通分配模型后求得：

本文以充电站所在节点边际电价作为充电站充电电价［7］，其可通过求解交流最优潮流模型中的拉格朗日对偶乘子得到。

3 考虑多重不确定性因素的交通网与配电网概率联合流计算

3.1 交通网与配电网耦合运行均衡状态分析

交通网与配电网协同运行中，基于充电站的充电负荷与充电电价耦合互动。在交通网与配电网的相互作用下，耦合系统会达到一个均衡状态。该均衡状态解的存在性与唯一性的证明并非本文关注的重点，具体可参见文献［6-8］。

本文采用分散迭代算法，通过迭代求解概率交通分配模型与配电网概率最优潮流模型，得到不确定性场景下耦合系统的均衡状态解，迭代求解过程如附录A 图A1 所示。给定随机场景(ξ，PD)，其中，ξ为交通网“路-车”不确定性因素，包括道路容量ξC、道路环境温度ξT、汽车出行需求ξN、电池初始SOC分类后的各类电动汽车数量占比ξS、电动汽车充电结束时的SOC 变量ξF；PD为配电网“源-荷”不确定性因素，包括可再生能源有功功率PR与除充电站充电负荷外其他负荷的有功功率PB。配电网侧充电站节点的电价λ会影响交通网汽车用户的出行成本cT，从而影响用户的充电决策与路径规划，并体现为交通流的变化；交通流的变化会通过映射η(fE)（即式（40））改变交通网充电站的充电负荷F，进而影响配电网潮流的分布，再经由映射π(PG)（即最优潮流模型的拉格朗日乘子提取）反馈为充电电价λ的调整，反过来影响交通网流量分布；通过不断交互迭代获得交通网与配电网耦合系统的均衡状态解，即随机场景(ξ，PD)下交通-电力联合流结果。

3.2 交通网与配电网概率联合流计算流程

为表征“路-车-源-荷”多重不确定性因素影响下交通网与配电网的联合流特征，建立交通网与配电网概率联合流计算模型：

式中：XT为求解交通分配模型所需的交通网数据；XD为求解配电网最优潮流模型所需的配电网数据；Y为交通网与配电网均衡状态下的耦合系统状态变量（如交通网的道路车流、出行成本，配电网的节点电压、线路功率等）；f(·)为求解交通网与配电网耦合运行均衡状态的映射关系（如3.1 节所示）。

上述模型中，系统的输入变量ξ、PD具有随机不确定性，考虑不确定性传播过程，系统的输出变量即交通网与配电网耦合系统状态变量Y也具有概率特性。本文通过蒙特卡洛模拟（MCS）方法，计算所有不确定性场景下的交通网与配电网联合流结果，并以所得交通流和电力流的概率分布量化表征不确定性因素对交通网与配电网耦合系统运行状态的影响。交通网与配电网概率联合流计算流程如下：

步骤1：获取交通网、配电网的基本信息，并选取交通网与配电网中的“路-车-源-荷”多重不确定性因素组成系统M维独立输入随机变量(ξ，PD)；

步骤2：基于统计数据，采用本文所提概率分布函数刻画交通网与配电网中的“路-车-源-荷”多重不确定性因素，建立输入变量(ξ，PD)的随机模型；

步骤3：基于所建立的输入随机变量模型，通过Sobol’序列采样或拉丁超立方采样等低差异序列采样方法［25］，得到J组输入随机变量样本(ξj，PD，j)（j=1，2，…，J）；

步骤4：基于大规模的输入随机变量样本，通过所提交通网与配电网耦合运行均衡状态求解方法，获得每组样本(ξj，PD，j)对应的交通网与配电网联合流输出变量样本Yj；

步骤5：计算输出变量样本Yj的统计特征量，如均值、方差、概率密度函数（PDF）、累积分布函数（CDF）等，作为交通网与配电网概率联合流计算结果。

4 基于全局灵敏度分析的交通网与配电网多重不确定性因素影响量化

交通网与配电网概率联合流计算结果从宏观上表征了“路-车-源-荷”多重不确定性因素对耦合系统运行状态的影响，然而，各个不确定性因素对交通流、电力流的影响程度并不相同，如何量化“路”“车”“源”“荷”各自对交通流、电力流的影响程度，以反映不确定性传播下耦合系统的交互影响是需要进一步解决的问题。灵敏度分析方法是量化输入变量影响程度的有效手段［26］，但交通网与配电网耦合系统内的不确定性传播过程并非瞬时完成，且概率联合流结果体现的是长时间尺度运行下不确定性因素的影响，这使得传统以偏导数为基础的局部灵敏度方法不能适用。因此，本文引入全局灵敏度分析方法，充分考虑长时间尺度下输入随机变量的概率分布特征，以实现交通网与配电网内“路-车-源-荷”多重不确定性因素的影响量化。

4.1 基于Sobol’法的全局灵敏度分析

全局灵敏度分析是一种量化输入随机变量影响的灵敏度分析手段，目前已用于含随机源-荷的电力系统潮流分析［27］、小干扰稳定分析［28］等。本文采用Sobol’法计算交通网与配电网多重不确定性因素的全局灵敏度指标，通过指标大小获得不确定性因素重要性排序，从而实现交通网与配电网耦合系统内不确定性因素的影响量化。

Sobol’法基于方差分析（ANOVA）理论，采用方差表征系统输入、输出变量的不确定性，并将系统输出变量的方差归因于各个输入变量及输入变量间的交互作用［29］。假设系统模型为Y=f(z)，其中，z=[z1，z2，…，zM]为M维独立输入随机变量。基于Sobol 分解理论，可对系统模型做如下分解：

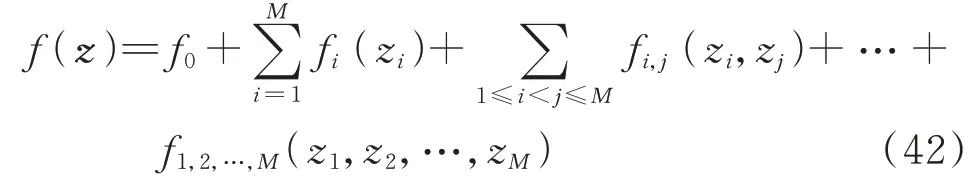
式 中 ：f0为 常 数 ；fi(zi)、fi，j(zi，zj)、f1，2，…，M(z1，z2，…，zM)为各分解子项函数。

若f(z)平方可积，且展开式中各子项均值为0，则各子项间两两相互正交，且各子项可唯一确定。将式（42）两边同时取方差可得：

其中

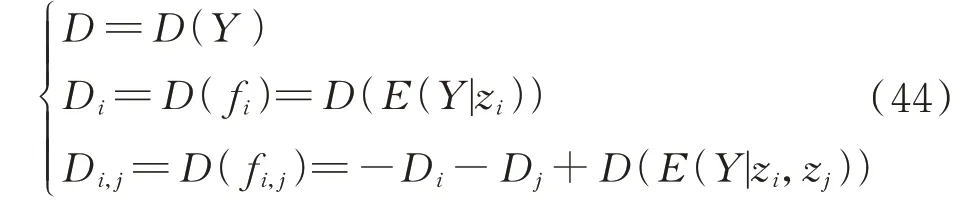
式中：E(Y|zi)为给定zi时Y的条件期望；E(Y|zi，zj)为给定zi与zj时Y的条件期望；D为输出变量的方差；Di为一阶偏方差，表示单一输入变量zi对输出变量方差的贡献程度；Di，j为二阶偏方差，表示输入变量zi与zj之间交互作用对输出变量方差的贡献程度。以此类推，其他各阶偏方差具有类似含义。输入变量zi的总偏方差DTi表示变量zi单独作用以及zi与其他输入变量交互作用对系统输出变量方差的共同贡献程度，如式（45）所示。

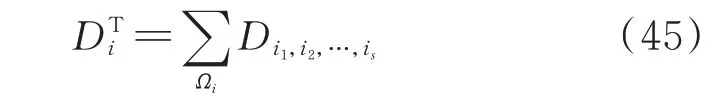
式中：Di1，i2，…，is为输入变量zi1，zi2，…，zis的s阶偏方差；Ωi={(i1，i2，…，is)：∃k，1 ≤k≤s，ik=i}。

定义标准化的全局灵敏度指标为：

式中：Si（1 ≤i≤M）为输入变量zi的一阶灵敏度指标（FSI），反映了单一输入随机变量zi对输出变量不确定性（方差）的影响；（1 ≤i≤M）为输入变量zi的总灵敏度指标（TSI），反映了输入变量zi单独作用以及zi与其他输入变量交互作用对系统输出变量不确定性（方差）的共同影响。

FSI 与TSI 的计算通常基于MCS 方法［26］，然而，大量反复的样本生成与模型求解使得该方法耗时严重。为了提高交通网与配电网多重不确定性因素影响量化过程的计算效率，本文引入稀疏多项式混沌展开（SPCE）代理模型以实现全局灵敏度指标快速计算。

将系统模型Y=f(z)表示为正交多项式的稀疏混沌展开如下：

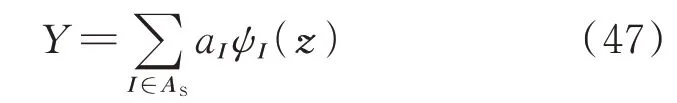
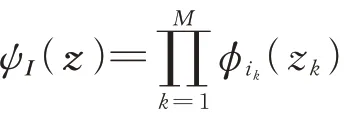
SPCE 代理模型的构建流程可参见文献［30］。当SPCE 代理模型确定后，利用展开式的各项系数即可计算得到系统输入随机变量的全局灵敏度指标。对于系统输入随机变量ξu（u=1，2，…，M），其FSI 与TSI 计算公式如下［31］：

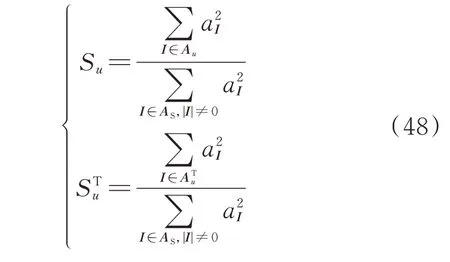
式中：Au={I∈AS：iu＞0；il=0，∀l∈{1，2，…，M}u}；={I∈AS：iu＞0}。

SPCE 代理模型的构建仅需少量系统输入-输出变量样本，因此，应用SPCE 代理模型计算全局灵敏度指标能够显著减少计算耗时，提高计算效率。

4.2 “路-车-源-荷”多重不确定性因素的影响量化

结合Sobol’法与SPCE 代理模型，计算交通网与配电网“路-车-源-荷”多重不确定性因素的全局灵敏度指标，以实现不确定性因素的影响量化。需要说明的是，本文侧重于量化耦合系统中不确定性因素对耦合系统状态变量的单独影响，因此，后续计算中仅采用了FSI 作为全局灵敏度指标对输入随机变量进行重要性排序，具体计算流程如下：

步骤1：基于MCS 方法获得少量交通网与配电网耦合系统输入-输出样本，用于SPCE 代理模型构建。该过程即为交通网与配电网概率联合流计算过程，具体步骤见3.2 节。

步骤2：基于Sobol’方法与代理模型，实现全局灵敏度指标的快速计算，具体计算如下。

1）设定步骤1 所生成的输入-输出变量样本规模为JS，通过累积分布函数变换建立输入变量样本(ξj，PD，j)（j=1，2，…，JS）与标准正态分布变量样本zj（j=1，2，…，JS）之间的转换关系，标准正态分布变量z与原输入随机变量(ξ，PD)的全局灵敏度指标分别对应。

2）选取SPCE 代理模型的基函数类型为Hermite 正交多项式，将标准正态分布变量样本zj作为代理模型输入变量样本，输出变量样本为Yj（j=1，2，…，JS），构建SPCE 代理模型。

3）利用SPCE 代理模型表达式，基于式（48）计算系统输入随机变量的FSI。

4）通过比较输入随机变量的全局灵敏度指标数值大小，获得交通网与配电网耦合系统不确定性因素的重要性排序，辨识对耦合系统具有显著影响的关键不确定性因素。

上述计算过程的流程图如附录A 图A2 所示。

5 算例仿真

5.1 算例系统

本文用于仿真测试的耦合系统A 由16 节点环形交通网与改进的IEEE 33 节点配电网构成；耦合系统B 由美国Sioux Falls 交通网与改进的IEEE 69节点配电网构成。耦合系统A、B 的拓扑图分别如附录B 图B1、图B2 所示。耦合系统A、B 的参数设置分别见附录C、附录D。基于文献［24］，本文假定风电机组、光伏电池的输出功率与风速、光照强度之间的关系如附录E 所示。本文仿真环境为Intel Core i7-10 700 8 核CPU、16 GB 内存，使用MATLAB R2020b 编译和测试。

5.2 交通网与配电网概率联合流计算

1）耦合系统A

考虑交通网与配电网中的“路-车-源-荷”多重不确定性因素，本文采用MCS 方法计算交通网与配电网的概率联合流，采样规模J=10 000。耦合系统A中所设置的系统输入随机变量为：5 个分布式可再生能源的输出功率PR，i（i=12，22，18，33，25）；4 个区域的道路容量随机波动ξC，i（i=1，2，3，4，分别对应工业区、休闲区、居民区、商业区），区域i内任意一条道路a的容量随机波动ξC，a均为ξC，i；起点分别为节点1、3、4 的O-D 对汽车出行需求量随机波动ξN，i（i=1，3，4），表示起点为i的任意O-D 对w间燃油汽车和电动汽车的出行需求量随机波动与均为ξN，i；起点分别为节点1、3、4 的电动汽车电池初始SOC 为0.3、0.6 的数量占比ξS，i，t（i=1，3，4；t= 1，2）（本算例将O-D 对起点处的电动汽车分为3 个类别，3 个类别内电动汽车的电池初始SOC 分别采用0.3、0.6、0.9 代替，起点为i的任意OD 对w间第t个类别的电动汽车数量占比ξS，w，t均为ξS，i，t，第3 类的电动汽车占比可由总比例1 减去另外2 类的占比之和得到）；电动汽车充电结束时的电池SOC 变量ξF；道路环境温度ξT，总的输入变量维度M=20。在计算交通网与配电网耦合运行均衡状态时，静态交通分配模型通过调用IPOPT 求解器求解，配电网交流最优潮流模型则借助Matpower 工具包求解。

根据所得耦合系统状态变量的统计结果，分别选取33 节点配电网各节点的电压幅值与16 节点交通网各道路的车流量作为概率联合流分析对象，绘制箱形图如图1（a）和（b）所示。由图1（a）可知，配电网各节点电压幅值分布范围均不一致，其中，节点17、18 的电压幅值分布最分散，其波动幅度较大且存在电压幅值较高的极端场景，相对其他节点具有较大的电压越限风险；节点24、25 的电压幅值较大概率位于0.95 p.u.以下，是配电网中电压薄弱的环节，也存在一定的安全风险。由图1（b）可知，交通网各道路车流量的分布范围差异明显，道路1→13、3→14 的平均车流量及其波动幅度显著高于其他道路，极端场景下其车流量最大分别可达2 248 辆/h与2 276 辆/h，在道路可用容量意外减小时（如交通事故、道路维护等）更容易发生瞬时车流量过大而导致的交通堵塞现象。因此，在道路扩建规划时，也需优先考虑上述道路。

图1 交通网与配电网耦合系统A 状态变量的箱形图Fig.1 Box plots of state variables in coupled system A of transportation network and distribution network

对于33 节点配电网，分别计算节点8 电压幅值（V8）、充电站4 充电电价（λ4）的PDF 如图2（a）、（b）所示；对于16 节点交通网，分别计算交通网中道路8 →9 车流量（x8→9）、充电站4 充电负荷（F4）的PDF如图2（c）、（d）所示。对比图2 中的结果可知，充电站4 节点电价的PDF 具有双峰分布的特点，其在交通网与配电网耦合交互过程中，容易受到多重不确定性因素的影响；由图2（c）可知，道路8→9 的车流量存在超过道路预警容量的风险（本文以道路容量基准值加上随机波动标准差的3 倍设定为道路预警容量），基于道路8→9 车流量的PDF 能够计算得到其越限概率（即车流量超过道路预警容量的概率）为28.22%。

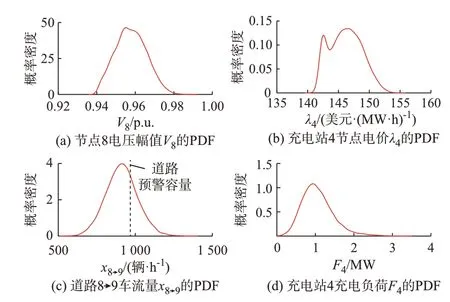
图2 交通网与配电网耦合系统A 状态变量的PDFFig.2 PDF of state variables in coupled system A of transportation network and distribution network

2）耦合系统B

对于耦合系统B，分别选取69 节点配电网中节点56 的电压幅值（V56）与Sioux Falls 交通网中道路12 的车流量（x12）作为分析对象，计算其PDF 如附录F 图F1 所示。根据耦合系统B 的概率联合流计算结果，得到Sioux Falls 交通网道路车流量均值与越限概率热力图如图3（a）、（b）所示。由图3（a）可知，仅有少量道路的车流量均值显著大于其他道路；由图3（b）可知，部分道路的车流量越限概率较高，容易发生交通堵塞现象。结合图3（a）、（b）可知，部分道路由于容量偏小，在车流量不大的情况下也存在较高的交通堵塞风险。为了改善该交通网的通行能力，需要对上述道路进行合理扩建或增强与电网的联合调控。基于上述结果可知，对于较大规模的交通网与配电网耦合系统，本文所提概率联合流计算方法仍具有适用性。

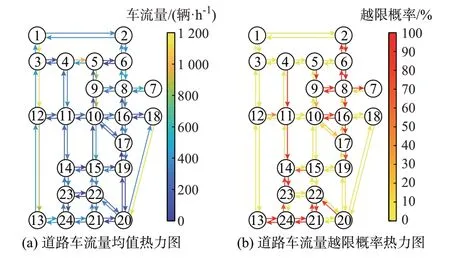
图3 Sioux Falls 交通网道路车流量均值与越限概率热力图Fig.3 Heat maps of traffic flow mean value and limit violation probability of road in Sioux Falls transportation network

综合耦合系统A、B 的概率联合流计算结果可知，由于交通网与配电网内“路-车-源-荷”多重不确定性因素的影响，通过不确定性传播过程，系统的输出变量（即交通网与配电网耦合系统状态变量）也具有概率特性。同时，通过计算交通网与配电网的概率联合流结果，系统运行者能够获得系统各状态变量的概率统计信息，从而为交通网、配电网的联合运行分析、运行状态感知与预警提供更全面的信息参考。

5.3 交通网与配电网多重不确定性因素影响量化

在交通网与配电网概率联合流计算的基础上，利用基于Sobol’法的全局灵敏度分析方法，量化交通网与配电网中“路-车-源-荷”多重不确定性因素的影响，辨识显著影响交通网与配电网耦合运行的关键不确定性因素。本文利用UQLab［32］构建交通网与配电网联合流的SPCE 代理模型，实现全局灵敏度指标的快速计算。

1）耦合系统A

首先，为了验证基于SPCE 代理模型的全局灵敏度指标计算方法的有效性，将所提方法与传统的MCS 方法进行对比分析。考虑耦合系统A 中的20 个系统输入随机变量，以V8作为输出变量，分别计算各个系统输入随机变量的FSI。SPCE 代理模型的最高阶数为10，模型构建所用的样本规模JS=600；MCS 方法的采样规模为10 000。任意选取5 个系统输入随机变量：WT1 的输出功率（PR，12）、区域1 道路的容量随机波动（ξC，1）、起点为节点1 的O-D 对汽车出行需求量随机波动（ξN，1）、起点为节点1 的电动汽车电池初始SOC 为0.3 的数量占比（ξS，1，1）、电动汽车电池充电结束时的SOC（ξF）。通过SPCE 代理模型与MCS 方法分别计算得到FSI结果与计算用时如表1 所示。

表1 SPCE 代理模型与MCS 方法的FSI 计算结果对比Table 1 Comparison of FSI calculation results between SPCE agent model and MCS method

由表1 可知，通过SPCE 代理模型计算得到的FSI 结果与MCS 方法基本一致，其平均数值误差为0.004 6。同时，通过SPCE 代理模型计算FSI 能够大幅减少计算用时（由MCS 方法的191.2 h 减少至2.3 h）。因此，基于SPCE 代理模型的全局灵敏度指标计算方法能够在保证计算精度的前提下，显著提高计算效率。

对于33 节点配电网，以节点8 电压幅值（V8）为输出变量，通过基于SPCE 代理模型的全局灵敏度指标计算方法，得到20 个系统输入随机变量的FSI如附录F 图F2（a）所示；对于16 节点交通网，以道路8→9 车流量（x8→9）为输出变量，计算得到20 个系统输入随机变量的FSI 如图F2（b）所示。

由附录F 图F2 可知，仅有少量系统输入随机变量的FSI 数值结果较大，说明并非所有系统输入变量的随机性对系统输出都有显著影响。以FSI 计算数值结果较大的系统输入随机变量作为关键输入变量，则对于输出变量V8影响最显著的关键输入变量为WT1、WT2 的输出功率（PR，12、PR，22）及起点为节点1 的电动汽车电池初始SOC 为0.3 的数量占比（ξS，1，1）；对于输出变量x8→9影响最显著的关键输入变量为区域1 道路的容量波动（ξC，1）及起点为节点3、4 的O-D 对汽车出行需求量随机波动（ξN，3、ξN，4）。可以看到，在本文所设置的参数条件下，交通网中的“路-车”不确定性因素对配电网状态变量的影响相较于配电网中的“源-荷”不确定性因素对交通网状态变量的影响更为显著。

进一步，为了验证所提交通网与配电网多重不确定性因素影响量化方法在辨识关键输入随机变量方面的有效性，本文以V8为输出变量设置如下3 种场景：

场景1：考虑所有20 个输入变量的随机性；

场景2：仅考虑3 个关键输入变量的随机性，其余非关键输入变量取固定值；

场景3：仅考虑其余非关键输入变量的随机性，3 个关键输入变量取固定值。

基于交通网与配电网概率联合流计算，可分别得到3 个场景下V8的CDF 如图4 所示。

图4 不同场景下V8的CDFFig.4 CDF of V8 in different cases

由图4 可知，仅考虑3 个关键输入变量的随机性时（场景2），输出变量V8的CDF 与考虑所有20 个输入变量随机性时（场景1）基本一致；反之，当3 个关键输入变量取固定值，仅考虑其余输入变量随机性时（场景3），输出变量V8的CDF 与场景1 有很大差异。算例结果表明，全局灵敏度指标所辨识的关键输入变量对输出变量具有显著影响，关键输入变量的随机性是输出变量随机性的主要来源，进一步，验证了本文所提交通网与配电网多重不确定性因素影响量化方法在辨识关键不确定性因素方面的有效性。

2）耦合系统B

对于耦合系统B，分别选取69 节点配电网中节点56 的电压幅值（V56）与Sioux Falls 交通网中道路12 的车流量（x12）作为输出变量，计算系统随机输入变量的FSI。取FSI 指标排序前5 的系统输入随机变量作为关键随机变量，计算结果如附录F 表F1 所示。由表F1 可知，对于输出变量V56影响最显著的关键输入变量为位于节点12、51、52、58、59 的可再生能源输出功率，对于输出变量x12影响最显著的关键输入变量为工业区2 道路的容量波动及起点为节点1、2、4、9 的O-D 对汽车出行需求量随机波动。

6 结语

本文考虑“路-车-源-荷”多重不确定性因素，建立了交通网与配电网概率联合流计算模型，并引入了基于SPCE 代理模型的全局灵敏度分析方法，量化多重不确定性因素对交通网与配电网耦合运行的影响。主要结论如下：

1）考虑“路-车-源-荷”多重不确定性因素的概率联合流计算模型能够量化表征交通网与配电网耦合运行的联合流概率特性，为交通网、配电网的联合运行分析、运行状态感知与预警提供更全面的信息参考。

2）基于SPCE 代理模型的全局灵敏度分析方法能够准确、高效地量化“路-车-源-荷”多重不确定性因素对交通网与配电网耦合运行的影响程度，辨识关键不确定性因素，为耦合系统不确定性分析中随机变量的降维提供方法支撑。

下一步工作是研究汽车用户成本认知水平差异、用户行为的随机-模糊特征对交通网与配电网概率联合流的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。