基于深度学习考虑出行模式的电动汽车充电负荷场景生成
钱 涛,任孟极,邵成成,朱丹丹,周 前,王秀丽
(1. 西安交通大学电气工程学院,陕西省西安市 710049;2. 国网江苏省电力有限公司电力科学研究院,江苏省南京市 211103)
0 引言
随着电动汽车的发展和普及,交通用能正逐步由油气转变为电能[1-2]。中国城市人口稠密,快速充电站是提供集中、便捷充电服务的必然选择。随着“新基建”的开展,中国充电设施发展迅猛:2020 年充电桩数量增长了35.4%,达165.1 万个。作为交通网与电网耦合的纽带,快速充电站的充电负荷受电动汽车交通出行模式影响深刻[3],对电网运行提出了新的要求。电动汽车快速充电站负荷模拟已成为未来电网规划与运行的重要基础。
近年来,各国学者对于电动汽车充电负荷模拟[4-9]做了大量的研究工作。文献[4]采用蒙特卡洛模拟的方法,预测了电动汽车充电负荷的时空特性。文献[5]建立基于经验模态分解-模糊熵和集成学习的电动汽车充电需求预测方法,对受天气影响的充电负荷进行了预测。文献[6]通过对电动汽车聚集商的建模,描述了电动汽车群体充电负荷的分布,为电网运行决策提供了支撑。文献[7]建立了电动汽车交通均衡的模型,并设计了可行路径迭代算法对模型进行求解,揭示了交通网侧的信息对电动汽车充电负荷的影响。文献[8]分别从电动汽车用户社会行为分析和选择充电的灵活性入手,模拟了不同时间段内的电动汽车充电负荷。文献[9]建立了多类别混合与指派模型,描述了充电站位置分布等信息对充电负荷的影响。然而这些方法主要基于对交通网乃至电动汽车用户的个体建模,不仅要求获知如道路通行能力等交通网参数,还需要对交通参与者的行为模式进行量度。这些要求使电网运行人员对充电站充电负荷的分析较为困难。本文提出一种基于数据驱动的电动汽车充电站充电负荷场景生成方法,不依赖于对交通路网及其参与者行为的建模,方便高效地为电网运行与规划提供支撑。
对抗生成网络(GAN)是一种基于深度学习的生成模型,具有良好的自适应性和泛化能力,近年来在电力系统领域的应用也引起了广泛的关注。文献[10]采用改进辅助分类GAN 提升了高噪声环境下基于非平衡振动数据的风机主轴承故障诊断的准确率。文献[11]利用GAN 模拟风光出力场景,为微网电源容量最优配置提供了支撑。文献[12]根据改进的GAN,解决了自能源中电-气-热数据时间异步问题,并实现了能源设备的分类和辨识。文献[13]采用条件对抗生成网络(CGAN)研究了新能源出力日前场景生成问题,为电网运行提供了支撑。文献[14]探讨了GAN 在暂态稳定预防控制和动态安全评估方面的作用。但是GAN 的训练面临一定困难,特别是CGAN,当条件信息较为复杂时难以有效得出给定条件下的隐式概率分布信息。
本文提出了一种基于数据驱动的电动汽车充电站负荷场景生成方法,不依赖交通网与参与者的具体参数,为电网和充电站的规划运行提供参考。考虑不同交通出行模式对快速充电站充电负荷的显著影响,采用了基于深度学习的CGAN,隐式地学习出不同模式下充电负荷条件概率分布。针对CGAN 在复杂条件下训练困难的问题,提出了基于无监督学习的卷积自编码器方法,并采用了更为有效的基于软间隔支撑向量机(SVM)的损失函数,显著提升了CGAN生成充电负荷场景的效果。
1 充电负荷场景生成的问题描述
不同的交通模式会在时间和空间上显著影响公共充电站的充电负荷分布。例如,早高峰、晚高峰的出行模式与正常时段会有明显的差别。本文考虑在高比例电动汽车接入的场景下,电网运行人员需要在日前对第2 天电动汽车充电负荷进行评估,首先从交通部门获得预测的交通模式数据,然后再根据预测的交通模式数据生成第2 天的电动汽车充电负荷场景,为电网的运行决策提供支撑。
不少已有研究通过OD(origin-destination)矩阵描述交通出行模式,然而在实际中OD 矩阵数据统计困难。本文将交通模式简化定义为各时段从交通网各节点出发的电动汽车数量,构成交通出行模式矩阵M:
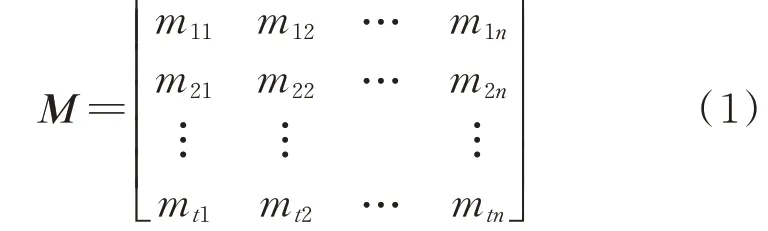
式中:mtn为t时刻从交通网节点n出发的电动汽车的流量。可见,M的行和列分别代表了空间与时间的相关关系,这与深度学习研究中的图像识别问题有密切联系,也是本文采用卷积神经网络的原因。
从电网运行出发,电动汽车充电负荷模拟的目的是根据预测的电动汽车交通出行模式矩阵M得到各充电站各时段的充电站充电负荷矩阵Y:

式中:yts为t时刻充电站s的充电负荷。
考虑到交通出行模式矩阵M的预测误差以及电动汽车用户行为、路况等的随机性,充电负荷并非交通模式预测值的确定性函数,而是应服从以其为条件的概率分布。换言之,从电网运行人员的角度出发,第2 天的充电负荷具有随机性,假设服从未知的概率分布P(Y),其中Y包含了充电负荷数据。这个概率分布受到很多交通因素的影响。本文讨论如何在已知交通模式预测数据的条件下,通过数据驱动的方法隐式地学习得出充电负荷的条件概率,如式(3)所示,其中M包含了交通模式预测数据。

本文根据数据驱动的思想,采用了基于CGAN的深度学习方法,根据交通模式预测数据-充电站负荷数据集,隐式地学习得出该条件概率分布,从而依据预测的交通出行模式矩阵估计各充电站各时段的充电负荷。
2 充电负荷场景的生成方法
本文首先通过卷积自编码器对交通出行模式矩阵进行降维,抽取出特征信息,再训练CGAN 生成不同交通模式下的电动汽车充电负荷场景。
2.1 卷积自编码器
为提取出交通出行模式矩阵M的特征信息,类比图像识别问题,本文采用了卷积自编码器。它主要由卷积编码器和转置卷积解码器两个部分构成。卷积神经层将高维的输入矩阵通过卷积操作实现下采样,提取一定范围内的数据特征,得到降维后的输出矩阵。经过多层卷积神经层的操作,最终可以得到包含全局信息且维数降低的特征信息。与之相对应,转置卷积神经层则将低维的输入矩阵通过转置卷积实现上采样,还原输入矩阵的原始信息。如果将神经层的运算写成矩阵算子,则在算子维数上,卷积操作和转置卷积操作互为转置:

式中:X为高维输入矩阵展平形成的向量;Z为低维的特征矩阵;A为卷积算子;BT为转置卷积算子。A与BT在维数上存在转置关系。
基于上述卷积与转置卷积神经层,可构造如附录A 图A1 所示的卷积自编码器。卷积自编码器是一种基于无监督学习的算法,利用卷积和转置卷积神经网络的深层结构来重建其输入矩阵。具体地,输入矩阵首先经过卷积编码器压缩为一个低维的特征矩阵,然后再由转置卷积解码器重建原始输入矩阵,以实现对输入数据降维并提取特征信息的目的。训练过程的目标是最小化原始输入数据和重建输出数据之间的距离,其训练的目标函数可以表示为:
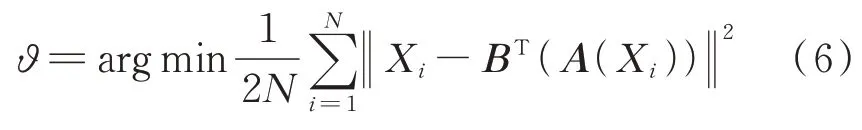
式中:Xi为第i个训练数据。训练完成后,经过卷积编码器即可得到原始交通出行模式矩阵降维后的特征矩阵。
2.2 条件对抗生成网络
GAN 是一种利用博弈对抗思想从历史数据中隐式学习其概率分布的方法,如图1 所示。通过交替地训练生成器和判别器,最终达到将噪声转化成与历史数据相近的概率分布的效果。CGAN 在GAN 基础上更进一步[15],可根据给定的不同条件信息将噪声映射为不同的条件概率分布,对来自多分布的数据具有良好的生成能力。
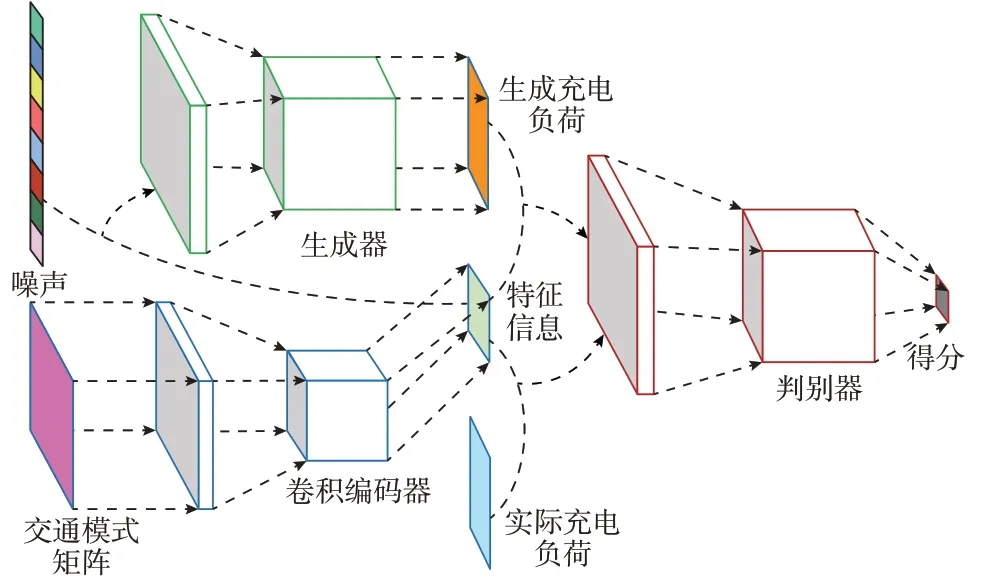
图1 CGAN 训练过程示意图Fig.1 Schematic diagram of CGAN training process
首先,将交通出行模式矩阵M输入训练好的卷积编码器,降维得到特征信息矩阵。将特征信息矩阵展平为向量,与从正态分布中抽取得到的噪声一起输入由卷积神经层组成的生成器,生成充电负荷矩阵。判别器以充电负荷矩阵与特征矩阵堆叠而成的张量为输入,经由卷积神经层获得最终的标量得分。判别器的训练目标为将包含生成的充电负荷的张量和包含真实的充电负荷的张量分开,而生成器的训练目标为最大限度地使判别器无法正确地分类从而得到逼近真实数据潜在的概率分布。据此,训练CGAN 的目标函数可以表示为:
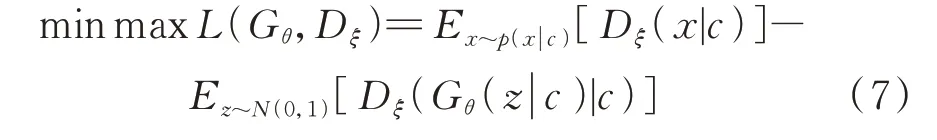
式中:L(Gθ,Dξ)为CGAN对于样本的损失得分;E为求期望;Dξ(·)为判别器;Gθ(·)为生成器;p(x|c)为给定类别信息c时的条件概率分布,x为从p(x|c)抽样产生的样本;z为从标准正态分布中抽样得到的噪声。在训练生成器时,将判别器固定,调整生成器的参数θ,最大化判别器对生成器生成样本的输出的得分。类似地,在训练判别器时,将生成器的参数固定,调整判别器的参数ξ,使得来自实际数据的样本得分尽量高,而来自生成器的样本得分尽量低,从而将其分类。
GAN 的训练较为困难,这是因为训练过程中很容易出现模式崩溃问题。 不少文献利用Wasserstein 距离作为判别器损失函数,能有效地表示出两个概率分布的距离。但CGAN 训练过程中常常面临“高维度小样本”的问题,即一批训练样本的数量要小于单个样本的维数,以Wasserstein 距离作为损失函数会使得学习的概率分布倾向于各条件概率分布的平均值[16],难以较好地逼近多个潜在的条件概率分布起。受soft-margin SVM 启发,可将生成样本和实际样本分类问题写成如下的优化问题:
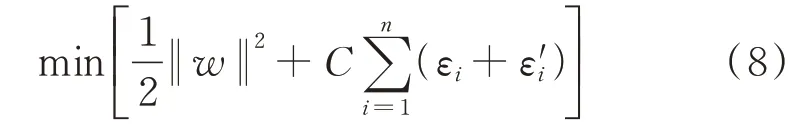
约束条件为:
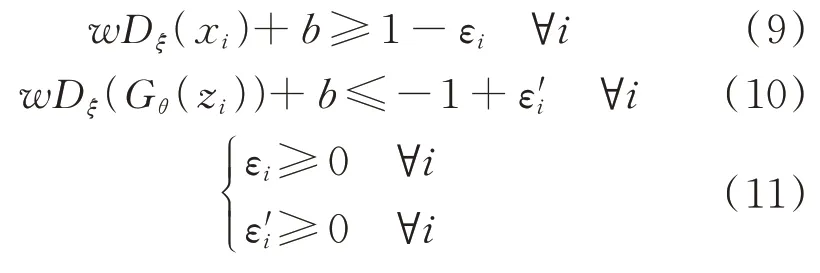
式中:w和b为分类直线的参数;εi和ε′i为软间隔的松弛变量;n为训练样本总数;xi和zi分别为第i个样本和抽样得到的噪声;C为权重系数。
上述优化问题的最优解能最大限度地将生成器产生样本和实际样本分隔在间隔两侧。根据SVM的理论,最优解w*可写成样本得分的线性组合,即

式中:λi和μi分别为约束式(9)和式(10)的对偶乘子,且仅当对应的εi和ε′i非零时不为零。此时对应的样本处于间隔中。那么可将优化问题式(8)的目标函数写为:
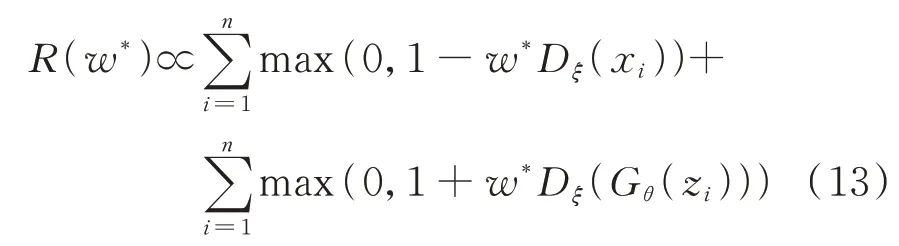
对应式(12),应当调整判别器参数使式(13)所示目标函数值最小,同时调整生成器参数使得样本的得分落在真实样本的同侧,如下文算例分析结果所示。判别器和生成器参数的梯度可以分别写作:
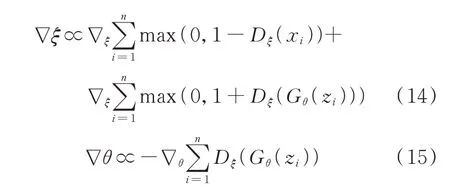
2.3 充电负荷场景生成流程
根据上文的网络结构和参数更新策略,可以得到充电负荷场景生成算法训练流程,如图2 所示。
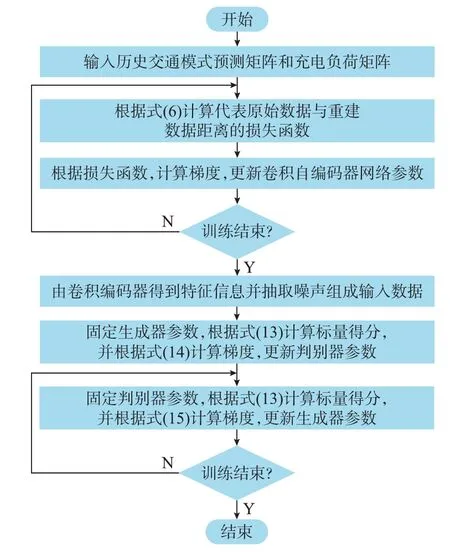
图2 充电负荷生成方法训练流程图Fig.2 Flow chart of training of charging load generation method
首先,利用交通出行模式历史数据矩阵训练卷积自编码器,根据式(6)计算损失函数,更新卷积编码器参数,完成训练后得到降维后的特征信息;再根据从标准正态分布中抽样得到的噪声组成生成器的输入数据。然后将生成器的参数固定,根据式(13)计算目标函数,再根据式(14)更新判别器参数以最大程度地区分真实充电负荷数据和由生成器模拟的充电负荷数据。其次,固定判别器参数,根据式(13)计算目标函数,再根据式(15)更新生成器参数,通过提高生成数据在判别器中的得分,使其逼近真实充电负荷数据服从的条件概率分布。在训练完成后,将判别器移除,即可由新的交通出行模式数据,经过卷积编码器和生成器,产生对应的充电负荷场景。
本文所采用数据驱动的方法旨在探讨交通出行模式与充电负荷“端到端”的对应关系。值得注意的是,充电站的地理相对位置与彼此之间交通网络信息会对充电负荷产生影响。应当指出:1)充电站位置、交通网络布局主要由规划方案决定,规划、建设方案确定后一般不发生改变;2)充电负荷除受充电站位置、交通网络布局等规划因素影响外,还与不同时刻的交通出行需求等运行因素密切相关;3)充电站位置、交通网络布局等规划因素会对城市中电动汽车交通流量的分布产生影响。因此,本文采用数据分析方法研究交通出行模式(即不同时间、不同节点出行需求)与充电负荷间“端到端”的对应关系。该研究以给定的交通网络拓扑为前提,对随交通出行需求变化的电动汽车充电负荷进行分析。应当指出,本文所提出的方法存在局限性。首先,本文方法未对交通网拓扑信息直接建模和表征,未考虑交通网拓扑发生变化时充电站充电负荷的变化特点。其次,本文方法重点关注和刻画了以城市公共充电站为耦合点的电网络和交通网络的耦合关系,未涉及社区充电桩等其他耦合形式的充电负荷场景生成。
3 算例分析
由于电动汽车正处于大规模推广的阶段,目前在汽车总量的占比依然较小。以中国西安市为例,2020 年机动车总量为370 万辆,而电动汽车为10.5万辆,占比2.83%,因此目前难以获得可以较好地反映高比例电动汽车下交通出行模式与充电负荷分布关系的实际数据。本文首先考虑采用文献[9]中的多类别混合与指派模型的模拟方法产生该类数据。该模型描述了稳态下交通网车流的均衡状态。在该交通均衡下,没有任何一辆车可以单方面地改变行驶路线,使得自己的行驶时间减小。这是对实际交通情况的一般性规律的建模和近似,在已有的研究中被广泛验证和应用[17-18]。
本文以西安市主城区交通路网为例进行分析,一共39 个节点、132 条道路[19],设有6 个大型的充电站,如附录A 图A3 所示。算例中2、3、7、8、12、15、18、20、21、30、33、35、36、37、38 共计15 个节点作为电动汽车出发点,并通过多类别混合与指派模型[9]模拟各充电站充电负荷。为反映不同交通出行模式的影响,首先将出发节点分成3 组(2,3,7,8,12)、(15,18,20,21,30)和(33,35,36,37,38),然后将电动汽车出行的模式归类分为“早高峰”“午高峰”和“晚高峰”,即从节点出发的电动汽车数量分别在早上、中午和晚上达到全天的最大值,如附录A 图A4所示。其次,将3 类出行模式随机地分配给3 组节点,最终得到6 种不同的整体交通出行场景。
针对交通出行数据随机性的特点,在模拟充电负荷时,流程如下:首先,根据以节点分配到的出行模式的典型曲线为均值的正态分布,抽样得到该节点的真实出行模式数据;其次,再以抽样得到的真实数据为均值,从新的正态分布中抽样得到交通出行模式的预测值。同时,根据第1 次抽样得到的真实出行模式数据,由文献[9]的模型模拟得到第2 天真实的充电负荷。在实际训练神经网络时,CGAN 所能接触到的只有第2 次抽样得到的交通出行模式的预测数据和由真实数据模拟得到的实际充电负荷,而无法获得第1 次抽样得到的交通出行模式实际数据。由此,最终可以根据训练得到的CGAN,由交通模式的预测值直接生成第2 天的充电负荷场景。
以西安市主城区交通路网为例,共考虑15 个电动汽车出发节点,24 个时段,那么矩阵的维数即为24 行、15 列。如此,一共随机生成了360 天的交通模式数据,组成了360×24×15 的张量,形成了模拟电动汽车充电负荷的交通模式输入数据。将交通模式数据和模拟得到的充电负荷数据组合在一起就得到了用来训练CGAN 的历史数据。值得注意的是,在训练CGAN 时,真实的交通出行数据是未知的,仅有预测的交通出行数据和由真实数据模拟得到的充电负荷数据作为训练的历史数据。本文所用到的卷积自编码器和CGAN 的详细参数见附录A。
3.1 训练过程
首先对卷积自编码器进行训练,如附录A 图A5所示。训练的损失函数值一开始处在较高水平,这说明此时卷积自编码器没有学习得出交通模式的特征信息。随着训练次数的增加,损失函数值快速降低并收敛,卷积自编码器已能较好地实现交通模式数据降维并抽取特征信息。6 种不同交通模式的特征信息等高线图如附录A 图A6 所示。原始的交通出行模式矩阵维度为24×15,而降维后特征信息维度为3×3。下节中将进一步说明卷积自编码器在充电负荷场景生成中的有效性和必要性。
CGAN 训练过程如附录A 图A7 所示。为取得更好效果,采取生成器、判别器异步训练的方法:判别器每训练4 步,生成器训练1 步。这使得在训练开始阶段,判别器可以非常准确地分辨真实数据和来自生成器的数据,判别器的损失函数接近0,生成器的损失函数较大。随着训练次数的增加,生成器可以较好地逼近真实数据服从的条件概率分布,这使其自身的损失函数显著减小,而判别器损失函数增加,两者博弈最终达到均衡状态。
3.2 方法对比
为了进一步说明本文方法的有效性,对如下4 种方法生成的充电负荷场景进行对比:1)由真实交通模式数据模拟得到的充电负荷场景;2)本文所提方法生成;3)由未使用卷积自编码器降维的CGAN 生成;4)降维但采用Wasserstein 距离作为损失函数的CGAN 生成。
利用4 种方法分别生成100 天的充电负荷场景,其总体分布情况如图3 所示,图中IQR 为四分位数间距。
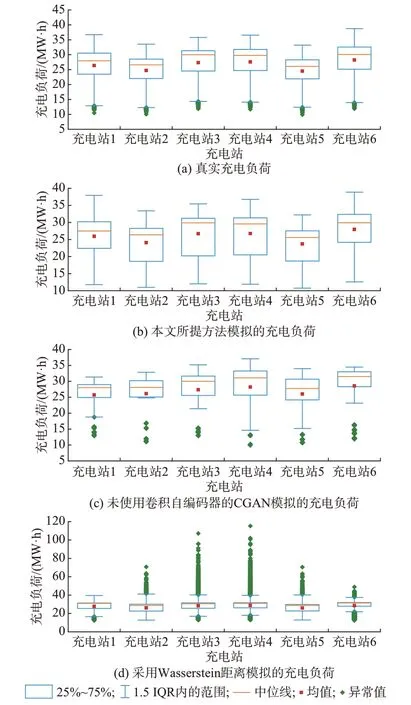
图3 不同方法生成各充电站的充电负荷箱形图Fig.3 Box plots of charging load of each charging station generated by different methods
可以发现,本文所提出的方法最接近真实的充电负荷分布,而未使用卷积自编码器的CGAN 只能在大致范围上近似真实分布,比如充电站1 和充电站2 充电负荷的均值和中位数的相对关系。而使用Wasserstein 距离作为CGAN 损失函数的方法没有能逼近真实的充电负荷分布,并且产生了较多的异常值。
对比后3 种方法生成负荷与真实充电负荷的相关系数,结果如表1 所示。本文所提出方法在5 个充电站中都有最接近1.0 的相关系数,并有最小的均方差。这说明本文所提出方法比对照方法更有效地反映充电负荷的时序特征。
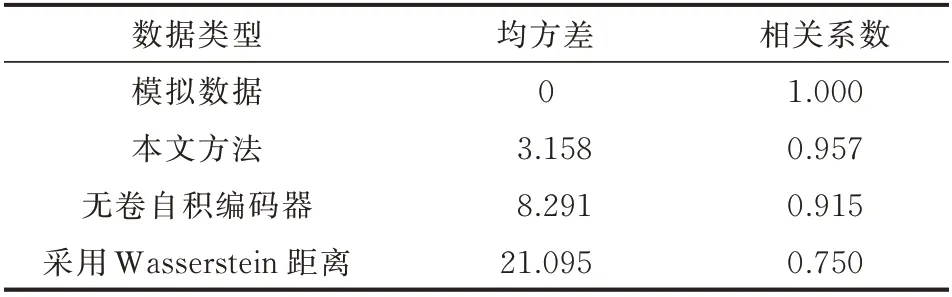
表1 不同方法生成负荷与模拟数据的评价指标比较Table 1 Comparison of evaluation indices between loads generated by different methods and simulated data
为进一步说明该问题,采用4 种方法生成72 h充电负荷场景,如附录A 图A8 所示。可以看出,在图A8(a)所示真实的充电负荷中,充电站1 与2、3 与4、5 与6 的充电负荷在时序上具有相似性。具体地,充电站1 和2 的充电负荷变化模式为早高峰-午高峰-晚高峰;充电站3 和4 的变化模式为午高峰-晚高峰-早高峰;而充电站5 和6 的变化模式为晚高峰-早高峰-午高峰。而本文所提出的方法,如图A8(b)中所示,可以有效地还原充电负荷的时序变化,与真实数据接近。而其他2 种方法未能学习出充电负荷的时序变化,其72 h 的充电负荷场景为同一模式。这说明卷积自编码器和基于软间隔SVM 目标函数可以显著地提升充电负荷模拟效果。值得注意的是,利用多类别混合与指派模型模拟的100 d 真实充电负荷用时208 min,而由本文提出方法生成100 d 的充电负荷场景用时0.63 s,在实际应用层面具有较大的潜力和良好的应用前景。
3.3 基于网约车历史轨迹的实际算例分析
为了检验所提出的方法在实际应用中的适用性,本文进一步分析了滴滴盖亚数据开放计划[20]中2016 年10 月西安主城区网约车订单历史轨迹数据集。接下来的算例分析假定这些网约车均为电动汽车。该脱敏数据集涵盖了170 530 位司机(人次)的全天订单时间空间信息。具体地,每条数据包括:司机脱敏编号、订单脱敏编号、经纬度和时间戳,详细地描绘了网约车司机在西安市主城区的时空轨迹。为了方便统计网约车的充电位置和计算充电负荷,本文将西安市主城区均匀地分为16 个区域,如附录A 图A9 所示。首先统计了每个区域每小时出发车辆的数量,形成了交通出行模式矩阵。其次,根据这些信息,逐车逐订单地计算了网约车行驶过程中的消耗电量与剩余电量,并得到了对应的西安市24 h各区域的充电负荷。具体步骤如图4 所示。
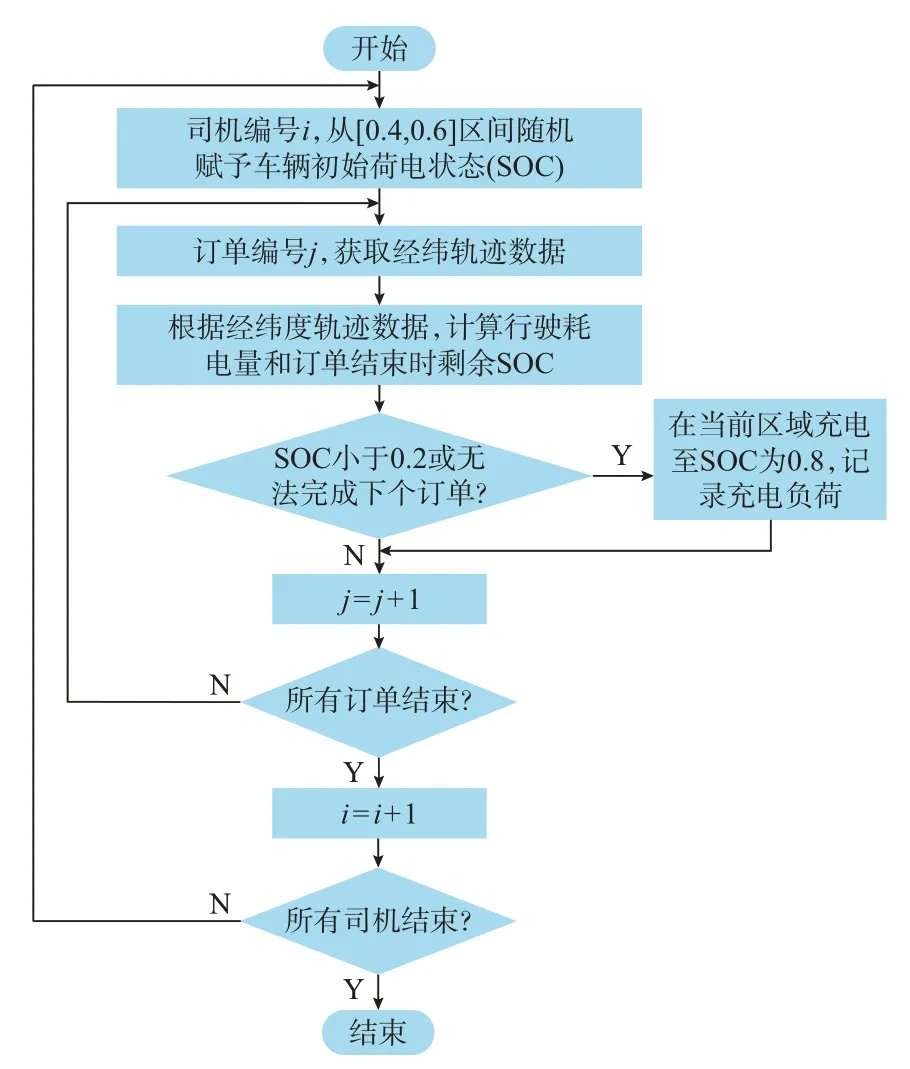
图4 实际算例充电负荷计算方法训练流程图Fig.4 Flow chart of training of charging load calculation method for actual example
计算完成后,共得到了30 组交通出行模式矩阵-充电负荷场景数据对。选取前20 组数据训练本文提出的卷积自编码器和CGAN,并选取后10 组作为测试数据,计算实际充电负荷与CGAN 生成的充电负荷之间的均方差和相关系数,如表2 所示。
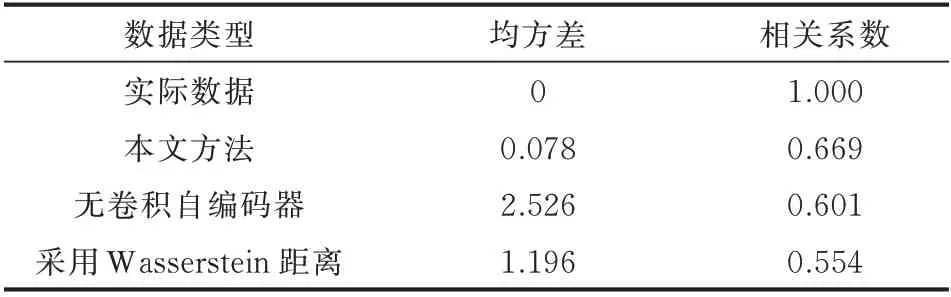
表2 不同方法生成负荷与实际数据的评价指标比较Table 2 Comparison of evaluation indices between loads generated by different methods and actual data
对比不同方法可以发现,本文所提出的方法与其他方法相比,显著减小了与实际数据的均方差,并有最高的相关系数,这说明其能更好地反映各区域充电负荷的不同模式。为了进一步阐述这一点,本文分析了不同算法生成的西安市各区域充电负荷的分布图,如图5 所示。
可以看出,图5(b)展示的本文方法生成的各区域充电负荷与图5(a)表示的实际充电负荷分布最为接近。图5(c)和图5(d)分别代表未使用卷积编自码器降维的CGAN 生成的充电负荷场景和使用Wasserstein 距离作为损失函数的CGAN 的充电负荷场景,可以看到,两种算法均会生成较多的异常值,难以在实际场景中应用。最后,图5(e)展示了利用文献[9]中的模型,模拟得到的各区域的充电负荷分布。可以发现,由于在实际算例中无法准确获取反映电动汽车用户行为偏好的参数,文献[9]模型的各区域充电负荷模拟结果趋近平均分布,与图5(a)的实际数据有较大的误差。综上,本文所提出的数据驱动的充电负荷场景生成方法在实际算例上有较好的效果,具有显著的实际应用潜力。
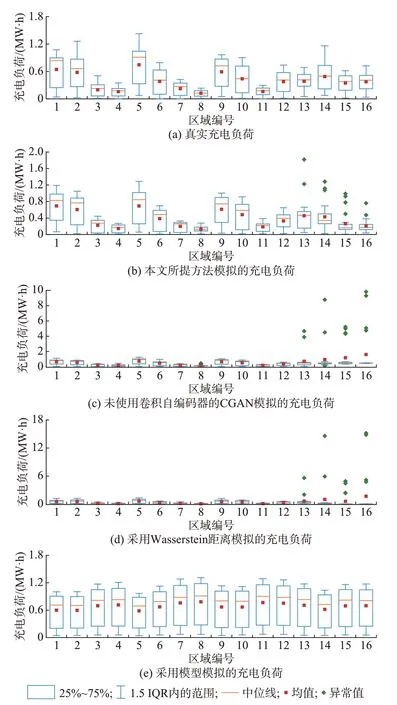
图5 不同方法生成各区域的充电负荷箱形图Fig.5 Box plots of charging load of each area generated by different methods
验证本文所提充电负荷模拟方法在不同场景下的有效性。首先,针对高比例电动汽车接入场景,采用了文献[9]基于模型的充电数据模拟方法生成数据。该模型描述了稳态下交通网车流的均衡状态。其次,针对小规模的电动汽车接入场景,根据真实的滴滴出行网约车轨迹数据,逐车逐订单地计算了每一位网约车司机的充电时间和充电地点,形成了基于轨迹的充电负荷模拟数据。在这两种场景下,本文方法都取得了良好的效果,能够较好地学习得到交通出行模式与充电负荷的对应关系。然而,模拟得到的充电负荷数据与实际数据不完全相同,存在一定局限性。在未来的研究中,随着电动汽车的大规模推广,将通过收集更高质量的电动汽车交通信息与充电负荷的对应数据,进一步验证和提高本文方法的实用性。
4 结语
针对交通网中不同电动汽车出行模式与其随机性对充电站充电负荷的影响,本文提出了一种基于数据驱动的卷积自编码器和CGAN 的充电负荷场景生成方法。首先,采用由卷积神经层和转置卷积层组成的自编码器对交通出行模式矩阵进行降维并得到特征信息,显著降低了CGAN 所需处理的条件信息的维数,降低了训练难度,并显著地提升了CGAN 的表现。其次,采用软间隔SVM 作为CGAN 的损失函数,能取得比Wasserstein 距离度量更优越的模拟效果。算例分析以西安市主干道路网络为例验证了所提方法的有效性。结果表明生成的充电负荷场景不仅能逼近充电负荷的整体分布,而且可以反映充电负荷受不同交通出行模式影响的时序特性。另外,本文通过基于车辆历史轨迹分析的实际算例进一步说明了本文方法的适用性和良好的潜力。利用本文方法可以模拟充电负荷分布,有利于配电网安全经济运行。此外,本文方法可以定位配电网薄弱环节,为下一步充电站和配电网规划提供数据支撑。
应当指出,本文方法存在一定局限性。首先,本文的训练数据通过模拟生成,缺少实际数据。其次,本文方法注重考虑“交通出行模式-充电负荷场景”的数据对应关系,并未直接对交通网建模。在未来的工作中,针对以上局限性,一方面将搜集整理实际公共充电站充电数据;另一方面将研究交通网的拓扑信息表征方法,完善随交通网拓扑变化的充电负荷场景生成方法,进一步提升本文方法的实用性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
——编码器

