基于多目标的竞争粒子群优化算法的研究

王 彬， 王丹妮， 江巧永， 杨家杰

(1.西安理工大学 计算机科学与工程学院， 陕西 西安 710048；2.滑铁卢大学 数学院， 加拿大 滑铁卢 N2L 3G1)

近年来，随着时代的发展与科技的进步，出现的许多复杂问题都已无法通过简单的模型求解，这些问题的决策变量多、问题规模大、数学性质复杂，被归类称为大规模问题[1]。因此，设计高效可靠的算法解决大规模问题是十分必要的。

针对这些优化问题，学者们提出了大量的启发式随机优化算法，进化算法就是在这种背景下提出的。受自然界生物进化的启发，如帝王蝶优化算法(MOB)[2]、大象放牧优化算法(EHO)[3]、磷虾群算法(KH)[4]等，因其操作简单、优化性能强的特点，在过去几十年中得到了快速发展，但是，进化算法在优化大规模问题时仍存在一些不足，因此，很有必要利用算法的学习能力[5]，研究出高效可靠的算法来解决大规模优化问题。

目前，针对大规模问题的进化算法主流解决策略[6]分为三类：一是静态的协同进化，即将复杂的高维问题分解成简单的低维问题进行优化求解；二是动态的协同进化，即利用分组策略将不可分的决策变量分在不同组，给予不同组一个权重向量[7]，将对问题的优化转化为对权重的优化。前两种解决策略都要在算法的前期求解决策变量之间的相关性，这样会耗费大量的时间和精力。三是整体进化，这是一种不使用分组策略的算法，主要是针对大规模问题的特点，在原有的算法中加入一些搜索策略或者是利用新的进化机制等方式来提升原有算法的寻优能力。

竞争粒子群优化算法(CSO)[8]就是整体进化的新兴代表，由于该算法结构简单、性能良好，因此在求解工程类优化问题时得到了广泛应用，且备受关注。为进一步提高算法的性能，不少科研人员都基于该算法进行了改进。2019年，Mohapatra等[9]进一步提出了ICSO，使用的是三竞争机制，它将这种遗传概念与CSO结合起来，以便更快地收敛。2020年，Zhang等[10]提出了CSO-MA，它通过变异种群中的输家来增加种群多样性，提高探索能力。同年，Xiong等[11]提出了WLCSODGM，其对优胜者领先的搜索策略和动态高斯变异算子的引入，有效地解决了传统CSO容易陷入局部最优的弊端。

然而，已有的CSO算法通常是以适应度值的大小作为参考依据来判断算子的优劣，但是，衡量粒子群算法性能的关键标准有两个：收敛速度和全局搜索能力。因此，如何平衡粒子收敛速度和全局搜索能力是有效改进算法的关键。

基于以上考虑，本文通过主动学习种群的多样性来构建多目标模型，在原有的评判基础上，将多样性也作为评估粒子优劣的条件，从而平衡种群的探索与开发能力。最后，在测试函数集CEC2008上，将本文所提算法与其他改进算法进行对比，验证本文算法的有效性。

1 相关理论

1.1 竞争粒子群优化算法

粒子群优化算法(PSO)是基于模仿群居动物的群居行为而产生的算法，其概念简单且搜索效率较高。在PSO的基础上，CSO引入了生物学中的适者生存竞争机制，不用在每一次更新时都要记住个体最优值与全局最优值。它是在一个种群内采用成对竞争机制，使用两两比较的模式更新种群。

一般情况下，考虑的都是问题最小化：

minf(X)s.t.x∈X

(1)

式中：X∈Rn是可行解解集；n表示搜索空间的维度，即决策变量的数量。

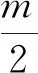
竞争后输家的更新公式为：

Vl,j(t+1)=R1(k,t)Vl,j(t)+R2(Xw,j(t)-

(2)

Xl,j(t+1)=Xl,j(t)+Vl.j(t+1)

(3)

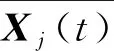
1.2 多目标优化

实际应用中，通常会遇到多个目标需要同时优化的问题，这类问题统称为多目标优化问题[12](multiobjective optimization problem, MOP)，其数学公式为：

(4)

式中：X=(x1,x2,…,xn)被称为决策变量，也是n维的决策空间；fi(x)(i=1,2,…,m)是第i个被最小化的目标；gj(x)(j=1,2,…,q)定义为第j个不等式约束；hk(x)(k=1,2,…,p)定义为第k个等式约束。此外，所有的约束决定了可行解的集合Ω，Y={F(x)|x∈Ω}被称为目标空间。

对于多目标问题而言，一个问题的优化可能会导致另一个问题的退化，因此，对于多目标问题的优化，很难找到一个同时满足各个问题最优值的解，而是找到一个平衡各个目标的Pareto最优解集。

2 研究动机

2.1 CSO在多样性方面存在的问题

收敛性分析是刻画竞争粒子群优化算法动力学行为的一个重要方面，同时也是确保竞争粒子群优化算法可靠性的基本前提。文献[8]证明发现，CSO具有良好的收敛性能，但却无法保证种群收敛到全局最优，且由于CSO的二元锦标竞争机制，每次迭代只依赖一半的粒子在搜索空间中进行开发，对种群的搜索能力有很大的限制。因此，有必要通过提高种群多样性来确保种群尽可能地收敛到全局最优。

2.2 解决思路

为了有效平衡种群的探索与勘探能力，在原有CSO以适应度值作为评价标准的基础上，加入另一个评价标准——多样性,这样不仅能兼顾个体的收敛速度，同时也能考虑到全局搜索能力。如图1所示，多样性的引入，将原本的单目标模型转化为多目标模型。

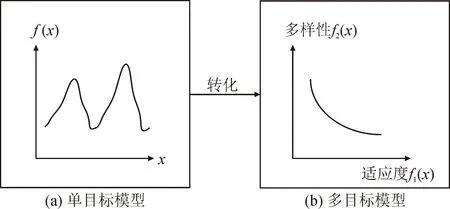
图1 单目标模型转化为多目标模型Fig.1 Single objective model transformed into a multi-objective model

3 基于多目标的竞争粒子群优化算法

基于以上考虑，本节提出了一种基于多目标的竞争粒子群优化算法(MOCSO)，不同于已有的CSO，MOCSO引入了多目标模型，将原本的单目标模型转化为多目标模型，从而在保证原有收敛性的基础上，提高了算法的开发能力，有效平衡了种群的开发与探索能力。此外，选择策略增加了随机性，在引导种群进化方向的同时，可防止种群陷入局部最优。

3.1 构建多目标模型

事实上，种群中个体的价值不仅仅取决于它的适应度值，当它与其它个体交配时，个体在解空间中产生足够分散的后代的能力也是非常重要的，因为它有助于有效且详尽地探索解空间。因此，在种群进化过程中，要尽可能使个体的探索能力和开发能力达到一个平衡，既要考虑尽快地达到全局最优解，也要考虑个体对种群多样性的影响。基于以上原因，本文采用多目标模型。模型如图2所示，将种群中的所有个体按照支配关系划分在不同的非支配层中，很明显，第一层的个体要比第二层的个体表现性能好，以此类推。

图2 多目标模型的非支配排序Fig.2 Non dominated sorting of multi-objective

以个体适应度值函数与个体多样性度量函数为横纵轴，表示要优化的两个目标函数：

适应度：ffitness(xi)=f(xi)

(5)

(6)

由于个体适应度值越小，代表其越接近种群最优解，而多样性值越大，有利于在种群更新时生成尽可能分散的解，防止算法陷入局部最优。因此，与种群中与每个个体有关的两项目标可界定为：

minffitness(xi)

(7)

min(-fdiversity(xi))

(8)

其中，多样性采用欧氏距离，因其操作简单，易于计算。

(9)

采用非支配排序，将种群中的所有个体都划分在不同的非支配层中，每一层的个体性能整体都要优于后一层的，但在同一层面的个体都相互为非支配关系。

3.2 概率随机选择策略

非支配排序已经将个体进行优劣划分，为了有效平衡种群的探索与开发能力，在CSO中引入基于排序的选择策略[13]，通过概率确定当前的输家和赢家。目的是让表现良好的个体仍能保留自己的优秀基因，从而有效地控制种群的进化方向，加快种群收敛速度。但表现较劣的个体也有可能被选为赢家，这样有利于增加种群多样性，防止陷入局部最优。详细策略步骤如下。

1) 编号分配

环境选择策略考虑了个体对种群收敛性和多样性贡献的大小，并按照其在Pareto前沿上的顺序进行全排序。其中，性能表现良好的个体排在首位，性能较差的个体排在末位，即越优质的个体，指标就越小。为了以较大的概率选择性能较好的个体作为赢家，需要重新定义种群编号。可表示为：

Ri=NP+1-i,i=1,2,…,NP

(10)

式中：NP是种群规模；i是当前种群中第i个个体的指标。

2) 选择概率

根据式(10)中对个体编号的计算，第i个个体被选择为赢家的选择概率为：

(11)

因此，适应度值较低和多样性较好的个体将有很大的概率在排序种群中被选择作为赢家。

3.3 算法描述

基于以上对MOCSO的描述，多目标的竞争粒子群优化算法(MOCSO)的算法流程如表1所示。与经典CSO相比，MOCSO主要增加了一个双目标模型(step2.1和step2.2)和选择策略(step2.4)。

4 实验及分析

4.1 对比算法

为验证所提算法的有效性，本节引入6种对比算法，分别是：竞争粒子群优化算法(CSO)[8]、继承的竞争粒子群优化算法(ICSO)[14]、改良的竞争粒子群优化算法(MCSO)[15]、动态分组的竞争粒子群优化算法(CSO-DG)[16]、反向学习的竞争粒子群优化算法(OBLCPSO)[17]、排序学习的竞争离子群优化算法(RBLSO)[18]。

4.2 测试函数

在CEC2008上对MOCSO进行数值实验，为了确保运算的准确性，每个算法在每个测试函数上独立运行51次。CEC2008的测试函数主要分为两类：单模测试函数(F1～F2)、多模测试函数(F3～F7)。

表1 MOCSO的算法流程Tab.1 Flow chart of MOCSO

4.3 参数设置

所有仿真实验的测试平台都是相同的，均为2.60 GHz CPU和4 GB RAM，Microsoft Windows 10操作系统，Intel(R) CoreTMi5-3230M；测试软件是Microsoft Windows 10操作系统下的MATLAB 2016a。

为评估MOCSO的有效性，将MOCSO与现有CSO的不同改进算法进行比较，其公共参数设置如表2所示。

表2 对比算法中的公共参数设置Tab.2 Public parameter setting in comparative algorithm

此外，本文采用两个标准来评估算法的性能：

1) 收敛速度：绘制了不同类型测试函数的收敛曲线，直观地显示出算法的收敛情况，并反映出最优解在各个算法之间的误差值；

2) 统计分析：为了更客观地比较两种算法的性能，本文采用0.05显著性水平的Wilcoxon秩和检验对实验结果进行统计和分析， 如果得到的概率值小于0.05，则认为两种算法的性能有显著差异，用1表示，否则为无显著差异，用0表示。

4.4 实验结果及分析

表3、表4和表5分别记录了MOCSO与6组对比算法在CEC2008测试函数集上的相关实验结果，并给出了统计分析性能比较。从最后一行的“w/s/l”值可以看出，MOCSO与其他算法存在显著差异，其在大多数基准测试函数上的整体效果明显优于其他算法。

进一步分析可知，MOCSO在每个测试函数中的排名一般位于前两名，整体收敛效果良好，这是因为在评判标准中加入了多样性，又保留了原始算法中粒子优秀的探索能力，同时考虑到粒子的勘探能力，使得种群在更新过程中能有效平衡粒子收敛速度和全局搜索能力。

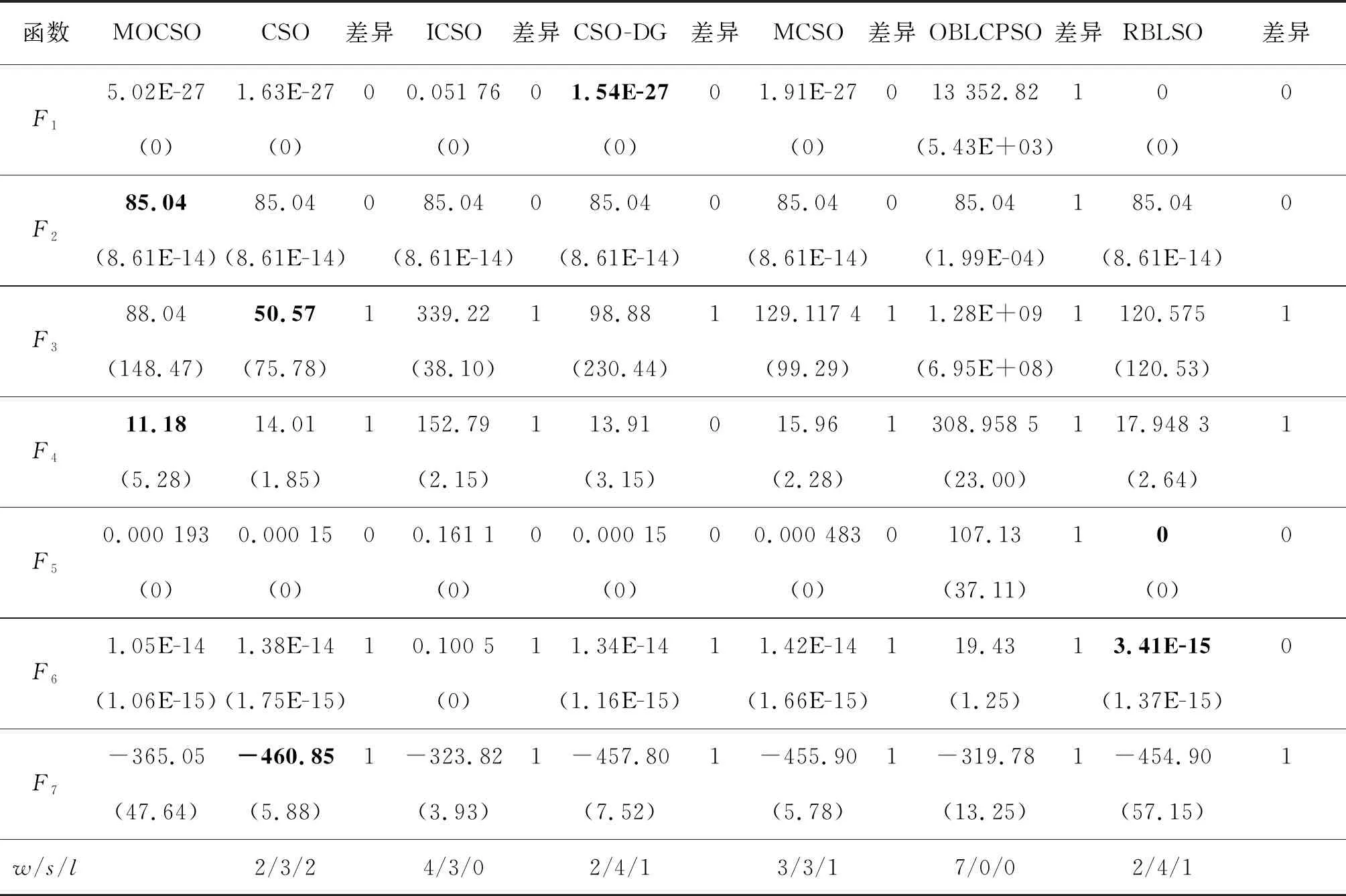
表3 MOCSO与6组对比算法在30维的CEC2008上独立运行51次的统计结果Tab.3 Statistical results of MOCSO and 6 groups of compared algorithms running 51 times independently on 30 dimensional CEC2008

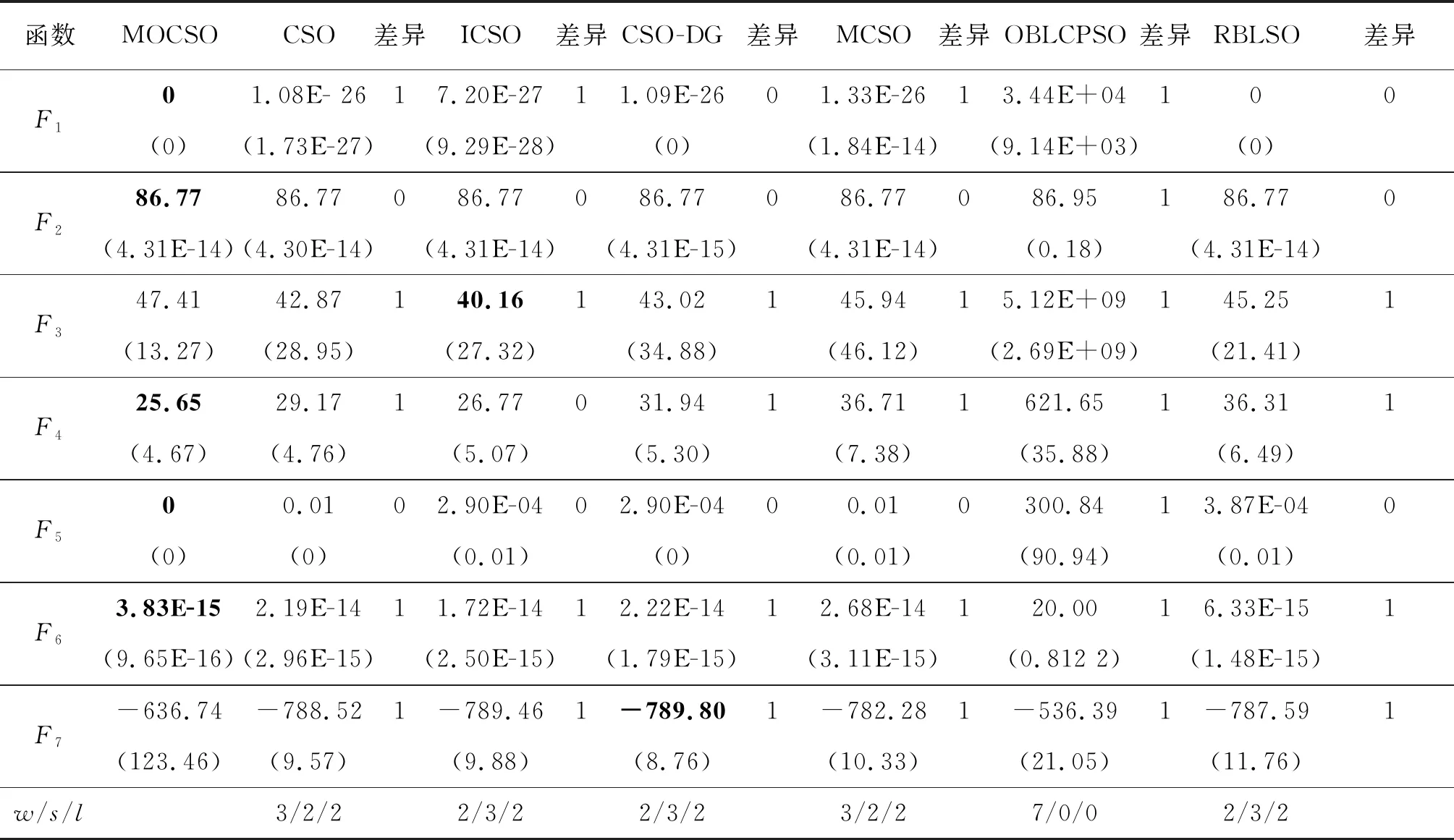
表4 MOCSO与6组对比算法在50维的CEC2008上独立运行51次的统计结果Tab.4 Statistical results of MOCSO and 6 groups of compared algorithms running 51 times independently on 50 dimensional CEC2008

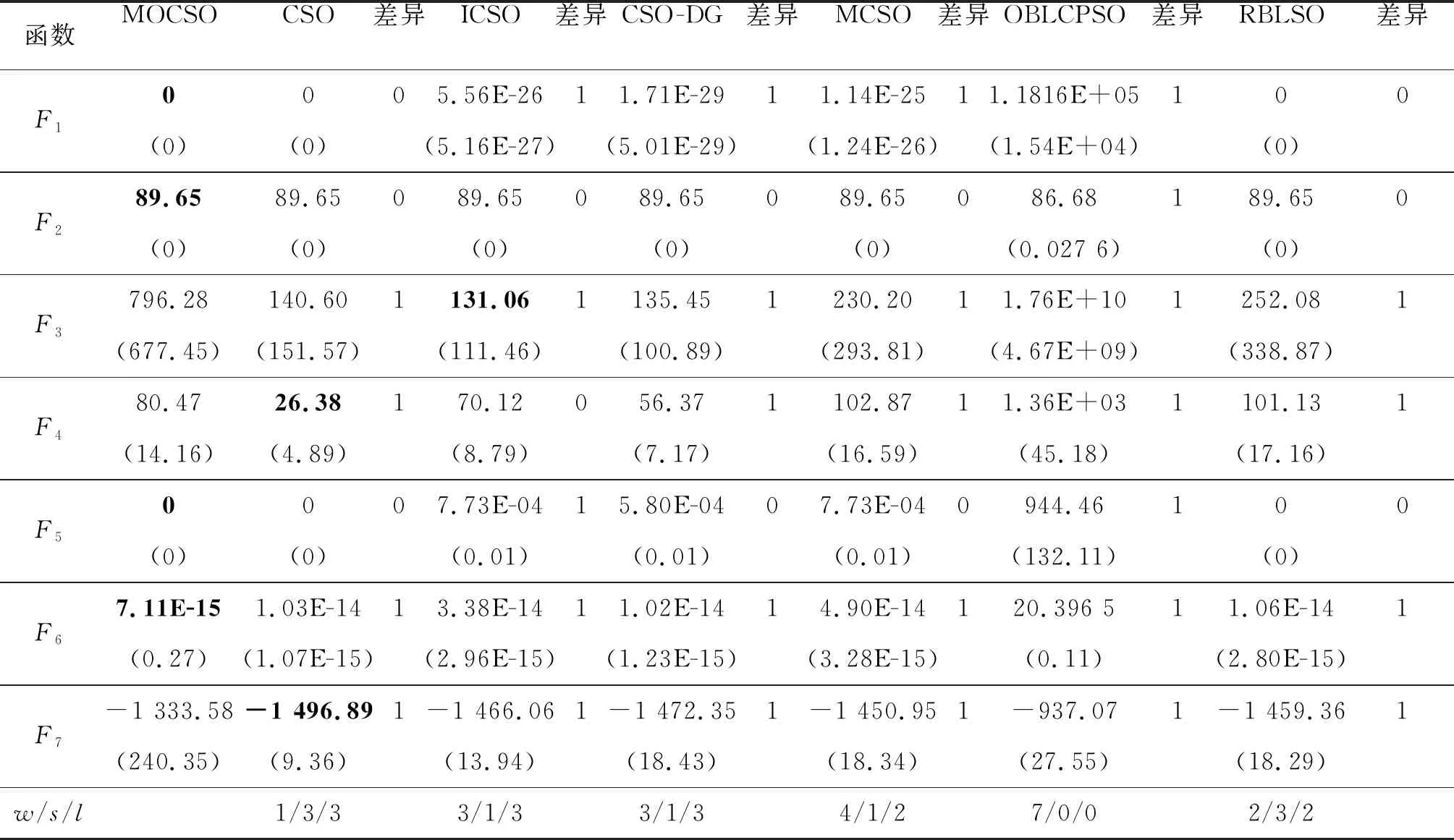
表5 MOCSO与6组对比算法在100维的CEC2008上独立运行51次的统计结果Tab.5 Statistical results of MOCSO and 6 groups of compared algorithms running 51 times independently on 100 dimensional CEC2008

从秩和检验的结果来看，MOCSO在30维、50维和100维上，有超过一半的基准函数其性能明显优于其他对比算法，为了更直观地比较MOCSO与6组对比算法的收敛效果，图3给出了MOCSO在测试函数集CEC2008上与其他算法的收敛速度的对比图，从图3中也可以看出，MOCSO的整体收敛效果还是具有一定优势的。

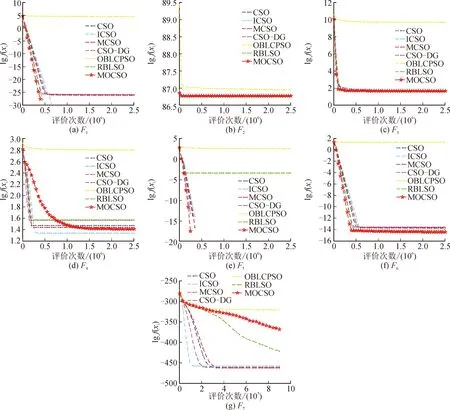
图3 MOCSO与6组对比算法在50维的7个测试函数上的收敛曲线Fig.3 Convergence curves of MOCSO and 6 groups of compared algorithms for 7 test functions of 50 dimensions

4.5 计算效率分析

通过比较MOCSO与其他6组算法的复杂度来分析MOCSO的计算效率，结果如表6所示。

表6 7组算法的复杂度对比Tab.6 Complexity comparison of seven groups of algorithms

由表6可知，MOCSO的计算成本要高于其他改进算法，因为MOCSO设置了多目标，因此每次迭代需要消耗大量额外的计算资源，为降低成本，该算法还有待进一步改进。

5 结 论

为了提高竞争粒子群优化算法(CSO)的性能，进一步平衡种群中粒子的探索能力与开发能力，本文提出了一种基于多目标的竞争粒子群优化算法，它在原有CSO的基础上提出了以下改进：

1) 设计多目标演化机制，在演化过程中考虑了适应度值和拥挤距离，即在兼顾原有算法收敛速度的同时，又保留了种群的全局搜索能力；

2) 引入随机选择策略，在每一次迭代中选择输赢家，这种策略在很大程度上保存了种群中的优秀基因。

在CEC2008测试函数集上对MOCSO算法进行数值实验，并与CSO、ICSO、CSO-DG、MCSO、OBLCPSO、RBLSO进行性能对比。实验结果表明，与现有CSO及其改进方法相比，MOCSO在测试函数集上的整体效果明显占优。

通过仿真实验，虽然验证了MOCSO具有一定的有效性，但由于该算法设置了双目标，使得计算效率下降，其后续还有待进一步改进。