基于小波变换的VFFRLS锂电池参数辨识

任碧莹， 徐玮浓， 孙 佳， 孙向东

(西安理工大学 电气工程学院， 陕西 西安 710054)

电动汽车锂离子电池因其能量密度高、自放电率低、安全可靠等优点被广泛应用[1]。其应用时需要安全稳定的工作环境，而对荷电状态(state of charge，SOC)的准确估计是保证其性能充分发挥，避免过充、过放并延长使用寿命的重要基础[2]。高精度的SOC估计依赖于电池模型参数的准确度，因此，提高电池模型参数辨识的精度十分重要。

基于等效电路模型的参数辨识方法中，以递推最小二乘法(recursive least square，RLS)的应用最为广泛。RLS计算量小，简单易实现，但随着系统获取的数据量的增大，新数据提供的信息逐渐被旧数据淹没，使算法失去校正能力，即出现“数据饱和”现象[3,4]。为了避免该现象的发生，要求加大新数据在计算中所占的权重，因此，文献[5,6]研究了含遗忘因子的递推最小二乘法(forgetting factor recursive least square，FFRLS)，通过引入遗忘因子，使系统能够更加充分地利用新数据中的信息，降低旧数据对系统的影响，从而使系统参数得到更准确的估计，提高时变系统的辨识精度。为了更进一步提高时变系统的辨识精度，许多学者以FFRLS为基础，从算法本身出发，根据其性能对算法进行改进。文献[7]研究了一种VFFRLS算法，它是根据预测误差确定遗忘因子，并随算法的进程而自适应地改变。当信号存在剧烈波动的情况或存在数据错误或丢失的情况时，该方法可以有效提高参数识别的收敛速度并减少辨识错误，但该方法高效的收敛能力可能会受到预测误差的影响。文献[8]提出了一种根据模型中各参数自身的物理特性来独立调整遗忘因子的方法，以适应深度放电范围和高动态工作条件下参数的极大变化，然而该方法主要是为了保证锂电池在深度放电情况下对参数的动态跟踪精度。文献[9]指出，模型中各单个参数的变化速率可能存在偏差，单一的遗忘因子难以衡量参数辨识能力与收敛性和稳定性之间的关系，因此在进行参数辨识时，需要对不同参数进行不同速率的校正，故该文献提出了一种基于解耦多遗忘因子的递推最小二乘法，对具有不同变化率的各个参数进行独立跟踪，但该算法的应用需要以简单模型为前提，在更精确更高阶的模型中难以应用。

此外，还有许多学者就外部参数对辨识效果的影响问题对算法展开研究，由于实际应用中存在电磁干扰或传感器分辨率低的情况，电池系统容易受到噪声的意外感应，出现变量误差问题[10-12]。文献[10]提出了一种偏置补偿递归最小二乘法以克服辨识固有误差，但该方法需要噪声统计信息，而统计信息较难获得。文献[13]提出了一种自适应遗忘递归总最小二乘法，并结合带有增益调度的Luenberger观测器来补偿噪声影响，但计算量大。

通过对各文献的分析可知，遗忘因子会影响算法对噪声的敏感度以及收敛性的优劣程度，在进行大量数据分析时，可能存在不易平衡分离噪声与收敛性的问题。因此，本文提出基于小波变换的可变遗忘因子递推最小二乘法(WVFFRLS)来进行电池参数的动态辨识。该算法具有准确性高、收敛性快的辨识效果，通过与VFFRLS的实验对比，验证了本文所提出的参数辨识方法的可行性。

1 VFFRLS参数辨识存在的问题

1.1 锂电池模型

目前，锂电池等效模型主要有内阻模型、阻容模型、PNGV模型、GNL模型以及戴维南模型。其中，戴维南模型又称n阶RC模型，因其能够反映出电池内部参数与外部参数如温度与电流之间的关系，并且能够良好地表征电池的动态特性，故应用更为普遍[3]。而该模型的精度、计算复杂度与应用难度皆随RC阶数的增大而增大。因此，综合考虑计算复杂度及精度，锂电池等效模型通常选取二阶RC等效电路模型。锂电池二阶RC等效电路模型如图 1所示，模型中的参数包括电池内阻R0，极化电阻R1、R2，极化电容C1、C2，两个并联RC分别表示了电池的电化学极化过程与浓差极化过程。UOC表示开路电压，UL表示端电压。

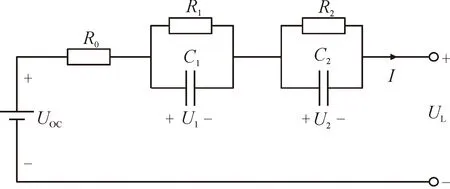
图1 锂离子电池二阶RC等效电路模型Fig.1 Second-order RC equivalent circuit model of a lithium-ion battery

对二阶RC等效电路模型的时域关系进行拉普拉斯变换，得到参数与观测值的关系表达式：

UL(s)=

(1)

令U(s)=UOC(s)-UL(s)，τ1=R1C1，τ2=R2C2，a=τ1τ2，b=τ1+τ2，c=R0+R1+R2，d=R0(τ1+τ2)+R1τ2+R2τ1，对式(1)进行离散化处理并整理，得到可用于最小二乘法参数辨识的差分方程：

(2)

其中，k0=a+bT+T2，k1=(2a+bT)/k0，k2=-a/k0，k3=(aR0+dT+cT2)/k0，k4=-(2aR0+dT)/k0，k5=aR0/k0。

式(2)可写为如下形式：

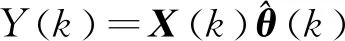
(3)

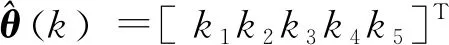
通过辨识算法得到待估参数k1、k2、k3、k4、k5的估计值，进一步反推可得出对应的电池参数R0、R1、R2、C1、C2的值。

1.2 VFFRLS中遗忘因子对辨识算法的影响

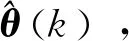
(4)

(5)

(6)

(7)

式(7)中的各变量表达如式(8)～(12)，其中e(k)为先验误差，q(k)为后验误差，公式中的α和β均为加权因子。

(8)

(9)

(10)

(11)

(12)

根据式(7)可看出，遗忘因子与噪声功率存在一定关系，噪声会通过影响遗忘因子进而对整个算法辨识情况产生影响。

实际系统中通常存在噪声，含噪声的系统模型可表示为：

d(k)=y(k)+v(k)=x(k)θ+v(k)

(13)

式中：d(k)为系统中含有噪声的输出；y(k)=x(k)θ为系统真实值；v(k)为系统噪声。

要使该模型实现参数的最小二乘法估计，须要求所估值的误差平方和最小，即辨识算法依靠估计误差来驱动，其误差驱动信号为：

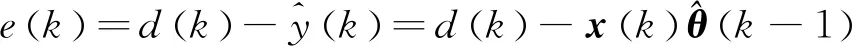
(14)

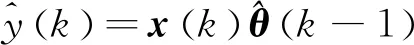
(15)

再将Y(k)结合式(13)可得：

(16)

根据式(15)和式(16)可知：

(17)

当λ非常接近1且k足够大时，可以认为公式(17)中噪声信息的数学期望为0，如式(18)：

(18)

因此，式(17)可写作：

(19)

此时，系统参数估计值即为参数实际值。又根据式(14)可知，误差信号即为系统噪声：

e(k)≅v(k)

(20)

当λ较小时，λn≪1，则有：

(21)

此时，结合式(14)和式(17)可得：

e(k)=0

(22)

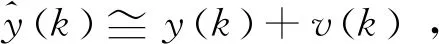
2 基于小波变换的VFFRLS算法

2.1 小波变换

小波是一种具有能量的微小波动，其能量集中于某一时间及频率上，它是对瞬时、不平稳或时变信号进行分析的有效工具。将任意信号或函数f(t)的二进制离散小波变换定义为：

(23)

其逆变换为：

(24)

式中：Ψ(t)为母小波；2m表示伸缩尺度参数；n表示平移时间参数。

以m、n为基础对信号进行多分辨分析。利用低通滤波器和高通滤波器分别对所给信号进行滤波，将该信号分解为低频信号和高频信号两个部分。不同分解层上的信号f(t)的缩放尺度和小波系数为[15]：

(25)

式中：cj,k为低通滤波器输出后所重构原始信号的近似信号；h为低通滤波器的系数；dj,k为高通滤波器输出后所重构原始信号的细节信号；g为高通滤波器的系数。可由各级信号重构出上级小波公式：

(26)

2.2 基于小波变换的VFFRLS算法

该方法首先对观测向量进行小波分解重构，将所得的低频近似信号作为VFFRLS算法中的估计参考值，以所得的高频细节信号作为系统噪声功率，再以该噪声功率为准去更新λ。此时，对于作为估计参考值的低频信号，稳态时的信息向量已经更为精确，λ的作用可近似认为仅提高系统跟踪能力；而对于用以更新λ的高频信号，小波变换所得的噪声信息更为精确，在系统存在波动时，能够更好地提高算法的收敛性。

不同的小波基在处理不同信号时各有特点，一般来讲，Daubechies(Db)小波族因其良好的正交性和紧支撑性，经常被应用于信号处理。对测得的电压信号进行j层小波分解重构，分别得到作为估计参考值的低频近似信号Aj和作为系统噪声功率的高频细节信号Dj(j为层数)，其j级重构原理如图 2所示，其中C0为分解重构后的电压信号。本文选取Db4小波基进行分解和重构。

图2 重构过程示意图Fig.2 Reconfiguration diagram

根据上述思想，基于小波变换的VFFRLS算法应用于锂电池参数辨识时，其具体步骤为：

步骤1：对观测向量电压电流进行小波分频，并重构观测向量的低频信号和高频信号；

步骤2：因初始化参数选取不当会使系统参数辨识收敛性不佳，甚至不收敛，所以本文通过采用最小二乘法，对大于辨识参数个数的多组参数进行成批处理来优化初始化参数，得到初始化的待估参数θ(0)、协方差矩阵P(0)及遗忘因子λ(0)；

步骤3：将所得观测向量的低频信号作为VFFRLS算法中的信息向量X(k)。

步骤6：根据式(6)更新协方差矩阵P(k)。

教师在实施激励性课堂教学时，要时刻谨记师生平等的原则，遵循以学生为教学主体的教学理念，构建和谐友善的师生关系，进而大大提高物理课堂教学效果。

步骤7：由式(8)～(12)计算噪声功率σe(k)和σq(k)。

步骤8：将步骤1所得的高频信号作为系统噪声功率σv(k)代入式(7)，用以更新遗忘因子λ(k)。

步骤9：循环至数据处理完毕。

算法的具体流程如图3所示。

图3 基于小波变换的VFFRLS算法流程图Fig.3 Flow chart of VFFRLS algorithm based on wavelet transform

3 实验验证

在参数辨识前，首先进行UOC与SOC之间的曲线拟合以及递推初始值的优化，在此基础上，再进行参数辨识算法的验证、比较和分析。本文采用山东威能公司生产的磷酸铁锂电池对算法进行验证，该电池参数如表1所示。测试平台如图4所示，由被测锂离子电池、专用电池测量设备、数据线和带有专用测试软件的计算机组成。

表1 锂电池参数Tab.1 Lithium-ion battery parameters

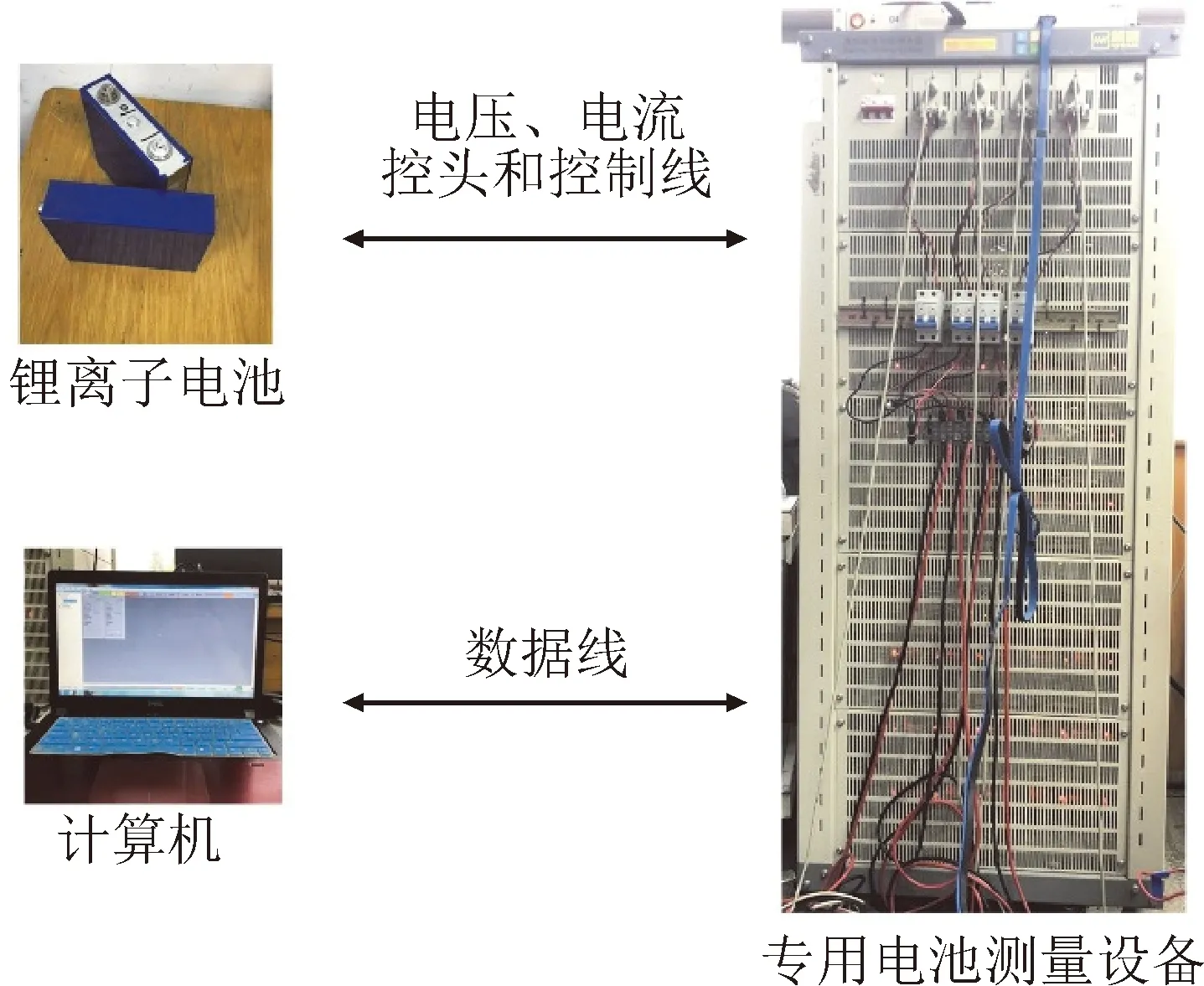
图4 电池测试平台Fig.4 Battery testing platform

采用0.33C标准速率电流对锂电池进行间歇恒流充放电实验，对实验数据进行拟合，分别得到充放电时的拟合曲线，如图5所示。

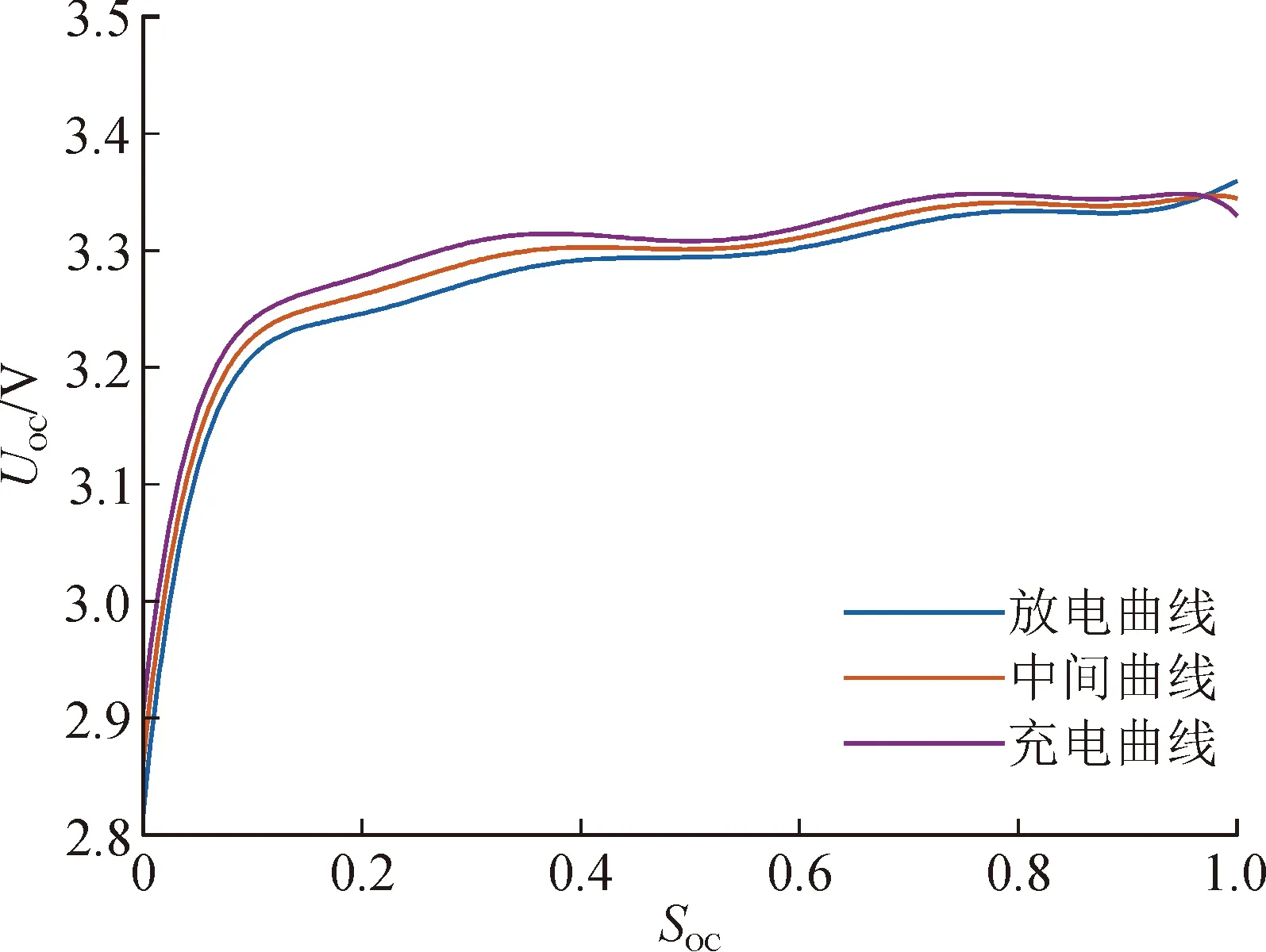
图5 UOC-SOC关系曲线Fig.5 Relationship curves of UOC and SOC

由图5可看出，整个充放电过程存在“迟滞现象”[16]，故取充放电曲线的中间曲线作为开路电压UOC与SOC(以参数SOC表示)的关系曲线：

UOC=-302.7SOC8+1333SOC7-2432SOC6+

2377SOC5-1348SOC4+499.3SOC3-

(27)

85.82SOC2+8.878SOC+2.86

3.1 递推初始值的对比和选取

利用成批型的最小二乘法，对大于所需辨识参数个数的N组数据，求取参数估计值θ(0)和协方差阵P(0)，并将所得结果作为递推算法的初始值。

以恒流放电工况下应用VFFRLS算法的参数辨识结果为基础，分析递推初始值对辨识结果的影响，如图6所示。根据仿真结果可看出，随着N的增大，收敛性增强，但同时会引起计算量加大及耗时增长，因此，综合考虑后，最终选取N=20时的参数估计值和协方差阵作为辨识算法的递推初始值。

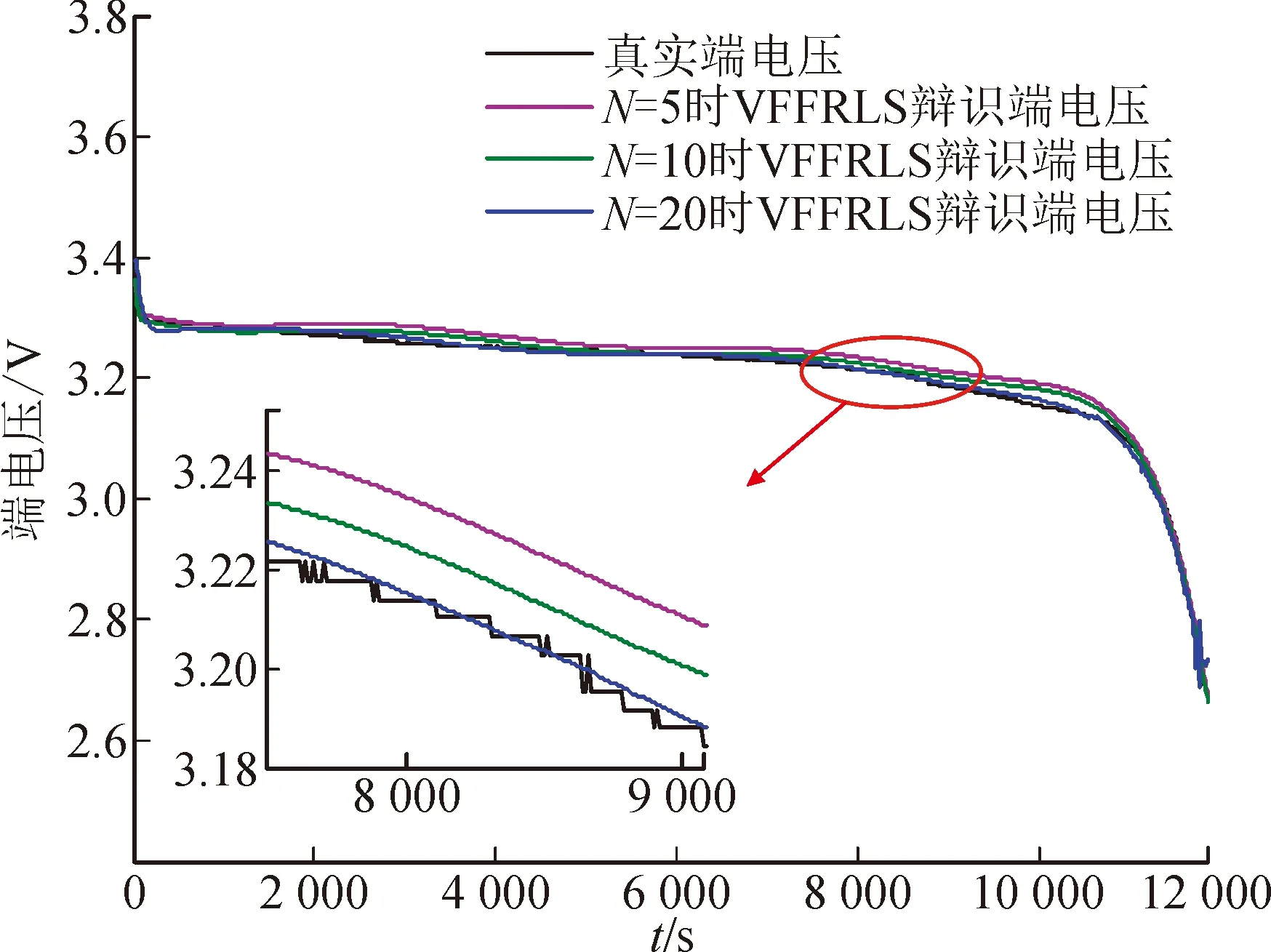
图6 不同初始值对辨识结果的影响Fig.6 Influence of different initial values on identification results

3.2 锂电池模型参数辨识

将WVFFRLS算法置于动态应力测试(dynamic stress test，DST)和间歇恒流放电工况下进行验证，并与VFFRLS算法进行对比分析，其电压电流波形如图7所示。图8为经小波变换分离出的观测量高频噪声信号。图9和图10分别显示了两种算法在DST工况和间歇恒流放电工况时锂电池参数辨识的结果。图11显示了两种工况下遗忘因子λ的变化曲线。

通过对比可看出，相较于VFFRLS算法， WVFFRLS算法具有更好的收敛性与鲁棒性，并且能够同时反映出各参数随充放电电流变化的动态特性，对电流状态具有良好的识别能力。此外， VFFRLS算法中，遗忘因子需要不断平衡算法跟踪能力与噪声敏感度，因此存在较多尖峰，而在WVFFRLS算法中，有小波辅助遗忘因子分离噪声，消除了噪声对遗忘因子的干扰，因此遗忘因子尖峰较少。

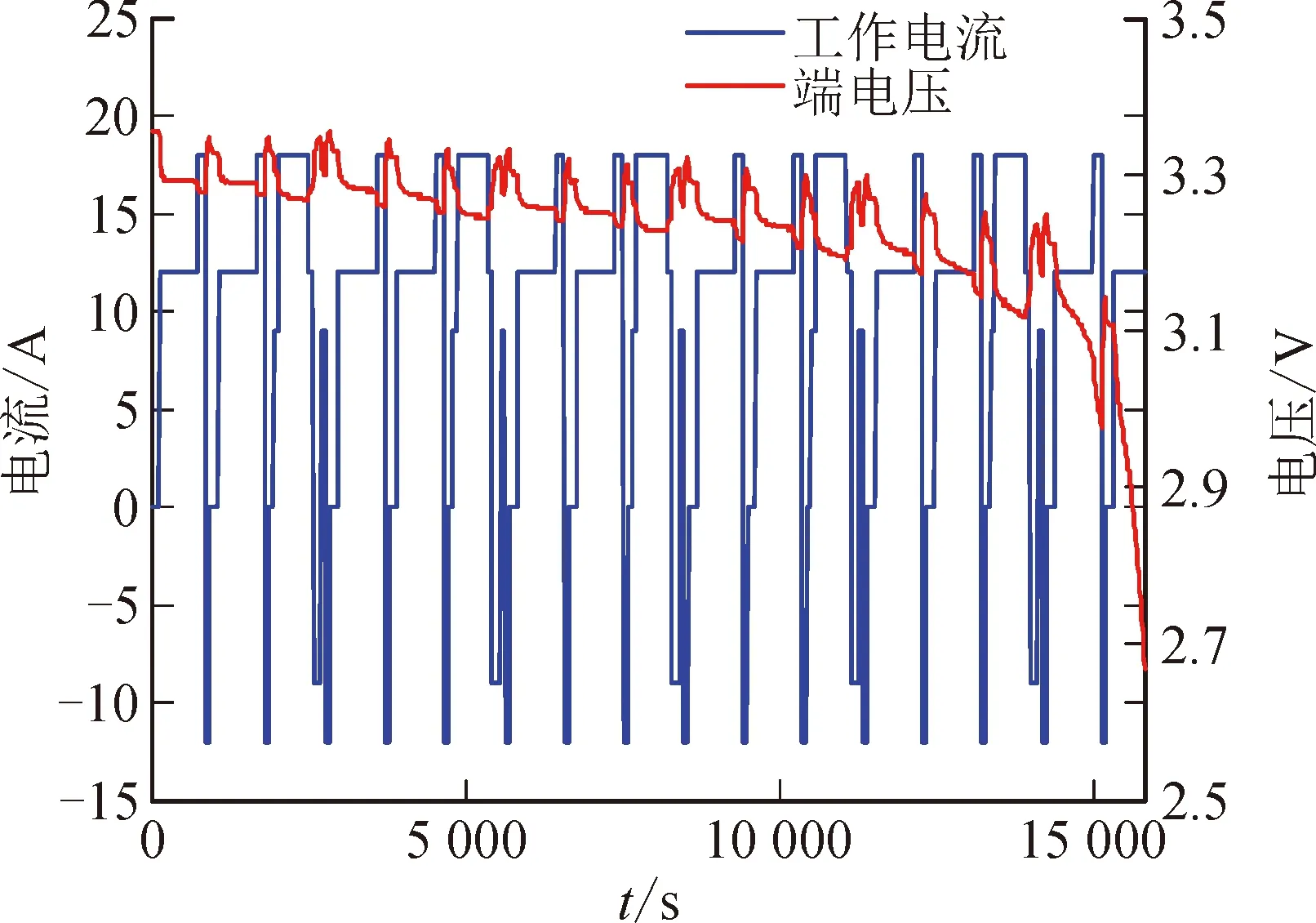
图7 DST工况的电压电流曲线Fig.7 Voltage and current curves under the condition of DST

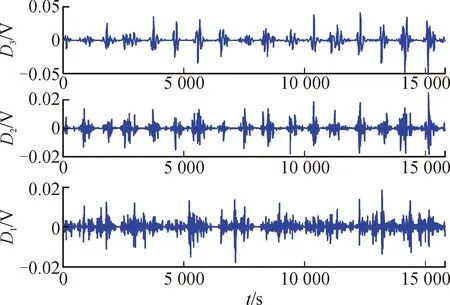
图8 小波变换所得的各层高频信号Fig.8 High frequency signals of each layer obtained by wavelet transform

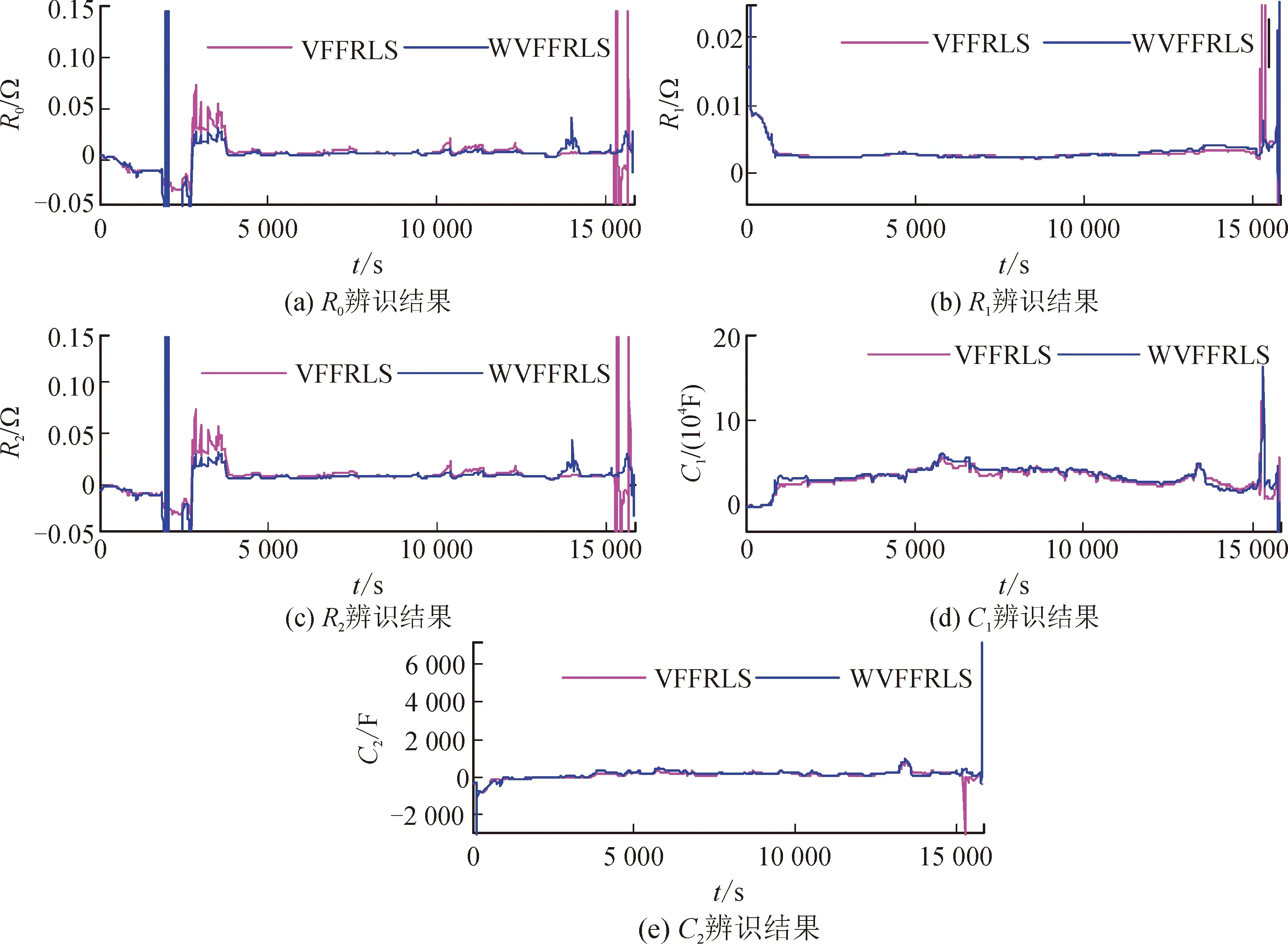
图9 DST工况下参数辨识结果Fig.9 Parameter identification results under DST condition

3.3 辨识结果分析

图12和图13分别给出了DST和间歇恒流放电工况下，以两种算法辨识结果为依据得到的锂电池模型端电压与真实端电压的对比结果。

由图12和图13可以看出，两种算法的辨识误差大多都在±2%以内，但WVFFRLS算法辨识结果的系统跟踪能力更好。

为了对VFFRLS与WVFFRLS算法进行综合评价，对两种算法下的参数辨识结果进行误差分析。误差分析主要通过比较端电压估计值与实际值之间的平均相对误差(mean square error，MRE)和均方根误差(root mean square error，RMSE)来实现[16]。根据式(28)可以得到两种算法下的辨识误差情况。

(28)

式中：UL.a为实际值；UL.e为估计值。

将本文结果与各文献所述的其他算法的辨识结果进行对比，对比情况如表2所示。

图10 间歇恒流放电工况下参数辨识结果Fig.10 Parameter identification results under intermittent constant current discharge

图11 λ的变化曲线Fig.11 Change curve of λ

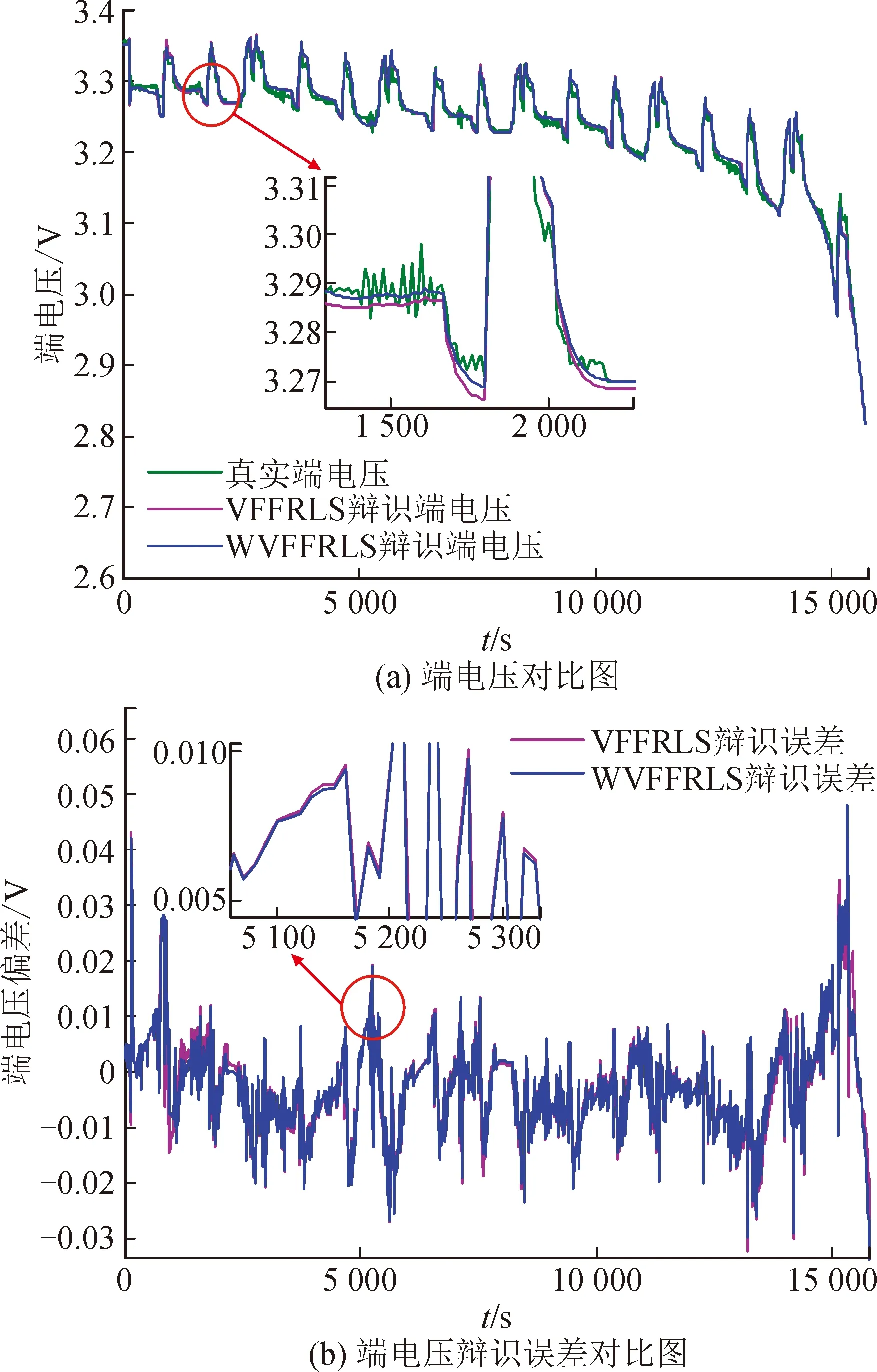
图12 DST工况下参数辨识结果对比Fig.12 Comparison of parameter identification results under DST condition

图13 间歇恒流放电工况下参数辨识结果对比Fig.13 Comparison of parameter identification results under intermittent constant current discharge

表2 不同算法误差情况对比

从表2可以看出，相较于VFFRLS算法，WVFFRLS算法的辨识结果精度更高。与文献[7]和文献[17]的算法相比，本文所提算法均体现了更好的辨识效果。与文献[13]的算法相比，WVFFRLS算法的RMRE有所下降，RRMSE相差不大，整体来讲性能更好。再结合图12和图13可以看出，不管系统处于剧烈波动状态还是相对平稳状态，WVFFRLS算法的辨识结果都更接近于真实值，算法整体表现出更好的收敛性与系统跟踪能力。

4 结 语

本文以二阶RC电路模型作为锂电池的等效模型，分析了遗忘因子在算法中的作用以及对辨识结果的影响，并针对其平衡噪声分离能力与收敛程度的问题提出了基于小波变换的可变遗忘因子递推最小二乘法。在DST工况和间歇恒流放电工况下对该算法进行验证，并与VFFRLS算法辨识结果进行对比分析。实验结果表明，相较于VFFRLS算法，WVFFRLS算法的辨识结果精度更高，能够实现更好的收敛性以及跟踪性。