旋转运动SMA层合梁动力学建模与非线性自由振动分析
王 航, 穆安乐, 黄泽波
(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048;2.西安铁路职业技术学院 机电工程学院, 陕西 西安 710026)
复合材料有着广阔的应用前景。复合材料质量轻,有很大的刚度和阻尼,其优异的力学特性使得复合材料尤其是层合材料有着非常广泛的应用前景。复合材料制成的旋转结构在很多场合下均有使用,例如汽轮机叶片、压缩机、风机叶片等。形状记忆合金(SMA)是一种非常有应用前景的智能材料。SMA在受热的情况下会表现出很大的恢复力,可以作为一种驱动器使用。这种驱动器可以制作成很小的体积,不但能省去电机驱动过程中的一些复杂的传动机构,而且有研究表明,内嵌SMA丝的层合材料制成的机械臂可以很好地抑制振动。
SMA的理论研究难点是如何建立精确的一维SMA本构关系。SMA的应变可以归结为热变形和马氏体相变两部分[1-2]。在此基础之上,有不少文献对内嵌SMA丝的复合结构进行了分析。研究的对象主要是梁、板和壳。研究显示,温度变化时内嵌SMA丝的复合梁,其自由振动的基频是不同的,SMA的体积分数对后屈曲特性的影响也是显著的,主要表现为降低热屈曲响应。当SMA的体积分数、初始应变增大时,基频的变化趋势是上升的,基频曲线同横轴的交点后移[3-4]。内力的变化趋势同基频曲线的变化趋势是相同的,屈曲变形也随着SMA体积分数的增大而减小,屈曲温度低于奥氏体开始温度时,SMA的存在可以使失稳的梁结构处于稳定状态[5]。SMA的存在减小了层合板的变形挠度[6]。SMA层合板处于复杂的物理场中时,比如在热场中受一阶气动活塞力作用时,系统的非线性颤振特性是不同的,主要表现为随着SMA体积分数的增加,稳定区域逐渐扩大,由此可得,SMA可以提高结构的稳定性[7]。Dehkordi[8]用非线性有限元与增量迭代算法进行仿真计算,发现SMA的存在降低了板的振幅。Kumar等[9]用分层理论重新描述了位移场,得到SMA丝的铺设角度越大,屈曲温度越高。Karimi等[10]在分析SMA层合板时,没有考虑系统的非线性特性,并发现板的长宽比增大时,基频整体上是上升的。相应的,在大的长宽比时,记忆合金的恢复应力对基频的影响作用下降了。文献[11]使用遗传算法获得了最佳的SMA丝铺设次序和敷设角度,获得了不同边界条件下SMA层合板的最优固有频率。可以使用广义微分求积法分析内嵌SMA丝的圆柱壳的固有振动特性。SMA层越靠近圆柱壳的内壁,系统的基频越大[12]。对于圆锥壳而言,增大半顶角能有效地增加基频;沿中性面对称布置SMA层时,可以增加基频,而单层布置时基频变小了[13]。任勇生等[14]发现,SMA层合梁非线性固有频率增大时,其振幅也是增大的,而对应线性系统没有该特性。事实上,就目前的研究成果而言,记忆合金一维本构模型是所有内嵌SMA丝层合结构的研究基础,并且,研究对象的边界条件也仅限于简支和固支的情况。而关于大范围旋转运动梁的自由振动,也有着丰富的研究成果。黄意新等[15]通过与有限元结果对比,认为Chebyshev谱方法计算的旋转梁固有频率是正确的。此外,旋转Rayleigh梁的长细比等相关参数会对临界转速产生影响,且临界转速随着长细比的增大而减小[16]。范纪华等[17]使用Bezier曲线离散动力学方程,得到不同角速度下,旋转梁厚度变化对固有频率的影响将大于宽度的影响。旋转Timoshenko梁的频率会随着转速的增加而增大,并随着长厚比的增加而减小[18]。而且在分析旋转结构的固有频率时,总是认为系统的旋转角速度是定值[19-21]。Aksencer等[22]研究了旋转层合梁的固有频率,轮毂比小于0.5时,转速增加则固有频率增加;轮毂比大于1时,会产生频率为零的情况。
通过对现有文献的总结可知,关于SMA层合结构的振动研究主要集中在基频以及热屈曲方面,而对于旋转运动SMA层合梁的非线性自由振动,尚未被涉及。本文使用Von Karman大变形理论来描述梁位移与应变的关系,建立了层合梁任意质点在惯性坐标系下的位移表达式,用Brinson模型描述了不同温度下SMA的恢复应力和马氏体体积分数。使用Hamilton原理建立了SMA层合梁大范围旋转运动的动力学方程。研究了系统参数变化时,SMA层合梁的动力学响应。基于内力恒定的假设,得到了恒定转速下,旋转SMA层合梁横向振动的动力学方程。研究了SMA在不同初始应变、体积分数、石墨纤维铺设角度以及SMA所处铺层不同时,固有频率的变化。
1 系统建模
1.1 SMA本构方程
尽管有多种描述SMA本构关系的模型,但是Brinson模型是目前主流的分析方法,大部分研究SMA热屈曲与自由振动的文献都采用了该模型[3-7]。文献[1]将SMA的变形视为由热应力引起的变形和由马氏体相变引起的形变两部分组成。依据Brinson模型,SMA中马氏体的体积分数为:
ξ=ξS+ξT
(1)
式中:ξS为应力诱发的马氏体相变体积分数;ξT为温度诱发的马氏体相变体积分数。
相变转变为奥氏体时,马氏体的体积分数为:
(2)
(3)
(4)
式中,ξ0为初始状态时的马氏体体积分数;σr是SMA恢复应力;T为温度;ξS0为初始应力诱发的马氏体体积分数;ξT0为初始温度诱发的马氏体体积分数;CA是应力影响系数。有关SMA的其他参量参考文献[5]。
又可知,SMA杨氏模量为:
(5)
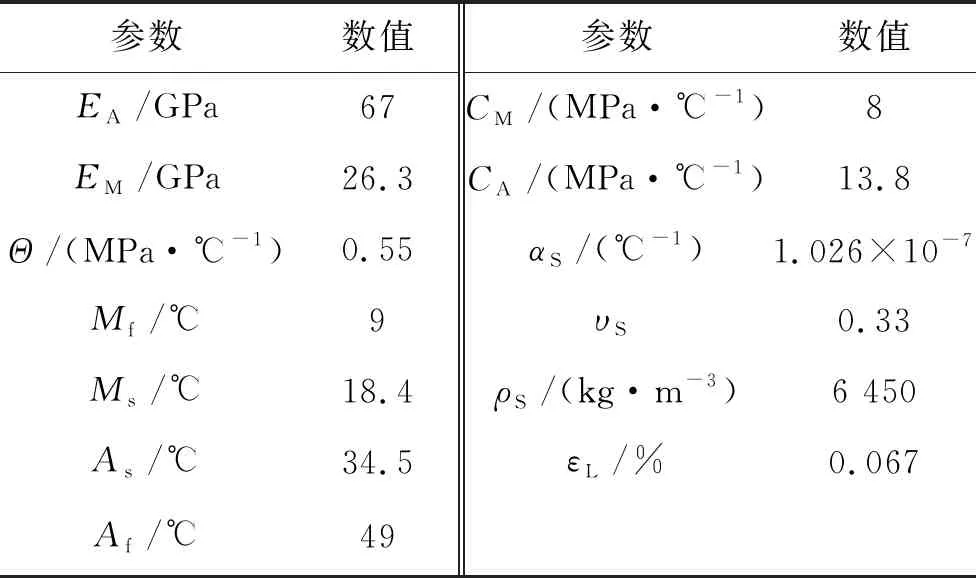
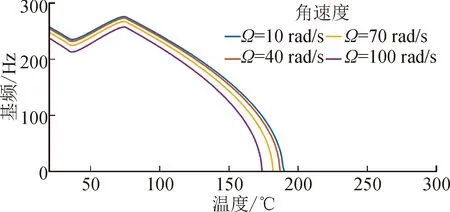
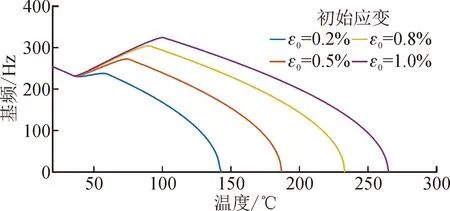
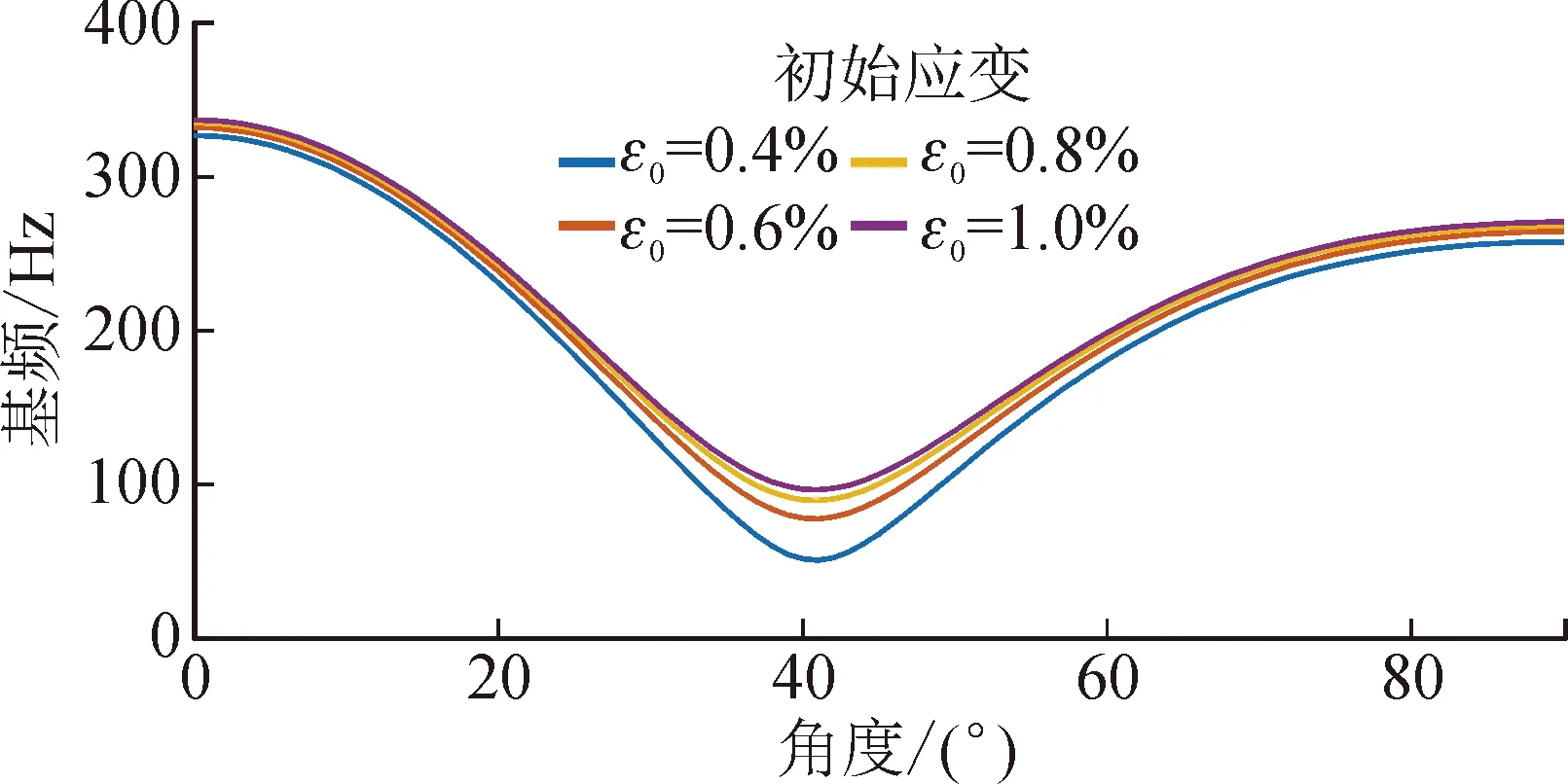
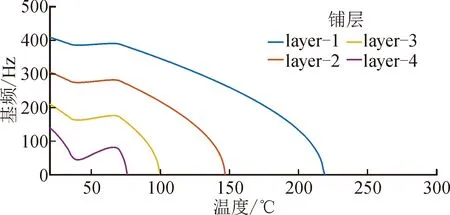
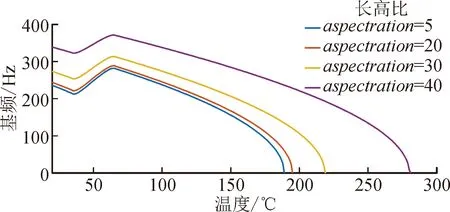
式中:EA和EM分别表示SMA在纯奥氏体和纯马氏体相时的杨氏模量。假设SMA处于文献[5]所述的零初始条件下,当温度T>As,并且CA(T-Af)<σr σr=ES(ξ)(ε-εLξS)+ΘΔT (6) 通过求解式(2)、(5)、(6)联立所得的非线性方程组,即可获得温度变化时SMA的恢复应力与马氏体体积分数,如图1所示。 图1 温度变化时SMA恢复应力与马氏体体积分数Fig.1 Recovery stress and volume fraction of martensite under temperature change 由图1可知,温度低于奥氏体开始温度时,马氏体体积分数为定值。随着温度逐渐升高,图1(a)中显示SMA恢复应力有上升的趋势,而图1(b)中马氏体体积分数是下降的,直至温度达到某个值时,SMA中将不再含有马氏体成分,变为纯奥氏体,此时,SMA恢复应力曲线的上升趋势变缓。此外,当初始应变增大时,转变为纯奥氏体的临界温度也随之增大。 SMA丝和石墨纤维内嵌在不同的环氧树脂基底层中。做旋转运动SMA层合梁示意图,如图2所示。其中,惯性坐标系为OXYZ,中心刚体的附体坐标系为O1X1Y1Z1,SMA层合梁的附体坐标系为O2X2Y2Z2。中心刚体的半径为R,层合梁绕刚体中心轴线做旋转运动的角位移为φ,角速度为Ω。 SMA层合梁的长度为L,宽度为B,总厚度为H,铺层都是等厚的,总的层数为Nl。 图2 系统简图Fig.2 System diagram 梁内任意质点P在惯性系OXYZ下的矢径为: (7) 令式(7)对时间求导,可得质点的速度为: (8) 质点任意位移与中面位移有如下关系: (9) (10) 其中,u、w是梁的中面位移,f=-z。 由式(8)、(9)、(10)可知系统的动能为: (11) 根据Von Karman大变形理论,应变为: (12) (13) 这里的f同上。 可知正应力为: (14) 应变能为: (15) 整理得内力和弯矩为: (16) 其中,NT、MT是SMA的热应力、热弯矩;Nr、Mr是SMA的恢复力、恢复弯矩。具体表达式为: 同时,等效刚度为: 在低转速的情况下,离心力不大,离心力产生的变形可忽略不计。因此,这里不考虑离心力势能。 应用Hamilton原理建立系统的动力学方程。将式(11)、(15)代入式(17)。根据Hamilton变分原理: (17) 其中,t0、t1为任意两个固定时刻。旋转SMA层合梁的运动方程为: (18) (19) 具体化简过程见附录2。 其中广义惯量为: 对方程进行简化,设轴向力N沿着x轴是恒定的[4],即: (20) 可知 (21) 经过相应的积分运算可知: (22) (23) (24) 又简支-简支梁的边界条件为:u(0,t)=0,u(L,t)=0,u′′(0,t)=0,u′′(L,t)=0。 将边界条件代入式(24),可得: (25) (26) 将式(25)、(26)回代入式(24)、(19),则系统方程可化简为单自由度运动方程: (27) 系统的振动方程整理为: (28) 可知,系统简化后是一个非线性方程。非线性系统固有频率的求解有很多种方法,比如谐波平衡法、Ritz法等。 使用振动分析中常用的Ritz法进行求解[23],设横向中面位移为: w(x,t)=aW(x)cos(ωt) (29) (30) 将式(29)代入式(30)中,经过运算,可得: (31) 由于层合材料的铺层沿中性面是对称布置的,故等效惯量I1=0,式(31)可整理为: (32) 构建方程如下: (33) 其系数为: 式(33)为四阶微分方程,其通解为: (34) 式(34)中系数表达式为: 其中,W(x)满足简支-简支梁边界条件:W(0)=0,W(L)=0,W″(0)=0,W″(L)=0。由边界条件可以得到关于系数的等式关系,并且由等式系数行列式为零,可得模态函数为: W=C4sin(nπx) (35) (36) 其中,Ω为稳定旋转角速度。计算上式即可获得固有频率。从非线性固有频率的表达式可知,由于广义惯量I2的值很小,故在低转速的情况下,大范围旋转运动对系统固有频率的影响不大。 层合梁的长度L=1 m,宽度B=0.1 m,厚度H=0.01 m,每一铺层的厚度均相等。SMA的相关参数如表1所示,石墨/环氧树脂铺层的物理参数如表2所示。层合梁的铺层为8层,纤维丝铺层沿中性面对称布置,铺层与坐标正方向夹角为[0°SMA/90°graphite/90°graphite/90°graphite],铺层是等厚的。初始情况下,ξT0=0,T0=20 ℃,SMA的初始应力σ0=0,ε0=0.2%,VS=3%。 表1 SMA参数Tab.1 SMA parameters 表2 石墨/环氧树脂铺层的物理参数Tab.2 Physical parameters of graphite / epoxy resin layer 求解式(36)可得不同角速度时的基频,如图3所示。由图3可知,在其他条件不变的情况下,转速增大时,系统的基频减小,但是不同转速下基频的变化趋势是一致的。 图3 不同角速度时的基频Fig.3 Fundamental frequency at different angular velocities 即随着温度上升,SMA转变为非晶马氏体时,基频下降;温度继续上升,SMA转变为马氏体时,基频上升。在SMA转变为纯奥氏体的过渡阶段,温度持续上升,热应力增加快于SMA的恢复应力,导致层合梁刚度减小,基频也随之减小。由图可知,SMA转变为纯奥氏体的相变温度为74 ℃,且不随旋转角速度的变化而变化。 图4是不同初始应变时基频的变化曲线。此时,设SMA层合梁的旋转角速度恒定,Ω=40 rad·s-1。研究不同初始应变下基频随温度的变化趋势。 图4 不同SMA初始应变时的基频Fig.4 Fundamental frequency of SMA with different initial strains 图4表明,当温度高于奥氏体起始温度34.5 ℃时,SMA产生的拉力变大,从而显著增加了梁的刚度,导致基频增加。奥氏体温度结束之后,温度升高对梁的膨胀作用大于SMA恢复应力的收缩作用,因此基频降低。初始应变的增大可以显著增加转变为纯奥氏体的温度,最大的转变温度为101 ℃。 图5是SMA体积分数对基频的影响曲线。 图5 不同SMA体积分数时的基频Fig.5 Fundamental frequency of SMA with different volume fractions 当SMA丝的体积分数变大时,基频的变化幅度更加显著,即基频曲线切线的斜率更大;而且,所有的基频变化曲线都经过了(49,223)这个点,该点处的横坐标为奥氏体结束温度。并且,不同体积分数下,SMA转变为纯奥氏体的温度是相同的,均为68 ℃。 研究石墨纤维铺设角度对自由振动的影响,如图6所示。此时,转速仍然为40 rad/s,SMA丝的铺设角度为定值0 °,温度为50 ℃。由图可知,初始应变越大,系统固有频率越大。 图6 石墨纤维铺设角度对基频的影响Fig.6 Influence of laying angle of graphite fiber on fundamental frequency 图6显示,不同的初始应变下,基频的变化趋势是相同的,都是随着角度的增加,基频先减小后增大。 由图7可知,随着温度上升,基频整体呈现出减小的趋势。 图7 SMA所在层对基频的影响Fig.7 Influence of SMA layer ordinal on fundamental frequency 当记忆合金所在的铺层靠近中性面时,系统的基频比SMA层位于外层时要大。这是由于记忆合金层位于内层时系统的刚度上升所致,而且SMA越靠近内层,基频的变化趋势就越缓慢。 在进行相关仿真时,除了长高比之外,其他参数如转速等,是固定不变的。由图8可知,随着温度的上升,基频整体呈现出减小的趋势。 图8 长高比对基频的影响Fig.8 Influence of aspect ratio on fundamental frequency 长高比增大时,层合梁的固有频率是增大的。这是因为,厚度是不变的,而长度是厚度的整数倍,长度增加就使得广义惯量的增幅比刚度的增幅小。 利用Hamilton变分原理,建立了大范围旋转运动SMA层合梁的动力学方程,研究了该系统的自由振动特性。 1) 在旋转角速度一定的情况下,当系统处于马氏体相变的阶段时,系统的基频随着温度的上升而增大,这是因为在该阶段SMA恢复应力急剧增大,使得系统刚度增大所致。 2) 旋转角速度增大时,基频是减小的,但是旋转运动对基频的影响有限。 3) SMA铺设角度不变而石墨纤维的角度变化时,固有频率先减小后增大。 4) SMA铺层靠近中性面时,系统刚度增大、固有频率减小,随着温度增加,基频更快地衰减为零。 5) 层合梁的长高比增大时,基频是增大的。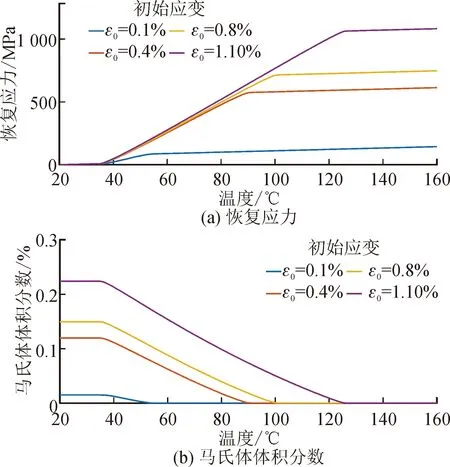
1.2 系统的动能和应变能

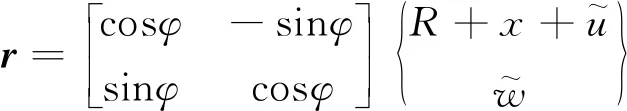



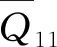
1.3 动力学方程
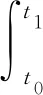
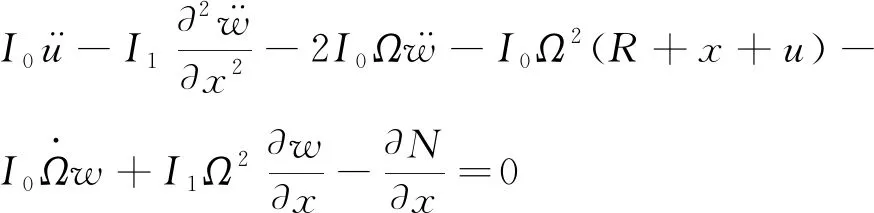
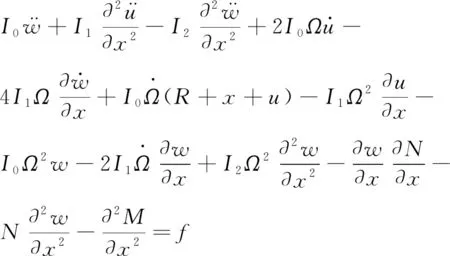
2 振动分析


3 数值计算


4 结 论

