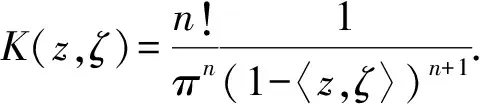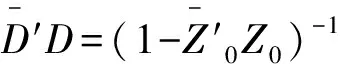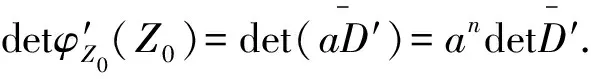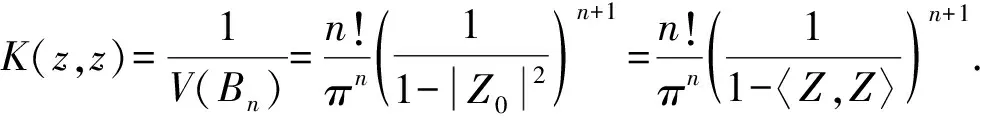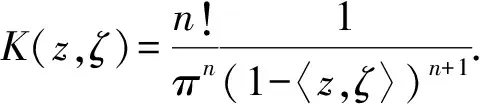单位球Bn的Bergman核函数

孙东爽

(吉林师范大学 数学学院，吉林 四平 136000)

0 引言

Bergman核函数是基于这样一个思想：复空间的有界域中的平方可积全纯函数形成了一个Hilbert空间，且Hilbert空间具有一个再生核，这是一个积分核，它再现了空间中的每个元素.Bergman核具有很多非常好的性质，在偏微分方程、函数理论、微分几何等方面有着重要的作用(对于Bergman核更深入的讨论，可以参见[1]).Bergman核是研究各类数学问题的重要分析工具，例如：陆启铿在[2]中利用Bergman核将多复变数函数论与复几何联系起来；Charles Fefferman在[3]中利用Bergman核与Bergman度量研究了双全纯映射的边界问题；Klas Diederich与Gregor Herbort在[4]中研究了Bergman度量与Green函数问题等.因此得到各类域的Bergman核显式表达式是十分重要的.在文献[5]中介绍了利用完备规范正交系或者利用域的全纯自同构求Bergman核函数的方法；在文献[6]中介绍了典型域的Bergman核函数，特别地，m=1时，第一类典型域RI(m,n)是单位球Bn.本文综述了单位球Bn的Bergman核函数三种计算方法.证法一利用完备规范正交系进行计算；证法二利用单位球Bn是可递圆型域，计算自同构群元素Jacobi矩阵的行列式来求出Bergman核；证法三利用第一类典型域的Bergman函数的计算方法得出结论.下面给出单位球Bn的Bergman核函数详细过程.

1 单位球Bn及其自同构群

定义1[7]以a=(a1,a2,…,an)∈n为中心，ρ>0为半径的球是指

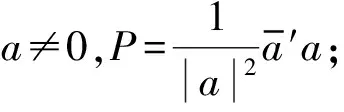
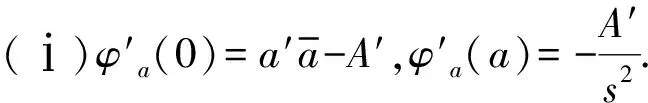
(ⅱ)φa∈Aut(Bn).

2 Bergman核函数

定义2[5]设Ω是n中的有界域，{φk}是(L2∩H)(Ω)中一组完备的规范正交系，称是Ω的Bergman核函数.

下面给出可递域和圆型域的定义，进而得出单位球Bn是可递的圆型域.

定义3[7]设Ω⊂n为区域.若对任意两点p,q∈Ω，一定存在φ∈Aut(Ω)，使得φ(p)=q，则称Ω为可递域或齐性域.

引理[7]单位球Bn是可递域.

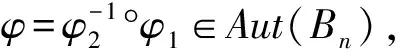
定义4[7]设D⊂n是有界域.若∀z∈D,θ∈R，有eiθz∈D，就称D是有界圆型域.

显然单位球Bn是圆型域.事实上，任取z=(z1,…,zn)∈Bn，则有|z1|2+…+|zn|2<1.任取实数θ，则有|eiθz|2=|eiθz1|2+…+|eiθzn|2=|eiθ|2[|z1|2+…+|zn|2]<1.

定理2[5]设Ω是n中的有界域，

定理3[5]设Ω是n中的有界域，Ω的核函数K(z,ζ)由K(z,z)所唯一确定.

3 第一类典型域

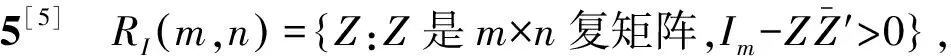
由于当m=1时，RI(m,n)就是单位球，所以可以得到如下结论：

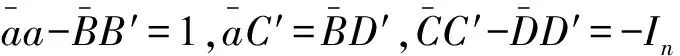
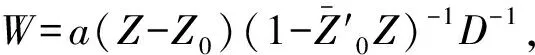
4 单位球Bn的Bergman核函数的计算

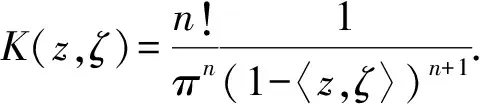
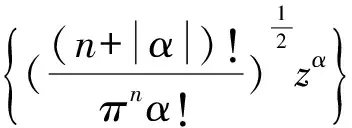
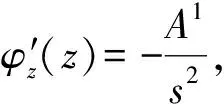
现在对矩阵A进行矩阵变换

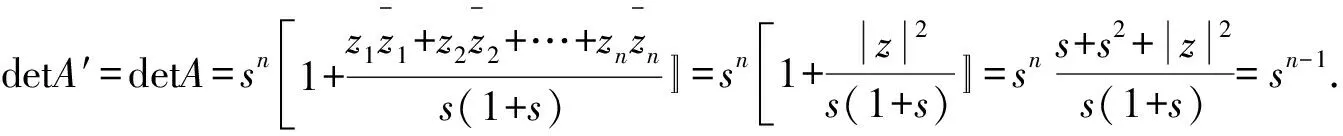
又因为单位球Bn是有界域，所以单位球Bn的Bergman核函数K(z,ζ)是由K(z,z)唯一决定的.