面向用户及评分信息的混合数据聚类推荐算法

邹伟静，庞天杰

(太原师范学院 计算机系，山西 晋中 030619)

0 引言

在互联网的高速发展的今天，网络信息的增长速度呈现爆炸式增长.大数据的时代背景下，每天新增的数据量字节数已经达到了1018量级，该数据量远远超出了人们能接受的范围，互联网出现了信息过载的情况.面对互联网上数量如此庞大的信息，人们会不知所措，不知道如何从中快速地获取自己需要的信息.针对信息过载现象，如何快速地解决该问题成为了一个热点话题.解决信息过载问题的手段有很多，推荐算法就是其中最有效的手段之一，并在各个领域得到了广泛应用，如电影、购物等等.但是随着用户和商品的规模不断扩大，信息变得越来越稀疏，这是推荐算法面临的主要问题之一[1-4].比如在一些购物网站，总商品数量有数以百万计，但是用户买过的商品数量微乎其微，再加上许多用户并不会对商品进行评分和评价，这就导致了用户评分信息矩阵极其稀疏.在实际的用户数据中，不仅有用户的历史行为数据，而且包括用户自身的分类属性.因此用户数据是一种既有评分数据又有属性数据的混合数据.然而在面对用户数据时，传统的推荐算法往往并没有充分挖掘用户信息，只取了用户的评分数据作为相似度计算的依据，这就使得对用户信息挖掘不充分，导致实际推荐算法效果不佳.

为了解决推荐算法的数据稀疏的问题，聚类算法是十分有效的方法之一.因此许多学者采用聚类的手段来改进推荐算法.文献[5]通过挖掘用户的特征信息来改进相似度的计算,并用改进的聚类算法对用户进行聚类.文献[6]采用FCM对用户进行聚类，并采用遗传算法对聚类算法进行改进防止出现局部最优解，最后用实验结果证明了改进算法的有效性.文献[7]首先利用谱聚类对用户进行聚类分组，再基于聚类对评分矩阵进行降维，最后基于隐语义模型对用户进行评分预测.文献[8]采用半监督密度峰值聚类算法将用户按兴趣分组，并结合社交网络关系建立用户的信任集合，最后为目标用户实现协同过滤推荐.

上述文章中的算法一定程度上提高了推荐系统的预测准确性，但是对于用户信息挖掘不够充分，因为在实际生活中，用户数据往往是既有评分数据又有属性数据的混合数据，在挖掘用户信息的时候需要从混合数据入手.为了解决该问题，提出了一种面向用户及评分信息的混合数据聚类推荐算法，旨在分析用户的混合数据来提升推荐质量.首先通过分析用户的混合数据，计算出用户在混合数据上的相似度；然后采用聚类算法对用户进行聚类并得到多个聚类簇.最后在聚类簇中对目标用户实现协同过滤推荐.

1 传统的基于聚类的协同过滤推荐算法

传统的基于聚类的协同过滤推荐算法的基本流程如下：首先利用用户历史数据，构建出用户-物品评分矩阵；之后采用聚类算法对用户进行聚类，得到关于用户的聚类簇；然后在一个聚类簇中计算用户间的相似度，并利用协同过滤思想为目标用户进行评分预测；最后根据预测结果依照Top-N原则对目标用户进行推荐[9].

1.1 构建矩阵

用户-物品评分数据中有m个用户和n个物品.根据数据构建出用户-物品评分矩阵Rm×n.rij表示用户i对物品j的评分，若用户i对物品j未评分，则rij记为0.由此可以构建出用户-物品评分矩阵：

1.2 距离和相似度的度量

根据得到用户-物品评分矩阵，获得每个用户的评分向量.将用户评分向量之间的距离和相似度作为用户间的距离和相似度.常见的距离和相似度度量[10]公式如下.

1.2.1 欧式距离

欧式距离是最为常见的度量样本间距离方法之一.用户间的欧式距离计算公式如下：

(1)

(1)式中，D(u,v)表示用户u和用户v间的欧式距离，rui和rvi分别表示用户u和用户v对第i个物品的评分，n表示物品总数.

1.2.2 皮尔森相关系数

距离度量可以用相关系数来表示[10].用户间的皮尔森相关系数计算公式如下：

(2)

1.3 用户聚类

利用上文的距离公式对用户进行聚类，在聚类算法的选取上，以较为常用K-means++聚类算法为例.聚类算法步骤如下：

步骤1 从样本集U中随机选取一个点c1作为初始聚类中心；

步骤2 遍历U中的样本点，得到当前样本点和所有聚类中心最近的距离dx；

步骤3 用(3)式计算每一个样本点作为下一个聚类中心的概率；

(3)

步骤4 根据轮盘赌算法选出下一个聚类中心ci；

步骤5 重复步骤2-步骤4，直至找到k个初始聚类中心；

步骤6 利用K-means算法步骤得到k个聚类簇.

1.4 预测评分

有了上文的k个聚类簇，在当前聚类簇中选取h个与目标用户最为相似的用户并作为该用户的近邻集，用评分预测公式为目标用户进行评分预测，预测公式如下：

(4)

(4)式中，pai表示用户a对物品i的预测评分，G表示用户a的近邻集.

2 混合数据聚类推荐算法HDCRA

在实际的数据当中，用户不仅有评分数据，还有其自身的属性数据，这两种数据往往是在一起的，构成了用户的混合数据.对于该混合数据，不同部分需要做不同处理并加以结合，本文对用户之间的相似度计算进行了重新定义.此外大数据数据量大的特点导致了数据的稀疏性，采用聚类算法对用户进行聚类来达到降低数据稀疏的效果，将相似的用户划分到一个聚类簇中，从而提高推荐算法的准确性.

2.1 相似度计算

根据上文的分析，在计算用户之间的相似度时，只用评分对用户进行相似度的计算并不能将用户划分清晰.因此要计算用户的混合数据之间的相似度.混合数据由属性数据和评分数据构成，对这两部分的相似度方法如下.

从“十八大”以后中央特别注重我国的环境建设。汽车维修过程中会产生一系列排放物，从环保角度讲，首先要做的是识别，识别出哪些是污染物，哪些是正常的排放物。汽修行业中，污染物分为三类，分别是液体、固态物和气体。

2.1.1 属性数据

对于属性数据的处理，采用如下公式计算用户之间的属性相似度：

(5)

(5)式中，sim_a(u,v)表示用户u和用户v在属性a上的相似度，ua和va分别表示用户u和用户v在属性a上的值.

如用户的年龄属性特征，由埃里克森八阶段理论[11]可知，人的心理社会发展随着成长而发生变化，一共要经历八个阶段.于是在数据集中便根据用户年龄处在的不同阶段对用户年龄进行编码，以此将不同年龄的用户划分到对应的心理社会年龄段中.因此可以得到用户u和用户v的年龄属性特征相似度计算公式：

(6)

(6)式中，au为用户u的年龄编码；av为用户v的年龄编码.

2.1.2 评分数据

对于评分数据的处理，一般采用最为常用且效果好的皮尔森相关系数计算用户间的相似度.

此外在物品集中，大家对热门物品的关注度不尽相同，但是对于冷门物品，一般只有相似的人才会关注，因此在评分相似度中加入对热门物品的惩罚系数[12]，惩罚系数如下：

(7)

式中，|D(i)|表示物品i的流行度.

将该惩罚系数融入评分相似度得到如下评分相似度计算公式：

(8)

将用户的属性数据特征相似度与评分数据特征相似度融合，得到一种新的相似度计算模型，即用户的混合数据特征相似度计算模型，公式如下：

(9)

(8)式中，sim_A(u,v)表示用户u和用户v各个维度的属性相似度的和，|·|表示用户属性特征和评分特征的维度.

2.2 基于K-means++的用户聚类

得到了用户的相似度后，需要对用户进行聚类.K-means++算法是进行聚类时最常用的算法之一[13].其基于K-means算法并在聚类中心的选择上做了优化，在选择聚类中心时，使得聚类中心尽可能远，达到高内聚低耦合的效果.相比于K-means算法，K-means++算法具有稳定高效的特点，本文采用K-means++算法作为用户聚类手段.算法步骤如下：

步骤1 从样本集U中随机选取一个点c1作为初始聚类中心；

步骤2 遍历U中的样本点，得到当前样本点与所有聚类中心最大的相似度sx；

步骤3 根据公式计算每一个样本点作为下一个聚类中心的概率；

(10)

步骤4 根据轮盘法选出下一个聚类中心ci；

步骤5 重复步骤2-步骤4，直至找到k个聚类中心；

步骤6 将剩余样本点划分到最为相似的一类中并得到k个聚类簇.

最后根据聚类结果预测出用户对物品的评分，公式如下所示：

(11)

(11)式中，pai表示用户a对物品i的预测评分，G表示用户a的近邻集.

3 实验与讨论

3.1 实验数据

实验数据选取的是MovieLens ml-100k电影数据集[14].该数据集包括用户评分数据集和用户属性数据集，属于上文提到过的混合数据类型.用户评分数据集是由943名用户对1 682部电影评分共约10万条评分数据构成，每个用户对电影的评分为1-5分.用户属性数据集包含了用户的种种属性，如年龄、性别等.实验采用五折交叉实验法验证算法的有效性，取五次实验的平均结果作为实验的最终结果.

3.2 评价指标

实验将采用平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Square Error，RMSE)作为评价指标[15].评价指标的公式如下：

(12)

(13)

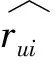
3.3 实验结果与分析

由于K-means++算法需设定聚类数目k，为了能有良好的推荐效果，本文先设置聚类数目区间为[5,50]，增量为5.通过轮廓系数[16]来衡量聚类效果.实验结果表1所示.

表1 不同聚类数目k下的轮廓系数

由于算法是基于相似度聚类，因此轮廓系数越低聚类效果越好，根据实验结果可得出结论，在聚类数目k=35时轮廓系数最低，因此将聚类数目设定为35.

为了验证提出的推荐算法HDCRA的有效性.将本文算法与传统的基于用户的协同过滤推荐算法(User-based CollaboratIve Filtering，User-CF)和用户聚类算法(K-means User Clustering，KUC)进行比较，并采用上文所述指标进行对实验结果进行分析评价.MAE实验结果如图1所示.

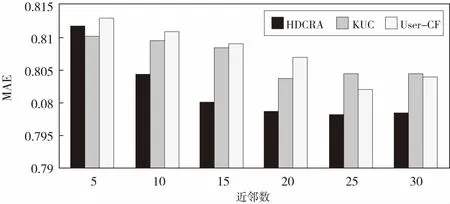
图1 不同算法下的MAE值对比

由图1可以看出，三种算法的MAE在实验数据集上的表现均随着近邻数的增大而减少且趋势逐渐平缓.在近邻数相同的情况下，HDCRA的MAE值整体上低于User-CF算法和KUC算法，说明HDCRA在推荐的精度上要优于User-CF算法和KUC算法.RMSE的实验结果如图2所示.

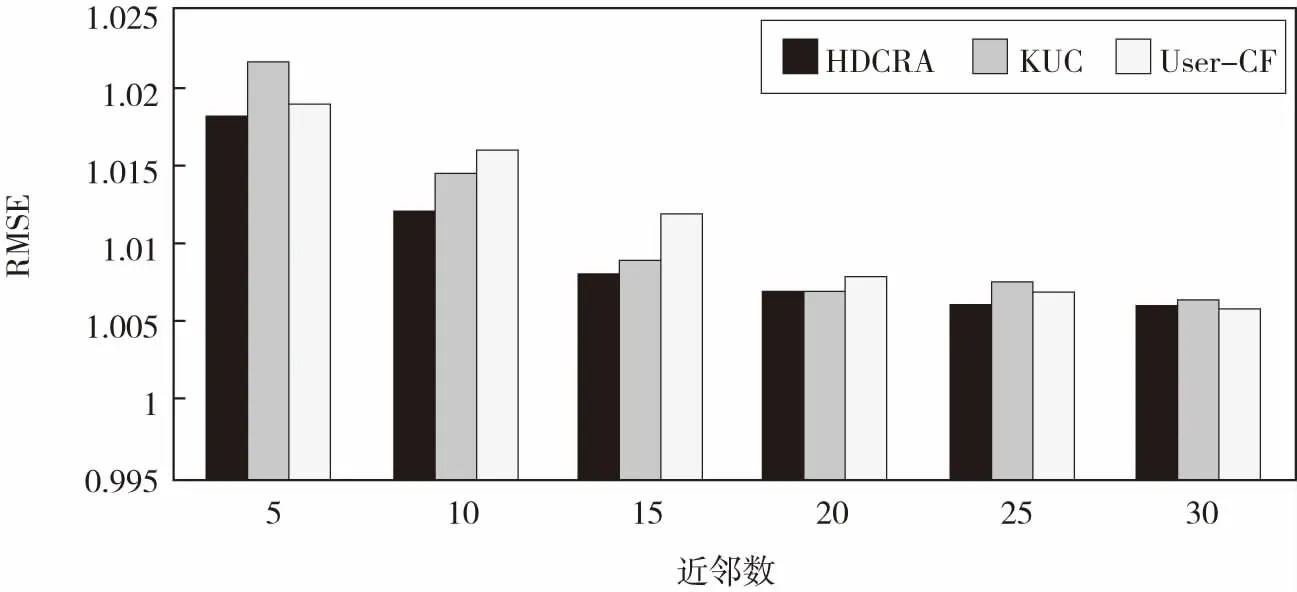
图2 不同算法下的RMSE值对比

由图2可以看出，三种算法的RMAE在实验数据集上的表现均随着近邻数的增大而减少且趋势逐渐平缓.在近邻数相同的情况下，HDCRA的实验结果在整体上要低于User-CF算法和KUC算法，进一步说明HDCRA在推荐的效果上要优于User-CF算法和KUC算法.

4 结语

本文针对推荐算法面对的数据稀疏性和推荐质量不佳的问题，根据实际用户数据是一类既有评分数据和属性数据的混合数据，提出了一种面向用户及评分信息的混合数据聚类推荐算法HDCRA.根据算法在实验中的表现发现，该算法优于传统的推荐算法，弥补了传统推荐算法的不足，在推荐精度和推荐质量上都存在一定优势，进一步验证了该算法的有效性.