传递函数辨识(26):方程误差自回归滑动平均系统的递阶广义增广迭代参数估计
丁 锋,徐 玲,籍 艳,刘喜梅
(1.江南大学 物联网工程学院,江苏 无锡 214122;2.青岛科技大学 自动化与电子工程学院,山东 青岛 266061)
方程误差自回归滑动平均模型(equation-error ARMA model,EEARMA模型)是方程误差类模型的最一般形式。它的特例有方程误差滑动平均模型(equation-err or moving average model,EEMA模型),方程误差自回归模型(equation-err or autoregressive model,EEAR模型)。EEARMA模型也称为受控自回归自回归滑动平均模型(controlled autoregressive ARMA model,CARARMA模型),即受控自回归ARMA模型或受控ARARMA模型,或ARARMAX模型(即带外加输入的ARARMA模型)。
系统辨识是研究建立系统数学模型的理论与方法,高精度的数学模型是实现高精度控制的基础。最近出版的系统辨识学术专著[1-7]和连载论文[8-32]中介绍了许多系统辨识方法。最近的连载论文研究了输出误差模型的辅助模型递阶迭代参数估计方法[25]、有限脉冲响应滑动平均系统的递阶增广迭代参数估计方法[27]、线性回归系统的递阶迭代参数估计方法[29]、线性回归系统的变间隔递阶迭代参数估计方法[31]等。《系统辨识:迭代搜索原理与辨识方法》第2章研究了方程误差滑动平均系统的增广迭代辨识方法、方程误差自回归系统的广义迭代辨识方法、方程误差自回归滑动平均系统的广义增广迭代辨识方法[5]。本工作基于递阶辨识原理,研究方程误差自回归滑动平均系统的递阶广义增广迭代辨识方法。有关递阶辨识原理与方法可参见专著[7]。
1 EEARMA系统的递阶辨识模型
考虑下列方程误差自回归滑动平均模型(EEARMA模型)描述的随机控制系统,
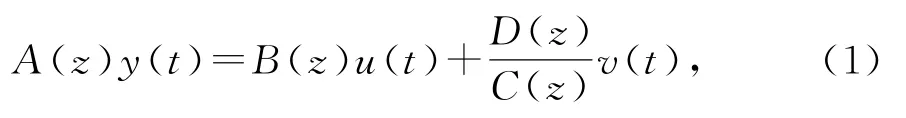
其中{u(t)}和{y(t)}分别是系统的输入和输出序列,{v(t)}是零均值不可测白噪声序列,A(z),B(z),C(z)和D(z)是后移算子z-1的多项式(z-1y(t)=y(t-1)或zy(t)=y(t+1)),定义如下,
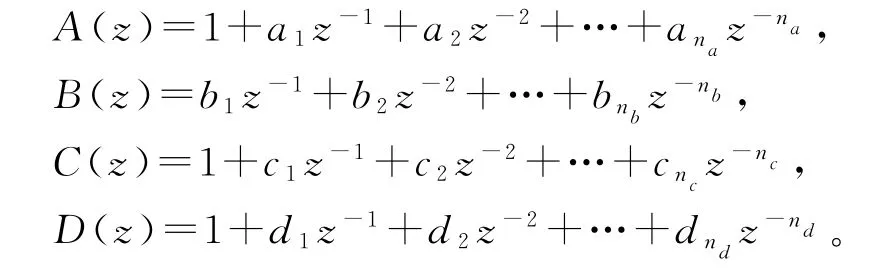
定义干扰噪声,

这里w(t)是一个ARMA噪声,是有色噪声。假设阶次na,nb,nc和nd已知,记n=na+nb+nc+nd。设t≤0时,各变量的初值为零:u(t)=0,y(t)=0,w(t)=0,v(t)=0。
定义参数向量:

和信息向量:
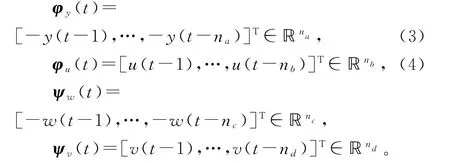
注意到输入信息向量φu(t)包含了系统输入u(t-i),输出信息向量φy(t)包含了系统输出y(t-i),它们是已知的;噪声向量ψw(t)包含了不可测相关噪声项w(t-i),噪声向量ψv(t)包含了不可测白噪声项v(t-i),它们是未知的。
由式(2)可得

定义虚拟输出变量:
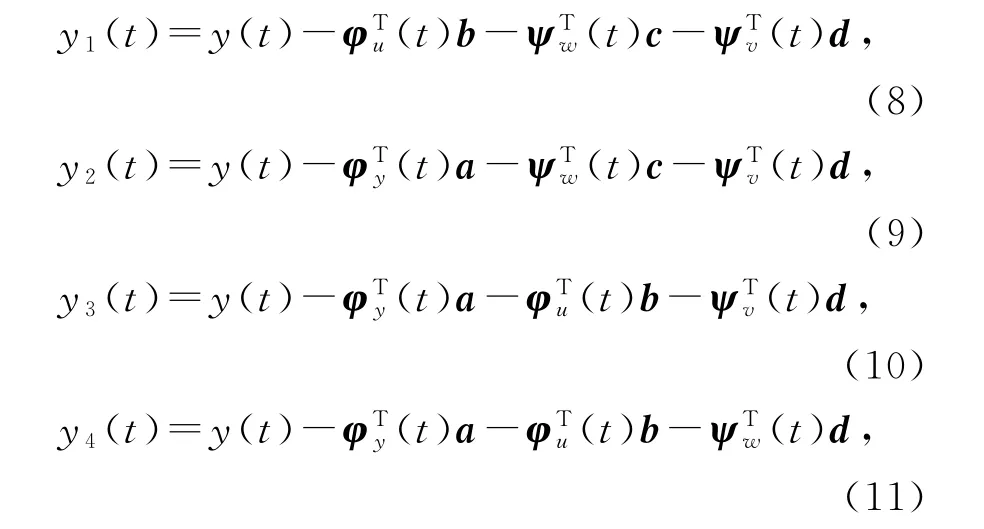
由式(7)可得4个子辨识模型:

式(12)~(15)是EEARMA系统(1)的基于模型分解得到的4个子辨识模型,即递阶辨识模型。4个子辨识模型分别包含了系统模型的参数向量a和b,以及噪声模型的参数向量c和d。
由于分解,导致4个子辨识模型间存在耦合变量(关联项)b,c,d和a。因此在推导4个子辨识算法时,需要根据递阶辨识原理,协调它们之间的关联项。基于分解的辨识方法也称为递阶辨识方法。
2 递阶广义增广梯度迭代方法
基于递阶辨识模型(12)~(15),定义4个准则函数:

令k=1,2,3,…是迭代变量和分别是参数向量a,b,c和d的第k次迭代估计,1/r1(L),1/r2(L),1/r3,k(L)和1/r4,k(L)为非负迭代步长(收敛因子),使用负梯度搜索,极小化J1(a),J2(b),J3(c)和J4(d),得到梯度迭代关系:
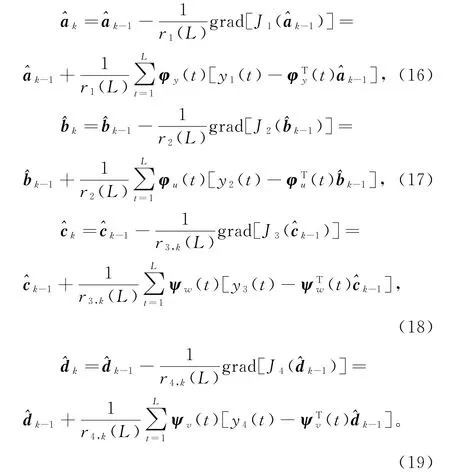
式(16)~(19)右边虚拟输出yi(t),噪声向量ψw(t)和ψv(t)是未知的,所以无法计算出参数估计和。解决的方案是,先获得yi(t),ψw(t)和ψv(t)的估计和,将辨识算法中未知量用他们的估计代替。定义式(8)~(11)中yi(t)涉及到未知参数向量b,c,d和a,以及未知噪声向量ψw(t)和ψv(t),为此用噪声w(t-i)和v(t-i)的估计和定义噪声向量ψw(t)和ψv(t)的估计:
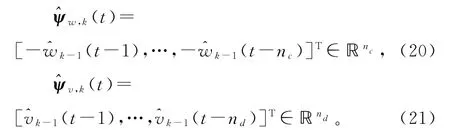
根据yi(t)的定义式(8)~(11),用参数向量b,c,d和a的前 一次迭代 估计和,以及噪声向量ψw(t)和ψv(t)的估计和定义yi(t)的估计,即
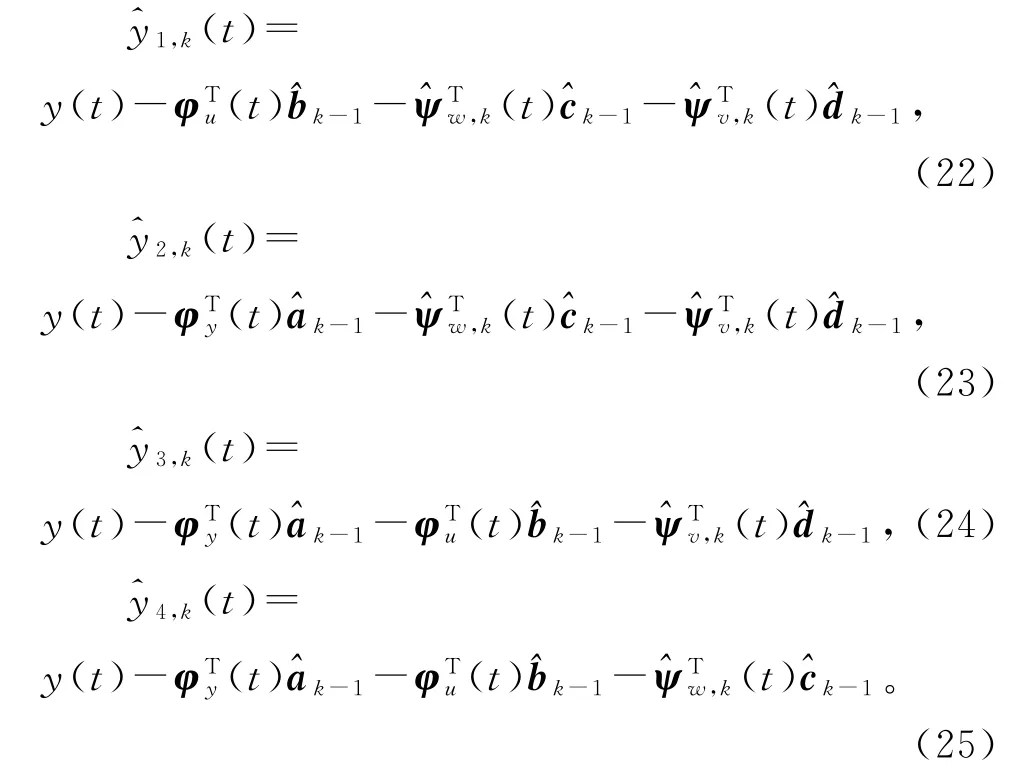


式(16)~(19)中未知的yi(t),ψw(t)和ψv(t)用其估计和代替,得到式(28)~(31),联立式(20)~(27)和(3)~(4),便得到估计参数向量a,b,c和d的递阶广义增广梯度迭代算法(hierarchical generalized extended gradientbased iterative al gorit h m,HGEGI算法):
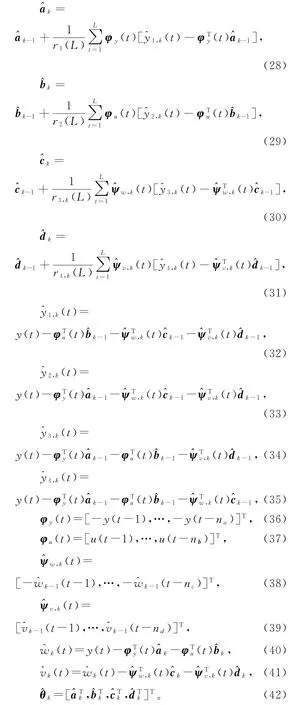
定理1对HGEGI算法(28)~(42),如果r1(L),r2(L),r3,k(L)和r4,k(L)满足

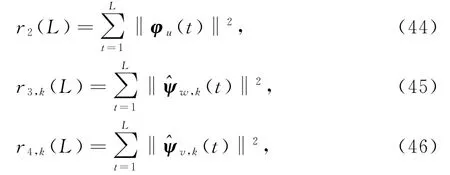
也可采用下列递推算式计算:
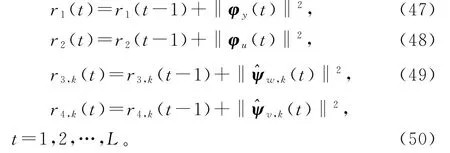
1)初始化:给定数据长度L和参数估计精度ε,置参数估计,。
2)令k=1,采集观测数据u(t)和y(t),置,…,L。用式(36)~(37)构造输出信息向量φy(t)和输入信息向量φu(t),t=1,2,…,L。根据式(43)和(44)计算r1(L)和r2(L)。
3 递阶广义增广最小二乘迭代方法
设t=l为用作辨识的数据起点,L为数据长度。基于递阶辨识模型(12)~(15),定义4个准则函数:
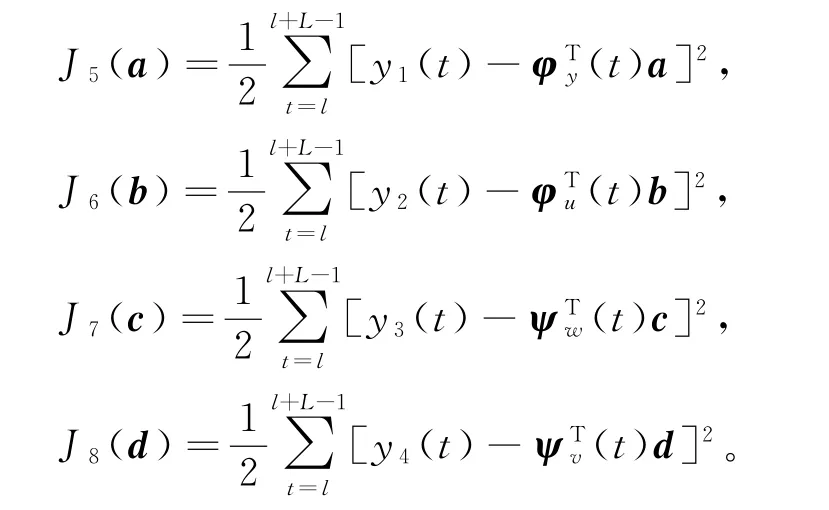
定义协方差阵Pa(L),Pb(L),Pc(L)和Pd(L)如下:
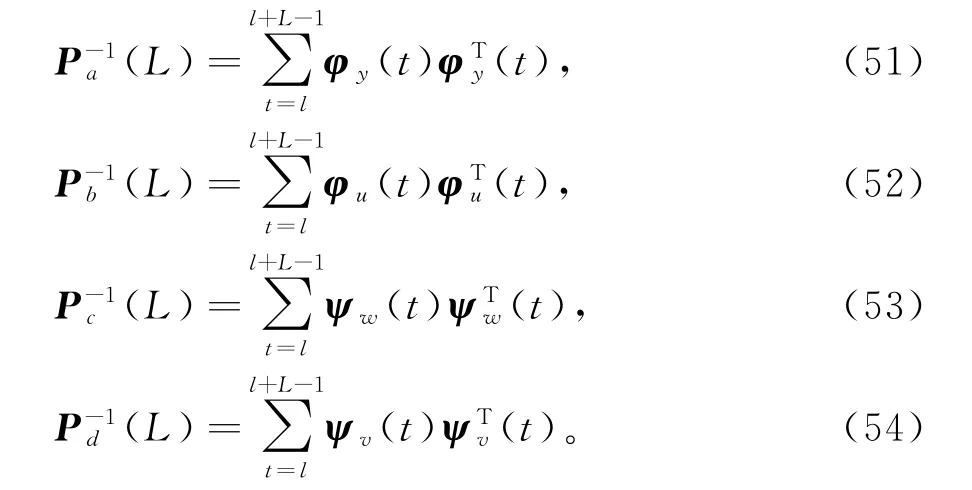
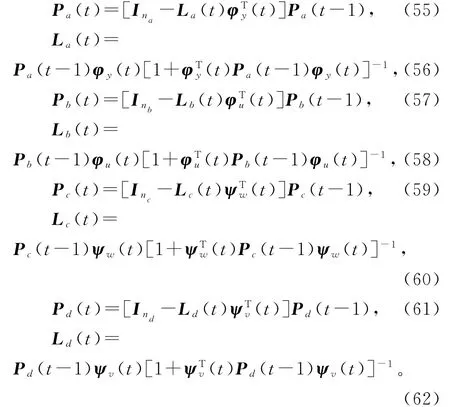
令k=1,2,3,…是迭代变量,和分别是参数向量a,b,c和d在时刻t的第k次迭代估计。令准则函数J5(a),J6(b),J7(c)和J8(d)在点,和的梯度为零,得到
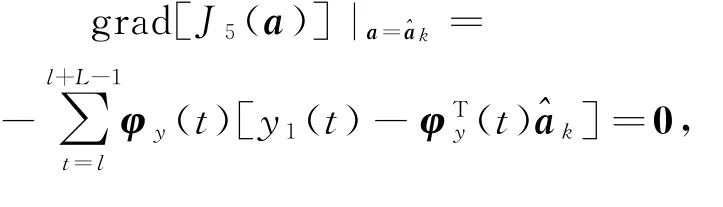
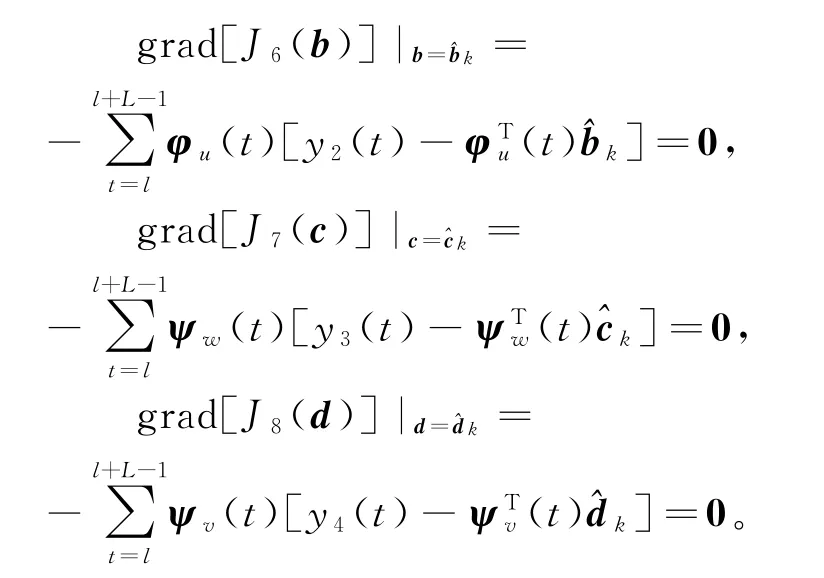
假设φy(t),φu(t),ψw(t)和ψv(t)是持续激励的,从以上4式可以求得
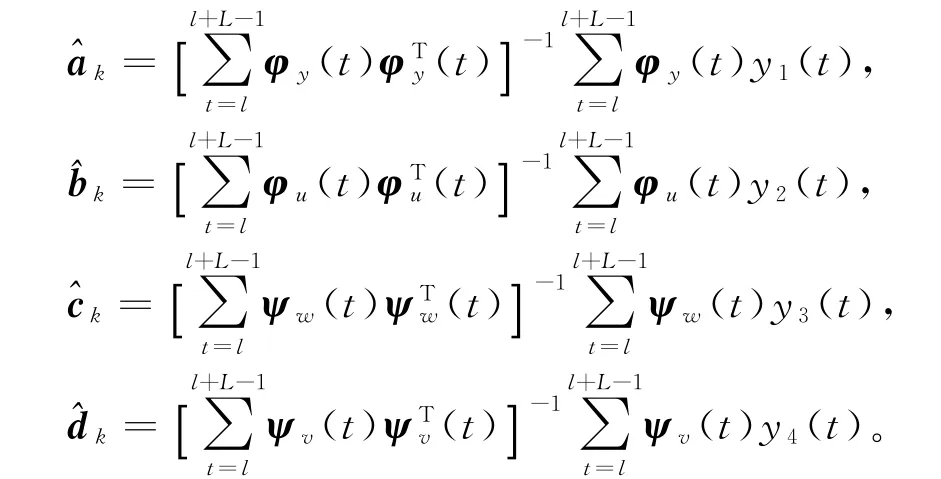
使用式(8)~(11),可得
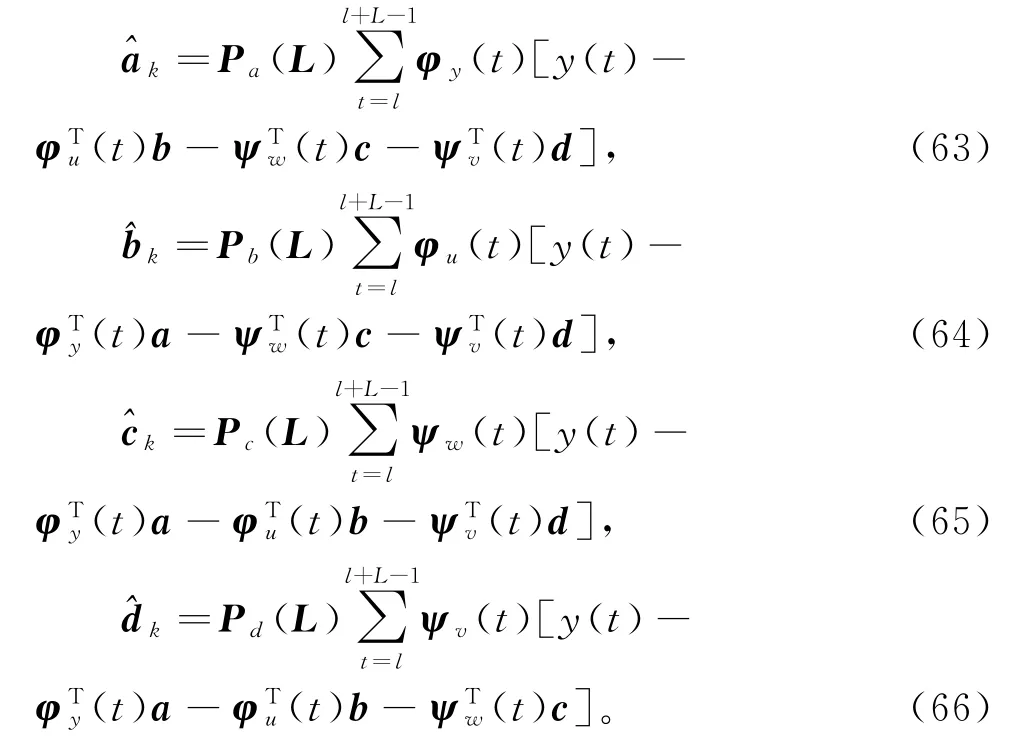

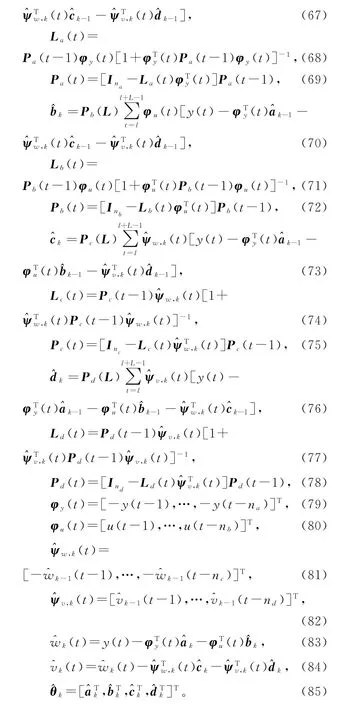
读者可以讨论引入加权因子和(或)遗忘因子的加权递阶广义增广最小二乘迭代算法(W-HGELSI算法)和遗忘因子递阶广义增广最小二乘迭代算法(FF-HGELSI算法)。
1)初始化:给定数据长度L(通常取L≫n)和参数估计精度ε,置参数估计初值,。
2)令k=1。采集输入输出数据u(t)和y(t),置,…,l+L-1。用式(79)~(80)构造输出信息向量φy(t)和输入信息向量φu(t),t=l,l+1,…,l+L-1。
5)用式(68),(71),(74)和(77)计算增益向量La(t),Lb(t),Lc(t)和Ld(t),用式(69),(72),(75)和(78)计算协方差阵Pa(t),Pb(t),Pc(t)和Pd(t)。
6)如果t<L,t就增加1,转到步骤5);否则用式(67)、(70)、(73)和(76)刷新参数估计向量,和。用式(85)构成系统的参数估计向量。
7)用式(83)和(84)计算噪声的估计^wk(t)和,t=1,2,…,l+L-1。
4 递阶多新息广义增广梯度迭代方法
基于递阶辨识模型(12)~(15),定义4个准则函数:
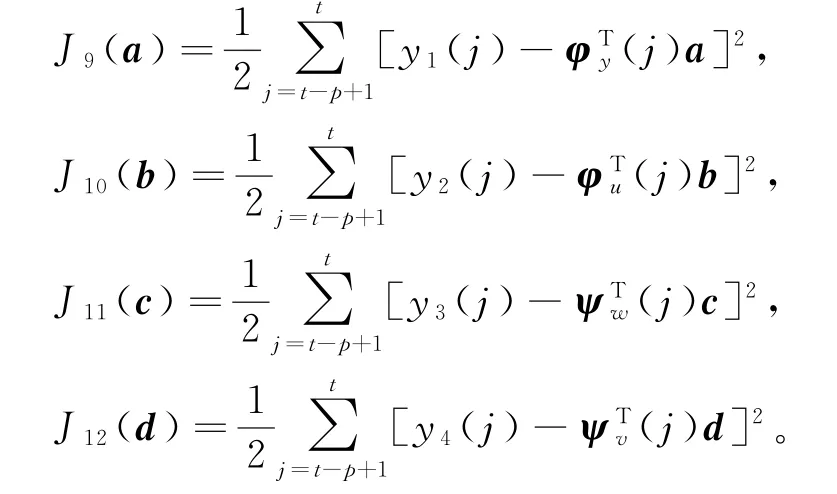
令k=1,2,3,…是迭代变量,,和分别是参数向量a,b,c和d在时刻t的第k次迭代估计,μ1(t),μ2(t),μ3(t)和μ4(t)为非负迭代步长(收敛因子),使用负梯度搜索,极小化J9(a),J10(b),J11(c)和J12(d),得到梯度迭代关系:

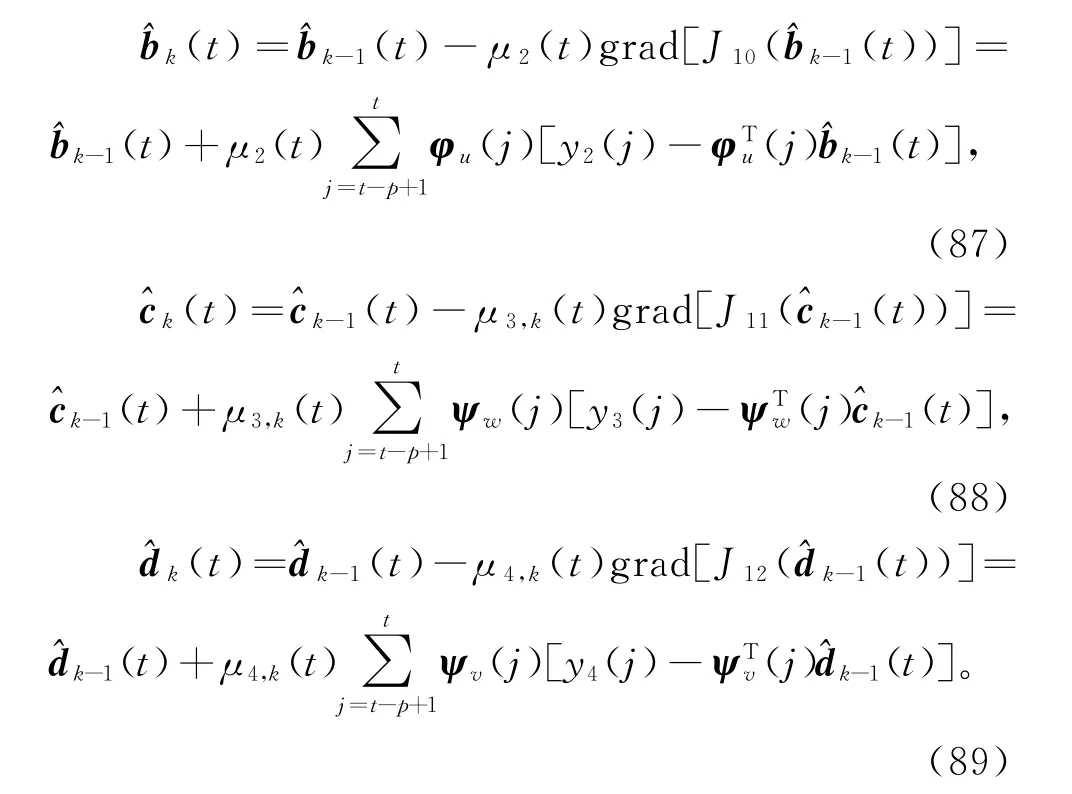
因为虚拟输出yi(t),噪声向量ψw(t)和ψv(t)是未知的,所以以上几式无法计算出参数估计,和。因此首先要获得yi(t),ψw(t)和ψv(t)的估计和)。
由yi(t)的定义式(8)~(11)可知,它们涉及到未知参数向量b,c,d和a,以及未知噪声向量ψw(t)和ψv(t)。为此用噪声w(t-i)和v(t-i)的估计和定义噪声向量ψw(t)和ψv(t)的估计:
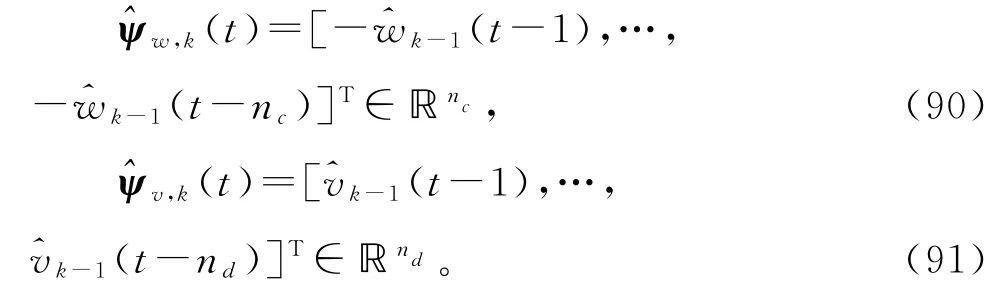
由yi(t)的定义式(8)~(11)可得

据此,用参数向量b,c,d和a的估计,和,以及噪声向量ψw(j)和ψv(j)的估计和定义估算yi(j)的辅助模型:
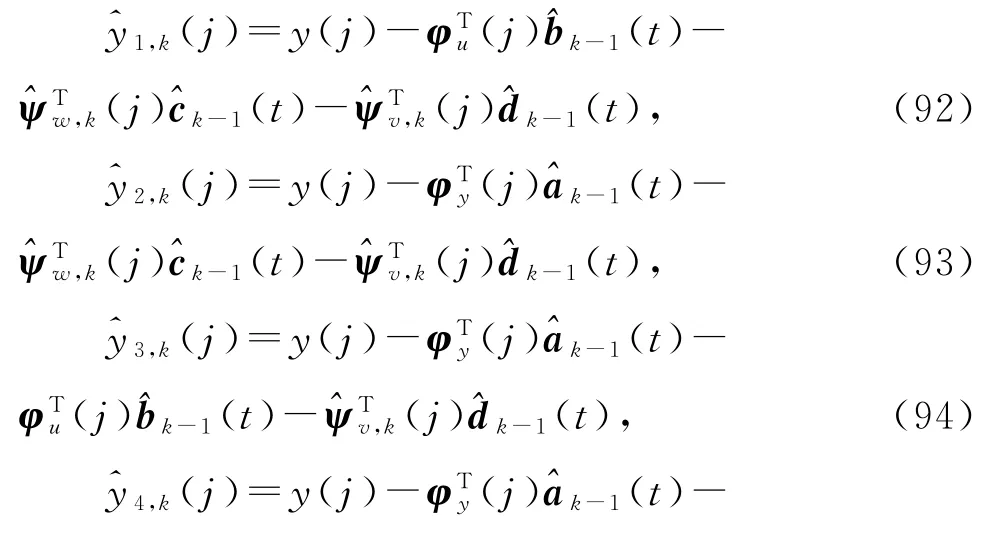
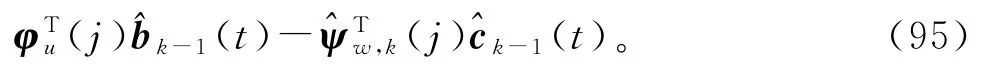
由式(6)有
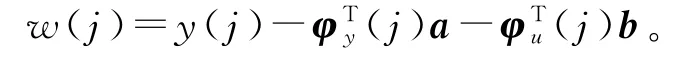
据此,用参数向量a和b的估计和,及信息向量φy(j)和φu(j)定义噪声w(j)的估计
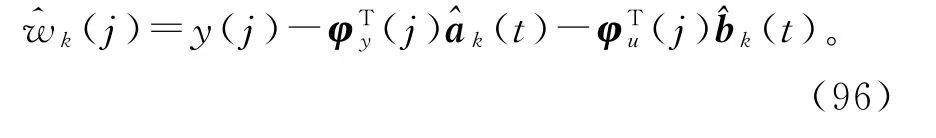
由式(5)有
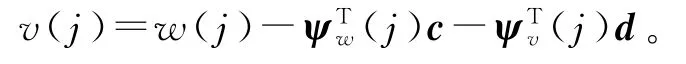
据此,用w(j)的估计^wk(j),参数向量c和d的估计和,以及信息向ψw(j)和ψv(j)的估计和定义噪声v(j)的估计
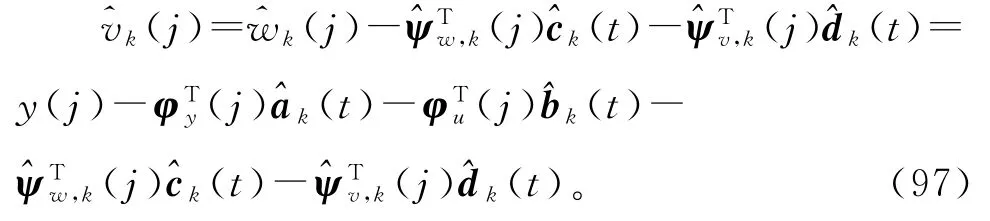
式(86)~(89)中未知的yi(j),ψw(j)和ψv(j)用其估计和代替,得到式(98)~(101),联立式(90)~(97)和(3)~(4),便得到估计参数向量a,b,c和d的递阶多新息广义增广梯度迭代算法(hierarchical multi-innovation generalized extended gradient-based iterative algorith m,HMI-GEGI算法):
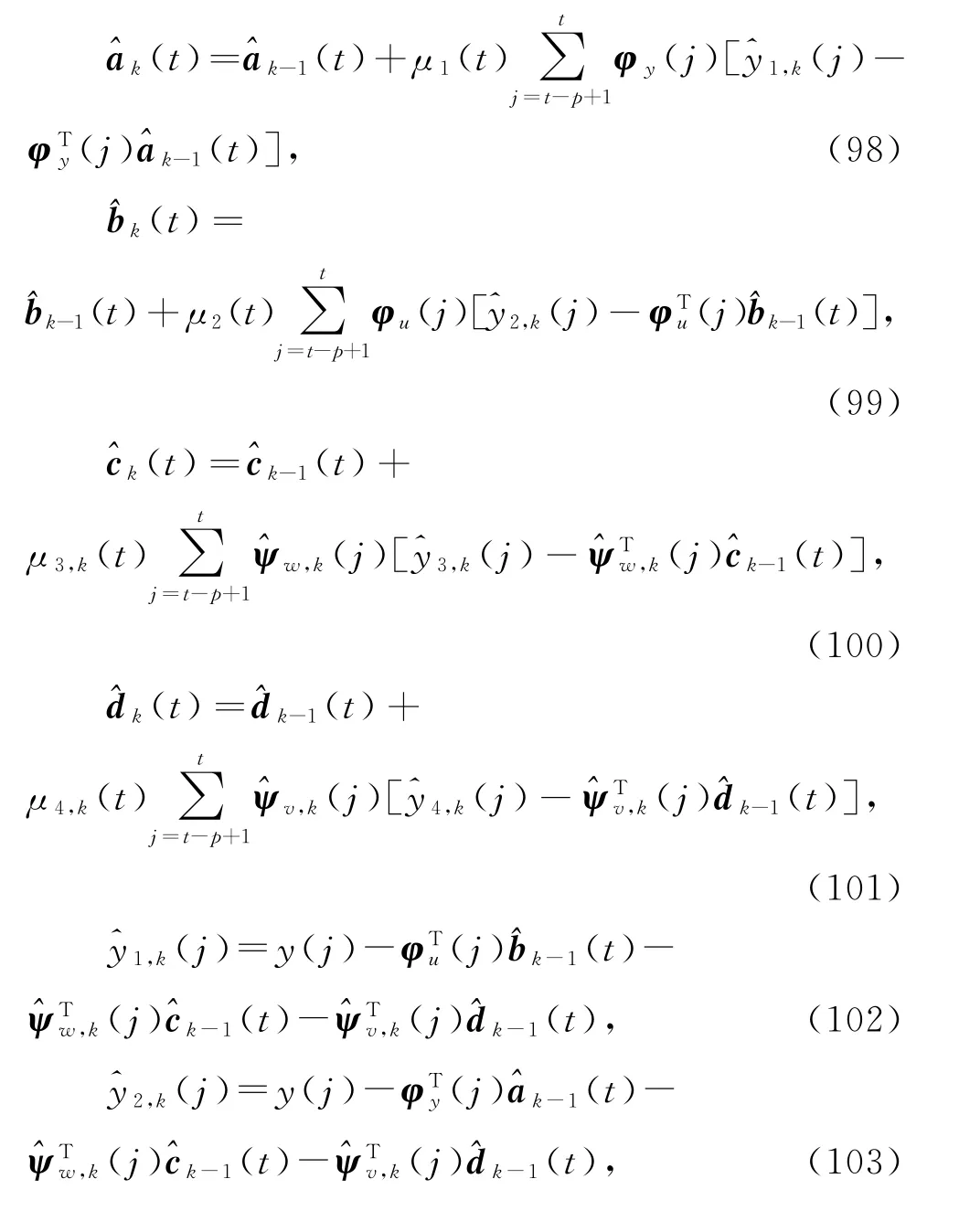
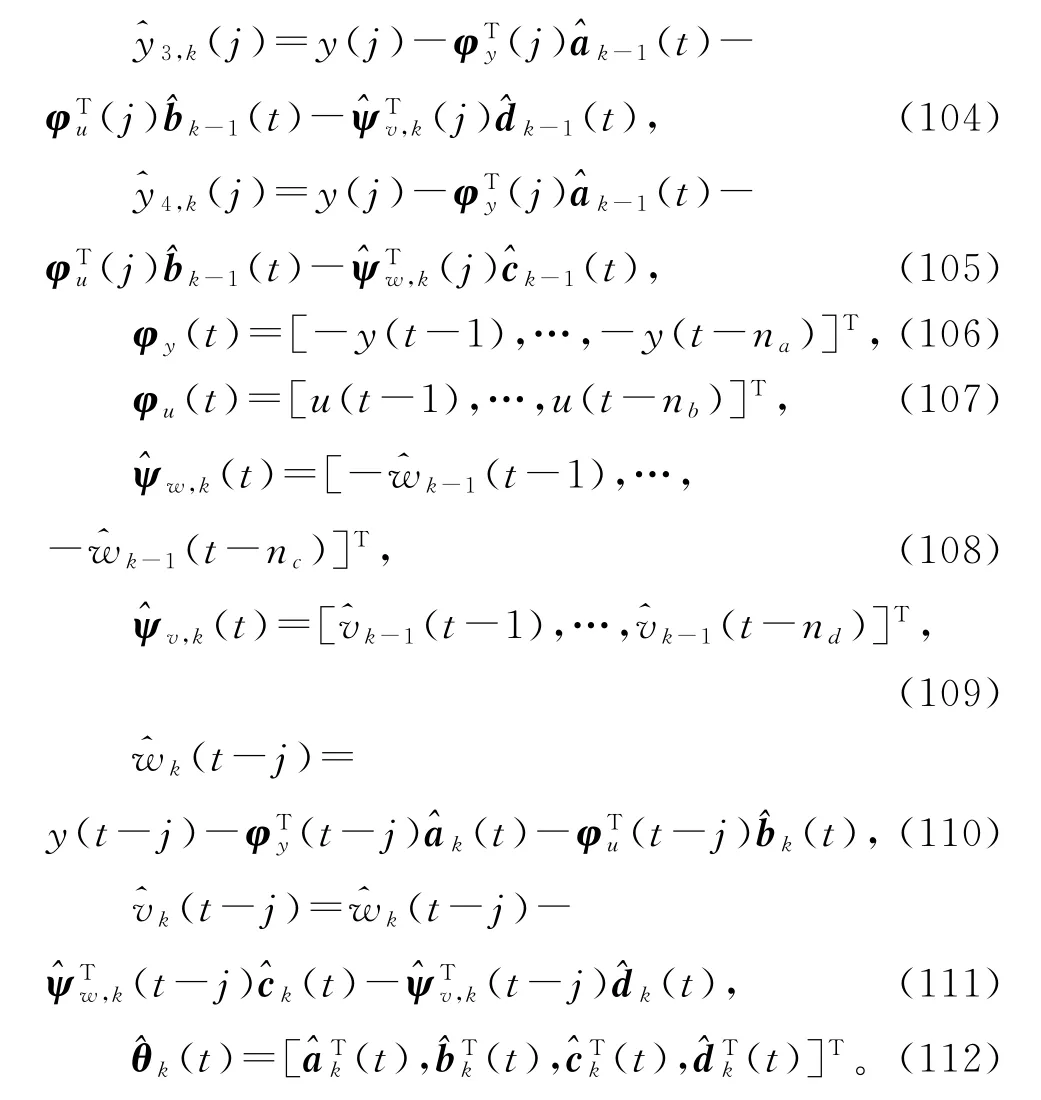
定义新息
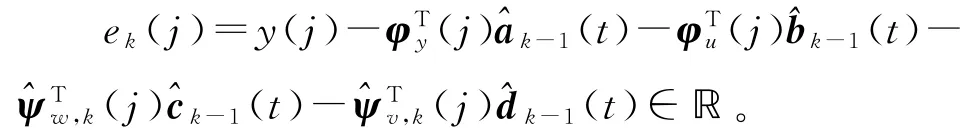
定理2对H MI-GEGI算法(98)~(112),如果收敛因子满足

为简化计算,步长也可取为
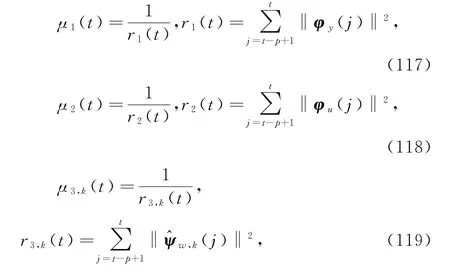
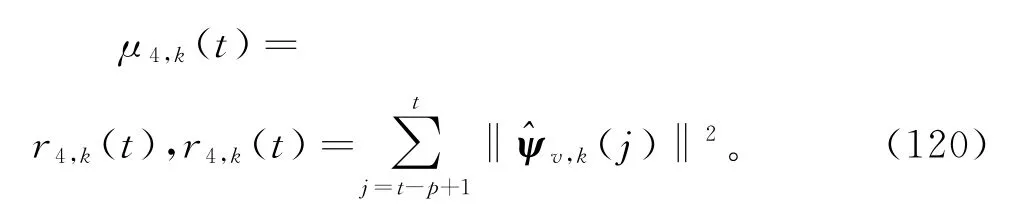
递阶多新息广义增广梯度迭代算法又称移动数据窗递阶广义增广梯度迭代算法(MDW-HGEGI算法)。H MI-GEGI算法(98)~(112)和(117)~(120)计算参数估计的步骤如下。
1)初始化:令t=1,给定移动数据窗长度p(通常取p≫n),参数估计精度ε,最大迭代次数kmax。置参数估计初值,。
2)令k=1,置。用式(106)~(107)构造输出信息向量φy(t-j)和输入信息向量φu(t-j),用式(108)~(109)构造噪声向量j)和。
3)采集观测数据u(t)和y(t)。用式(106)构造输出信息向量φy(t),用式(107)构造输入信息向量φu(t),根据式(117)和(118)计算步长μ1(t)和μ2(t)。
7)如果k<kmax,k就增加1,转到步骤(4);否则执行下一步。
5 递阶多新息广义增广最小二乘迭代方法
令k=1,2,3,…是迭代变量,和分别是参数向量a,b,c和d在时刻t的第k次迭代估计。令准则函数J9(a),J10(b),J11(c)和J12(d)在点a=和的梯度为零,得到
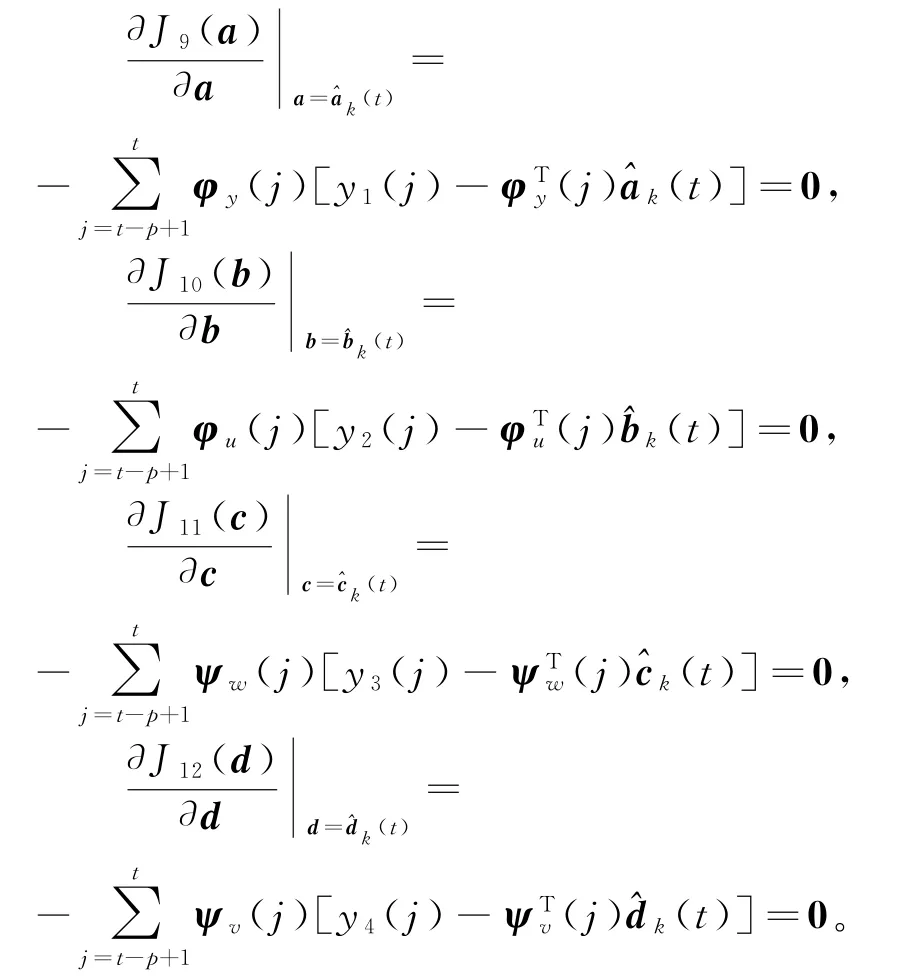
假设φy(t),φu(t),ψw(t)和ψv(t)是持续激励的,从以上4式可以求得

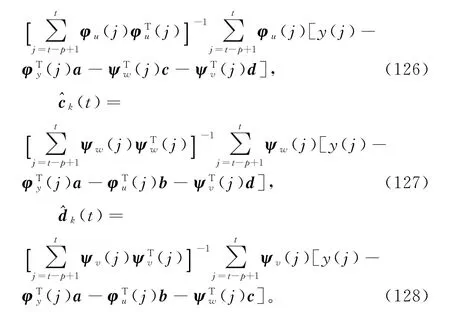
因为以上4式右边包含了未知参数向量b,c,d和a,以及未知噪声向量ψw(j)和ψv(j),所以无法计算出参数估计和。解决的办法是,未知噪声向量ψw(j)和ψv(j)用其估计和)代替,未知参数向量b,c,d和a用其前一次迭代估计和代替,代替后得到式(129)~(132),联立式(106)~(112),便得到估计参数向量a,b,c和d的递阶多新息广义增广最小二乘迭代算法(hierarchical multi-innovation generalized extended least squares-based iterative al gorit h m,HMI-GELSI算法):
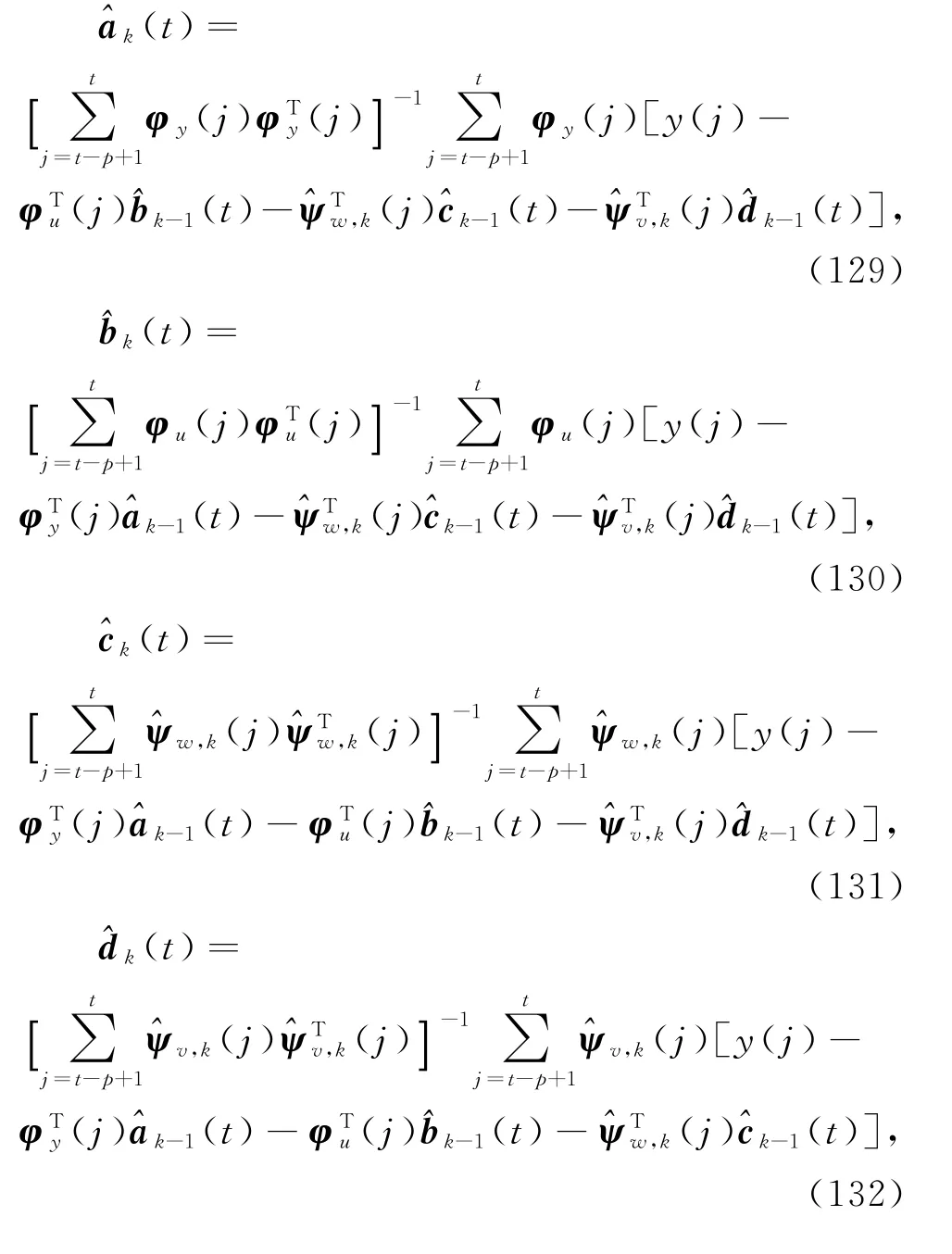
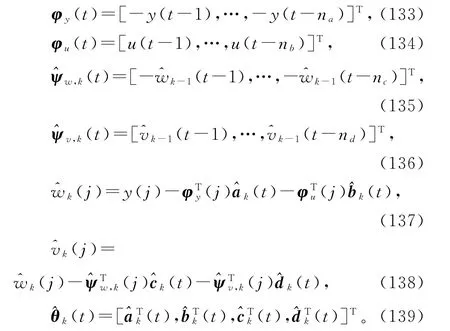
递阶多新息广义增广最小二乘迭代算法又称移动数据窗递阶广义增广最小二乘迭代算法(MDWHGELSI算法)。H MI-GELSI算法(129)~(139)计算参数估计和)步骤如下。
1)初始化:给定移动数据窗长度p(通常取p≫n),令t=l(l≥p),给定参数估计精度ε,最大迭代次数kmax。置参数估计初值。采集输入输出数据u(j)和y(j),j=1,2,…,l。置噪声初值=随机数,)=随机数,j=1,2,…,l。令nm=p+max[na,nb,nc,nd]。
2)令k=1,用式(133)~(134)构造输出信息向量φy(t-j)和输入信息向量φu(t-j),用式(135)~(136)构造噪声向量和,j=1,2,…,nm。
3)采集观测数据u(t)和y(t)。用式(133)构造输出信息向量φy(t),用式(134)构造输入信息向量φu(t)。
6)如果k<kmax,k就增加1,转到步骤4);否则执行下一步。
递阶多新息广义增广最小二乘迭代算法(129)~(139)可以等价表示为

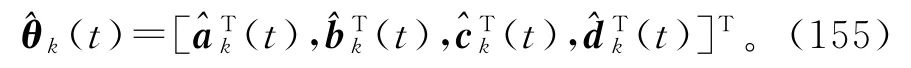
H MI-GELSI算法(140)~(155)计算参数估计和的步骤如下。
1)初始化:给定移动数据窗长度p(通常取p≫n),令t=l(l≥p),给定参数估计精度ε,最大迭代次数kmax。置参数估计初值,。采集输入输出数据u(j)和y(j),置^w0(j)=随机数,=随机数,j=1,2,…,l。令nm=p+max[na,nb,nc,nd]。
2)令k=1,用式(149)~(150)构造输出信息向量φy(t-j)和输入信息向量φu(t-j),用式(151)~(152)构造噪声向量和,2,…,nm,
3)采集观测数据u(t)和y(t)。用式(149)构造输出信息向量φy(t),用式(150)构造输入信息向量φu(t)。用式(144)构造堆积输出向量Y(p,t),用式(145)和(146)构造堆积输出信息矩阵Φy(p,t)和堆积输入信息矩阵Φu(p,t)。
7)如果k<kmax,k就增加1,转到步骤(4);否则执行下一步。
6 结 语
针对方程误差自回归滑动平均(EEARMA)系统,研究和提出了递阶(多新息)广义增广梯度迭代辨识算法、递阶(多新息)广义增广最小二乘迭代辨识算法。尽管这些递阶迭代辨识方法是针对有色噪声干扰下的标量方程误差随机系统提出的,但是其思想可以推广到有色噪声干扰下的线性和非线性多变量输出误差随机系统中[33-35]。

