墙体砌筑顺序对底商多层房屋抗震性能影响试验研究
齐芳月,郭迅,董策,王超
(防灾科技学院中国地震局建筑物破坏机理与防御重点实验室,河北三河 065201)
0 引言
在我国南方中小城镇,底商多层房屋应用十分广泛。汶川地震震害调查结果显示,底商多层房屋倒塌可致伤亡比例高达84.9%[1]。此类结构的底层因商用功能多设计为大开间框架结构,横纵墙体的数量比上部各层砌体更少,且层高更高,导致底层刚度最小。此外,上部各层重力逐层累加到底层,地震剪力同样逐层累加到底层。底层刚度小,受力大,在地震中为整个结构的薄弱层[2]。底层横墙数量多且满砌,纵墙数量少并开洞,横向抗侧刚度大于纵向,在地震作用下沿纵向更容易破坏[3]。楼板带动底层沿纵向发生平动,在相同侧向位移下,层间地震剪力按各道纵向轴线的抗侧刚度分配,造成地震力在内纵墙上凝聚[4]。尽管底商多层房屋的底层框架遵循“强柱弱梁”屈服机制进行抗震设计,但在实际地震中却表现为“弱柱强梁”,原因是在工程设计中填充墙并未被考虑在结构构件范围之内[5]。研究表明,上下墙体会约束梁,使之无法产生自由变形[6]。填充墙约束框架柱,产生的刚度效应和约束效应会造成短柱破坏,不利于结构抗震[7]。因此,填充墙的存在导致“强柱弱梁”难以实现,对底商多层房屋抗震性能的影响不可忽视。
现有研究大多关注填充墙的开洞率、开洞形式、砌体材料等因素对框架结构抗震性能的影响[8-13],但对填充墙砌筑顺序产生的影响研究较少。图1为实际震害中,填充墙的砌筑先后顺序导致的不同破坏模式:图1a为先砌墙后浇柱,窗间墙柱结合体呈现剪切破坏模式,出现“X”形交叉斜裂缝,墙体丧失承载能力;图1b为先浇柱后砌墙,填充墙出现斜裂缝呈现为剪切破坏模式,柱子和墙体剥离,在柱端出现塑性铰,呈现弯曲破坏模式,结构仍具有一定的承载和变形能力。可见填充墙砌筑先后顺序导致结构出现了不同的破坏模式,有必要对这种差异产生的原因进行更深入的研究。本文设计了3个1/4比例缩尺试验模型,分别为无填充墙RC框架模型(下文简称为OF)、开窗洞先砌墙RC框架模型(BF)、开窗洞后砌墙RC框架模型(AF),进行拟静力低周往复加载试验,对3个模型的破坏模式、滞回曲线、骨架曲线、刚度退化曲线进行对比分析,研究填充墙砌筑先后顺序对底商多层房屋抗震性能的影响。

图1 实际震害中墙体砌筑顺序导致的不同破坏模式Fig.1 Photos of different failure modes caused by the sequence of wall masonry in actual seismic damage
1 试验模型设计
1.1 模型尺寸
基于底商多层房屋底层纵向轴线构造特点设计了OF、BF、AF三种框架模型,均为单层两榀两跨缩尺框架。在AF、BF模型的边柱外侧窗下墙边设置与墙等高的钢筋混凝土柱,横截面尺寸为100mm×50mm,模拟结构底层中间跨纵墙受到两边跨墙体的约束。根据《混凝土结构设计规范》[14]和《建筑抗震设计规范》[5]要求,将模型均设计成“强柱弱梁”型。
各模型设计图和实物图见图2。OF为无墙RC框架,六根框架柱尺寸均为100mm×100mm×1000mm,分别命名为A1、A2、A3、B1、B2、B3。采用立模浇筑的施工方式以实现实际工程的施工效果。BF为先砌墙开窗洞RC框架,施工顺序为先砌筑开窗洞墙体并预留马牙槎,然后浇筑框架柱,同时设置拉结筋以加强墙和柱的连接。填充墙厚度为48mm,窗洞尺寸为480mm×600mm。AF为后砌墙开窗洞RC框架,施工顺序为先浇筑框架柱后砌筑开窗洞填充墙,同样设置拉结筋,墙上开洞与BF相同。3个模型框架柱材料、尺寸、命名均相同,柱上均设置加载梁,梁尺寸为2500mm×100mm×200mm,梁和柱同时浇筑。为防止框架柱与底板在拟静力加载过程中出现“提离”现象,特在柱底设置了柱墩加强对柱下端的约束,柱墩尺寸为200mm×200mm×120mm。框架柱底部与钢筋混凝土底板通过钻孔打眼植筋的方式连接,框架梁与钢筋混凝土盖板通过水泥与砂比例为1∶2的干硬砂浆相连,在盖板上放置铅块进行配重,施加竖向恒定荷载,荷载的取值根据设计轴压比确定。

图2 不同模型设计图及实物图Fig.2 Design drawings of three models and their corresponding physical photos
在满足《建筑抗震设计规范》[5]对框架结构轴压比规定的同时,参考汶川地震中倒塌的漩口中学教学楼底层柱的轴压比[6],将3组模型框架柱设计轴压比取值为0.31,由于每组试验混凝土实测强度不同,实际轴压比有所变化。单根柱子轴向压力按以下公式计算:

式中,N为柱子轴向压力,即每根柱分担的配重;fc为C20混凝土轴心抗压强度设计值,根据《混凝土结构设计规范》[14]取C20混凝土fc=9.6MPa;A为柱横截面面积;μ为设计轴压比。模型配重为六根柱子轴向压力之和,最终根据设计轴压比计算得到配重质量为18.22t。在试验时对模型配重进行了调整,最终OF、AF模型实际配重为15.85t、BF模型实际配重18.94t。框架柱设计剪跨比计算公式为:

式中,M为弯矩设计值;V取与M对应的剪力设计值;h为柱横截面高度。根据框架柱反弯点在柱中位置,可按下式计算设计剪跨比:
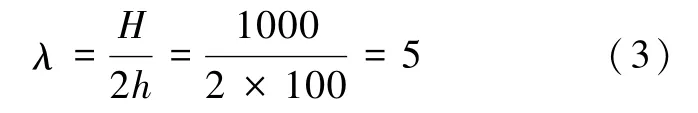
式中,H为柱净高;框架柱设计剪跨比为5。
1.2 梁、柱配筋
框架柱和加载梁的配筋图如图3所示。单根框架柱纵向受力筋采用4根8mm×8mm的矩形截面软钢,处理成麻花状,表面砸出凹痕增强与混凝土的黏结。单根梁采用6根φ6冷拉HRB335级带肋钢筋,梁柱箍筋均采用φ2HPB300镀锌铁丝,按50mm 等间距布箍,在梁柱节点处箍筋加密,25mm等间距布箍。框架柱保护层厚度设为5mm,配筋率2.6%,配箍率0.16%,加载梁保护层厚度设为10mm。
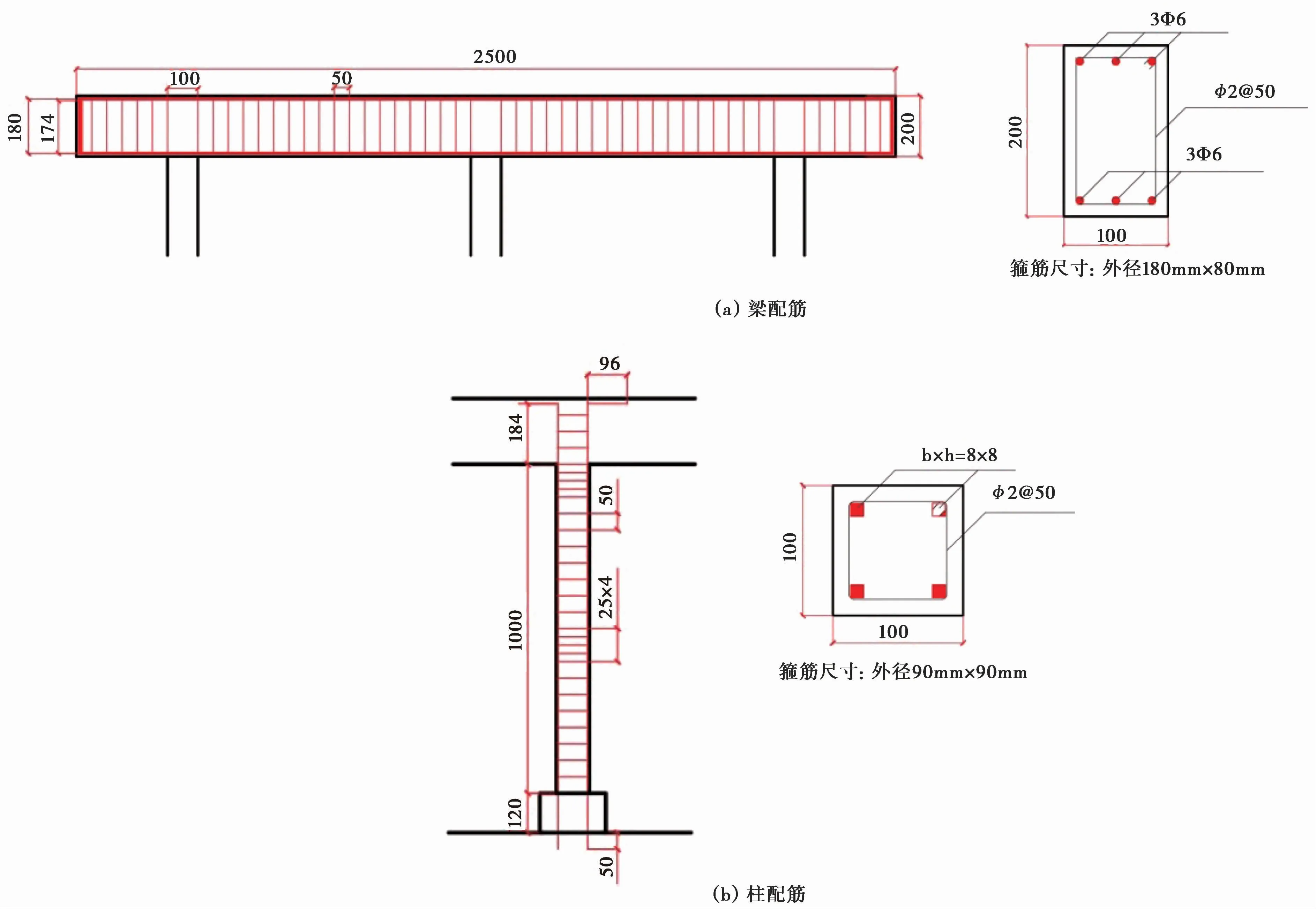
图3 梁、柱配筋图Fig.3 Reinforcement diagram of beam and column
1.3 模型材料
模型梁和柱所用C20混凝土均在实验室配制,配合比为1∶2.6∶4.0(水泥∶砂子∶石子)。填充墙由尺寸为98mm×48mm×48mm的预制混凝土空心砌块砌筑而成,砌块中空部分由1∶5的水泥砂浆进行填充,如图4所示。利用YAM200电液伺服压力机进行混凝土试块抗压实验得到C20混凝土相关参数。模型梁和柱所用钢筋如图5所示,矩形截面麻花状软钢利用MTS Model E45实验机进行拉伸实验获得其参数。各材料参数见表1。

图4 墙体砌块图Fig.4 Photo of wall blocks

表1 模型材料参数Tab.1 Model mater ial parameters

图5 模型梁和柱所用钢筋Fig.5 Photo of steel bars for beams and columns in the model
2 试验方案设计
2.1 加载方案
试验加载装置如图6所示。在模型梁上放置加载盖板,盖板上均匀堆叠铅块进行竖向配重(含盖板重量),施加给模型恒定不变的竖向荷载。水平荷载由MTS作动器施加在梁端,在MTS拟动力加载系统中输入位移幅值和频率,在水平方向上给模型顶部施加往复荷载。首次加载工况位移幅值为0.2mm,后续工况位移幅值成倍增长,每个工况均进行3个循环,加载制度如图7所示。当实验模型的承载力降到最大承载能力的85%以下或者模型发生严重损坏不足以进行下一工况时停止实验。

图6 试验加载装置Fig.6 Test loading device
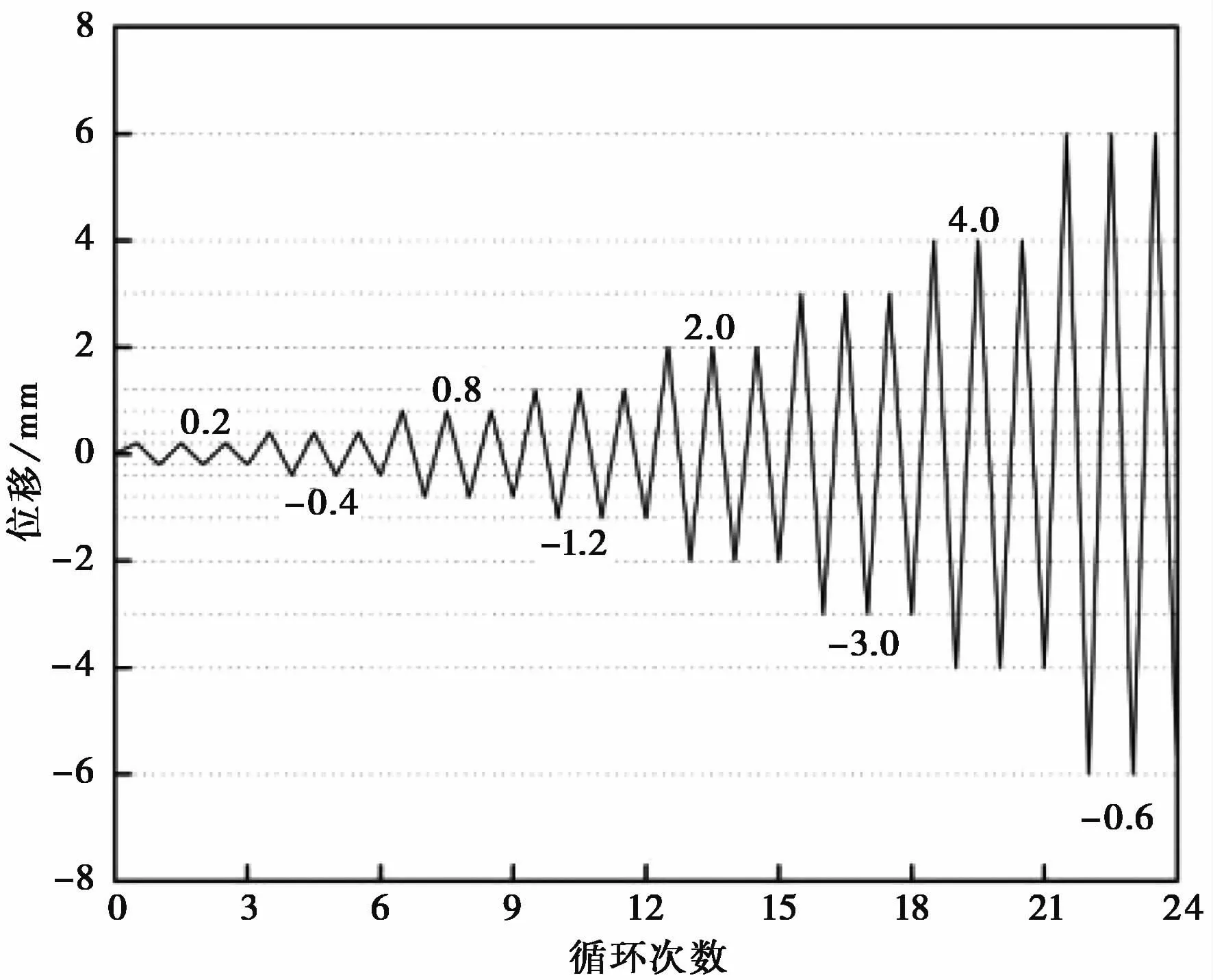
图7 实验循环加载方案Fig.7 The loading scheme of experimental cyclic
2.2 数据测量
外设DT-10位移计及LK-G500激光位移计测量每个实验工况下模型顶端实际侧向位移,位移计布置如图8所示。在模型的框架柱身布置了混凝土专用应变片(长度:6mm;电阻值:120.3±0.1Ω;灵敏系数:2.20±1%)测量关键受力区域的应变值。OF模型应变片贴设在柱顶、柱底及柱中,AF、BF模型应变片贴设在窗间柱柱顶、柱中以及柱底,柱顶和柱底分别左右对称贴设4片应变片,柱中前后对称斜45°贴设两片应变片,应变片的贴设情况如图9所示。所有荷载、位移和应变信号通过MTS-GT控制器和DH380东华应变采集仪自动采集。

图8 位移测量仪器布置Fig.8 Arrangement of displacement measur ing instruments

图9 应变片布置Fig.9 Layout of strain gauges
3 试验结果对比分析
3.1 破坏模式对比
3.1.1 OF模型
实际加载位移幅值为5.68mm之前,模型柱身未出现肉眼可见裂缝。实时显示的力-位移关系曲线成线性,卸载后变形基本回到零点,残余变形很小,可以忽略不计,模型基本处于弹性阶段。实际加载位移幅值为7.61mm时,在柱两端节点处混凝土开始出现细微裂缝。实际加载位移幅值工况为15.48mm时,柱节点混凝土裂缝沿横向发展至环绕柱身一周,同时沿柱身纵向钢筋位置处发展出竖向裂缝。加载位移幅值为31.59mm时,柱节点混凝土发展至压溃剥落,柱身纵筋处竖向裂缝进一步发展。荷载降到极限荷载的85.8%,OF模型加载试验结束。试件最终破坏形态见图10。

图10 OF模型最终破坏状态Fig.10 Ultimate failure modes of OF
3.1.2 BF模型
实际加载位移幅值为1.46mm时,模型未产生肉眼可见裂缝,处于弹性阶段。实际加载位移幅值为2.19mm时,首先在窗间墙上端出现细小的水平向裂缝,砌筑砂浆轻微掉落细小颗粒,同时混凝土柱的表面出现肉眼可见细小裂缝。实际加载位移幅值为4.27mm工况时,窗间墙上端裂缝连通,与加载梁的连接处掉落大块砂浆,模型的窗下墙受剪切破坏出现了宽度较小的X形交叉斜裂缝,扩展至窗洞下方的两角处。实际加载位移幅值增大到9.58mm时,模型受开窗洞墙体约束部分的短柱中部及柱顶出现斜裂缝,窗间墙上出现多条斜裂缝,此时窗下墙的裂缝并无多大发展,承载能力未失效,对窗下柱依然有约束作用。实际加载位移幅值为13.91mm时,裂缝持续开展,开窗洞墙柱结合体上形成了贯通斜裂缝,如图11a所示。实际加载位移幅值增加到17.94mm时,加载一圈半至正向位移峰值时A2柱瞬间丧失承重能力,A1、A3紧随其后失效,模型向A组柱一侧垮塌,图11b为倒塌前一刻A2、B2柱的破坏情况。

图11 BF模型破坏形态Fig.11 Failur e modes of BF
3.1.3 AF模型
实际加载位移幅值为2.01mm时,B2和B3两根框架柱旁的窗间墙与窗下墙分界处开始出现斜裂缝,柱身无裂缝出现。实际加载位移幅值为7.15mm时,模型窗间墙和窗下墙上均出现斜裂缝,砖缝间有砂浆颗粒掉落。A2柱与A3柱上部梁柱节点处出现肉眼可见裂缝。实际加载位移幅值为18.81mm时,各柱柱中出现多条斜裂缝,沿纵筋位置发展出竖向裂缝。A2柱中斜裂缝横穿整个截面,柱上部梁柱节点处砌块被压碎。在加载位移达到峰值点时可看到混凝土柱已与窗间墙间分离。实际加载位移幅值为39.11mm时,在窗间墙的上下端砌块已严重破坏,不断掉落碎块,柱与窗间墙之间通缝已肉眼可见。整个模型发生了偏移,认为其已丧失承载能力,试验结束。模型最终破坏形式如图12所示。

图12 AF模型破坏形态Fig.12 Failure modes of AF
3.1.4 模型破坏对比总结
OF模型柱两端的混凝土和钢筋间的黏结作用失效,混凝土剥落,非弹性变形集中发展,出现塑性铰,整体呈现延性弯曲破坏模式。
BF模型整体表现为剪切脆性破坏模式,将模型分为窗间墙柱结合体CW1、窗下墙柱结合体CW2两部分。二者中CW2变形能力较差,在加载过程中率先出现了细斜裂缝,但由于墙体抗侧刚度更大,能承担更多剪力,在后续的加载中裂缝没有明显发展。CW1出现沿45°方向剪切斜裂缝,裂缝发展迅速,率先失效,导致结构最终倒塌破坏。
AF模型率先在墙体出现剪切斜裂缝,后续墙体与框架柱分离,丧失对混凝土柱的约束作用,柱子继续承载剪力,在大位移下A2柱柱中斜裂缝贯通,表现为“短柱破坏”,模型整体发生偏移。AF总体呈现为剪切破坏模式,但又表现出一定的延性变形能力。
3.2 滞回曲线对比
结构在低周往复荷载作用下的力-位移滞回曲线能综合体现其承载力变化、延性能力高低、刚度退化趋势及耗能性能等多项抗震性能指标。模型BF、AF、OF的力-位移滞回曲线如图13所示,将3个曲线图设置了相同的横、纵坐标区间,方便进行对比分析。
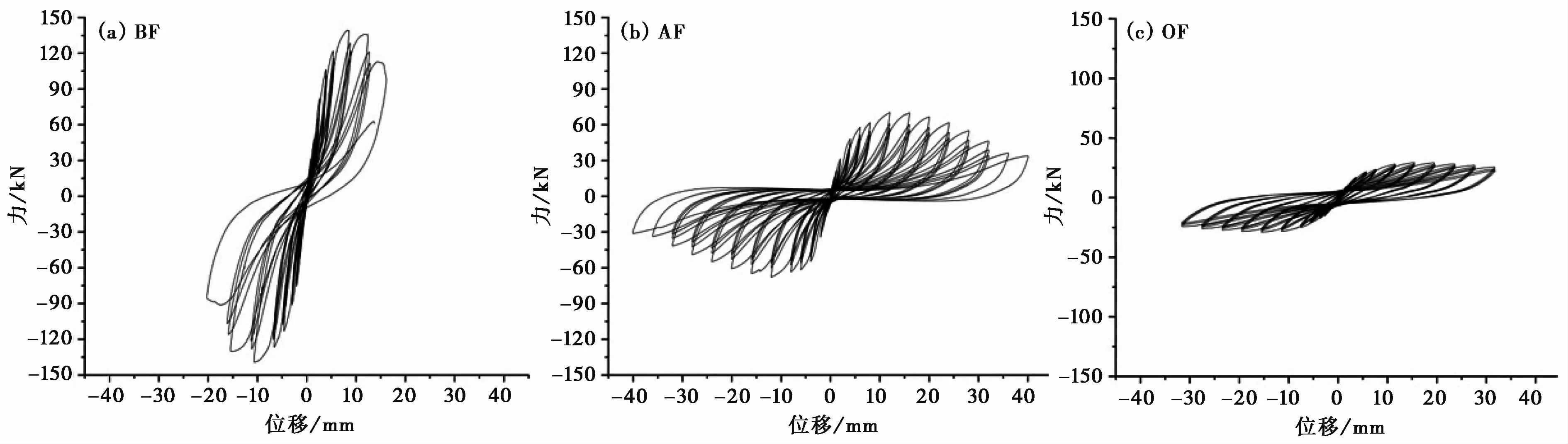
图13 滞回曲线Fig.13 For ce-displacement hysteresis curves of BF,AF and OF models
整体来看,在相同加载工况下,BF的荷载比其他两组模型增长更快,曲线坡度最“陡”,但滞回环数目最少,延性表现最差,最先破坏倒塌。实际加载位移幅值为9.58mm时,窗间墙短柱中部及柱顶出现多条剪切斜裂缝,后续工况中斜裂缝贯通并逐渐加宽,荷载同样快速下降,滞回环形状也迅速由梭形向“倒S形”过渡,表明模型出现了较大的剪切破坏,刚度严重退化。
模型OF的滞回曲线呈梭型,荷载增长缓慢,达到极限荷载后呈平缓下降趋势,试验结束时仍具有较大变形空间。OF在3组模型中承载能力最差,但延性较好,为延性破坏模式。
模型AF由于窗间墙前期率先破坏,与框架柱分离,窗间柱比BF模型发挥了更多延性能力,在达到极限荷载后,其滞回曲线下降段更加平缓。虽然AF整体表现为剪切破坏,但其滞回曲线在三者中最为饱满,耗能能力最强。
3.3 骨架曲线对比
每个加载工况有三次循环,选取第一次循环时的力-位移滞回曲线峰值点,将各工况下的峰值点相连得到的一条包络线作为模型的骨架曲线。绘制三组模型正向加载时的骨架曲线,并使用ORIGIN软件对骨架曲线进行了拟合处理。在拟合时选用多项式拟合方式,调整多项式阶以尽量保证拟合曲线通过或接近骨架曲线数据点,从而准确反映出模型承载力随加载位移不断增大时的变化趋势。基于骨架曲线拟合结果可量化对比三组模型的变形能力及承载能力。
3.3.1 变形能力对比
在地震荷载作用下,若结构具有良好的变形能力,可耗散掉更多的地震能量,能避免发生脆性剪切破坏突然失效。变形能力是评估结构抗震性能的一项重要指标,使用位移延性系数μ进行定量评估,μ越大,变性能力越强,计算公式为

式中,Δu为极限位移;Δy为屈服位移。因混凝土结构没有明显的屈服点,根据Park法[15],将骨架曲线承载力上升阶段的75%最大承载力作为屈服荷载,对应的位移为屈服位移Δy;将骨架曲线下降阶段的85%最大承载力作为极限荷载,对应的位移为极限位移Δu。三组模型骨架曲线上的屈服荷载、屈服位移、极限荷载、极限位移的选取如图14所示,位移延性系数计算结果如表2所示。结果显示,μBF<μOF<μAF,后砌墙框架结构变形能力最好。

表2 位移延性系数计算Tab.2 Calculation results of displacement ductility factor
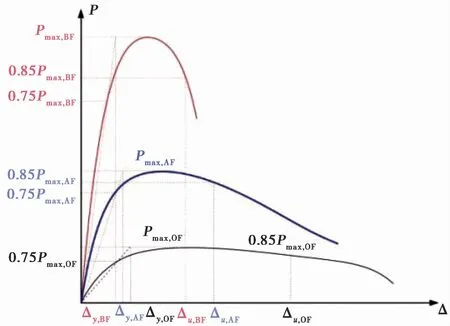
图14 位移延性系数计算参数选取Fig.14 Selection of calculation parameters of displacement ductility factor
3.3.2 承载能力对比
BF模型的最大承载力为139.28kN,对应的位移为9.58mm。在图15所示骨架曲线对比图上读取此位移下AF承载力为58.03kN,为其最大承载力 67.92kN 的 85%;OF 承载力为26.52kN,为其最大承载力29.24kN的91%。BF模型承载力最大,但其变形能力最小,AF模型尽管承载力小于BF模型,但其变形能力甚至超过了OF模型,因其既有一定的承载力又有一定的延性变形能力,三者中AF抗震性能更好。

图15 骨架曲线Fig 15 Compar ison of skeleton curves of the three models
3.4 刚度退化曲线对比
在加载位移幅值不断增大过程中,模型刚度逐渐减小,为对比三组模型的刚度退化情况,采用割线刚度法求取各工况结束后的模型刚度。割线刚度计算方法为:每级往复荷载最大值绝对值之和与其对应的框架顶部最大位移绝对值之和的比值[7]。根据计算结果绘制三组模型的刚度退化曲线如图16所示。
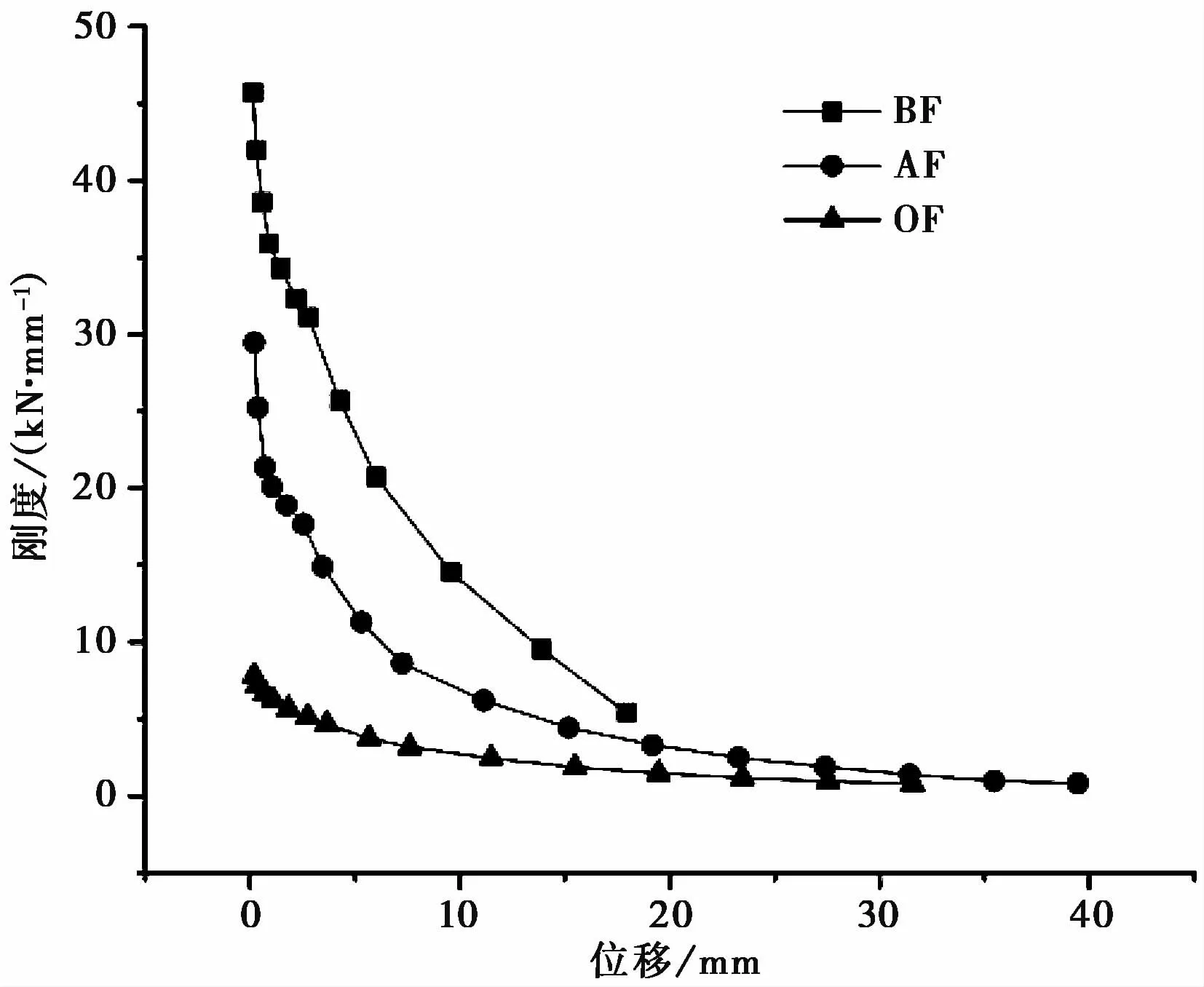
图16 刚度退化曲线Fig.16 The stiffness degradation curves of three models
各模型初始刚度最大的是BF模型,为45.70kN/mm,其次是AF模型,为29.47kN/mm,OF模型最小,为7.81kN/mm,三者初始刚度比值为5.85∶3.80∶1.00。OF模型刚度整体呈缓慢下降趋势,AF、BF刚度退化曲线在前期的走势基本相同,退化速度较快,后期AF模型失去承载能力后,BF模型刚度下降趋于平缓,且均大于同位移下模型OF的刚度。
刚度退化曲线对比结果表明,填充墙的存在会使模型初始刚度较大,但在遭受荷载作用后,有墙模型刚度下降更快,BF模型刚度退化曲线近似直线,AF在前期经历相同的下降趋势,但在填充墙失效后的刚度退化曲线出现和OF模型相同的缓慢下降趋势,证明后砌墙能使框架在具有比无墙框架更高承载能力同时还可使柱子发挥出延性变形能力。
4 结论
本文通过模型拟静力加载试验研究填充墙砌筑顺序对底商多层房屋抗震性能的影响,研究结果可为结构抗震设计及施工提供参考。主要有结论如下:
(1)模型BF、AF整体均表现为剪切脆性破坏。BF因窗间墙柱结合体出现贯通斜裂缝最终发生了倒塌,AF在加载过程中窗间墙率先发生剪切破坏并与框架柱分离,丧失了对混凝土柱的约束作用,试验加载后期由框架柱承担剪力,最后模型因一根框架柱出现了“短柱”破坏发生了偏移。
(2)模型AF耗能能力优于模型BF和OF,变形能力在三者中最好。模型BF尽管最大承载力较高,但变形能力最差。
(3)填充墙的存在会使结构初始刚度比无墙框架高出多倍,在荷载作用下刚度下降更快。AF、BF刚度退化曲线在前期的走势基本相同,退化速度较快,后期AF模型失去承载能力后,BF模型刚度下降趋于平缓,且在同位移下均大于模型OF的刚度。后砌墙能使框架在具有比无墙框架更高承载能力同时还可使柱子发挥出延性变形能力,对结构抗震最有利。

