典型单建式人防工程地震反应分析

沈冠豪，蔡晓光，黄鑫，，李思汉，徐洪路

（1.防灾科技学院地质工程学院，河北三河 065201；2.中国地震局建筑物破坏机理与防御重点实验室，河北三河 065201；3.河北省地震灾害防御与风险评价重点实验室，河北三河 065201；4.中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨 150080）

0 引言

近年来，世界范围内已有多次地震造成了地下结构发生损坏，尤其是1995年日本阪神大地震导致神户大开地铁车站发生了严重破坏，为此广大专家学者针对各类地下结构进行了深入研究，促进了地下结构抗震研究的发展。

李季等［1］通过软件建立某人防工程三维模型，计算结构在不同地震动作用下的地震响应，根据计算结果及相关规范建立了一种地下结构抗震评价方法。閤东东等［2］采用ANSYS和ABAQUS软件对某明挖地铁车站开展了动力时程分析，分析表明：地下结构中柱仍具有较大的富余量，地铁结构并未出现倒塌破坏。庄海洋等［3］以南京地铁为例，运用ABAQUS软件建模，研究了不同场地类别下地铁车站的地震反应，研究发现：当场地类别较差时，地震动峰值对结构层间位移角幅值影响较大。高照宇等［4］采用ANSYS软件建立地下商业街结构的三维有限元模型，研究不同埋深、不同地震动参数等因素对结构响应的影响，研究表明：在不同地震动作用下，地下结构的地震反应差异明显，其最大受力部位为结构的纵向跨中。冯进技等［5］通过振动台模型试验对某人防工程结构进行了动力响应研究，结果发现：地下人防工程的加速度响应普遍小于相同埋深下土体，结构中柱、构件连接处均为应力集中的易损部位。Zhuang等［6］研究了场地分类、地震动特性与输入地震动强度等条件对某大型地下地铁车站抗震性能的影响，并根据结构的层间位移角和地震损伤定义了5个抗震性能等级。张悦豪等［7］根据土－结动力相互作用，采用ANSYS有限元软件建立含三层地下室的框架结构开展三维整体地震反应分析，分析结果显示：地下室结构的顶底板处中柱受力较大。李宁等［8］采用FLAC 3D有限差分软件对某典型两层三跨人防工程板柱结构进行地震响应分析，研究发现：在9度抗震设防地震作用下，人防工程板柱结构的中柱为受力集中部位，抗拉、抗压强度均不满足规范要求。

目前国内外有关地下结构抗震的研究多集中在地铁车站，由于人防工程的敏感性，专门针对地下人防工程的抗震研究较少，当前仅有少数军事院校学者针对人防工程开展了相关结构抗震试验和数值模拟等研究工作。随着城市安全发展大局和韧性城市建设的需求，人防工程正逐渐融入城市应急体系之中，因此，有必要对人防工程在不同地震动作用下的地震反应进行专门研究，揭示其地震反应影响规律。

综上所述，本文以北京市某典型单建式人防工程为研究对象，建立了土－结构相互作用三维动力有限元模型，研究人防工程结构在不同地震动作用下的加速度、位移及内力等参数，分析该人防工程结构的地震响应、受力特征和抗震性能等。研究结果将对人防工程的抗震设计、抗震评估及加固改造设计提供参考与借鉴。

1 工程概况

根据该地区地质勘察报告，场地土层划分为7层，自上至下土层信息具体参数见表1。该地区抗震设防烈度8度，设计基本地震加速度0.2g，设计地震动分组为第一组，建筑场地类别为Ⅲ类。

表1 场地土层分布与参数Tab.1 Soil layer distribution and parameters of the site

该工程为地下两层多跨人防结构，建筑设计使用年限为50年，结构安全等级为二级，按6级人防工程进行设计。主体结构宽42m，层高3.5m，上覆土层厚1.5m，结构底板厚1.1m，顶板厚0.2m，中板厚0.2m，侧墙厚0.3m，中柱截面尺寸为0.7m×0.6m，暗柱截面尺寸为0.7m×0.3m，梁截面尺寸为0.6m×0.4m。中柱、暗柱和底板均采用C50强度等级混凝土；梁、侧墙、中板和结构顶板均采用C40强度等级混凝土。其中结构柱剖面示意图如图1所示。

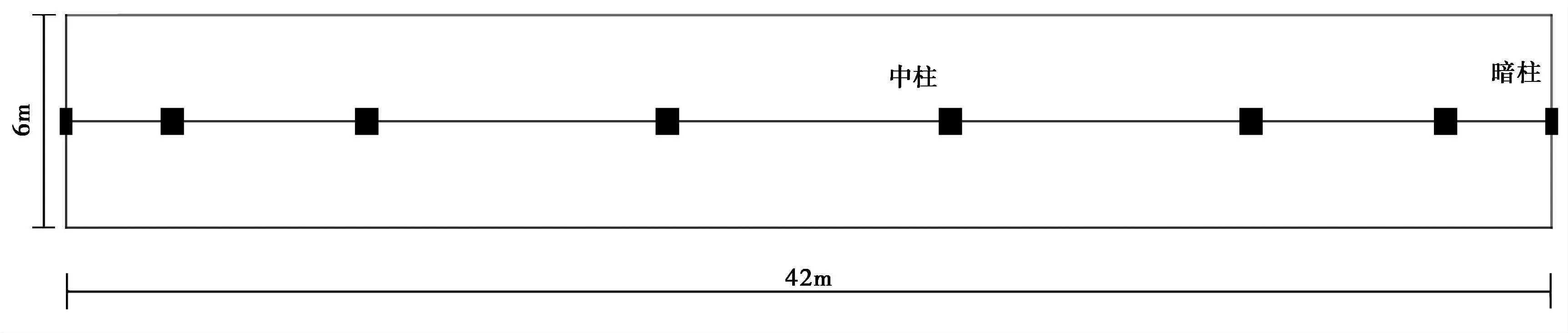
图1 地下人防工程结构柱剖面示意图Fig.1 Structur e column profile diagram of under ground civil air defense engineering

2 单建式人防工程数值模拟

2.1 模型建立

选取结构横断面宽度和高度的三倍范围分别作为整体模型的宽度和高度，以消除边界效应［8］。模型边界左右延伸126m，前后延伸6m，下部延伸至29.5m深度处，顶部埋深1.5m。该模型共203752个单元，219460个节点，模型四周选取自由场边界，底部采用固定边界，数值模型整体断面示意图如图2所示。

图2 模型整体断面示意图Fig.2 Schematic diagram of whole section of the model

2.2 材料参数

土体和地下人防结构采用三维实体单元模拟，在土体四周施加人工自由场边界单元以模拟无限远处土体。混凝土的本构模型采用线弹性模型，该模型是目前比较广泛采用的混凝土本构模型，结构材料参数如表2所示。土体的本构模型采用Mohr-Coulomb本构模型，该模型在GTS NX中应用比较广泛，土层材料参数如表1所示。

表2 结构材料参数表Fig.2 Material parameters of the structure

2.3 力学阻尼

在模型底部输入地震动时，需要考虑结构振动衰减，建模时必须考虑阻尼选取问题，本文选取瑞利阻尼（Rayleigh damping），如式（1）所示。

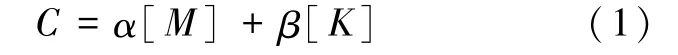
式中，［M］和［K］分别为质量和刚度矩阵。

α、β为常系数，通过式（2）和（3）可以确定：

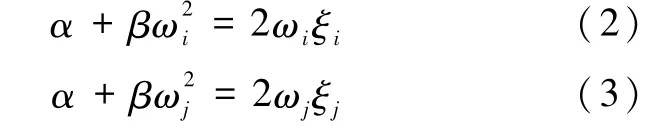
其中，ω、ξ分别为振型向量所对应的自振圆频率和阻尼比。通过振型分析结果可求得ωi、ωj，阻尼比通常取0.05。对结构进行特征值分析，得到一阶频率为0.389Hz，二阶频率为0.367Hz。

2.4 地震动选取

GBT51336-2018《地下结构抗震设计标准》［9］、GB50011-2010《建筑结构抗震设计规范》（2016版）［10］规定，采用时程分析法进行结构动力反应分析时，应采用不少于3组设计地震动时程，且实际强震记录数量不少于总数的2／3。

依据工程场地所在区域地震地质和地震活动性条件合成的北京人工波以及典型的El Centro波（1940年美国Imperial山谷地震El Centro台站地震记录）和Kobe波（1995年日本阪神地震神户海洋气象台地震记录）作为地震动时程输入，并对这3种不同地震动时程进行滤波和基线校正处理，得到合理的地震动时程。图3和图4分别为这3条地震动时程和傅里叶幅值谱，3种地震动时程的卓越频率分别为1.904Hz、0.586Hz和2.392Hz。总体来看，3种地震动中北京人工波的傅里叶谱频带宽度最大，El Centro波的频带宽度次之，而Kobe波的傅里叶谱频带宽度最小。

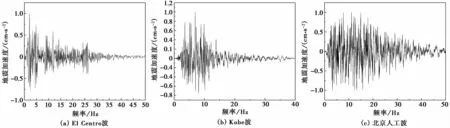
图3 归一化的El Centro波、Kobe波和北京人工波时程曲线Fig.3 Normalized time history curves of El Centro，Kobe and Beijing artificial waves

图4 输入地震动傅里叶幅值谱Fig.4 Fourier amplitude spectr um of the input gr ound motion

在模型计算时考虑该地区为8度抗震设防，根据GB50011-2010《建筑结构抗震设计规范》（2016版）［10］，将3种地震动时程进行归一化，然后调幅［11］为8度抗震设防所对应的多遇、基本和罕遇地震加速度峰值70cm／s2、200cm／s2和400cm／s2，共9组地震动时程，分别加载至模型底部。

3 计算结果及分析

3.1 加速度响应特性

3.1.1 加速度放大系数

本文采取结构不同高度处的均方根加速度值与结构底部均方根加速度值的比值作为加速度放大系数，均方根加速度计算公式如式（4）所示。

式中，aRMS为均方根加速度；Td为地震动持续时间；a（t）为地震动时程。通过图5罕遇地震动作用下地下人防工程沿结构不同高度处的均方根加速度放大系数图可知：地下人防工程结构的加速度放大系数随墙高的增大而增大；在El Centro波作用下，结构同一高度处的加速度放大效应最为明显，大于Kobe波和北京人工波作用下的加速度放大系数；在结构墙高4.5m以下部分，Kobe波作用下的加速度放大系数大于北京人工波作用下的加速度放大系数，而在结构墙高4.5m以上部分，北京人工波作用下的加速度放大系数大于Kobe波作用下的加速度放大系数。

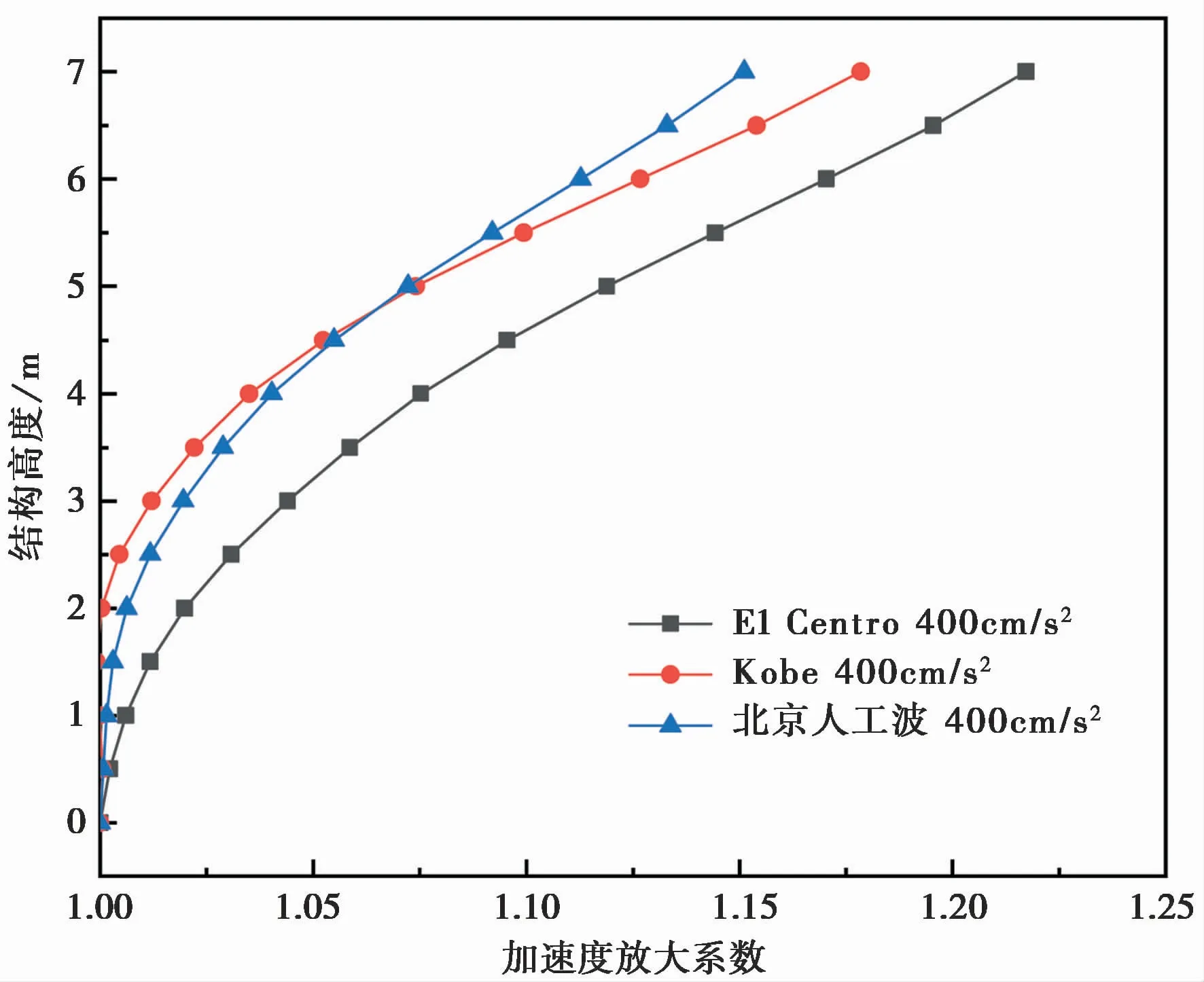
图5 结构不同高度处均方根加速度放大系数Fig.5 Root mean square acceleration amplification coefficient at different height of structure

3.1.2 加速度峰值

加速度峰值（Peaking Ground Acceleration，PGA）是评判结构受地震破坏程度的重要指标，同时也是结构抗震设计的参考依据。在该地下人防结构上监测楼板、中柱及暗柱等不同部位处的加速度，图6给出了结构侧墙中部不同高度处的加速度峰值，其不同典型位置处的加速度峰值如表3所示。

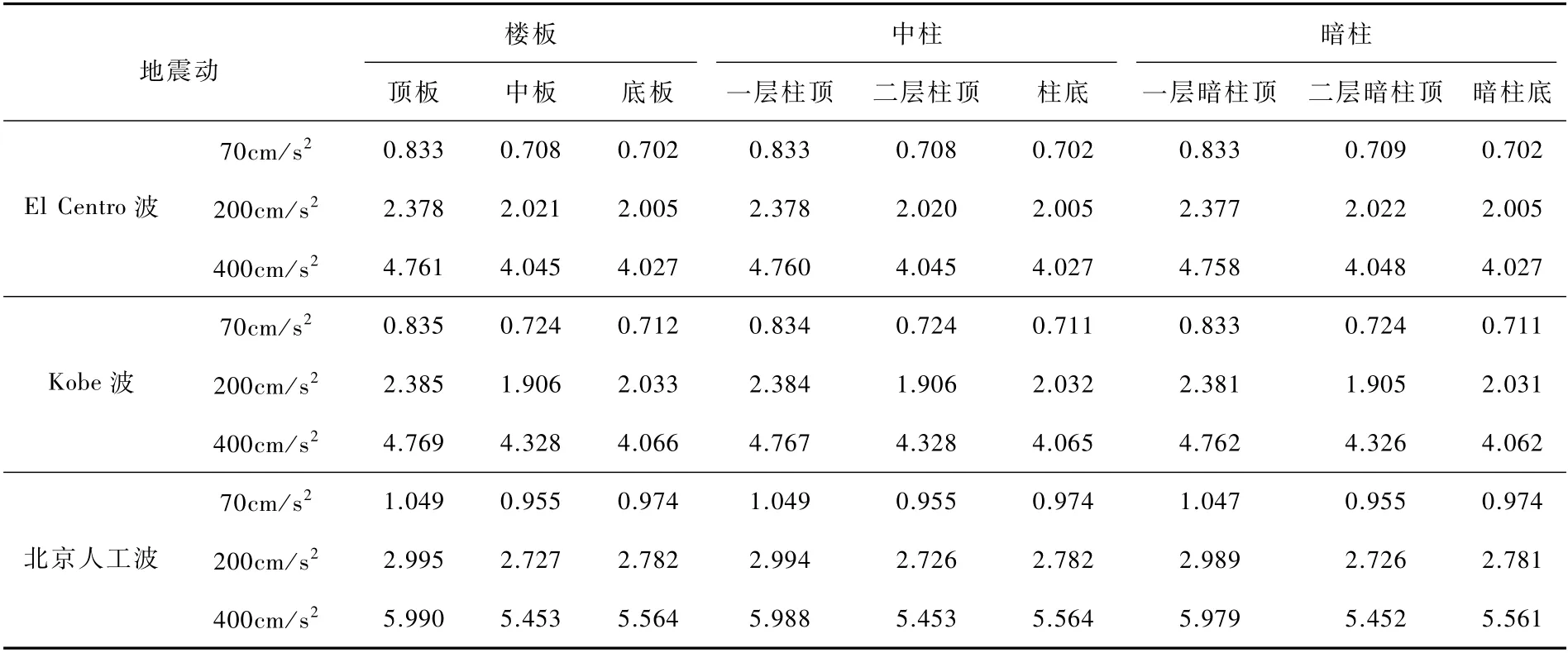
表3 不同地震作用下地下人防工程不同部位处加速度峰值（m／s2）Tab.3 Peak acceleration at different positions of underground civil air defense engineering under different ground motion （m／s2）

由图6可知，在多遇地震动作用下，结构不同高度处的加速度峰值基本保持一致，无明显变化；在基本和罕遇地震动作用下，结构底部高度处的加速度峰值基本保持一致，但在中上部高度处发生明显的转折，加速度峰值随结构高度增加而发生明显增大。

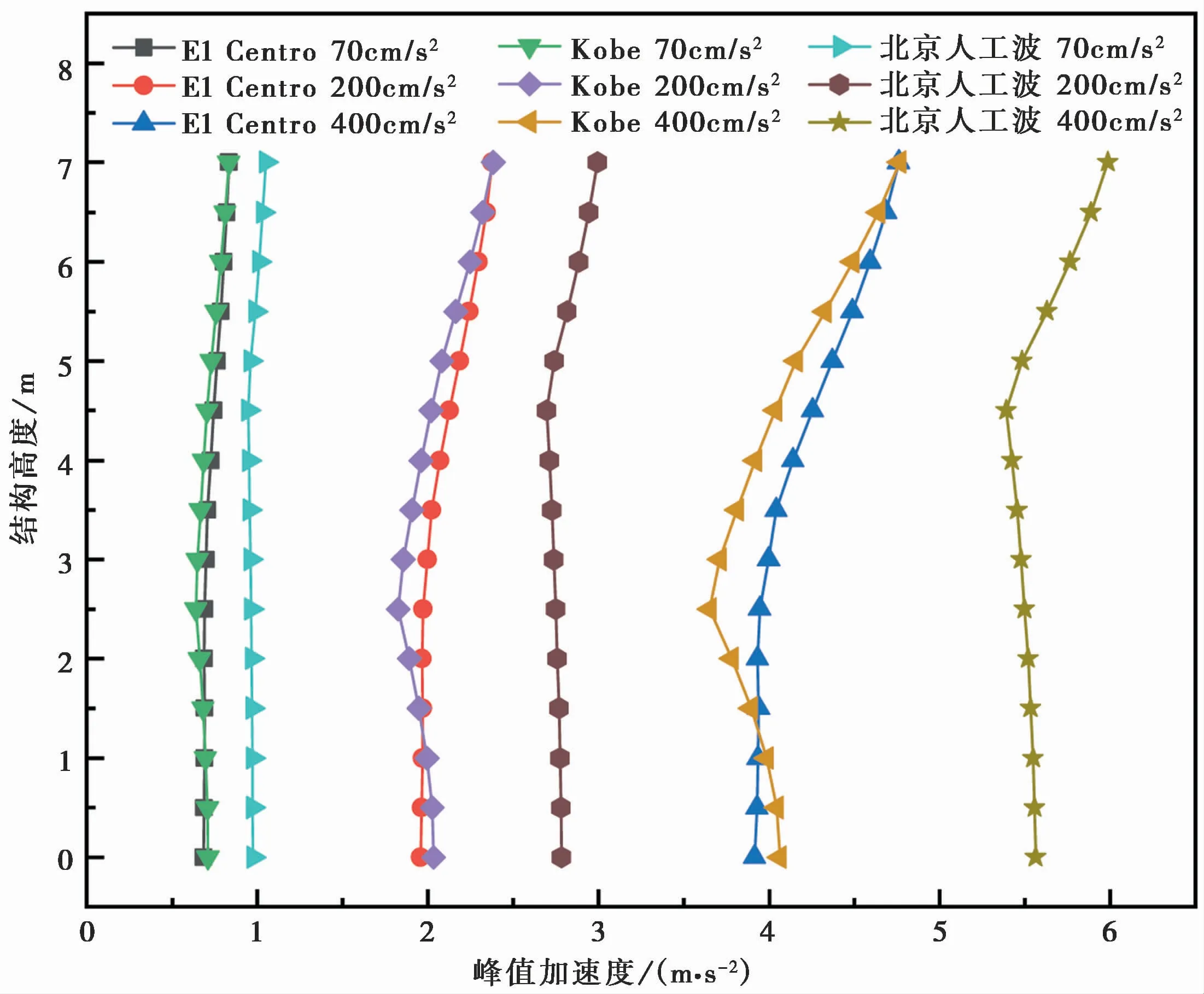
图6 加速度峰值沿墙高分布Fig.6 Distribution of peak acceleration along wall height

由表3可以看出，在结构底部输入同一地震动时，结构楼板、中柱及暗柱在同一高度处的加速度峰值基本一致，无较大变化；在同一地震动作用下，结构顶板的加速度峰值要大于中板及底板，地下一层柱顶处的加速度峰值大于地下二层柱顶及柱底加速度峰值，地下一层暗柱顶部的加速度峰值大于地下二层及暗柱底部的加速度峰值，这是由于地震动由下部土层传播到结构顶部，土层和结构对地震动具有一定的放大作用，其结果与李宁等［8］研究结果一致。结构在不同地震动输入下，同一部位处的加速度峰值也不相同，其中北京人工波作用下结构的加速度峰值要略大于El Centro波和Kobe波作用；在不同地震动幅值输入下，结构不同部位处的加速度峰值随输入地震动峰值的增大而增大，其中在北京人工波400cm／s2输入下，结构的加速度峰值达到最大，最大位置发生在地下人防工程一层顶板位置处。

3.1.3 频谱分析

地震动经过土体传播到地下人防工程结构，地震动的特性发生改变，本文给出了在El Centro波、Kobe波和北京人工波不同幅值（70cm／s2、200cm／s2和400cm／s2）输入时，地下人防工程结构中柱不同位置处（地下一层中柱顶部、地下二层中柱顶部和地下二层中柱底部）加速度时程的傅里叶幅值谱，如图7、图8和图9所示。

由图7、图8和图9可知，在不同幅值地震动时程的作用下，傅里叶幅值谱在0.389Hz附近均存在明显的峰值，说明结构在自振频率附近均存在放大作用；在同一地震动的不同幅值作用下，结构中柱不同部位处的傅里叶幅值谱的幅值随地震动强度的增大而增大；在同一地震动作用下，结构不同位置处的频谱特性不同，地下人防工程结构中柱从地下二层底部到地下一层顶部处的傅里叶幅值谱的幅值逐渐增大，符合地震波经土体和结构的放大效应。当输入的地震动卓越频率不同时，经过土－结构相互作用的传播，对中柱不同位置处的傅里叶幅值谱的变化影响较小，其结果与潘丹光等［12］的振动台试验研究结果一致。

图7 El Centr o波作用下结构中柱不同部位处傅里叶幅值谱Fig.7 Fourier amplitude spectr a at different positions of columns in structures under El Centro ground motion

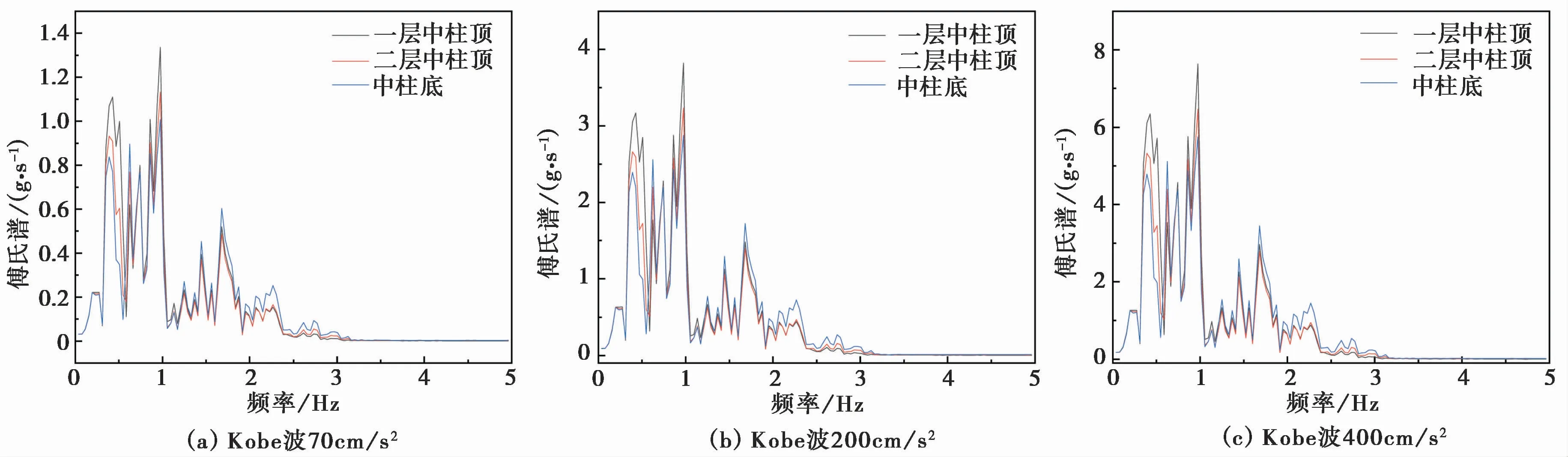
图8 Kobe波作用下结构中柱不同部位处傅里叶幅值谱Fig.8 Fourier amplitude spectrum at different positions of the column under Kobe ground motion

图9 北京人工波作用下结构中柱不同部位处傅里叶幅值谱Fig.9 Fourier amplitude spectra at different positions of column under Beijing artificial ground motion

3.2 位移响应特性

在土－结构相互作用下，地下土层发生的相对变形会直接影响到地下人防工程结构，从而导致结构发生变形，考虑地下人防工程结构发生的相对位移对结构的地震反应分析尤其重要，因此将地下人防工程结构不同高度处的相对水平位移幅值和结构底部相对水平位移幅值的差值定义为人防工程结构的相对水平位移［13］。不同地震动输入下地下人防工程结构侧墙暗柱部位处的相对水平位移沿高度的变化曲线如图10所示；地下人防结构相对水平位移的最大值如表4所示，层间位移角是反映结构层间刚度的一个重要指标，表5给出了地下人防工程结构在不同地震动作用下的各层层间位移角。

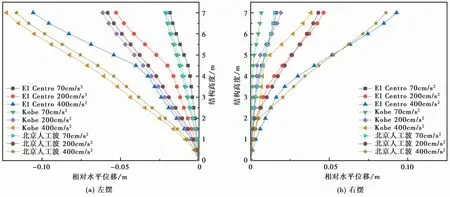
图10 不同地震动输入时地下人防工程结构的相对水平位移Fig.10 Relative horizontal displacement of underground civil air defense engineering structure under different ground motion

表4 不同地震动输入时地下人防工程结构的相对水平位移最大值（m）Tab.4 The maximum relative horizontal displacement of underground civil air defense engineer ing structure under differ ent ground motion （m）

表5 不同地震作用下地下人防结构各层层间位移角Tab.5 Displacement angle between layers of underground civil air defense structure under different ground motion

由图10可以发现：从宏观上看，左摆和右摆曲线相似，但是从相对位移的幅值上对比发现，右摆相对位移幅值要小于左摆相对位移，这是因为在地震动作用下，地下人防工程结构产生了单方向累积的残余位移，和陈磊等［13］的研究结果类似。在El Centro波、Kobe波和北京人工波都在幅值400cm／s2输入下，结构发生的相对位移最大，其中地下人防工程结构左摆的最大相对位移为0.123m，发生在Kobe波400cm／s2作用下的暗柱顶部，右摆最大相对位移为0.106m，发生在El Centro波400cm／s2作用下的暗柱顶部。

在Kobe波400cm／s2输入下，左摆产生的相对位移和El Centro波400cm／s2、北京人工波400cm／s2作用下左摆的相对位移大体一致，但右摆产生的相对位移却小于El Centro波200cm／s2和北京人工波200cm／s2作用时产生的相对位移。分析输入的地震动时程曲线图3可知，Kobe波峰值仅出现一次且持续时间较短，此外Kobe波加速度时程在方向上也具有一定的差异性，Kobe波正向的幅值大于负向幅值，在对其进行调幅时，随着幅值的增大其差异性也更加明显；从输入地震动时程的傅里叶幅值谱上也可以明显看出北京人工波的傅里叶谱频带宽度最宽，Kobe波的傅里叶谱频带宽度最窄。分析发现：造成Kobe波400cm／s2作用下右摆相对位移较小的原因，一方面是由Kobe波自身的频谱特性所造成的；另一方面由于Kobe波加速度时程在方向上的差异性与结构产生单向累积残余位移的叠加造成左摆的相对位移大于右摆。

由表5可知，在北京人工波400cm／s2输入时，地下一层的最大层间位移角达到1／369，满足GB50011-2010《建筑抗震设计规范》（2016版）［10］要求罕遇地震作用下弹塑性层间位移角规范限值1／50，满足结构变形要求，且仍有较大的强度储备。

3.3 内力响应特性

通过在地下人防工程结构底部输入不同幅值的3种地震动时程，获得了地下人防工程结构不同柱子处的内力响应，如表6所示。由于在3种地震动作用下结构的内力反应规律基本一致，以下仅列出了结构在El Centro波70cm／s2作用下不同部位处的内力时程曲线，如图11所示。

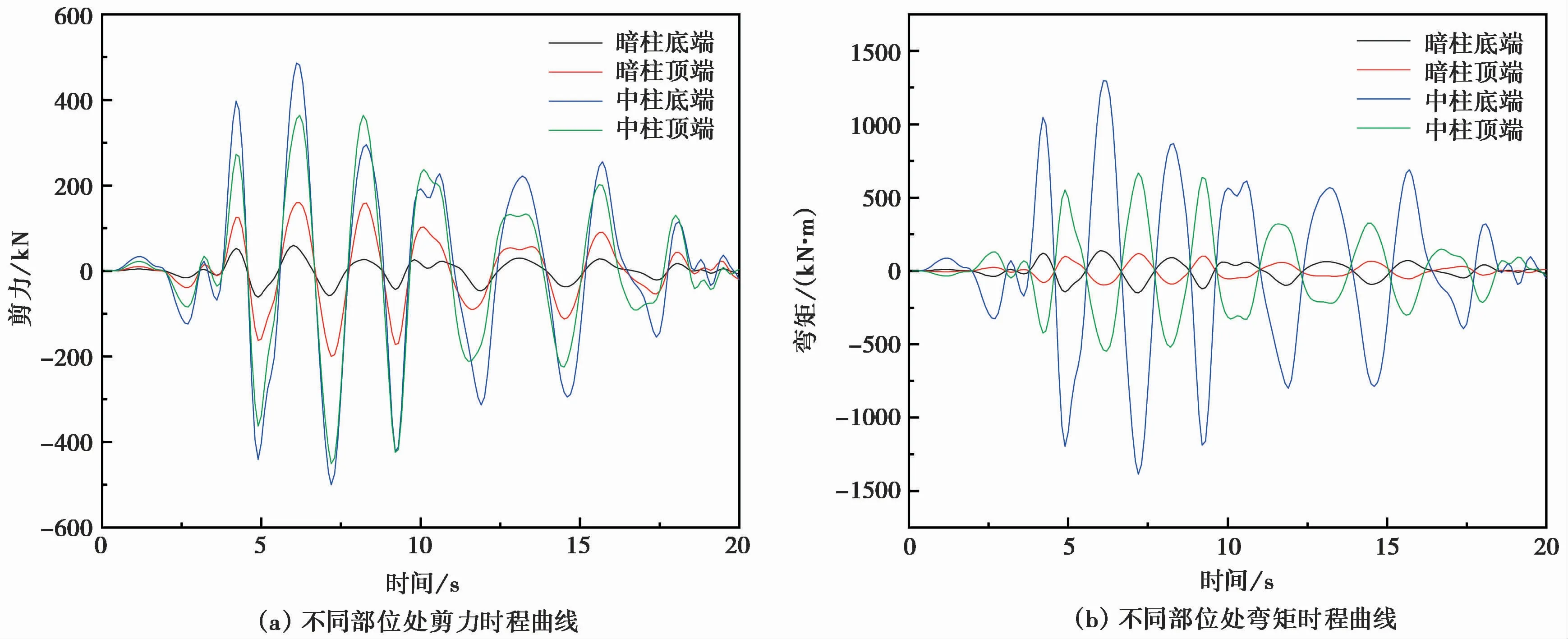
图11 El Centro波70cm／s2作用下地下人防结构内力时程曲线Fig.11 Time-history curve of internal force of underground civil air defense structure under El Centro wave 70cm／s2

由表6可知，在相同峰值的不同地震动时程作用下对地下结构不同柱子类型、不同柱子部位的影响也不同，这是由于地下人防工程结构暗柱受到侧墙以及周围土体的约束作用，地下人防工程暗柱的内力反应较小。其中在El Centro波作用下，中柱内力整体大于暗柱内力，其剪力最大为2573.927k N，其最大弯矩为3801.884k N·m，均出现在400cm／s2作用时地下人防结构中柱底端位置；在Kobe波和北京人工波作用下最大剪力和最大弯矩均出现在400cm／s2作用时，其最大剪力和弯矩出现的部位也与El Centro波作用下一致。

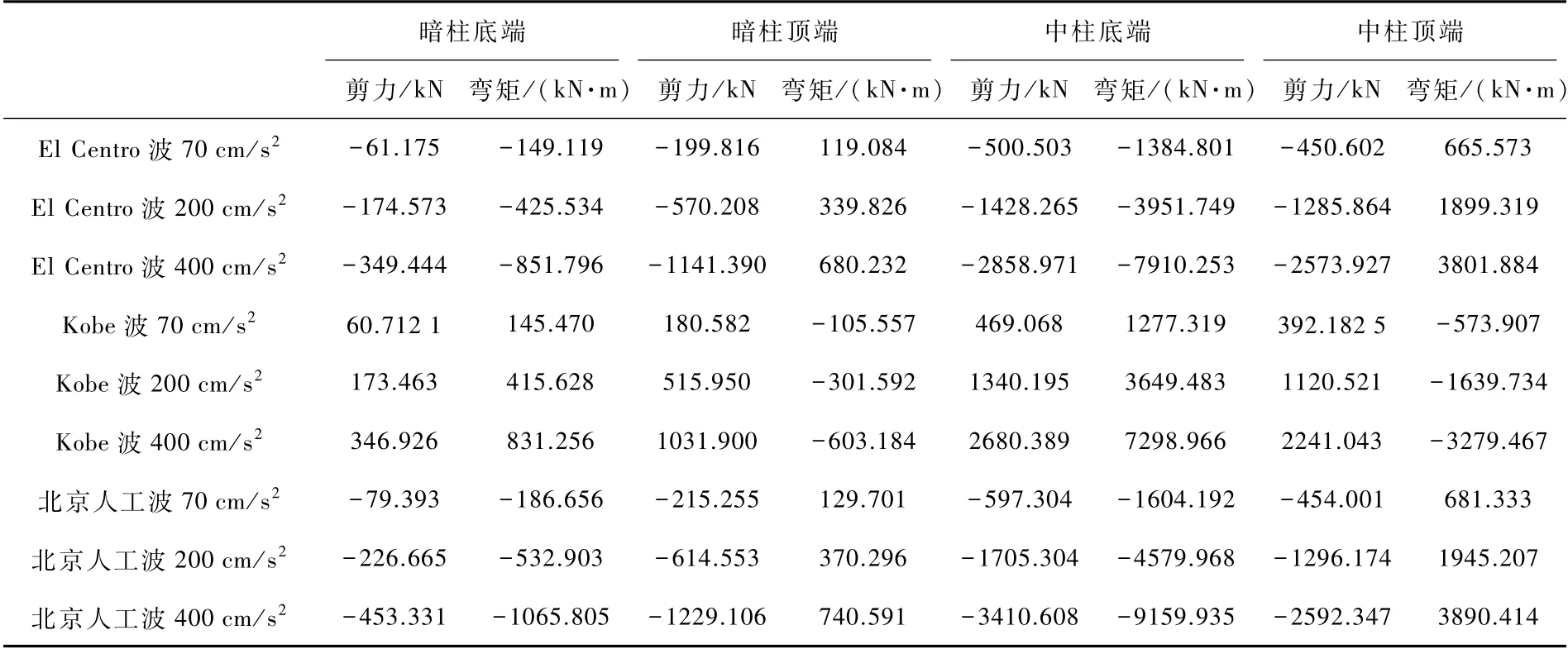
表6 地下人防工程结构柱子处内力响应幅值Tab.6 Response amplitude of internal force at the column of underground civil air defense engineering

由图11可知，在同一地震动作用下，地下人防工程结构中柱和暗柱的剪力时程曲线均与输入的加速度时程波形基本一致，且内力峰值也均出现在输入的地震动峰值位置附近。结构中柱底端剪力大于中柱顶端的剪力，结构暗柱底端剪力大于暗柱顶端剪力，且地下中柱的剪力和弯矩值均大于地下暗柱的剪力和弯矩值。

4 结论

本文对北京市某典型单建式人防工程进行了不同地震动作用下的数值模拟，研究了结构的加速度、位移以及内力等响应参数，得到以下结论：

（1）在输入相同加速度幅值的不同地震动时，该地下人防结构在北京人工波作用下地震反应最大，在El Centro波和Kobe波地震作用下结构反应接近，说明输入地震动的频谱特性不同对结构的影响不同，结构的地震反应与选取的地震动有紧密联系。

（2）在罕遇地震动作用下结构层间位移及最大层间位移角达到最大，但仍然在规范限制的范围内，说明该地下人防工程结构整体抗侧向变形能力良好。

（3）在不同幅值地震动作用下，地下人防工程中柱的内力反应最大，其剪力和弯矩均大于暗柱，且中柱最大剪力和弯矩均发生在中柱顶端位置处，中柱仍然是抗震的薄弱环节，容易发生变形和开裂等破坏，在抗震设计时需要重视。