兼顾能力与知识状态的Higher-Order CD-CAT选题方法
席崇钦,涂冬波,蔡 艳
(江西师范大学心理学院,江西 南昌 330022)
0 引言
计算机化自适应测试(computerized adaptive testing,CAT)是利用现代化信息技术实现的自适应测试形式,通过“量体裁衣”式的自适应技术,满足高效精准的测试需求.基于项目反应理论的IRT-CAT,可以高效精准地获取被试的终结性评价(常称为能力),用于评估被试整体表现.此外,反映被试微观认知结构或认知过程的形成性评价(常称为知识状态或属性掌握模式)也同样重要,这些信息不仅有助于教师更好地“因材施教”[1-2],而且有助于心理学家探索被试在解决问题时的认知过程[3]和精神病学家诊断患者的心理症状[4].基于认知诊断理论,研究者们开发出具有认知诊断功能的计算机自适应测验(CD-CAT),以快速精准地获取被试的形成性评价.另外,在心理与教育的实际应用中,终结性评价和形成性评价同等重要,即同时关注能力和知识状态,使得整体的评价与具体的干预或补救达到和谐统一(如美国“Race to the Top”(RTTT)推行的联邦赠款计划[5]).为了高效地获取这2个方面的信息,研究者们开发出了双目标CD-CAT(dual-objective CD-CAT)[1,6].
根据采用的模型不同,双目标CD-CAT可划分为使用单一模型和分离建模2种类型[1,7].基于分离建模的双目标CD-CAT采用双标定过程(dual-calibration process)标定题库的项目参数,即题库中的每个项目分别由项目反应模型(item response model,IRM)和认知诊断模型(cognitive diagnostic models,CDMs)标定,因此每个项目有2套不同的参数.然而,有研究者[1,8-9]认为应谨慎使用双标定过程标定项目参数,其原因是:IRM和CDMs的潜在结构完全不同,其中IRM的潜在结构是连续变量,而CDMs的潜在结构是离散变量.换言之,基于分离建模的双目标CD-CAT是一种存在缺陷的、折中的双目标CD-CAT[1,9].为此,C.L. Hsu等[1]建议双目标CD-CAT采用能同时描述能力和知识状态的单一模型(如高阶模型(higher-order cognitive diagnosis models,HO-CDMs))[10],并在此模型基础上提出了Higher-order CD-CAT.在Higher-order CD-CAT中,被试的能力由高阶能力表示,该能力主导被试的知识状态,而知识状态又直接影响项目反应.由于该CAT系统的项目参数只由HO-CDMs来标定,因此每个项目仅有1套参数.与分离建模相比,单一模型的题库建设成本更低,其原因是:前者的项目要同时拟合IRM和CDMs,条件比较苛刻,而后者的项目只需要拟合HO-CDMs.
然而,由于尚未开发出适用于Higher-order CD-CAT的选题方法,这将导致该CAT系统只能采用单目标选题方法(即只对知识状态自适应),这可能导致能力的估计精度不高.虽然已有对知识状态和能力同时自适应的双目标选题方法[2,6-7,9,11-14],但是这些方法均是建立在分离建模基础上的,无法应用于Higher-order CD-CAT中[1,7-8].其主要原因是:Higher-order CD-CAT只标定1套项目参数,而当前的双目标选题方法需要2套项目参数.在Higher-order CD-CAT中,若需同时精确估计被试的能力和知识状态,则其选题就应同时考虑这2个变量.基于这个思想,本文在后验加权库尔贝克-莱布勒信息量法(Posterior-Weighted Kullback-Leibler,PWKL)选题方法的框架下,结合HO-CDMs的原理,提出适用于Higher-order CD-CAT、兼顾能力和知识状态的新选题方法.
1 认知诊断模型
认知诊断是认知心理学与心理计量学相结合的产物,在CDMs中它融合了相关认知变量以实现对被试的诊断与分类[15].设向量Xi=(Xij),其中Xij为被试i在项目j上的作答,i=1,2,…,N,j=1,2,…,J.设被试i的知识状态为αi=(αik),其中k=1,2,…,K,当被试i掌握属性k时,αik=1,否则αik=0.项目与属性之间的关系用J×K的Q矩阵表示[16];在该矩阵中当第j行第k列的元素qjk=1时,项目j测量了属性k;当qjk=0时,项目j没有测量属性k.
拓广DINA模型(generalized DINA,G-DINA)为由de la Torre J[17]在DINA模型[18]基础上拓展的饱和模型,该模型同时考虑了属性的主效应和所有可能的交互效应.目前许多CDMs是G-DINA模型的简化版本,即通过约束特定条件,使得G-DINA可以转换为不同的简化CDMs.如当属性仅存在主效应而无交互效应时,G-DINA可简化为A-CDM模型[17].
为了同时描述被试能力θ和知识状态α,de la Torre J等[10]通过层次框架结构将θ和α连接起来,开发出了高阶模型(HO-CDMs).其中被试θ主导α(水平2),而α影响其在项目上的作答结果(水平1).若被试的θ水平越高则其掌握某个属性的概率越大,能力θ和属性αk的关系为
P(αk=1|θ)=exp(1.7λ1k(θ-λ0k))/(1+exp(1.7λ1k(θ-λ0k))),
(1)
其中λ0k为属性k的截距,λ1k为属性k的斜率参数,θ为服从标准正态分布的高阶能力.在属性间局部独立的假设下,当被试i的能力为θi时,其知识状态为αi的条件概率为
(2)
在HO-CDMs框架下,任何CDM都可以作为项目反应函数[10].当同时考虑属性的主效应和所有的交互效应时,水平1的项目反应函数应采用G-DINA模型,此时称之为HO-GDINA.
2 适用于Higher-order CD-CAT的新选题方法

(3)
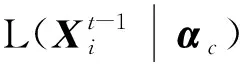
设P(Xij=x|αc,θr)为被试i在项目j上的作答概率,任意2个作答概率之间的差异可用KL信息[19]度量.在CD-CAT中,KL类的选题方法均是基于KL信息开发而得的,其中PWKL选题方法因其优越的选题性能和简洁的计算方式而被广泛使用.因此,本文基于PWKL的选题思想,结合高阶模型的特性,拟开发适用于Higher-order CD-CAT、同时兼顾α和θ的HO-PWKL选题方法,其计算方法为
HO-PWKL选题方法的目标函数为

3 模拟实验
为了检验HO-PWKL与传统选题方法在Higher-order CD-CAT中的选题性能,本文开展了2项Monte Carlo模拟实验.
3.1 实验条件
实验1和实验2均包括3个自变量:(i)测量属性个数(分别包含5个属性和8个属性);(ii)测验长度(短测验和长测验),由于测量的属性个数越多,需要的项目就越多,因此5个属性的短测验和长测验分别设为10题和20题,8个属性的短测验和长测验分别设为15题和30题;(iii)选题方法,本文采用的选题方法均为KL类的方法,包括KL、HKL、PWKL和MPWKL等4个传统选题方法以及新开发的HO-PWKL选题方法.由于MPWKL方法比较耗时,所以本文将采用Zheng Chanjin等[20]提出的预先计算策略来提升MPWKL方法的运行速度.
3.2 被试参数和项目参数的模拟
所需1 000个被试从能力θ服从标准正态分布N(0,1)的集合中随机抽取,每个被试的知识状态α则由HO-CDMs生成.具体来说,通过式(1)计算能力为θi的被试掌握每个属性的概率P(αk=1|θi),然后将此概率和从均匀分布U(0,1)中抽取的随机数u进行比较,若P(αk=1|θi)≥u,则该被试掌握此属性,否则该被试没有掌握此属性.以此类推,最终模拟出被试的真实知识状态.在高阶参数方面,本文采用在已有研究中的参数设定[21-22],所有属性的斜率参数均固定为λ1=1.5;至于截距参数,当属性个数为5时λ0k=(-1.0,-0.5,0,0.5,1.0),当属性个数为8时λ0k=(-1.000,-0.715,-0.430,-0.145,0.145,0.430,0.715,1.000).
本文的题库容量设为500题,每个项目随机测量1~3个属性.根据Ma Wenchao等[23]的建议,从均匀分布U(0.1,0.4)中为每个项目随机生成一个猜测参数P(0)和一个失误参数1-P(1),P(0)表示在被试没有掌握项目测量的任何属性时猜对的概率,P(1)表示在被试掌握了项目测量的所有属性时正确作答的概率.其他知识状态的答对概率从[P(0),P(1)]中随机生成,并满足单调性约束.
给定被试真实知识状态、Q矩阵和项目参数,通过R软件中GDINA包的simGDINA函数[23],为5个属性和8个属性的测试分别模拟一个1 000×500的完全作答矩阵.为消除随机误差,每种模拟实验重复30次,计算30次实验的均值作为最终的实验结果.
3.3 评价指标
3.3.1 模式判准率 模式判准率是评价知识状态分类精度的指标,其值越大则精度越高,计算方法为

3.3.2 能力估计精度 均方差为能力估计精度的指标,其值越小则精度越高,其计算方法为

3.3.3 题库使用均匀性 本文将采用χ2统计量和测验重叠率(test overlap ration,TOR)来衡量题库的安全性,χ2统计量的计算方法为
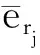
TOR反映不同被试调用相同项目的重叠情况,TOR值越高则题库越不安全.TOR的计算方法为
3.3.4 选题用时 选题方法的运行速度用选择每个项目的平均用时来表示,其计算方法为
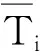
4 实验结果
4.1 实验1:在简化模型下各选题方法的比较
表1为当采用简化模型HO-ACDM时,各选题方法在不同条件下的被试参数估计精度.
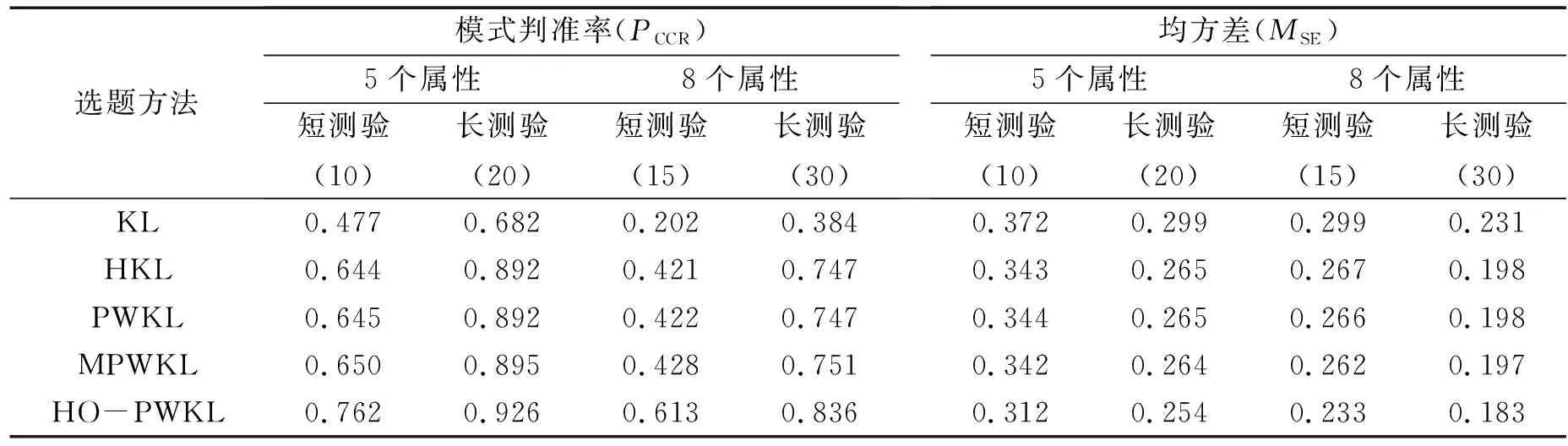
表1 在HO-ACDM模型下各选题方法的被试参数估计精度
在模式判准率(PCCR)方面,当测量5个属性时,新方法HO-PWKL在不同长度测验中的PCCR都高于传统选题方法,这种优势在短测验中尤为明显.如在短测验中,HO-PWKL的PCCR比精度最高的传统选题方法还要高11.2%,而在长测验中,这种差距缩小到3.1%.8个属性的结果与5个属性的结果相似,HO-PWKL的PCCR仍是最高的.不同的是,当属性个数增加时,HO-PWKL在PCCR上的优势更明显.以短测验为例,当测量5个属性时,HO-PWKL与传统选题方法在PCCR上的最小差距仅为11.2%,而当测量8个属性时,这种差距增加到18.5%.这表明:测量的属性个数越多,HO-PWKL在模式判准率上的优势越大.
能力的估计结果与知识状态相似,在不同条件下,HO-PWKL的均方差(MSE)总是最低(即能力估计精度最高),这种优势在短测验中也比较明显.与PCCR不同的是,HO-PWKL和传统选题方法在MSE上的差异并不受属性个数的影响.此外,随着测量属性个数的增加,所有方法的MSE均显著降低,这是因为潜在二分属性在高阶能力估计中的作用类似二分项目,若测量的属性个数越多则高阶能力的估计精度越高[1].在传统选题方法方面,KL的2个测量精度总是最差,HKL、PWKL和MPWKL的测量精度均明显高于KL方法.另外,MPWKL的测量精度与HKL和PWKL相近,这和已有的结果不太一样,其原因可能是采用的模型不同.
表2为各选题方法在长测验中的题库使用均匀性指标.由表2可知:HO-PWKL的曝光率和测验重叠率总是最低.这说明新方法的题库安全性比传统方法更高,而且这种优势不受测量属性个数的影响.在传统选题方法中,HKL和PWKL具有最低且相似的指标,MPWKL的指标较高,KL的2个指标最高,这表明KL的题库安全性最差.
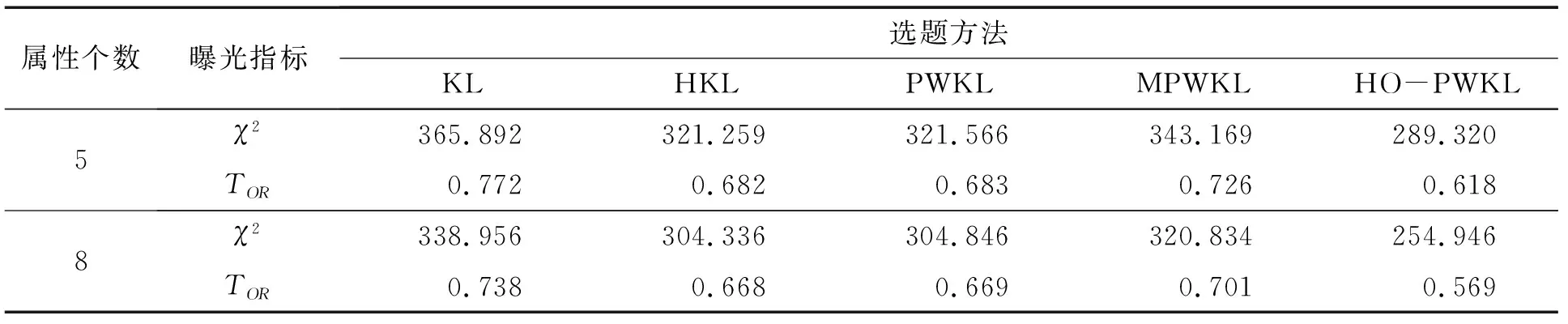
表2 在HO-ACDM模型下各选题方法的题库安全性
实验1的结果表明:在采用简化模型HO-ACDM的Higher-order CD-CAT中,新开发的HO-PWKL的测量精度和题库安全性均优于传统选题方法.这说明新方法是在该CAT系统下较为理想的选题方法.
4.2 实验2:在饱和模型下各选题方法的比较
表3为当采用饱和模型HO-GDINA时,各选题方法在不同条件下的被试参数估计精度,此结果和HO-ACDM的结果非常相似.
由表3可知:HO-PWKL的测量精度依旧最高,其次是MPWKL,再次是非常接近的PWKL和HKL,最差的是KL.与传统选题方法相比,HO-PWKL的PCCR和MSE在短测验中的优势同样突出;同时,若测量的属性个数越多,则HO-PWKL在PCCR上的优势越明显.与HO-ACDM结果不同的是,当采用HO-GDINA模型时,MPWKL的PCCR优于PWKL和HKL的,这和前人的研究基本一致,这说明模型确实会影响选题方法的选题性能.

表3 在HO-GDINA模型下各选题方法的被试参数估计精度
表4为当采用饱和模型HO-GDINA时各选题方法在长测验中的题库使用均匀性指标.HO-PWKL的曝光率和测验重叠率总是最小,这说明HO-PWKL在题库利用上比传统方法更均匀,即题库安全性更高.

表4 在HO-GDINA模型下各选题方法的题库安全性
实验2的结果表明:在采用饱和模型HO-GDINA的Higher-order CD-CAT中,HO-PWKL的测量精度在不同条件下都优于传统选题方法,同时题库安全性也更高.综合来看,不论是饱和模型,还是简化模型,HO-PWKL的测量精度都高于传统选题方法的测量精度,这表明此方法的选题性能不易受模型影响,比较稳定可靠.
表5为各选题方法选择每个项目的平均用时.在所有条件下,KL的选题用时均最少,其次是PWKL和HKL,接着是新开发的HO-PWKL,用时最多的是MPWKL.此结果和预期的结果一致,即方法越复杂,选题用时越多.此外,选题方法的选题用时还与测量的属性个数及题库容量有关.在固定题库容量情况下,属性个数越多,KL类选题方法的选题用时越长,其中MPWKL的选题用时更是呈指数级增长[24].虽然本文采用了预先计算策略[20]提升了MPWKL的计算速度,但当测量的属性比较多时,MPWKL的运算量仍旧非常大,因此选题用时最多.

表5 各选题方法在每题上的平均用时 ms
5 总结与讨论
本文基于PWKL选题思路,结合高阶模型的特性,开发适用于Higher-order CD-CAT、兼顾能力与知识状态的HO-PWKL选题方法.模拟实验的结果表明:在不同条件下,HO-PWKL的测量精度和题库安全性总是高于传统选题方法,尤其是在短测验或测量多个属性时.此外,新方法的优势并不受模型的影响,这表明新方法稳定可靠.在选题用时方面,虽然HO-PWKL的用时比KL、HKL和PWKL更多,但即使在8个属性的测验中,HO-PWKL选择每个项目的平均用时也低于125 ms,这符合CAT的速度要求.综合而言,本文开发的HO-PWKL基本可行,可以满足在Higher-order CD-CAT中兼顾能力和知识状态的选题要求,弥补了传统选题方法的不足.
虽然HO-PWKL的选题也兼顾了能力和知识状态,但它明显不同于传统双目标选题方法.具体而言,由于在Higher-order CD-CAT中的项目不直接提供能力信息[1,8],因此HO-PWKL只考虑由先验和项目提供的知识状态信息以及能力的先验信息;而传统的双目标选题方法,同时考虑了由先验与项目提供的2个潜在变量信息.总之,双目标CD-CAT使用的模型不同(单一模型或分离建模),选题方法的构造也不同[7].
与传统单目标选题方法相比,HO-PWKL的测量精度更高的原因有2个:(i)HO-PWKL在选题过程中考虑了能力信息;(ii)在HO-PWKL下的联合后验概率可能为知识状态提供了额外的信息,即知识状态的条件概率.在题库安全性方面,本文推测被试划分的组数越多,项目的曝光率和测验重叠率就越低.因此,与传统单目标选题方法相比,将被试划分为2K×R个组的HO-PWKL的题库使用均匀性指标更低.在选题用时方面,由于HO-PWKL要计算R次PWKL信息量,因此用时多于KL、HKL和PWKL.但与MPWKL方法相比,随着属性个数增多,HO-PWKL方法仅增加PWKL信息量的运算,而在MPWKL中2K×2K的D矩阵则呈指数级增长,其运算量也呈指数级增加,故而HO-PWKL的选题用时少于MPWKL.
虽然本文开发的新选题方法具有比较理想的测量精度、题库安全性和运算速度,但未来研究还需在以下几方面进一步验证和拓展:首先,本文采用的高阶模型参数和项目参数均假定为真实值,然而在实际中的参数标定不可避免地存在标定误差,其中高阶模型参数的标定误差可能更大[25-26].因此,还需要进一步研究标定误差对HO-PWKL选题性能的影响.其次,由于多维度测量和多级评分项目已广泛应用于心理与教育测验中[27-30],所以,为了推动Higher-order CD-CAT更好地服务实际,有必要开发适用于多维多级的Higher-order CD-CAT选题方法,或者将单维2级的HO-PWKL拓展到多维多级.最后,本文是在定长Higher-order CD-CAT中检验HO-PWKL的选题性能,然而变长Higher-order CD-CAT可能更符合实际需要,即通过不同长度的测验获取相同的测量精度.因此,有必要进一步探究HO-PWKL在变长Higher-order CD-CAT下的测验效率.

