一类带齐次分裂核的群体平衡方程的相似分析及相似解

林府标,王 骞,张千宏

(1.贵州财经大学数统学院,贵州 贵阳 550025;2.贵州师范大学附属中学,贵州 贵阳 550001)

0 引言

群体平衡方程[1-4]广泛应用于实体工业、化学工程、辐射诱导、机械工程、高分子聚合物降解、岩石的破碎、颗粒物的粉磨、药物的粉碎以及液滴、飞沫、微滴、雾滴、云滴的破裂过程等.微滴分裂过程恰好是一分为二的群体平衡方程[1-2],它可写成

(1)

其中x代表微滴的内部坐标,用于描述微滴种类固有的数量性态及特征,如尺寸、形状、孔隙度、质量、体积、长度等;t代表时间,f(x,t)代表在t时刻尺寸是x的微滴分裂的尺寸演化性态分布.分裂核K(x,y)描述尺寸是x+y的微滴分裂成尺寸分别是x和y的速率,并且满足

K(x,y)=K(y,x)≥0,

尺寸是x的微滴分裂的速率v(x)以及尺寸是y的微滴分裂成尺寸是x的平均数量b(x|y)分别定义为

b(x|y)=2K(x,y-x)/v(y).

(2)

b(x|y)满足质量守恒定律,分裂微滴的子代微滴的平均数量满足关系式

(3)

准确理解和应用实体微粒系统的复杂动力学性态以及微粒尺寸演化分布规律,归结为研究方程(1)的精确解[4].但在实体应用领域中,由于缺乏精确求解的理论和方法,因而常用数值技术、矩方法、蒙特卡罗法、类方法、近似解析逼近理论等[1-4].

尺度变换群与量纲分析法常被用于纯微分方程[5-9],文献[8]介绍了量纲分析的理论基础归结于E. Buckingham的π-定理,并且给出了该定理的证明及其在包括1945年的核原子爆炸及热传导问题等纯偏微分方程中的应用.文献[10]探究了多参数尺度变换群的概念及相关理论,给出了单参数尺度变换群在涉及非黏性气体的自相似解等纯偏微分方程中的应用.如今该方法也被用于积分-偏微分方程群体平衡方程[11-18].从纯常微分方程和偏微分方程到积分-偏微分方程和群体平衡方程的应用,并非简单地类推、拓广、平移,这种推广最主要的困难在于积分项及类型的影响.在文献[5-18]的基础上,本文用相似理论研究方程(1)的相似不变量、约化方程、相似解、精确解、解的动力学性态及特征.

1 齐次分裂核与群体平衡方程

设λ和σ为非负实数,σ次齐次分裂核K(x,y)满足

K(λx,λy)=λσK(x,y).

(4)

其中式(4)广泛应用于气溶胶科学、能源科学、医药科学、地球科学等,受到诸多物理学家、化学家、工程师、科学家等的关注[1-4].在数学上易处理的齐次分裂核有K(x,y)=κ0,K(x,y)=κ1(xm+ym),K(x,y)=κ2(xy)n,K(x,y)=κ3|xp-yp|,其中m、n、p和κi(i=0,1,2,3)均是正常数,κi(i=0,1,2,3)代表动力学参数.令y=xs,由式(4)可得

K(x,y-x)=xσK(1,s-1),

K(y,x-y)=xσK(s,1-s),

(5)

针对式(4), 由式(2)和式(5)可得

1-s)/v(y),D(y)=2.

(6)

可验证方程(6)满足式(3).事实上,由式(5)和式(6)可得

因此,将式(4)代入方程(1)可得

(7)

方程(7)的初值和边值条件分别是

f(x,0)=f(x,t)|t=0,f(0,t)=f(x,t)|x=0,f(∞,t)=0.

(8)

f(x,0)=0表示在最初微粒系统中没有微滴存在.f(∞,0)=0描述尺寸足够大的微滴的密度分布趋于0.

2 相似分析

在文献[9-18]的基础上, 用尺度变换群法研究方程(7)的不变量、自相似解、自相似性的可行性.假设方程(7)接受单参数为a的尺度变换群

(9)

其中λ1、λ2和μ是常数,则对于方程(7)的任一解f=f(x,t),需满足

考虑方程(7)接受式(9)的假设,式(9)将方程(7)的任一解f=f(x,t)变成如下方程的解:

(10)

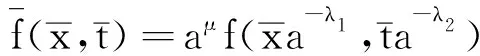
(11)

因为f=f(x,t)是方程(7)的任一解,所以由式(11)可推出

λ2=-(σ+1)λ1.

(12)

用量纲分析和尺度变换群法研究方程(7),且因变量个数m=1,自变量个数n=2,尺度变换群(9)的群参数r=1.于是m+n-r=2,因此存在2个相似不变量

J1(x,t,f)=xω11tω21fω31,J2(x,t,f)=xω12tω22fω32,

(13)

其中ω1i、ω2i、ω3i(i=1,2)为常数.若要式(13)在式(9)的作用下保持不变,则有

依据式(9)和式(13)得到

λ1ω11+λ2ω21+μω31=0,λ1ω12+λ2ω22+μω32=0.

(14)

把式(12)代入方程(14),得到

λ1ω11-(σ+1)λ1ω21+μω31=0,

λ1ω12-(σ+1)λ1ω22+μω32=0.

(15)

3 相似解

类似于式(9),可验证方程(7)接受平移变换群

其中τ0是群参数.若λ1=0,则方程(15)退化成

ω1i,ω2i∈R,ω3i=0(i=1,2).

因此,得到

(ω11,ω21,ω31)T=(1,0,0)T,(ω12,ω22,ω32)T=(0,1,0)T.

(16)

把解(16)代入式(13),得到

J1(x,t,f)=x,J2=(x,t,f)=t.

因此,对于此情形, 借助于Tτ0,方程(7)的相似解可写成

f(x,t)=eα(t+τ)φ(x),α∈R,

(17)

其中解(17)满足式(8),φ(x)满足约化方程

(18)

若λ1≠0,令α=μ/λ1,则α∈R,方程(15)可写成

ω11-(σ+1)ω21+αω31=0,

ω12-(σ+1)ω22+αω32=0.

(19)

方程(19)的解为

(ω11,ω21,ω31)T=(σ+1,1,0)T,

(ω12,ω22,ω32)T=(-α,0,1)T.

(20)

将解(20)代入式(13),得到

J1(x,t,f)=xσ+1t,J2(x,t,f)=x-αf.

因此,借助于Tτ0,方程(7)的相似解可写成

f(x,t)=xαφ(z),z=xσ+1(t+τ0),

(21)

其中解(21)满足式(8),φ(z)满足约化方程

(22)

3.1 情形K(x,y)=κ0

针对K(x,y)=κ0,用性质(4)得到σ=0.由式(17)和式(18)得方程(7)的相似解为

f(x,t)=eα(t+τ0)φ(x),

其中φ(x)满足约化方程

(23)

类似地,由式(21)和式(22)知,方程(7)的相似解可写成

f(x,t)=xαφ(z),z=x(t+τ0),

其中φ(z)满足约化方程

3.2 情形K(x,y)=κ1(xm+ym)

鉴于K(x,y)=κ1(xm+ym),由性质(4)可得σ=m.由式(17)和式(18)知,方程(7)的相似解可写成

f(x,t)=eα(t+τ0)φ(x),

其中φ(x)满足约化方程

类似地,由式(21)和式(22)知,方程(7)的相似解可写成

f(x,t)=xαφ(z),z=xm+1(t+τ0),

其中φ(z)满足约化方程

3.3 情形K(x,y)=κ2(xy)n

针对K(x,y)=κ2(xy)n,由性质(4)可得σ=2n.由式(17)和式(18)知,方程(7)的相似解为

f(x,t)=eα(t+τ0)φ(x),

其中φ(x)满足约化方程

类似地,由式(21)和式(22)知,方程(7)的相似解可写成

f(x,t)=xαφ(z),z=x2n+1(t+τ0),

其中φ(z)满足约化方程

3.4 情形K(x,y)=κ3|xp-yp|

对于K(x,y)=κ3|xp-yp|,由性质(4)可得σ=p.由式(17)和式(18)知,方程(7)的相似解可写成

f(x,t)=eα(t+τ0)φ(x),

其中φ(x)满足约化方程

类似地,由式(21)和式(22)知,方程(7)的相似解可写成

f(x,t)=xαφ(z),z=xp+1(t+τ0),

其中φ(z)满足约化方程

4 精确解及动力学性态

方程(7)的精确解对理解微粒系统的动力学性态、理论和实际应用都是有价值和意义的.采用尺度变换群法能否获得方程(7)的精确解,归结为对约化方程的精确解的研究问题.针对K(x,y)=κ0,方程(7)可具体写成

(24)

用观察试探函数法[11-18],可验证φ(x)=(κ0x+α)-3是方程(23)的解,因此,方程(24)的精确解为

f(x,t)=(κ0x+α)-3eα(t+τ0).

(25)

假设f=f(x,t)是方程(24)的解,且满足式(8),则0阶矩M0(t)和1阶矩M1(t)分别为

其中M0(t)表示在微粒系统中微滴的总数量,M1(t)表示在微粒系统中微滴的总质量.若微滴在分裂过程中总保持质量守恒,则M1(t)是时间t的不变量,即满足dM1/dt=0.方程(24)两边关于变量x从0到∞同时积分,得到

(26)

采用M0(t)和M1(t)及式(26),可得

dM0/dt=κ0M1.

(27)

解(25)是方程(24)的真实解,将它满足的动力学性态逐一进行分析.当x→∞时,f(x,t)→0,这表明微滴的密度函数满足性质:当微滴尺寸足够大时,微滴的密度函数值趋于0.若参数α>0,则当t→∞时,可推出f(x,t)→∞,这表明解是不稳定的;若参数α<0,则当t→∞时,可推出f(x,t)→0,这表明解是稳定的;若参数α=0,则微滴的密度函数f(x,t)是时间t的不变量,满足∂f(x,t)/∂t=0,这表明微滴因分裂而出生与微滴因分裂而死亡保持平衡.解(25)对应的初值和边值条件分别为

f(x,0)=(κ0x+α)-3eατ0,f(0,t)=α-3eα(t+τ0),f(∞,t)=0.

假设L、T为正常数,在闭矩形区域[0,L]×[0,T]上,对应的初值和边值条件分别是

f(x,0)=(κ0x+α)-3eατ0,f(0,t)=α-3eα(t+τ0),f(L,t)=(κ0L+α)-3eα(t+τ0).

考虑解(25),M0(t)和M1(t)及其相应的变化率分别为

dM0/dt=eα(t+τ0)/(2κ0α),

M0(t)和M1(t)及其变化率的计算结果表明:解(25)满足M0(t)的变化率与M1(t)的性质(27).若参数α>0,则变化率dM0/dt>0,这表明在微粒系统中随着微滴分裂的不断演化,微滴的总数量不断增加,出生的比死亡的更多;若参数α<0,则变化率dM0/dt<0,这表明在微粒系统中随着微滴分裂的不断演化,微滴的总数量不断减少,死亡的比出生的更多.变化率dM1/dt>0表明在微粒系统中随着微滴分裂的不断演化,微滴的总质量不守恒,且是非单调递减的.本文分别选取参数α=0.6和α=-1.5,τ0=0,动力学参数κ0=0.8和κ0=3.1,微滴分裂演化的动力学性态和微滴的密度函数式(25)在矩形区域[0,2]×[0,0.8]上的图像分别如图1(a)和(b)所示.

(a)κ0=0.8,α=0.6,τ0=0 (b)κ0=3.1,α=-1.5,τ0=0图1 微滴尺寸分布分裂演化行为函数式(25)的图像

5 结束语

用尺度变换群法研究方程(7)的相似分析,不仅是有效的,而且构造了相似不变量、约化方程、精确解,分析了精确解的动力学性态及特征.如何构造解析求解的方法探寻约化方程的精确解,并且给出原方程的精确解及动力学性态分析,这些都值得在今后的研究工作中不断创新.