伺服电机电磁参数测量与弱磁控制电流工作点优化方法

陈洪赟，阎 彦,2，林治臣，曹彦飞，史婷娜,2

(1.浙江大学电气工程学院，浙江 杭州 310027；2.浙江大学先进电气装备创新中心，浙江 杭州 311107)

1 引言

伺服电机系统是机械臂、数控机床等精密制造、加工装备的核心运动部件，持续提升伺服电机系统的运行品质水平、精度保持性等，对于我国制造业提质升级具有重要意义[1，2]。

机械臂、数控机床等装备中的伺服电机多为表贴式永磁同步电机，在基速以下运行时，常采用直轴电流为零的控制方式，该方式下交轴电流与电磁转矩成正比，且电机运行中铜耗最小；基速以上运行时，一般以速度最大化为目标，为在有限的电压、电流给定情况下尽可能扩大电机速度范围，弱磁控制策略是实现上述需求的有效方法。然而，受温升、磁饱和等因素影响，在宽速域运行下的伺服电机参数可能会有较大程度的变化。对此，为应对参数非线性时变对电机弱磁区运行转矩输出能力的影响问题，直、交轴电流工作点的优化选取极为重要[3，4]。

目前，实现弱磁控制下交直轴电流给定的在线方法有电压反馈法[5-7]、在线模型计算法[8-12]和先验数据查表法[13-15]。电压反馈法通过增加一个电压环反馈实现弱磁电流的控制，该方法简单有效，并且不依赖参数，但无法实现最大转矩电压比的控制[7]。在线模型计算法的核心在于：①利用有限元计算结果或实验测量数据，建立电机交直轴电感、永磁磁链随交直轴电流变化的数据模型；②建立弱磁区电流工作点与转矩、磁链、供电电压间的数学关系模型。借助以上模型，电机参数与弱磁运行工作点互为输入、输出，反复迭代计算，当前后两次迭代计算的两组交直轴电流参考值间的绝对误差小于容许误差时，即可实现工作点定位[11，12]。先验数据查表法将离线实验测得的电感参数或电流给定值存储为表格形式，在电机运行过程中通过检索表格获取工作点。通常，查表法有两种方式，第一种是记录电机不同电流下的电感参数[13]，每个控制周期中通过查表更新电机参数后辅助在线控制算法进行电机运行区控制。第二种是离线制定给定电流和给定转矩、给定转速的关系表，在控制过程中直接查表得到给定电流进行控制[14，15]。

纵观上述方法，从应用现状来看，离线获取交直轴电流-转矩-转速间先验数据的制表方法应用最为广泛。该方法的核心——先验数据表，其获得方式可分为有限元仿真和离线测量两种，主要局限在于：①查询表中数据的准确性与有限元仿真步长和先验实验测量的精度有着密切的联系；②离线测量查表法通过穷举电机的各个工况，来得到电机不同运行区的精确电流给定，需要花费大量时间。

近年来，有学者提出了在测量堵转电机电感和转矩参数后计算查找表的方法[15]。该方法在堵转工况下，将电机直接连接在电压源，借助电机引出的中性点，测量电机磁链和转矩数据，从而计算给定电流。在该思路基础上，本文针对带制动器的伺服电机提出一种弱磁运行区查找表计算的新方法。区别于文献[15]，所提方法直接利用伺服电机驱动器离线测量堵转时的伺服电机电压、电流、位置、转矩数据；进一步在实测数据基础上建立磁链和转矩关于电流幅值和电角度的拟合式；最后，利用拟合式实现不同转子位置、转矩、转速下伺服电机最优给定交直轴电流的优化设定。

2 伺服电机转矩、磁链离线测量

图1 离线测量时伺服驱动器控制结构简图Fig.1 Control structure diagram of servo driver during off-line measurement

2.1 测量原理

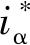
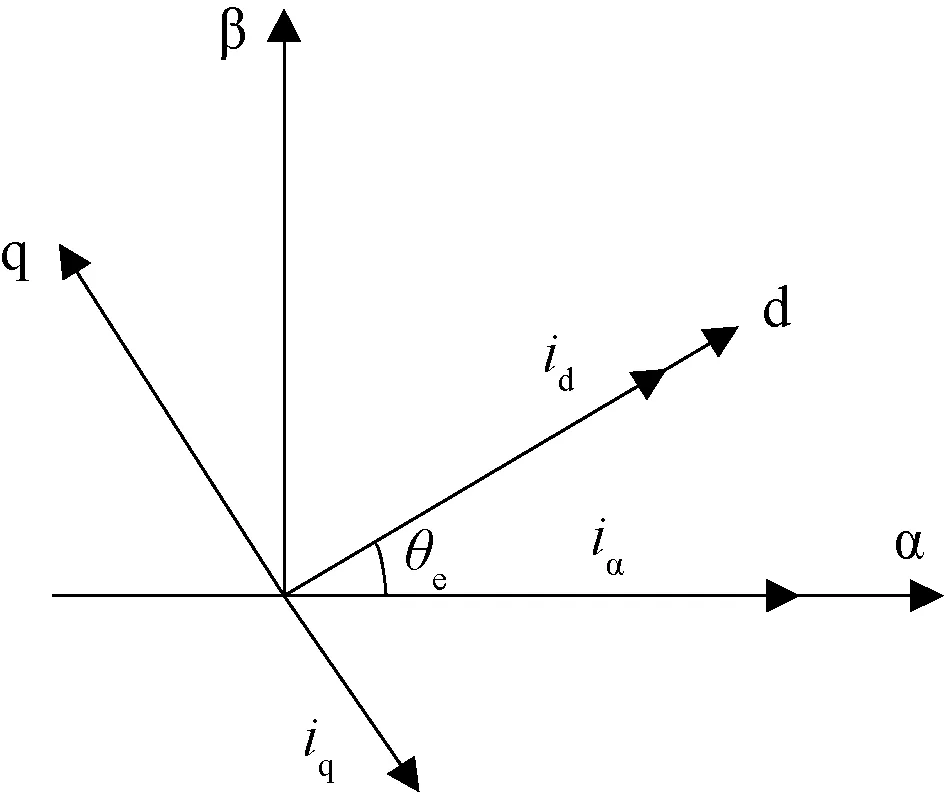
图2 电流分量关系图Fig.2 Current component diagram

由于控制β轴电流为0，因此有：

(1)

式中，id和iq为d-q坐标系下电机定子电流分量。

电机在α-β坐标系下电压方程为：

(2)

式中，vα和vβ、ψα和ψβ依次为α-β坐标系下电机定子电压分量、定子磁链分量；Rs为定子电阻。用欧拉法可以得到电机的磁链积分式：

(3)

式中，ψα1和ψβ1分别为永磁磁链在α-β轴的磁链分量；ψα2和ψβ2分别为α-β轴电流产生的磁链。

利用式(3)可以得到不同电流下的ψα2和ψβ2，进一步结合伺服电机编码器位置信息和旋转坐标变换，可以转换成d-q坐标系下电流产生的磁链分量，即：

(4)

式中，ψd和ψq分别为永磁磁链在d-q轴的磁链分量。

采用上述方法测量并计算在同一电角度位置下、不同电流幅值下电机的交、直轴磁链分量；与此同时，利用转矩传感器测量同条件下的电机输出转矩。旋转电机以改变θe，进一步测量、计算不同电流幅值、不同电角度位置下的电机磁链和转矩，形成先验数据表。

需要说明的是，相比于文献[15]将电机三相直接连接电压源，本文所提测量方法通过加入控制形成电流闭环，能够保证计算的磁链是给定电流工况下的磁链，并且电流能够更快地到达给定电流，减小了温度变化对于电机电阻的影响，有效减小了积分时的误差。

2.2 测量过程中驱动器死区电压补偿方法

由于逆变器非线性和死区的影响，电机的实际电压与给定电压会有差异，故在式(3)的积分计算中需要对给定电压进行补偿。被测电机运行在iα>0、iβ=0的稳态时，根据逆Clarke变换，有：

(5)

在稳态下，电压关系同电流关系，其等效电路如图3所示[16]。

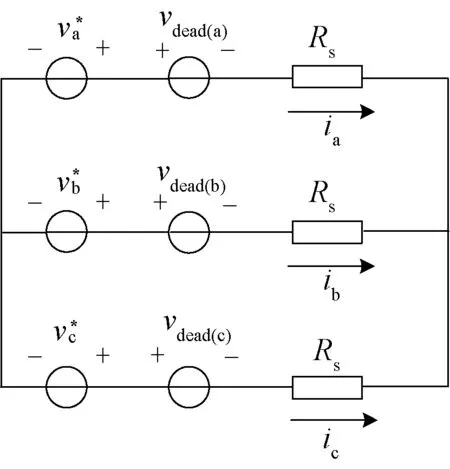
图3 稳态下电机等效电路Fig.3 Motor equivalent circuit under steady state

根据基尔霍夫电压定律，有：

(6)

在只考虑死区的非线性影响时，有：

(7)

式中，Vdead为由于死区产生电压压降的幅值；x={a,b,c}。将式(7)代入式(6)中，结合式(5)有：

(8)

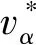
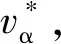
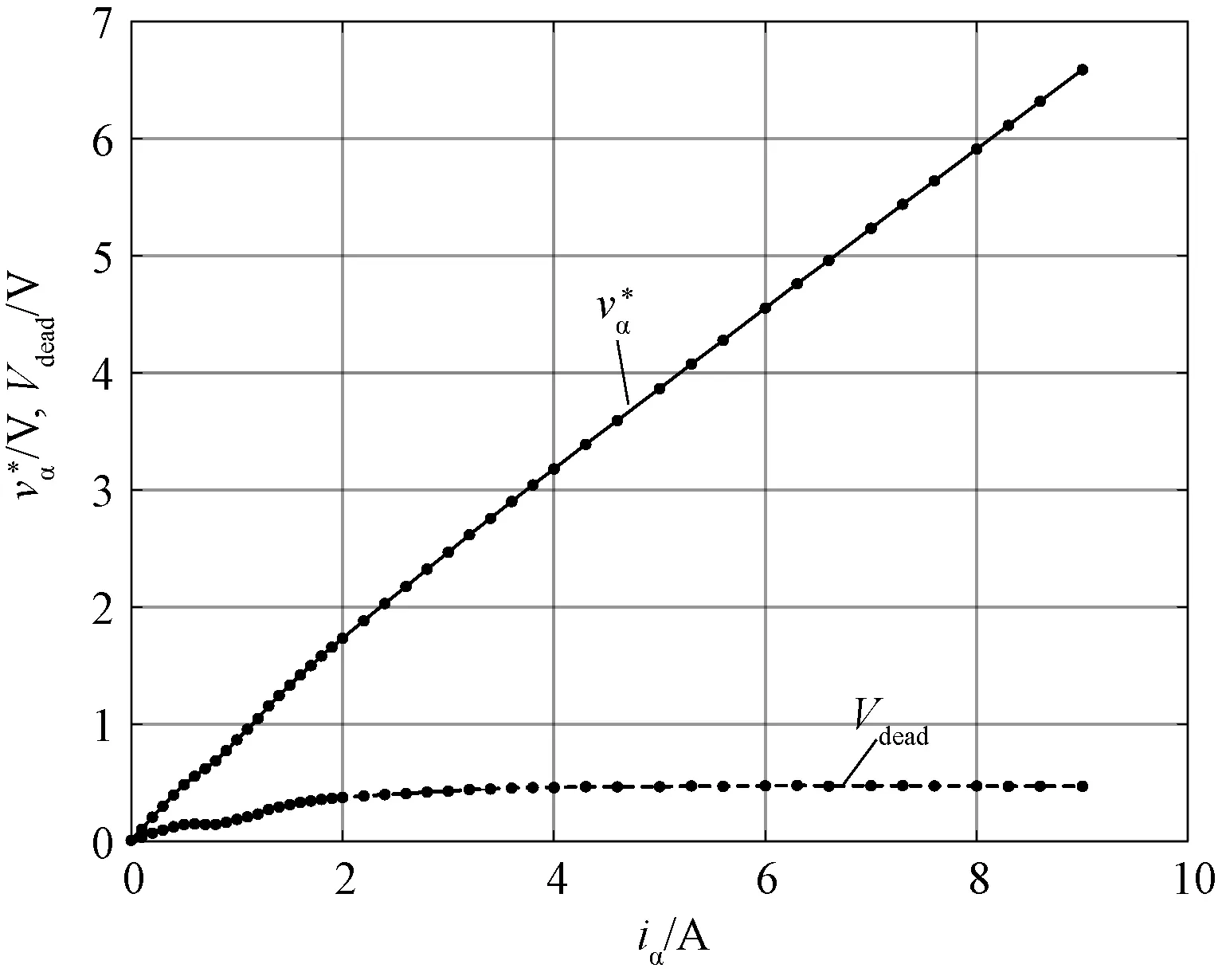
图与Vdead随iα的变化关系Fig.4 Relationship between and Vdead with iα

由图4中可以看出，当iα较大时，实线斜率趋近于稳定，根据式(8)，实线的斜率即为定子电阻Rs；当iα较小时，Vdead近似为线性变化；当iα较大时，Vdead数值趋于稳定，可视为恒值。

(9)

3 伺服电机转矩、磁链数据拟合

在离散电角度和离散电流下的磁链和转矩数据基础上，利用傅里叶级数拟合方法，能够建立磁链、转矩模型如下：

(10)

式中，φdn(Is)、φqn(Is)、φtn(Is)分别为iα在阶段性稳态(稳态电流用Is=[0,Imax/n,2Imax/n,…,Imax] 表示)下的直轴磁链、交轴磁链、转矩的傅里叶级数系数；h为拟合时的最大谐波数；φyn(Is)可由式(11)拟合：

(11)

式中，y={d,q,t}；ad(n,j)、aq(n,j)、at(n,j)分别为直轴磁链、交轴磁链、转矩的多项式系数；g为拟合多项式的最大次数。

由此可得磁链和转矩关于电流幅值和电角度的拟合式为：

(12)

式中，I为任意电流幅值；θ为电机任意电角位置。

式(12)直观地表现了磁链和转矩与电流之间的关系，由此可以求得不同电流幅值、不同转子位置下的电机磁链和转矩。由于电流幅值I和电角度θ并不耦合，磁链和转矩对于电流幅值和电角度的偏导数也较容易获得。

4 伺服电机弱磁区电流工作点求解

弱磁区内，最优电流工作点为电压极限椭圆与恒转矩曲线的交点。结合输出转矩等于给定转矩，因此最优给定电流的方程组为：

(13)

由于ψd(I,θ)、ψq(I,θ)、Te(I,θ)是复杂的关于电流幅值和电角度的函数，直接计算方程组(13)比较困难。牛顿法是一种收敛速度快的非线性方程解法，它要求方程是连续的并且存在连续的偏导数[17，18]。下面利用式(12)所示磁链和转矩的表达式连续且其偏导数连续的特性，利用牛顿法对方程组(13)进行求解。牛顿法的解迭公式为：

(14)

式中，f1和f2为关于I和θ的方程；k为迭代的次数；J为f1和f2对I和θ的雅可比矩阵。

对于式(13)，设：

(15)

其雅可比矩阵为：

(16)

式中，F1，F2分别为函数f2对I和θ的偏导数，有：

(17)

(18)

当迭代的误差小于设置精度ε时，有：

(19)

即可得到弱磁区运行时交直轴电流工作点。

5 实验结果与分析

为了证明所提方法有效性，在一台西门子伺服电机上进行了实验，被测电机参数见表1。

搭建实验系统如图5所示，实验系统由被测电机、直流电源、逆变器、基于DSP(TMS320F28335)和FPGA(EP1C6Q240C8)的核心控制器、电流传感器(LH 25-NP)等构成。实验系统控制频率和载波频率为10 kHz。

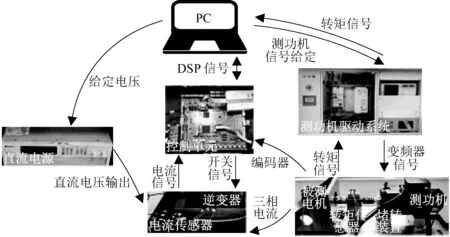
图5 实验系统图Fig.5 Diagram of experiment system

对于第2节所述测量阶段，稳态电流Is从2 A开始，间隔2 A，直到达到20 A；电角度θe从90°开始，间隔15°，直到270°；实验测量得到的转矩和磁链、以及用第3节所述方法拟合得到的转矩和磁链如图6所示。

图6 交直轴磁链、转矩测量与拟合结果Fig.6 Measurement and fitting results of d-q axis flux linkage and torque

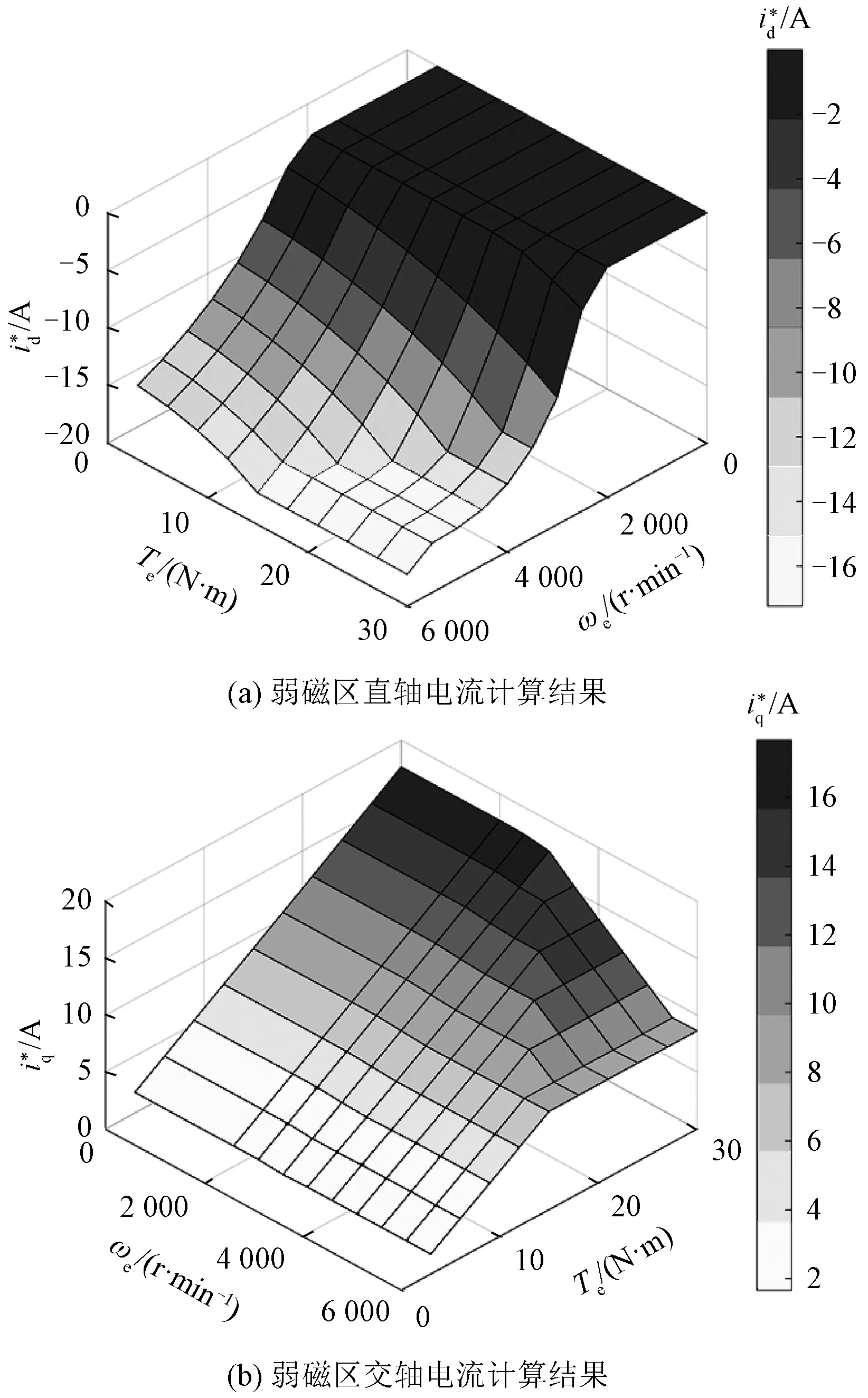
图7 弱磁区交直轴电流计算结果Fig.7 Calculation results of d-q axis current in flux weakening region

6 结论

本文提出了一种伺服电机转矩、磁链测量以及弱磁运行区工作点计算方法。该方法分为电机磁链、转矩参数测量，测量参数曲面拟合和查找表电流求解三个步骤。在测量过程中，通过加入控制形成电流闭环，使电流快速到达给定值，减少温度变化引起的电阻压降及其对磁链积分误差的影响。同时在控制算法中对驱动器死区进行了补偿，抵消了驱动器死区效应对测量结果的影响。所提方法对带有制动器的伺服电机有很好的适用性，通过制动堵转-位置控制下微小角度旋转-制动堵转间的切换，即可测量并计算出伺服电机弱磁区运行的交直轴电流工作点，具有易于集成在伺服电机驱动器内部的优势。