非接触式驱动方式的超导钉扎磁浮悬浮-导向-驱动综合性能研究
李 静,郑 珺,罗 奕,张思涵
(1.西南交通大学电气工程学院,四川 成都 610031;2.西南交通大学牵引动力国家重点实验室,四川 成都 610031;3.磁浮技术与磁浮列车教育部重点实验室,西南交通大学,四川 成都 610031)
1 引言
磁浮技术的发展为未来交通运输方式提供了一种新的可能。其中,高速磁浮列车拥有良好的发展前景,具有速度高、噪声小、绿色环保等优势[1,2]。
目前,在工程化应用的高速磁浮线路[3-5]中,驱动系统以直线电机为主。真空管道高温超导钉扎磁浮车“Super-Maglev”[6]的驱动系统采用直线感应电机;620 km高温超导钉扎高速磁浮工程化试验线利用直线同步电机实现推进。从现有工程化磁浮实例可以看出,为了实现高速磁浮列车速度的全线路可调,直线电机一般采用沿线路铺设三相绕组的方式,这会为磁浮系统带来工程造价水平高的问题。杜一星等人[7]从直线电机原理出发,提出利用永磁轨道磁场与车载直流线圈间的电磁作用实现驱动的方案,并通过理论推导、有限元仿真以及实验验证了该方案的可行性。基于该驱动方案的高温超导钉扎磁浮系统利用同一磁轨磁场与高温超导材料的“钉扎”作用以及与通电线圈的电磁作用分别实现了垂向悬浮、横向导向以及纵向驱动,巧妙达到了驱动系统与悬浮-导向系统的有机结合。但是,目前用于验证此驱动方案的高温超导钉扎磁浮系统在同一磁轨条件下不能同时实现悬浮力、导向力和驱动力俱优。
日本低温超导电动磁浮[8]通过为“8”字形悬浮-导向(Levitation-Guidance,LG)线圈叠加牵引电流的方式改进线圈结构,提出利用车辆上的超导磁体与安装在导轨侧壁上的驱动-悬浮-导向(Propulsion-Levitation-Guidance,PLG)线圈[5,9]产生的磁力运行,实现了悬浮、导向、驱动一体化功能。Halbach永磁阵列是由美国科学家K.Halbach[10]提出的,能够使用最少量的永磁材料产生较强的磁场,广泛应用于永磁电机、磁浮交通等各个领域。张威风等人[11]通过优化永磁体的尺寸和磁化角,提高了高温超导钉扎磁浮系统的悬浮-导向性能。因此,针对新型高温超导钉扎磁浮系统悬浮-导向-驱动综合性能较弱的问题,本文在保持系统悬浮、导向性能良好的前提下,通过优化原Halbach永磁阵列的磁化角,得出三种新型永磁轨道排列方式。通过仿真对比磁场强度、电磁力验证了改进方法的有效性。该研究为永磁轨道的进一步优化及高温超导钉扎磁浮悬浮、导向与驱动一体化技术的发展提供参考。
2 新型高温超导磁浮车系统
国内外所有高温超导钉扎磁浮车轨都是由永磁磁轨、车载超导块材以及直线电机组成。车载超导块材一般为采用熔融织构法制备的圆柱形或者方形高温超导 YBaCuO块材,YBaCuO块材放置于车载低温杜瓦中,共同构成车载悬浮体。轨道一般为由NdFeB永磁体和聚磁铁轭按一定的结构组装而成的磁场浓缩型 Halbach 永磁阵列。直线电机驱动系统由感应或者同步直线电机及其控制系统构成。本文保留高温超导磁浮系统车载悬浮体的结构,同时利用永磁轨道与线圈的电磁作用实现驱动作用,并将此驱动方式称之为非接触驱动方式。
2.1 非接触式驱动原理
由安培力定律[12]可知,在磁场中有电流强度为I的线电流回路,则磁场对该电流回路的作用力为:
(1)
式中,N1为线圈的匝数;B为磁感应强度;I为单匝线圈电流。
线圈磁场、磁轨磁场、铁心磁化磁场叠加后形成的复合磁场在空间内呈三维分布。不妨假设空间任一点的磁感应强度为(Bx,By,Bz),结合安培力定律得出单匝线圈产生的安培力为:
(2)
其中驱动力为:
(3)
因为磁场是无源有旋场,故磁场强度的散度可以表示为:

(4)
由于单匝线圈投影域为平面闭区域,且复合磁场的磁感应强度分量By、Bz具有一阶连续偏导数,利用格林公式,联立式(2)、式(3),推及整个三维线圈结构,可得非接触驱动产生的驱动力表达式为:
(5)
在异型线圈附近增设和布置铁磁性磁场调控件,即导磁片,以改变通电线圈所处磁场的磁场强度的纵向梯度。从而使线圈下端磁场纵向分量波动增强而产生推力。
2.2 新型高温超导磁浮系统
高温超导钉扎磁浮车系统是一种无需主动控制、无需电源激励的自稳定悬浮系统,主要由车载超导块材及其低温系统、驱动系统和地面轨道系统组成。永磁轨道沿线路铺设于地面,采用双轨结构。低温系统为高温超导块材提供保温作用,有效增加块材处于超导态的时长。图1是基于非接触式驱动的高温超导钉扎磁浮列车概念示意图。新型钉扎磁浮系统利用永磁轨道磁场与高温超导块材之间的磁通钉扎作用实现悬浮-导向耦合,场冷超导体内部的感应电流保证了垂直方向上的悬浮稳定性,而俘获磁通则保证了悬浮的侧向稳定性。驱动系统主要由永磁轨道、双闭口异型线圈、铁磁片构成。线圈采用多匝形式。结合新型非接触式驱动方式,在同一磁轨条件下能够产生俱优的悬浮、导向与驱动性能。
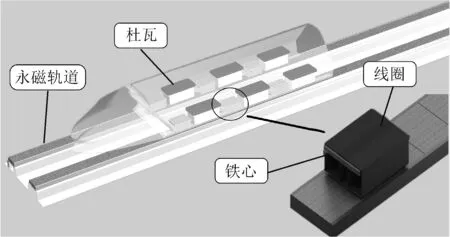
图1 新型高温超导钉扎磁浮列车概念示意图Fig.1 Novel HTS flux-pinning maglev train
本文研究中的杜瓦作为独立保温装置,非接触式驱动线圈与杜瓦固定,二者共同安装于列车底部,分别利用前后两侧磁场通过电磁作用将杜瓦与非接触式驱动线圈联系起来,因此,杜瓦与非接触式驱动之间能够实现自然解耦,因此可独立分析新型高温超导磁浮系统中的悬浮-导向子系统与非接触式驱动系统。
3 新型高温超导磁浮车系统
将原Halbach永磁轨道(Permanent Magnet Track,PMT)两侧横向磁化的永磁体替换为任意角度磁化的永磁体,利用FEMM软件筛选出能够产生对称磁场[13]的磁轨排列方式,筛选出的三种磁轨排列方式及其磁场分布如图2所示。

图2 产生对称磁场的磁轨排列方式Fig.2 PMT arrangement producing symmetrical magnetic field
4 悬浮-导向性能研究
4.1 超导钉扎磁浮基本模型
在Comsol Multiphysics平台上对具有明显非线性E-J特性的超导体进行时域磁场建模[14-17]。基于现有高温超导磁浮环形试验线“Super-Maglev”的悬浮-导向系统建立本文高温超导钉扎磁浮基本系统模型。
首先,根据永磁轨道和超导块材的实际尺寸,搭建永磁轨道、超导块材、动网格域等基本模型。采用幂指数模型[18]来描述超导体的E-J特性:
(6)
式中,Ez为电场强度;J为超导体的电流密度;n为幂指数,取值21;E0由超导材料和温度决定,取值为1×10-4V/m;Jc为临界电流密度,Jc=1.1×108A/m。
在仿真模型全局变量中定义E0、Jc。在AC/DC模块磁场公式物理场中,选择E-J特性作为超导块材的传导特性,并设置永磁体和超导块材的材料属性参数,其中构成永磁轨道的永磁体剩余磁通密度为1.2 T。然后,定义高温超导块材下表面到永磁轨道上表面的距离为悬浮高度,高温超导体场冷进入超导态时的高度为场冷高度。以原Halbach永磁轨道的超导磁浮模型为例,有限元仿真工况[19]如图3和图4所示,场冷高度为30 mm[20],车载超导体下降20 mm到达工作高度,然后上升20 mm至场冷高度,计算垂向运动中的悬浮力。其次,在工作高度10 mm处,超导体左右偏移10 mm作横向运动,计算横向运动中的导向力。
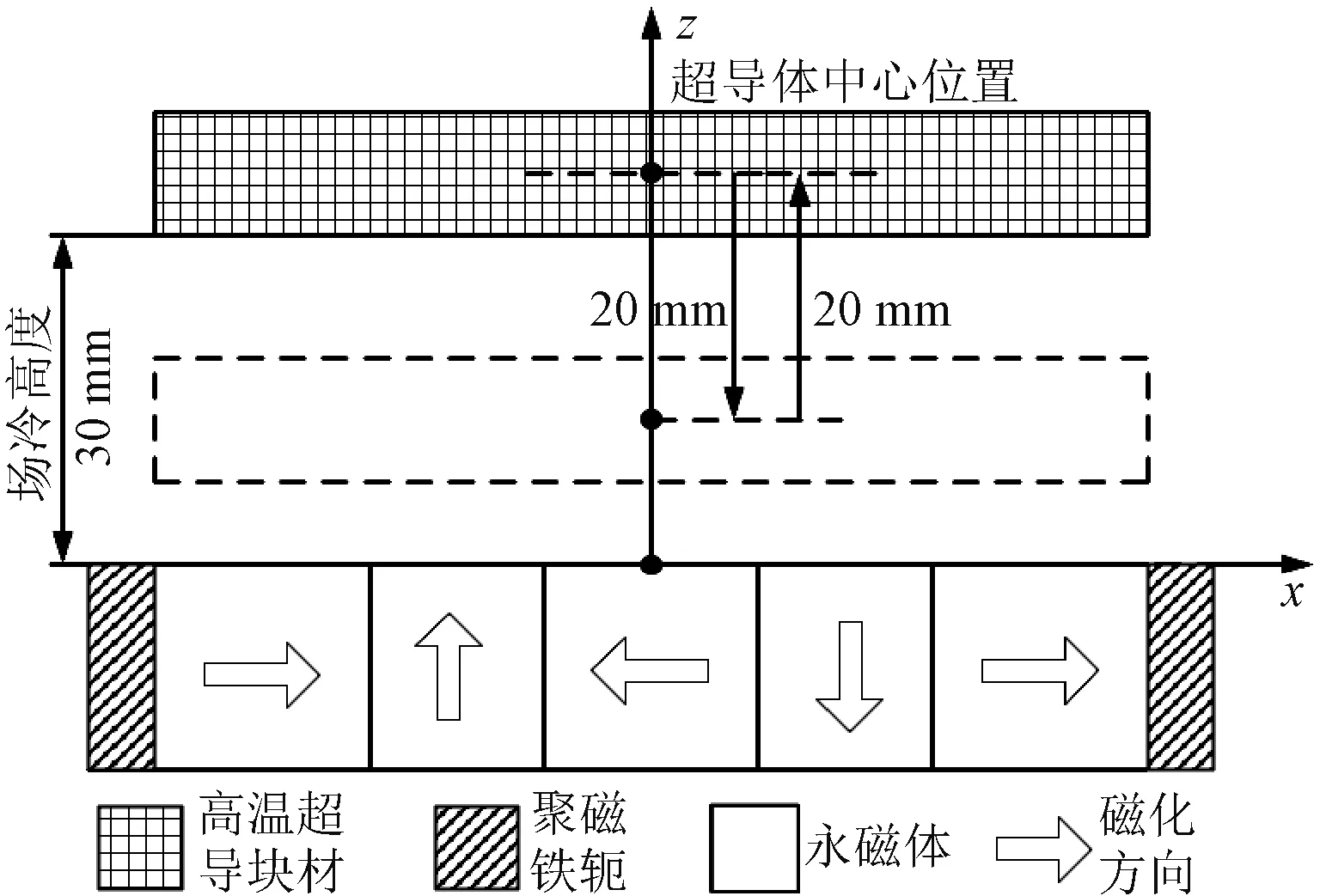
图3 悬浮力仿真工况Fig.3 Simulation condition for levitation force
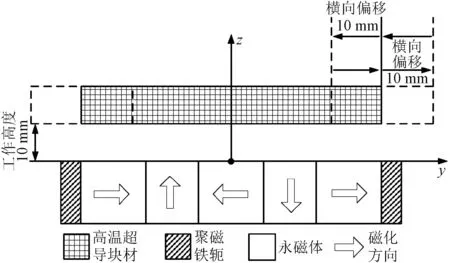
图4 导向力仿真工况Fig.4 Simulation condition for guidance force
永磁轨道在垂向运动过程中始终保持与车载高温超导体中心对齐,在横向运动过程中始终保持与车载高温超导体平行。添加动网格物理场,定义横向、垂向运动工况,从而完成实际工况的仿真设置。
最后,在仿真定义中添加全局变量探针,提取电磁力密度,并对高温超导块材区域进行积分。由式(7)计算出该过程超导体受到的悬浮力,由式(8)计算出该过程受到的导向力。
(7)
(8)
式中,Jx为Bx、By垂向上的电流密度;Bx、By分别为磁感应强度的水平分量和竖直分量;S为超导体在yoz平面求解域面积。
4.2 磁场分析
除了永磁体的磁化角不同外,新型永磁轨道的总体尺寸及剩磁大小与原Halbach轨道完全相同。其上方10 mm高度处的磁场强度对比如图5所示。
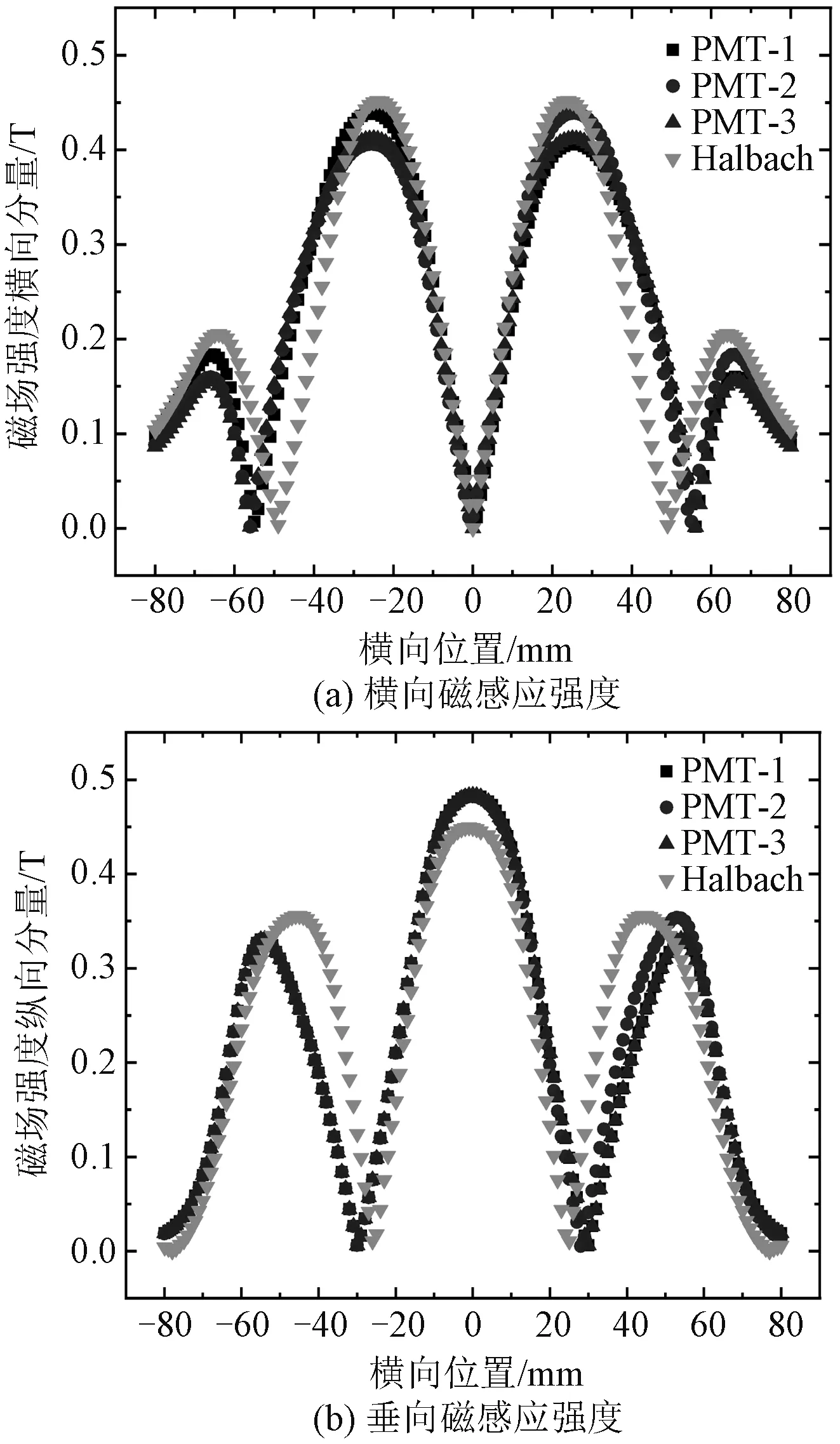
图5 四种磁轨上方磁场的比较Fig.5 Comparison of magnetic field above four kinds of PMT
对于横向磁场,新型永磁轨道最大值达到了0.48 T,而原Halbach轨道横向磁场By的最大值为0.44 T;而且在横向宽度50~100 mm这一范围内,新型轨道的横向磁场始终高于原Halbach轨道,在这一范围外,略低于原Halbach轨道。对于垂向磁场,在横向宽度65~95 mm这一范围内,新型轨道的垂向磁场与原Halbach轨道一致,只有在边缘很小的宽度范围内略低于原Halbach轨道。综合比较四种轨道上方的横向磁场|By|和垂向磁场|Bz|可知,新型永磁轨道能够提供与原Halbach轨道强度相当的磁场。
4.3 超导磁浮悬浮-导向力学特性
与“Super-Maglev”系统的Halbach永磁轨道相比较,得出高温超导钉扎磁浮基本系统的悬浮及导向特性如图6所示。
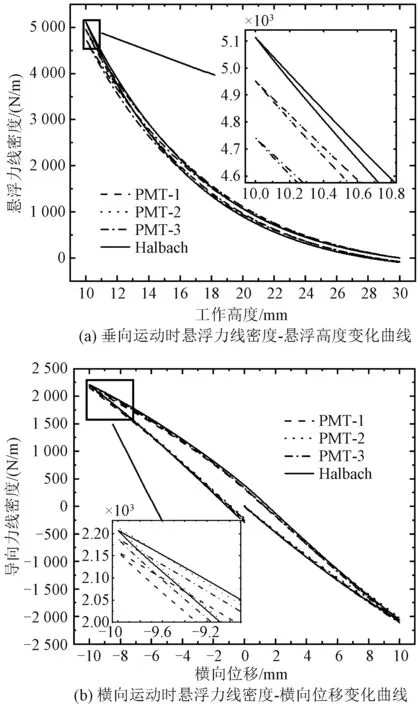
图6 高温超导钉扎磁浮悬浮及导向特性对比图Fig.6 Comparison of levitation and guidance characteristics of HTS maglev
从图6(a)可以看出,块材下降至最低点时悬浮力密度最大,三种新型磁轨(PMT-1、PMT-2、PMT-3的悬浮力密度最大值分别为4 951.3 N/m、4 951.3 N/m、4 740.5 N/m,相对于原Halbach,三种新型磁轨的悬浮力密度分别仅降低了3.1%、3.1%、7.3%,新型永磁轨道的最大悬浮力虽然密度略低于原Halbach,但基本与原Halbach的悬浮力密度接近。从图6(b)可以看出,三种新型磁轨(PMT-1、PMT-2、PMT-3)的导向力密度最大值分别为2 158.8 N/m、2 213.7 N/m、2 188.5 N/m,而原Halbach的导向力密度为2 207.5 N/m。相对于原Halbach,导向力密度变化了-2.2%、0.28%、-0.85%(“-”表示减低、“+”表示提高),在误差允许范围内,新型永磁轨道的最大导向力密度基本与原Halbach一致。
逝者满七后,紫云探望师母。那天,雨心的心情很糟,紫云请她出去走走。在大街上碰到了蒋浩德,一起到附近的茶馆坐一下。
通过对悬浮力、导向力的分析,可以看出,基于新型永磁轨道的高温超导钉扎磁浮系统能够产生与原Halbach磁轨近似的悬浮力、导向力,载重能力能够满足日后应用需求。
因此,在保证具有较好悬浮力、导向力的条件下,本研究能够利用相同磁轨条件进一步叠加铁磁片研究驱动力性能,
5 驱动性能研究
5.1 驱动仿真模型的验证
5.1.1 实验扫描原Halbach磁轨磁场
磁场的测量采用三维磁场扫描测试平台开展磁场数据的采集工作。三维磁场扫描测试平台由三维扫描系统、数据采集系统和显示器组成,如图7所示,可以实现三个维度的磁场扫描。如图7(b)所示,实验仅扫描两个维度的磁场,当扫描磁场水平分量时,y轴电机运动(霍尔传感器水平放置);扫描不同高度时,z轴电机运动。
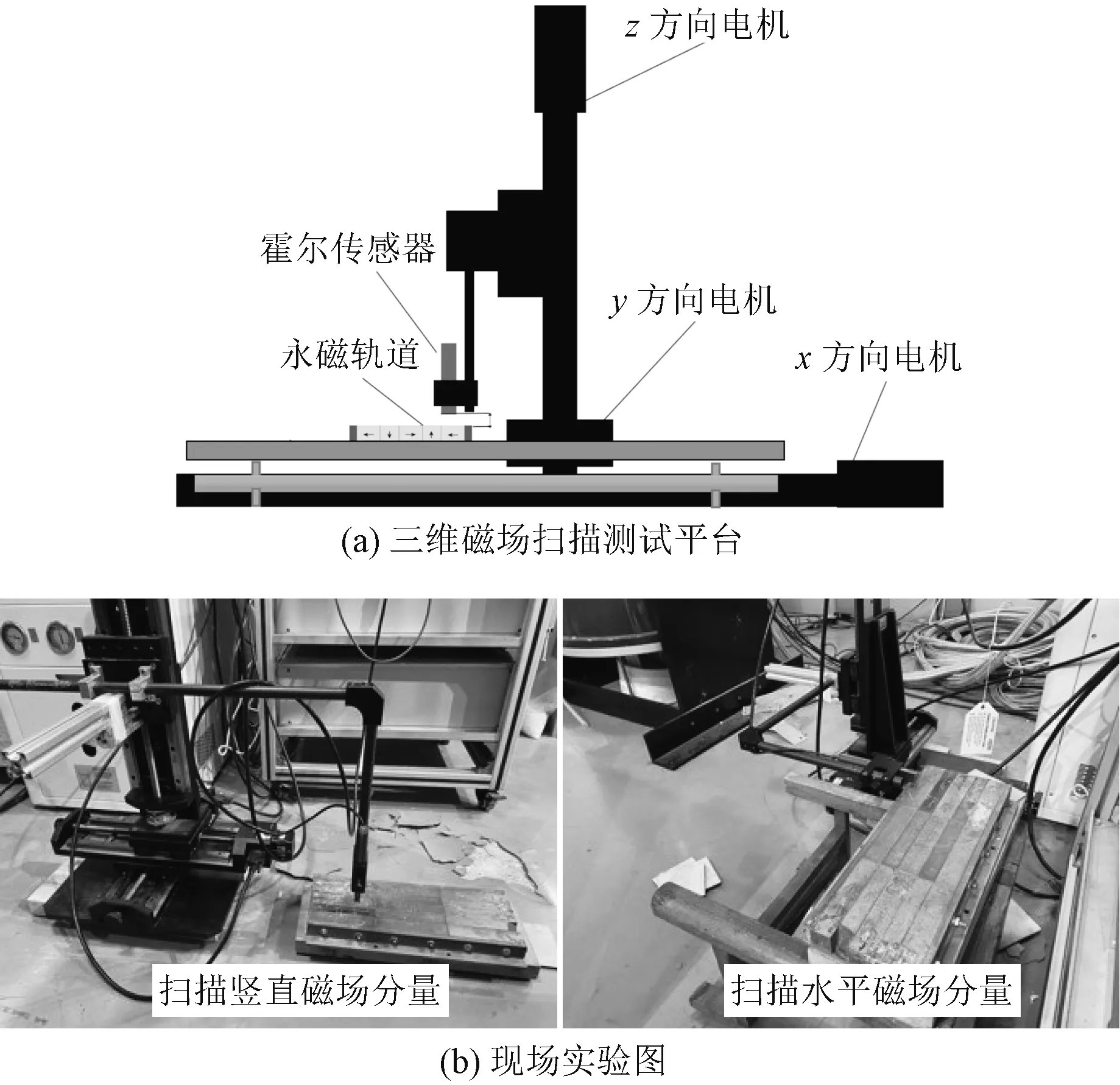
图7 磁轨磁场扫描实验Fig.7 Scanning experiment of magnetic track magnetic field
5.1.2 输出磁场数据
在ANSYS Maxwell电磁场仿真软件中建立无铁心非接触式驱动结构的三维静磁场模型[21]。为避免线圈与永磁轨道之间发生摩擦以致损坏线圈结构、保证线圈处于较强的磁轨磁场中,本研究将气隙高度设置为5 mm,单匝线圈电流值为20 A,线圈匝数为125 匝,两个线圈电流方向相反。除此之外,为减小端部效应的影响,设置永磁轨道长度大于线圈长度,动子线圈结构始终位于永磁轨道中心位置。
5.1.3 仿真数据与实验数据对比
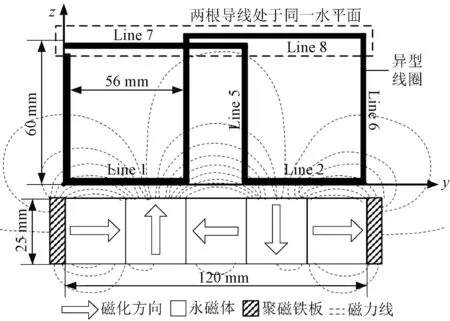
图8 磁轨磁场扫描坐标系Fig.8 Coordinate system of magnetic field of PMT
以1 mm为步长,使用磁场扫描仪扫描原Halbach磁轨沿导线路径的磁场分量。另一方面,仿真输出各导线在该路径处的磁场分量。通过实验与仿真得到的8段导线处的磁场分量对比结果,如图9所示。
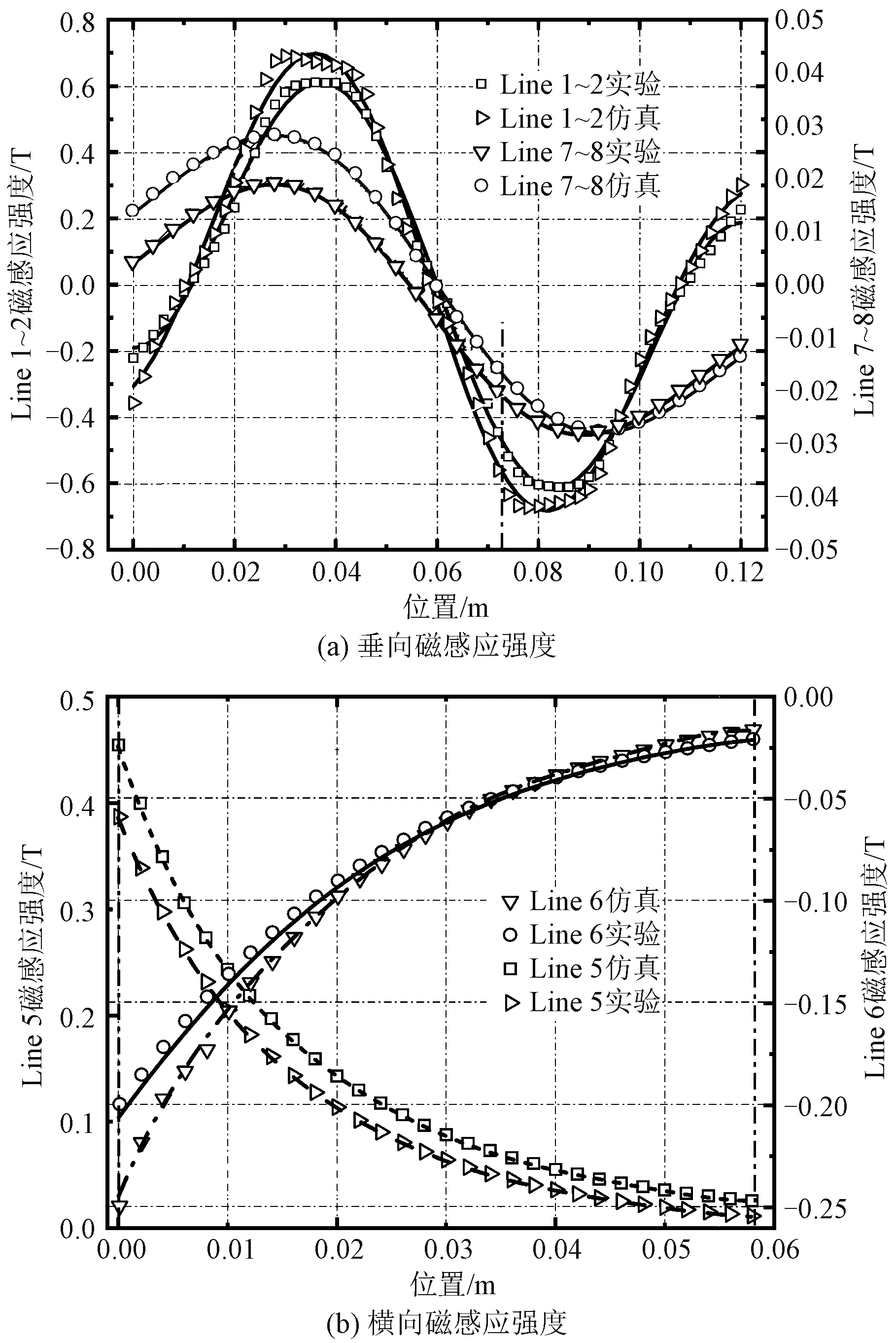
图9 (无铁心系统)各段导线磁感应强度的仿真与实验对比图Fig.9 Comparison of simulation and experimental results of magnetic induction intensity of each section of each conductor(system without iron)
5.1.4 误差分析
为衡量仿真模型的准确性,综合绝对误差、均方根误差和协方差定量分析模型误差。
绝对误差反映测量值偏离真值的大小。本文使用的永磁轨道为Halbach结构,磁场对称分布且磁轨两侧能够产生等值反向的垂向磁场,当利用仿真数据与实验数据的绝对误差表示两种方法计算磁感应强度分量的差异时,绝对误差可表示为:
Δ=|As-Atest|
(9)
式中,As、Atest分别为仿真、实验数据。通过分析磁轨两侧垂向磁场的相对误差,可得出两侧磁感应强度分量的差异,误差曲线如图10所示。Line 1~2、Line 7~8、Line 5、Line 6处磁感应强度的绝对误差较小,均在允许的误差范围内。
由于存储环境不当等原因造成永磁轨道磁场强度衰减以及实验过程中对Line 1~2扫描数据时的测量误差,使得实验测量到的磁轨左右两侧磁场强度不等,从而导致绝对误差曲线一侧产生峰值的突增(如图10(a)圆圈区域所示),但整体上绝对误差在允许范围内。
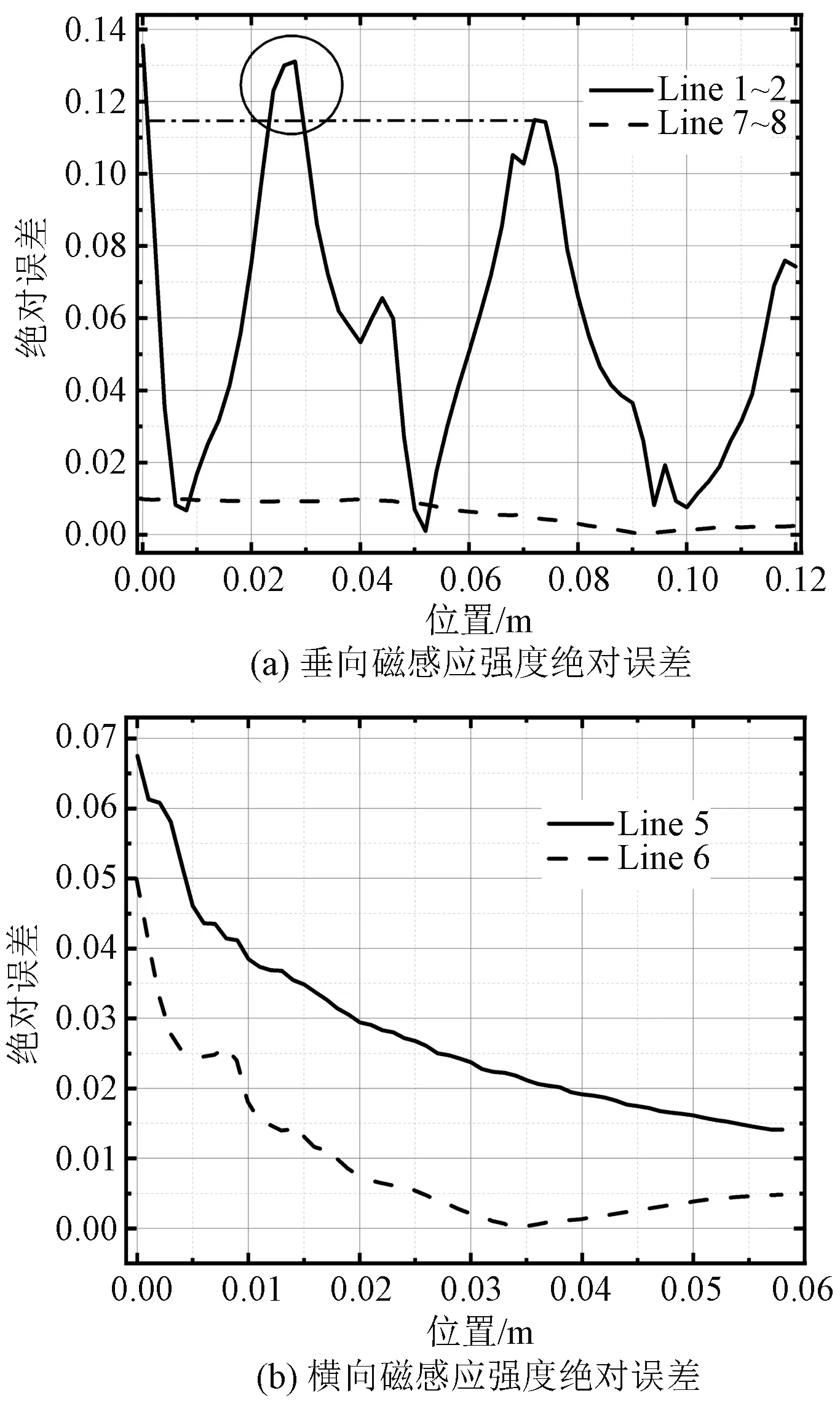
图10 各段导线磁感应强度的绝对误差对比图Fig.10 Absolute error contrast diagram of magnetic induction intensity of each conductor
均方根误差(Root Mean Square Error,RMSE)对一组测量中的特大或特小误差非常敏感,因此,计算仿真与实验数据之间的均方根误差用以反映出精密度。基于异形线圈的八根导线路径,当计算各导线磁感应强度仿真数据与实验数据的均方根误差时,可表示为:
(10)
式中,m为仿真/实验数据的个数。实验测量与仿真模型采用相同的磁轨,理想情况下二者数据完全相关,但数据受到测量、仿真误差等的影响,并不能做到完全一致,因此计算协方差(COVariance,COV)衡量实验与仿真数据的相关程度。表1提供了仿真与实验数据的均方根误差和协方差。

表1 仿真与实验数据的均方根误差和协方差Tab.1 Root mean square error and covariance of simulation and experimental data
由表1可知,Line 1~2、Line 7~8、Line 5、Line 6处磁感应强度的协方差均接近于1,因此说明仿真数据与实验数据相关程度较高;且均方根误差较小。
综合上述针对绝对误差、均方根误差和协方差的分析,可知仿真模型能够很好地模拟实际磁感应强度横向、垂向分量,可用于本文的仿真研究。
5.2 驱动力计算
基于前述无铁心非接触式驱动结构的三维静磁场模型,添加铁磁片实体模型,按照图9所示的导线路径,在ANSYS Maxwell有限元软件中仿真输出基于新型永磁轨道的非接触驱动系统(含铁磁片)磁感应强度横向、垂向分量,如图11所示。
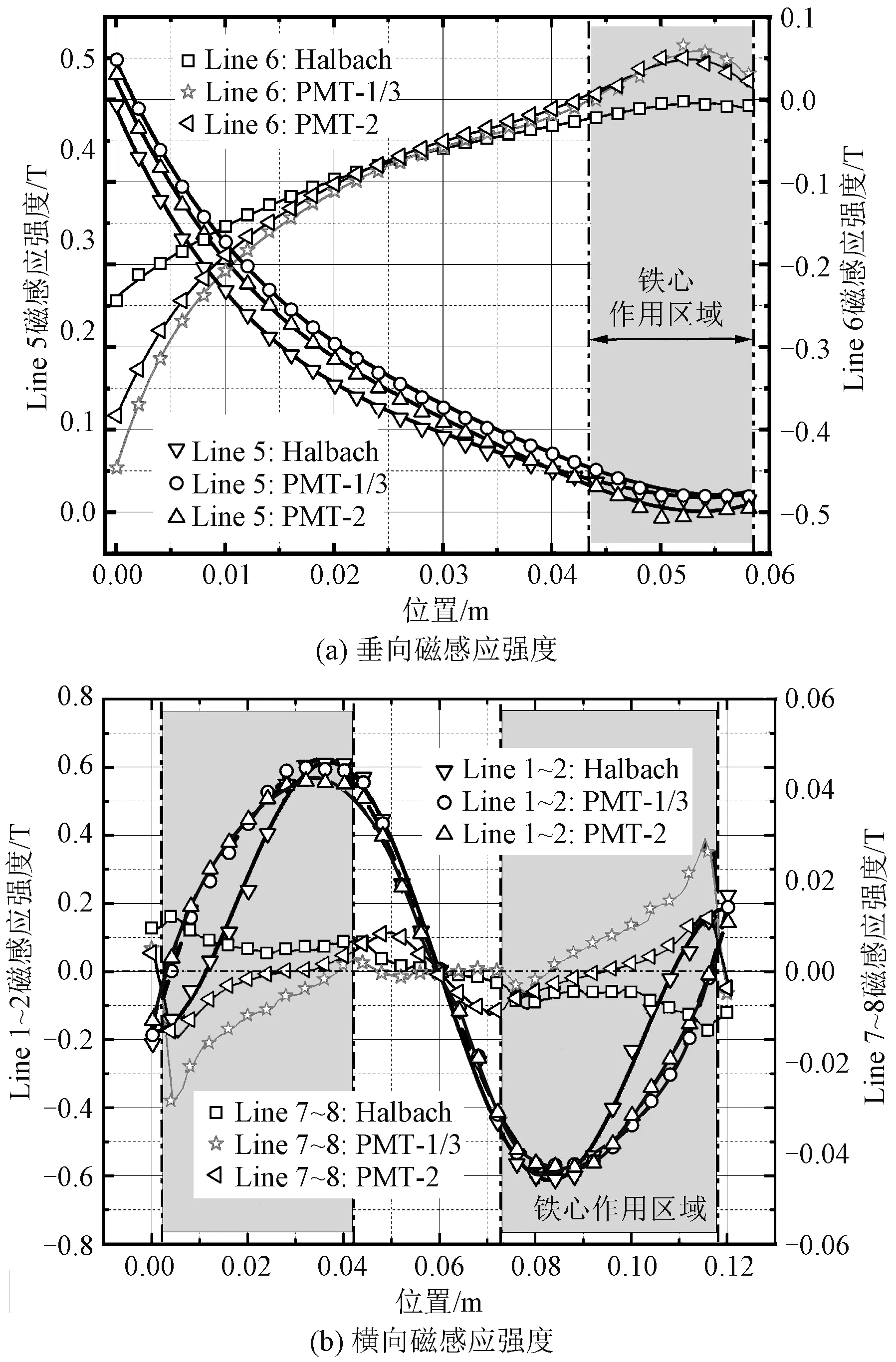
图11 (铁心系统)各段导线磁感应强度拟合结果图Fig.11 Fitting results of magnetic induction intensity of each conductor(system with iron)
图11(a)、图11(b)深色区域横向、垂向磁感应强度分量在铁磁片的作用下发生波动,这提供了产生纵向驱动力的磁场条件。
为进一步定量分析铁磁片对驱动力的影响,通过拟合法得出磁感应强度的表征式。由图11可知,磁感应强度-位置曲线近似正弦函数,符合周期性曲线变化趋势,因此利用傅里叶级数拟合法来拟合磁感应强度曲线[22,23]。图9异型线圈结构包括八条导线,采用傅里叶级数拟合法拟合八条导线处的磁感应强度分量时,傅里叶级数展开式为:
(11)
式中,i=1,2,…,8;Bi为第i段导线处的磁感应强度;p为拟合阶数;ai0、aip和bip为傅里叶系数;ωi为磁感应强度曲线拟合时对应的角频率;j为选定的展开阶数。拟合曲线如图11实线所示。将式(11)代入式(3),得出各新型磁轨磁场下异型线圈的驱动力见表2。
由表2可知,无铁磁片的非接触驱动系统驱动力近乎为0;由于有铁磁片的非接触驱动系统纵向存在波动磁场,因此单层线圈能够产生驱动力,基于三种新型磁轨的超导磁浮系统能够产生优于原Halbach的推力值。因此,新型永磁轨道达到了提高驱动力的要求,同时也证明了在异形线圈附近合理设置铁磁调控件能够产生理想的驱动力。

表2 (铁心系统)单匝导线的驱动力Tab.2 Driving force of single coil(system with iron)
6 结论
(1)针对高温超导磁浮系统悬浮、导向与驱动性能的要求,提出三种能够产生对称磁场的永磁轨道排列方式。
(2)对非接触式驱动方式进行了理论分析,建立了基于Halbach永磁轨道的非接触式无铁心驱动系统仿真模型,并与磁场扫描平台的实测数据对比,结果表明:缩减模型的仿真输出数据与实测数据基本重合,从而验证仿真模型的准确性。最后通过误差分析,得出仿真模型模拟精度可达99%以上,进一步验证了模型的准确性。
(3)基于非接触式无铁心驱动系统仿真模型,添加铁磁片实体模型,建立非接触式含铁心驱动系统仿真模型,利用傅里叶级数拟合方法拟合模型的仿真输出数据,得出基于新型磁轨的超导磁浮系统的驱动力,结果表明:在产生良好悬浮、导向性能的同时,能够产生较优的驱动力。除此之外,进一步验证了非接触式驱动方式理论模型的正确性。

