基于时序区间值模糊软集的电能质量综合评价

董海艳，田 宇，陈 杰，王运韬，赵炳文

(电力电子节能与传动控制河北省重点实验室(燕山大学)，河北 秦皇岛 066004)

1 引言

分布式电源的大规模渗透以及电力电子化设备、冲击性负荷、非线性负荷、波动性负荷的大量使用，使现代电网电能质量状况日趋复杂，污染排放更加严重，污染在时空分布的不确定性增强[1]。另一方面，电源、负荷设备的电力电子化和精密数字化特征日趋明显，对电能质量更加敏感，由电能质量问题造成的后果更加严重[2,3]。电能质量已经成为供用电双方普遍关注的问题。科学、全面评价电网电能质量对改善电网环境，提高电能质量运行管理水平具有重要意义，是电能商品“按质定价”以及污染损失量化的前提和基础。

电能质量是具有时空特性的多指标综合体。目前，关于电能质量评价的研究主要集中在单测点评价层面，从指标权重设置方法和评价方法两方面进行有益探索，根据某时间断面监测数据进行综合评估。常用评价方法主要包括模糊数学、灰色关联理论、可拓学、雷达图法、神经网络以及人工智能等方法[4-11]。考虑到单测点综合评价不能体现整个区域的电能质量状况，刘颖英、吴杰等人开展了区域电能质量评估研究[12,13]，综合多个节点的监测结果对整个地区电能质量状况进行综合评价。文献[14]采用“突出自身优势，弱化对手优势”的竞争原则，提出一种基于自主式决策思想的区域电能质量综合评估思想，旨在实现同一区域、相同时段、不同评估对象之间的比较。电能质量不仅具有区域空间特性，还具有动态时序变化特性。在单测点单个时间断面评价的基础上，文献[15]提出了一种基于激励惩罚机制的区域电网电能质量综合评价方法，能够突出各测点不同时段电能质量的动态差异性以及电能质量改善情况，能够结合多个时段的指标数据进行综合评价，极大改善了单个时间断面评价的片面性，但在评价过程中通过95%概率大值法取用监测数据，难以表征各时段内部电能质量的波动性。

通过上述分析可知，目前电能质量评估已逐渐由单个时间断面的评估转向多时段的综合评估，并在评价中突出体现电能质量的时序性特征。但样本数据的选取仍具有局限性，一般采用最大值法或95%概率大值法取用监测时段内某个时刻的数据。这种采用单个时刻的指标数据进行评估的方法无法体现电能质量扰动的波动性与不确定性，不能全面表征待评地区的电能质量状况。为此，本文提出基于时序区间值模糊软集的电能质量综合评价方法。考虑电能质量扰动的波动性特点，将评价周期内各时段的监测数据表示成区间值形式，构建时序区间值模糊软集；考虑电能质量扰动的时序性特点，将评价周期按照季节和时段进行横纵向分割，通过指标加权和纵横向时序集成，实现地区电能质量的多维度综合评价。算例结果表明，本文所提方法能有效避免单一数据评价方式的片面性，并能计及扰动的波动性和时序性从不同时间维度对各测点电能质量进行评价，且评价结果全面、具体。

2 时序区间值模糊软集概述

软集是由俄罗斯学者Mododtsov[16]于1999年提出的一套理论，软集理论是一种有效处理不确定问题的数学工具，近年来得到了不断完善与发展，已在决策问题和评价问题中得到了广泛应用[17-19]。软集以参数形式从多个角度对研究对象进行表征，本文将描述电能质量特征的指标作为参数，采用软集理论解决电能质量评价问题。软集的定义如下：

定义1[16]：设U为初始论域，P(U)为U的幂集，A为非空参数集，若F:A→P(U)为一个映射，则称(F,A)为论域U上的软集。

2001年，Maji等人将模糊集理论融入软集范畴[20]，通过参数隶属度描述研究对象的不确定性，确立了模糊软集概念，推动了模糊集与软集的融合发展，陆续出现了区间值模糊软集、直觉模糊软集等一系列研究成果。

定义2[20]：设U为初始论域，A为非空参数集，M(U)为所有模糊软集的全体，若F:A→M(U)为一个参数集A到M(U)的映射，∀e∈A,F(e)={〈x,μF(e)(x)〉:x∈U}∈M(U),μF(e)(x)为元素x属于模糊集F(e)的隶属度，则称(F,A)为论域U上的模糊软集。

定义3[21]：设U为初始论域，ψ(U)为所有区间值模糊软集的全体，A为非空参数集，若F:A→ψ(U)为一个映射，则称(F,A)为集合U上的区间值模糊软集。

考虑到研究对象的属性参数信息可能随时间变化，体现一定的动态时序性特征，将区间值模糊软集与时序模糊软集[22]相结合，构成时序区间值模糊软集，综合多个时刻的信息描述研究对象，然后进行决策或评价。

定义4：设U为初始论域，A为非空参数集，T为时间集，ζ(U)为所有时序区间值模糊软集的全体，若F:A×T→ζ(U)为一个参数集到ζ(U)的映射，则称(F,A×T)为集合U上的时序区间值模糊软集。

3 评价算法设计

本文采用时序区间值模糊软集对区域电能质量进行综合评价，算法流程如下：①构建电能质量综合评价指标体系，并对各指标区间值数据进行模糊处理；②确定指标权重与时序性权重；③构建电能质量评价问题的时序区间值模糊软集；④根据指标权重和时序性权重进行指标加权和纵横向时序集成处理，构建评价矩阵；⑤定量计算待评区域各测点的评价值，得到综合评价结果。

3.1 指标选取与模糊处理

本文针对稳态电能质量问题进行分析，选取的评价指标包括三相不平衡度(X1)、电压波动(X2)、谐波畸变(X3)、电压闪变(X4)和电压偏差(X5)。指标类型与数目可根据地区负荷的需求适当调整。

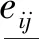
本文采用半梯形隶属度函数对各项指标进行模糊处理。由于选取的各项评价指标均属于极小型指标，所以各指标区间值数据统一采用式(1)和式(2)所示函数进行处理。

(1)

(2)

3.2 时序性权重和指标权重确定

3.2.1 时序性权重确定方法

考虑到新能源出力和负荷用电具有周期性、季节性等时序性特点，本文将一年的评价周期按季节和时段进行纵横向分割，从不同维度对电能质量进行评价研究。纵向划分为p季，每季12/p个月，各季再横向划分为q个时段，一天中的一个时段含24/q个小时。本文不区分各季以及各时段数据信息在评价中的重要程度，各季的时序性权重如式(3)所示，各时段的时序性权重如式(4)所示。

(3)

(4)

3.2.2 指标权重确定方法

本文采用G1法和熵权法相结合的组合赋权法对评价指标赋权。其中G1法是一种主观赋权方法，相比于层次分析法，不需要进行一致性检验，简单、直观、计算量小。由G1法得到的权重向量为wG=[wG1,wG2,…,wGn]T。熵权法通过熵表示事物的不确定性，是一种将信息量和指标权重关联起来的客观评价方法。由于不同季、不同时段的电能质量状况具有差异性，因此有必要根据各自的指标信息量确定相应的权重。将一年评价周期进行纵横向分割后，每季每个时段共含8 640/(pq)个小时的监测数据，根据各指标数据确定权重的方法如下：

(1) 根据各测点的指标监测数据获取指标区间值数据，构建区间监测值矩阵E：

(5)

(2) 采用min-max标准化方法，对区间监测值矩阵中的数据进行线性变换，构建标准区间监测值矩阵E*:

(6)

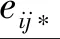
(7)

(8)

(9)

(10)

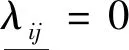
(11)

(12)

(6) 根据区间变异程度系数向量计算区间熵权重向量wS，其第j个元素wSj如式(13)所示：

(13)

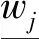
(14)

(15)

由wGj和wSj根据式(16)计算评价指标的综合权重：

(16)

3.3 构建时序区间值模糊软集

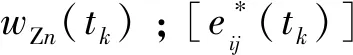
表1 软集(F,A×T)的信息表Tab.1 Table of a soft set of (F,A×T)

3.4 构建评价矩阵

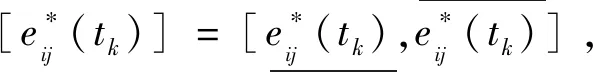
(17)

(18)

(19)

(20)

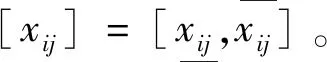
(21)

(22)

构建评价矩阵S，如式(23)所示：

(23)

采用上述纵横向时序集成方式可实现整个评价期内各测点电能质量的综合评价，若预对比不同季或不同时段的电能质量情况，可采取仅横向时序集成、仅纵向时序集成或无时序集成的方式解决。

3.5 评价值的定量计算

根据评价矩阵，生成各待评测点ai的评价区间，如式(24)所示:

(24)

由评价区间可得各测点的电能质量综合评价结果ci为：

(25)

4 算例分析

4.1 基础数据

本文对某“光伏+电采暖”试点区域6个测点在2020年的电能质量情况进行综合评价。居民安装的屋顶光伏容量包括3 kW、4 kW和5 kW三种不同规模，电采暖有直热和蓄热式两种类型。模糊化参数见表2。

表2 指标模糊化参数Tab.2 Table of index fuzzy parameters

在算例中，纵横向分割参数p和q均取为4，因此，各季以及各时段的时序性权重均为0.25。

结合专家意见，给出G1法评价指标的排序结果，X5>X3>X4>X2>X1；指标X5与指标X3相对重要程度之比r2=1.3，指标X3与指标X4相对重要程度之比r3=1.2，指标X4与指标X2相对重要程度之比r4=1.2，指标X2与指标X1相对重要程度之比r5=1.0；由G1法得到的各指标权重分别为0.154、0.154、0.221、0.184和0.287。

根据式(5)～式(15)求取各季各时段的区间熵权重，结合G1法权重根据式(16)计算评价指标的综合权重见表3。由表3可知，不同时段的指标权重具有一定的差异性，但各指标所占权重的总体趋势具有相似性，电压偏差指标权重最大，在0.4左右，而其余4个指标基本在0.1～0.2范围内变化。其中，这些权重的差异性充分体现了不同时段各指标之间变化规律、幅度或趋势具有差异性；而这些权重的相似性充分体现了电压偏差扰动在不同时段的各测点之间均具有较大变化，是该地区电能质量评价中占主导作用的关键指标。表3中，Tij为第i季第j个时段。

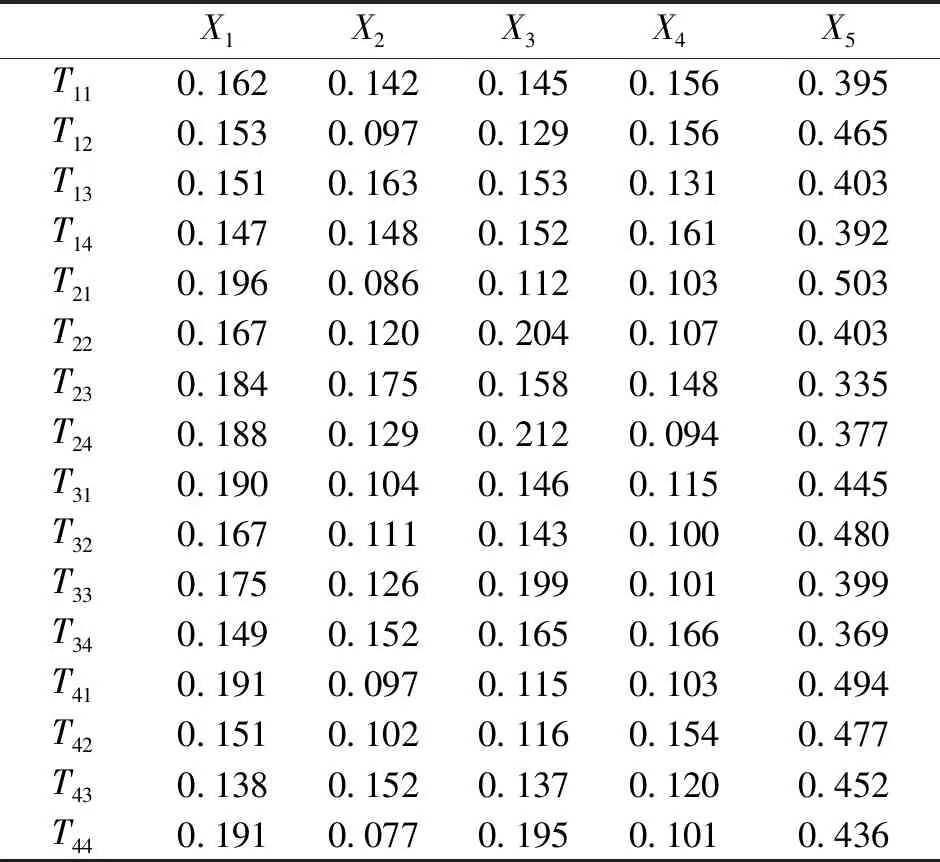
表3 指标性权重Tab.3 Table of indicative weight

4.2 不同时序集成方式的对比分析

本文通过对比不同时序集成方式，对同一供电范围不同测点的电能质量进行区域横向比较，对同一测点不同季或不同时段的电能质量进行时域纵向比较。

4.2.1 无时序集成方式

图1给出了不进行横纵向时序集成方式下待评测点各时段的评价结果。

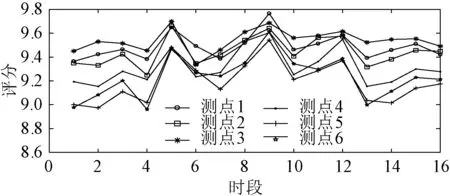
图1 无时序集成方式的评价结果Fig.1 Evaluation results of time-free integration

图1反映了：①第2季的1时段、4时段以及第3季的1时段、4时段各测点的评价值相对较高，而第1季和第4季各时段的评价值变化相差不大，且普遍偏低；②各测点16个时段评价值的变化趋势具有较强的一致性。原因主要有2个方面：一是受光伏出力影响，各季的2时段、3时段电压偏差污染严重，评价值较低；二是受电采暖负荷影响，第1季和第4季的1时段、4时段电压偏差和三相不平衡污染严重，评价值也较低。该评价结果真实反馈了新能源以及波动性负荷接入对该地区电能质量的影响，充分验证了本文所提方法能够准确表征电能质量的时序性特征，验证了模糊软集评价的可行性及有效性。

无时序集成方式能够给出各季各时段的电能质量评价结果，可实现每个测点各时序的纵向对比，便于查找评价值较低时段的污染原因；可实现各个测点在不同时序的横向对比，便于分析污染的空间分布情况。

4.2.2 横向时序集成方式

图2为横向时序集成方式的评价结果。通过对比4个季度的评价值可知，多数测点在第1季和第4季评价值较低，具有明显的季节性特征。可见，在第1季和第4季，光伏和电采暖负荷的叠加作用加深了污染的严重性。从评价结果可清晰看出，采用横向时序集成方式有助于分析具有季节特性的污染源对测点电能质量的影响。对各测点的电能质量水平进行横向对比可知，测点3在各时段的评价值均高于其他测点，测点2次之，测点5在各时段的评价值最低。

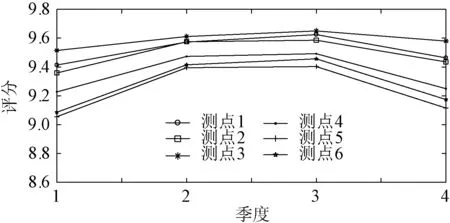
图2 横向时序集成方式的评价结果Fig.2 Evaluation results of horizontal sequential integration

4.2.3 纵向时序集成方式

图3为纵向时序集成方式的评价结果。通过对比4个时段的电能质量状况可知，各测点在第2时段评价值最低，第3时段的评价值稍次于第4时段，第1时段的评价值最高，在一天内具有明显的时序性特征。可见，光伏对各测点电能质量的影响较大，同时采暖期内蓄热式电采暖负荷在第4时段对电能质量的影响显著高于第1时段。显然，采用纵向时序集成方式有助于分析在一天内具有时序性特征的各测点电能质量状况。

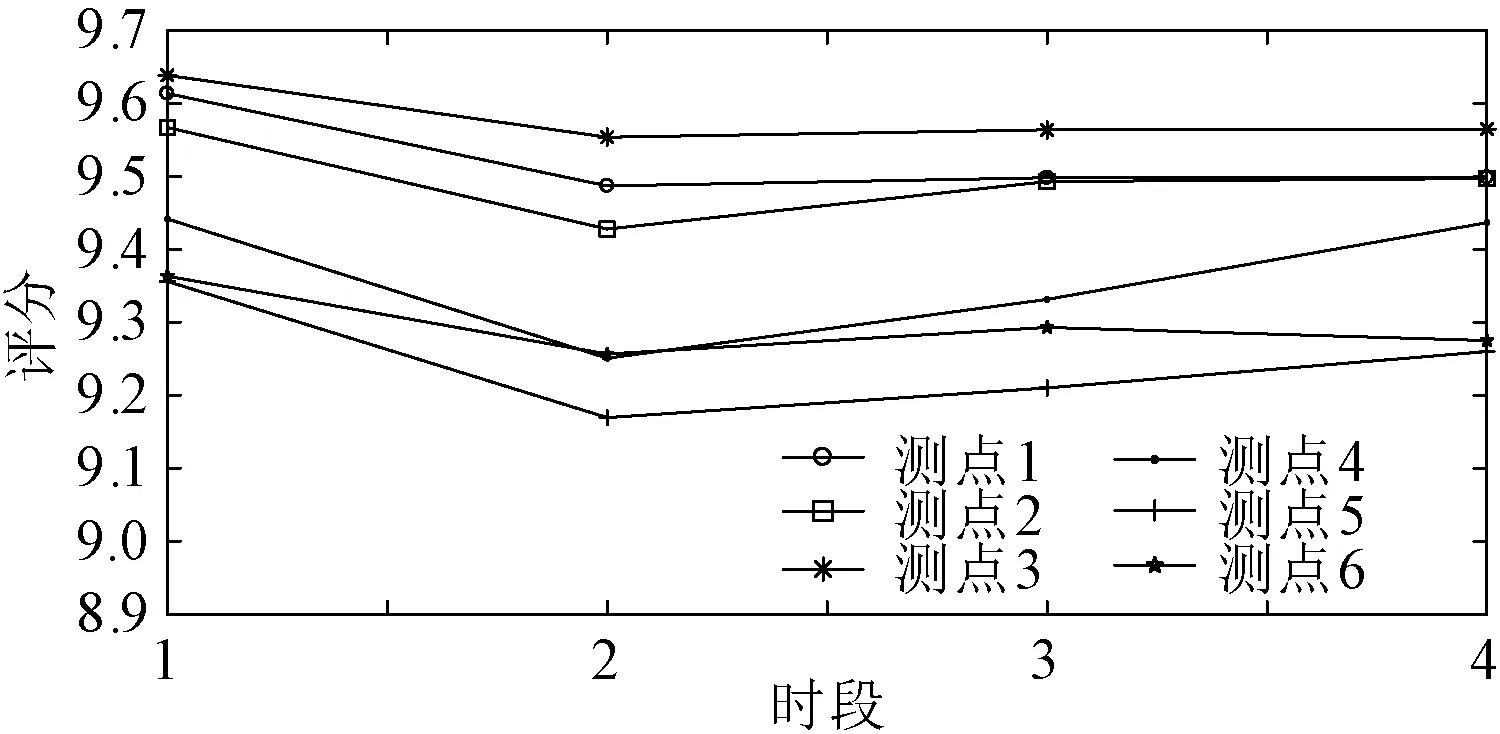
图3 纵向时序集成方式的评价结果Fig.3 Evaluation results of vertical time series integration

4.2.4 纵横向时序集成方式

采用纵横向集成方式对各测点进行电能质量评价的结果分别为9.553、9.533、9.620、9.401、9.290、9.338，电能质量由优到劣依次为测点3、测点1、测点2、测点4、测点6和测点5。对比各测点的空间分布可知，电能质量较差的测点距离电源相对较远。

将无时序集成、纵向时序集成和横向时序集成方式中各季各时段的评价值相加，可得到各测点整个评价周期内的综合评价值。通过对比无时序集成、纵向时序集成、横向时序集成和纵横向时序集成方式可知，4种方式的综合评价结果排序完全相同，即采用4种集成方式对各测点整个评价周期内的电能质量状况进行综合评价，其结果是完全一致的。若需对比每个季每个时段的评价结果，采用无时序集成方式；若需对比各个季的评价结果，采用横向时序集成方式；若需对比各个时段的评价结果，采用纵向时序集成方式；若仅需对比整个评价周期的综合评价结果，任意一种集成方式均可。

本文在3.2节设置的时序性权重是相同的，各时段或各季节的电能质量数据在评价过程中具有相同的作用，若需要对不同时段或季节的电能质量状况有所侧重，可通过时序性权重进行调节，此时若需对比整个评价周期的综合评价结果，则需采用纵横向时序集成方式。

4.3 不同波动范围的对比分析

为分析验证不同波动范围对评价的影响，采取扩大和缩小测点2各指标在各时段的区间监测值范围的方式，新增3个测点。保持E2=[[e21],[e22],…,[e2n]]内各指标的区间下限值不变，增大区间上限值，形成测点7的区间监测值；保持E2内各指标的区间下限值不变，减小区间上限值，形成测点8的区间监测值；保持E2内各指标监测数据的区间长度不变，同时增大上、下限值，形成测点9的区间监测值。采取4种集成方式对9个测点在整个评价周期的电能质量进行综合评价的结果见表4。

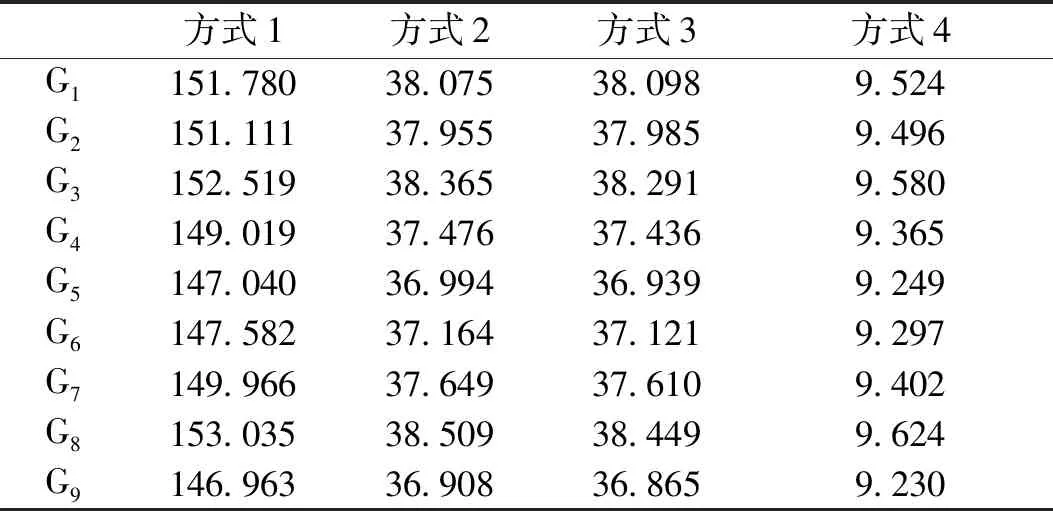
表4 综合评价结果Tab.4 Table of comprehensive evaluation results

通过对比可知，4种方式下9个测点的评价值排序结果一致，充分验证了本文采用4种集成方式进行各测点电能质量进行评价的可行性。此外，与4.2节未增加3个测点时的排序进行对比可知，增加测点并不会改变原有各测点之间的排序情况。

对测点2、测点7、测点8和测点9的电能质量情况进行分析可知：测点2和测点7进行对比，因测点7增大了测点2的区间上限值，电能质量污染更加严重，波动区间更大，所以测点7的评价值低于测点2；测点2和测点8进行对比，因测点8减小了测点2的区间上限值，电能质量污染减轻，波动区间减小，所以测点8的评价值高于测点2；测点7和测点9进行对比，两者的区间上限值相同，测点9的区间下限值高于测点7的区间下限值，显然测点7的电能质量优于测点9，所以测点7的评价值高于测点9；测点2和测点9进行对比，两者波动区间相同，但测点9的区间上下限都高于测点2，所以测点2的评价值高于测点9。表4结果充分验证了本文方法的有效性，也充分表明采用区间值形式进行电能质量评价相比单一监测值评价更具合理性。

4.4 不同评价方法的对比分析

为分析验证本文方法相比其他电能质量综合评价方法的有效性，将本文时序区间值模糊软集的评价方法与加权秩和比 (Rank Sun Ration,RSR)算法、理想解算法进行了对比分析。为增强与本文方法的可比性，将加权RSR算法和理想解算法的指标权重与本文的指标权重设置成相同的权重值，并将加权RSR算法和理想解算法的评价周期分为3种类型，分别按照季度评价、时段评价以及一年的综合评价与本文方法进行对比。第一种将一年按季节分为4个评价周期，每个季节给出一个评价结果；第二种将一年按时段分为4个评价周期，每个时段给出一个评价结果；第三种将一年作为一个评价周期，给出一个评价结果。加权RSR算法和理想解算法根据95%概率大值在一个评价周期内取用监测数据。图4给出了评价周期为第一种类型时加权RSR算法和理想解算法的评价结果，通过与图2进行对比可知，3种方法4个季度的电能质量排序结果基本一致。对比按照另外两种类型划分评价周期时的评价结果可知，3种方法的电能质量排序结果也是一致的。上述对比充分验证了本文方法的有效性。

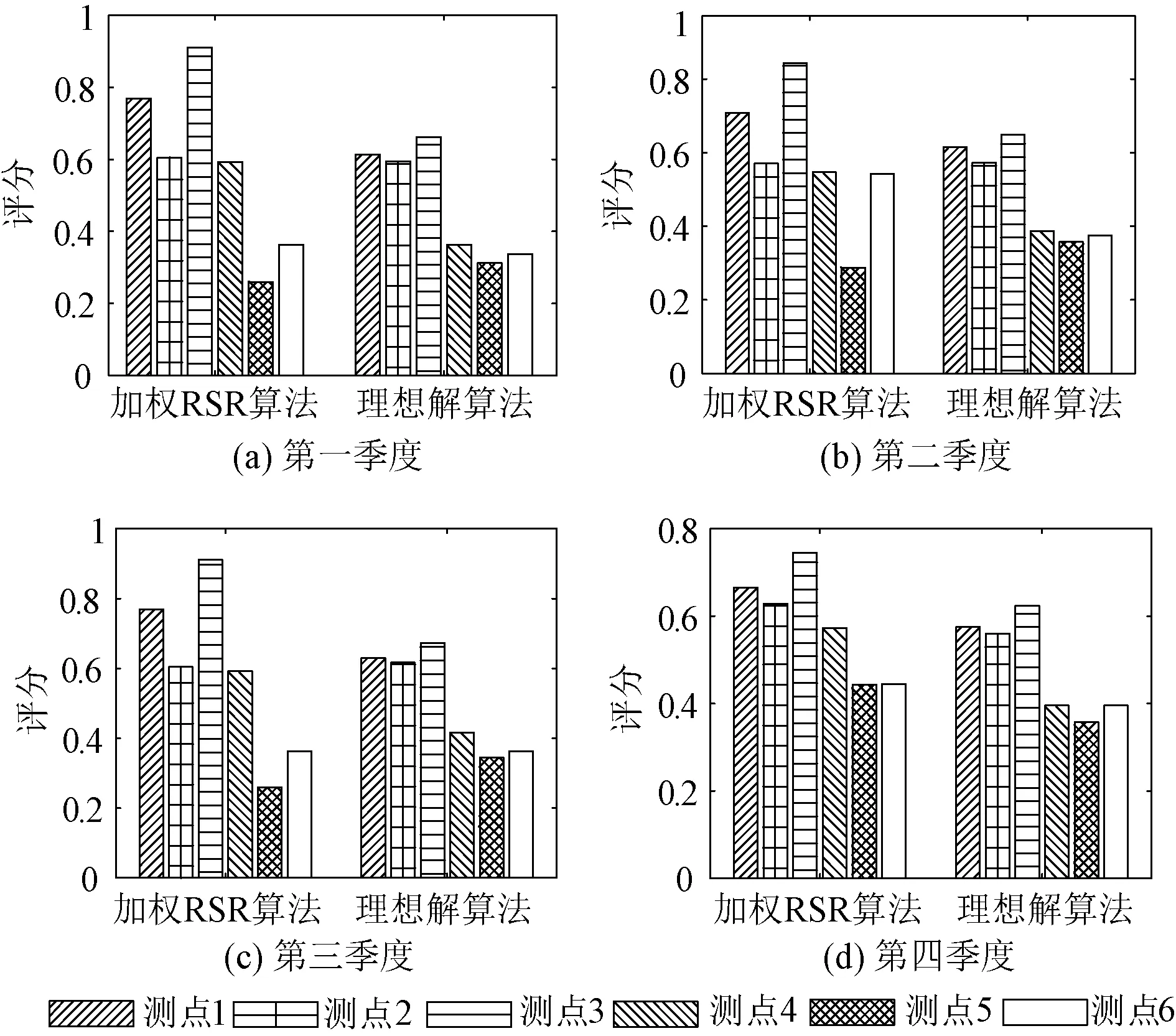
图4 不同方法的评价结果Fig.4 Evaluation results of different methods

此外，相比加权RSR算法、理想解算法以及其他评价方法，本文独具两大优势：一是本文方法通过不同集成方式，能够从不同维度展现电能质量扰动的时序性特征，并通过调节时序性权重，能够突出某些季节或时段在整个评价过程中的作用。而采用加权RSR算法和理想解算法等传统评价方法，即使对评价周期进行纵横向分割，也只能对各季或各时段分别进行评价，仅能得到一个个孤立的评价结果，不同季或不同时段之间不能进行比较，不能体现电能质量扰动的时序性特征。例如，图4中每个测点的4个季度之间无法进行对比，不能体现电能质量扰动的季节性特征；二是本文方法通过区间值方式，能够体现扰动的波动范围对电能质量的影响(例如4.3节算例)，评价结果更具合理性。而采用传统评价方法，只能通过监测时段内某个时刻的数据进行评价，无法体现电能质量扰动的波动特征，不能针对波动大小给出相应的评价结果。

5 结论

本文考虑电能质量污染的波动性和不确定性，提出了一种基于时序区间值模糊软集的电能质量综合评价方法。通过区间值方式表征电能扰动数据能够避免单一监测数据难以体现扰动波动范围的弊端，提高评价的合理性；采用横向、纵向、纵横向以及无时序集成方式能够从不同维度充分展现电能质量扰动的时序性特征，提高评价的全面性和具体性；本文所提基于时序区间值模糊软集的评价方法不仅适用于电能质量综合评价，同样适用于指标参数具有波动性、时序性、不确定性特征的其他对象评价，具有很强的拓展性。