大型轨梁粗轧BD1轧机主传动系统扭振特性研究

刘益民，王定勇，李 红

(1.鞍钢重型机械有限责任公司，辽宁 鞍山114031；2.攀钢钒轨梁厂，四川 攀枝花 617000；3.鞍钢重型机械设计研究院，辽宁 鞍山114031)

0 前言

主传动系统作为轨梁轧机传递运动和力矩的主要装置，轧制过程中会不可避免的发生扭振[1,2]。现场实践表明，在轧制某些典型产品时，易引起轨梁轧机主传动系统运行不稳，出现异常振动，影响产品质量和生产周期。

目前国内外学者对于轧机扭振特性主要从动力学建模和仿真模拟两大方面进行了广泛研究。在动力学模型方面，魏立新等[3]将电机转子偏心视为系统内扰研究轧机扭振系统，并采用神经网络速度控制器对系统进行控制。时培明等[4]分析了电机扰动力矩和轧制负载力矩共同作用下非线性扭振系统共振特性。张义方等[5,11]将电流谐波与轧制力谐波共同作用下的扭振系统进行研究，发现谐波激励与主传动系统扭振强弱变化的相关性。张瑞成等[6]应用自抗扰技术对轧机主传动系统扭振进行控制。高崇一等[7,8]对机电耦合机理及其影响因素进行研究，并将多间隙碰撞影响的轧机主传动扭振系统进行分析。刘彬等[9]针对咬钢突加负载时轧机主传动系统轴系的扭振现象，引入扭振减振器控制装置，建立电动机与扭振减振器的抑制模型。

在建模仿真方面，孙建亮等[10,11]研究了六辊轧机扭转振动与辊系动力学行为，通过建立的轧机扭振模型，分析某厂1100六棍轧机的扭振特性，当轧机持续扭振时，系统单位轧制力和前后张应力的分布情况会发生复杂的变化。之后计算了某热轧机水平振动和主传动系统的固有频率和主振型，然后对该轧机主传动系统和辊系振动情况进行综合测试，发现该轧机水平振动最剧烈，并引起轧机垂直振动和主传动系统扭振。苏旭涛等[13]针对易发生振动的F2轧机主传动系统建立动力学模型，并计算出主传动系统的固有频率和主振型。郭潇樯等[14]通过Ansys有限元软件定义耦振模型相关参数，根据图纸尺寸建立某轧机主传动系统及带材结构模型。并对所建模型进行模态分析，得出轧机主传动系统及带材结构模型的固有频率以及所对应的振型。朱小龙等[15]建立F2轧机主传动系统和轧机机架等零部件有限元模型，以节点耦合的方式模拟轧机内部各零部件之间的连接关系，进行有限元模态分析，计算结果与测试结果较为相符。

现有文献多采用单一的动力学模型和有限元法，且多是对单个零部件进行固有特性分析，忽略轧辊与接轴、万向节、主联轴器等部件之间的互相作用，且对重要部件简化成一体或省略，遗漏轧机局部模态影响，鲜有将两种方法融合建立轧机主传动系统整体模型的研究文献。本文基于某厂轨梁轧机，建立主传动系统整体模型，通过动力学模型与有限元对其扭振特性进行研究，为进一步研究轧机动态特性提供理论参考。

1 轨梁轧机主传动系统动力学建模

1.1 动力学建模

轨梁轧机主传动系统结构如图1所示，将主传动系统关键零部件等效为集中转动惯量和等效刚度，并建立两种形式主传动系统动力学模型，如图2所示，图2a考虑了主传动系统上、下分支的非对称结构特征，从减速机分速齿轮(J5/J6)处将系统分成两个分支，形成分支式系统；图2b主要考虑了轧机主传动系统整体特性，将两种并联系统进行简化，形成直串式动力学系统。J1-J12为各部件转动惯量，依次为电动机、主联轴器(电机侧)、主联轴器(减速机侧)、减速机高速齿轮、上低速齿轮、下低速齿轮(减速机侧)、上接轴头(减速机侧)、下接轴头(减速机侧)，上接轴头(轧辊侧)、下接轴头(轧辊侧)、上工作辊、下工作辊。K1～K11为各部件扭转刚度，依次为电动机轴、联轴器、输入轴、上输出轴、下输出轴、上接轴头、下接轴头、上接轴、下接轴、上工作辊、下工作辊。

图1 轧机主传动系统结构简图

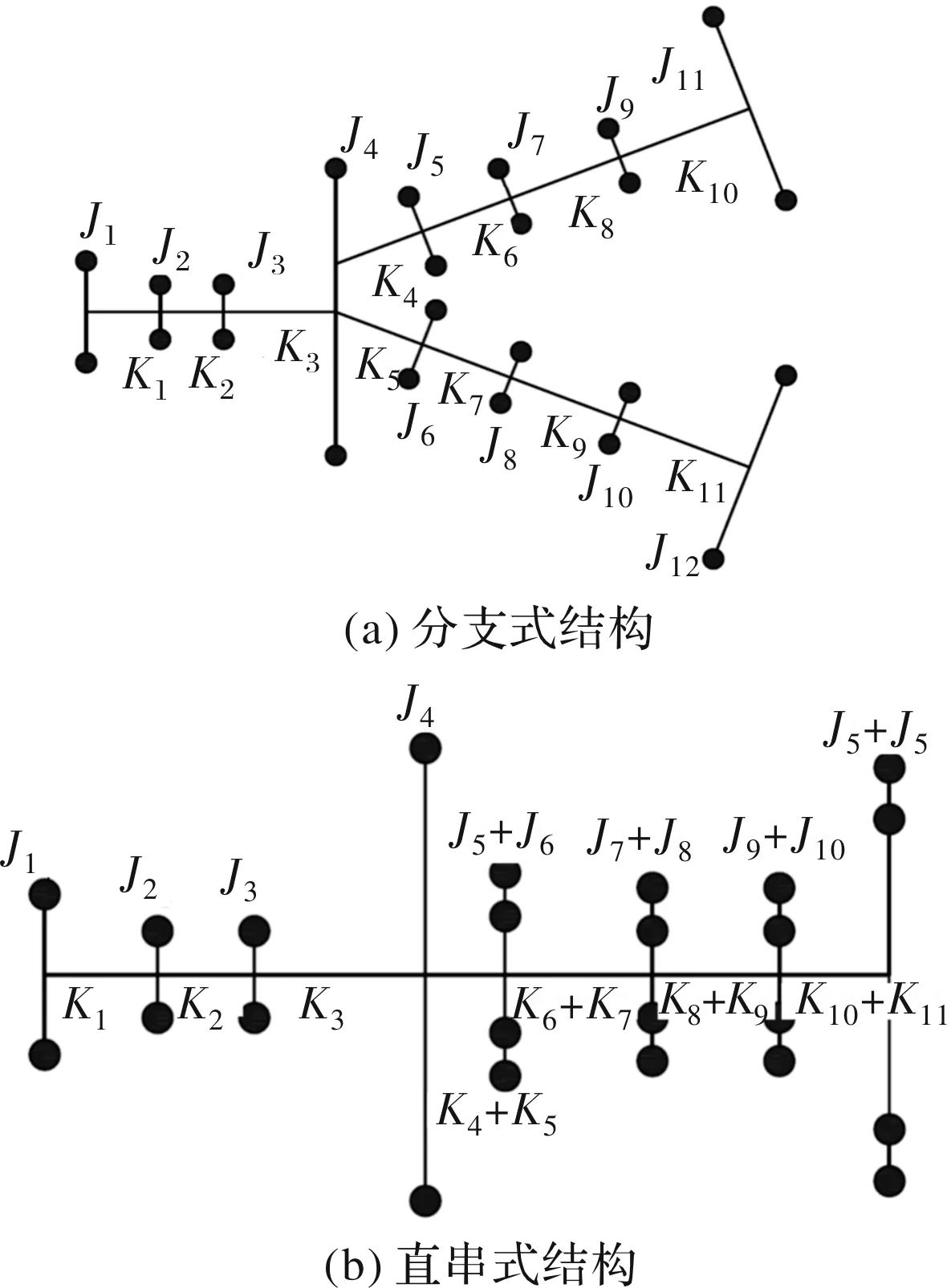
图2 传动系统简化模型

基于Lagrange函数和耗散函数建立系统动力学方程。假设模型各转动原件为J1,J2,J3…Jn，对应转角φ1,φ2,φ3…φn，建立轧机主传动系统扭振动力学模型。

(1)

式中，T为系统动能，U为系统势能，φi表示惯性原件转角向量，MFi为外扭矩。

无阻尼状态下轧机主传动系统扭振动力学模型

(2)

1.2 关键参数等效与转化

传动系统不同轴段在减速机前后存在转速差异，将改变其结构特性。为方便计算，将分支式系统等效为与主系统转速相同的系统，可通过合理等效转动惯量和转动刚度实现系统统一。以工作辊转速为基准，按照轧机主传动系统设计得到简化模型各部分转动惯量如表1所示。

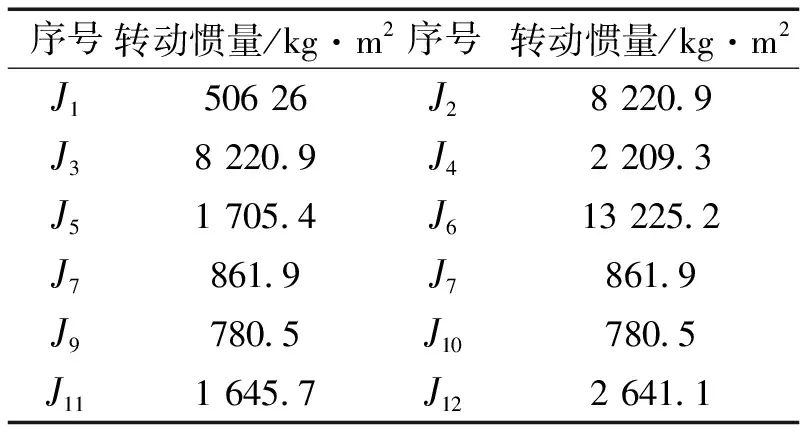
表1 轧机传动系统等效转动惯量

同理，以工作辊转速为基准，得到主传动系统简化模型各部分等效扭转刚度，如表2所示。

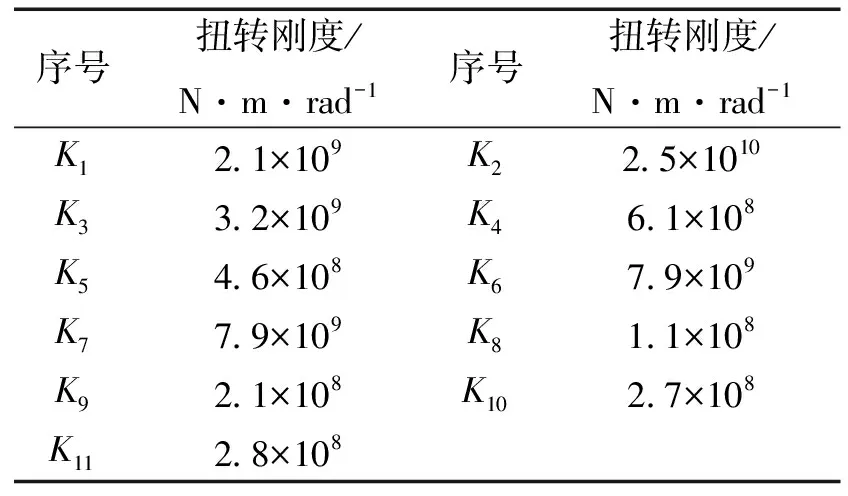
表2 轧机传动系统等效扭转刚度

2 轨梁轧机主传动系统有限元建模

轧机结构复杂，零部件众多，分析时倒角、螺栓及箱体类零件等局部特征对整体影响很小，且会严重影响计算资源，因此根据轧机设计图纸及相关简化原则，建立轨梁轧机主传动系统有限元简化模型如图3所示，包含电机转子、主联轴器、齿轮箱、十字万向接轴及轧辊等。

图3 主传动系统有限元简化模型

在模态分析前处理中，依据实际各零部件材料添加专属材料库，表3为主传动部分材料属性，其他零部件依据实际添加。如图4所示为主传动系统整体及部分局部网格划分，采用solid185单元，实体采用四面体划分方式，手动设置接轴、万向节等网格细节，整体网格单元433 544，节点792 476，精度保持在0.8以上。在主电机、齿轮箱、轧辊所有轴承支撑处添加Remote Displacement约束，即可绕Y轴线旋转，其他平动和旋转自由度约束，符合实际工况。

图4 主传动系统整体及局部网格

表3 主传动系统材料

3 结果分析与讨论

3.1 分支式系统计算结果分析

考虑上、下系统存在对称性，将上下分支分别表示为8阶振型。模态固有频率计算结果如表4所示。

表4 分支式系统固有频率

将分支式上、下系统对应振型分布绘制于同一图中。如图5与图6所示分别为第2阶与第3阶主振型，振型对称，均是由输出齿轮轴开始扭转幅值逐渐变大，工作辊扭振幅值最大，且与输出齿轮轴出现较大差值，易引起辊系传动系统扭振失稳。

对照组(不加药)在不同时间点对PC3细胞的凋亡作用差异无统计学意义(P>0.05)；雷公藤内脂醇的浓度为10、20、40 nmol/L时，培养PC3细胞12 h、24 h、48 h后对PC3细胞的凋亡作用差异有统计学意义(P<0.05)，见表2。

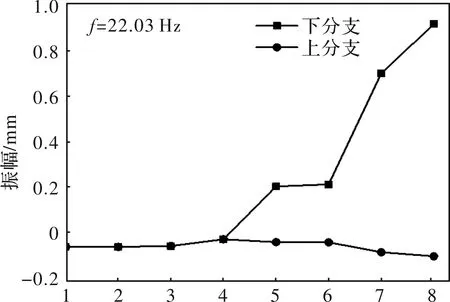
图5 第2阶主振型

图6 第3阶主振型

如图7和图8所示为第4阶和第5阶主振型，振型对称。在输出齿轮轴和接轴轴头位置发生反向扭转，而在扁头和工作辊位置发生较大正向扭振，二者通过接轴连接，此时接轴扭转差较大，受到较大扭转应力。

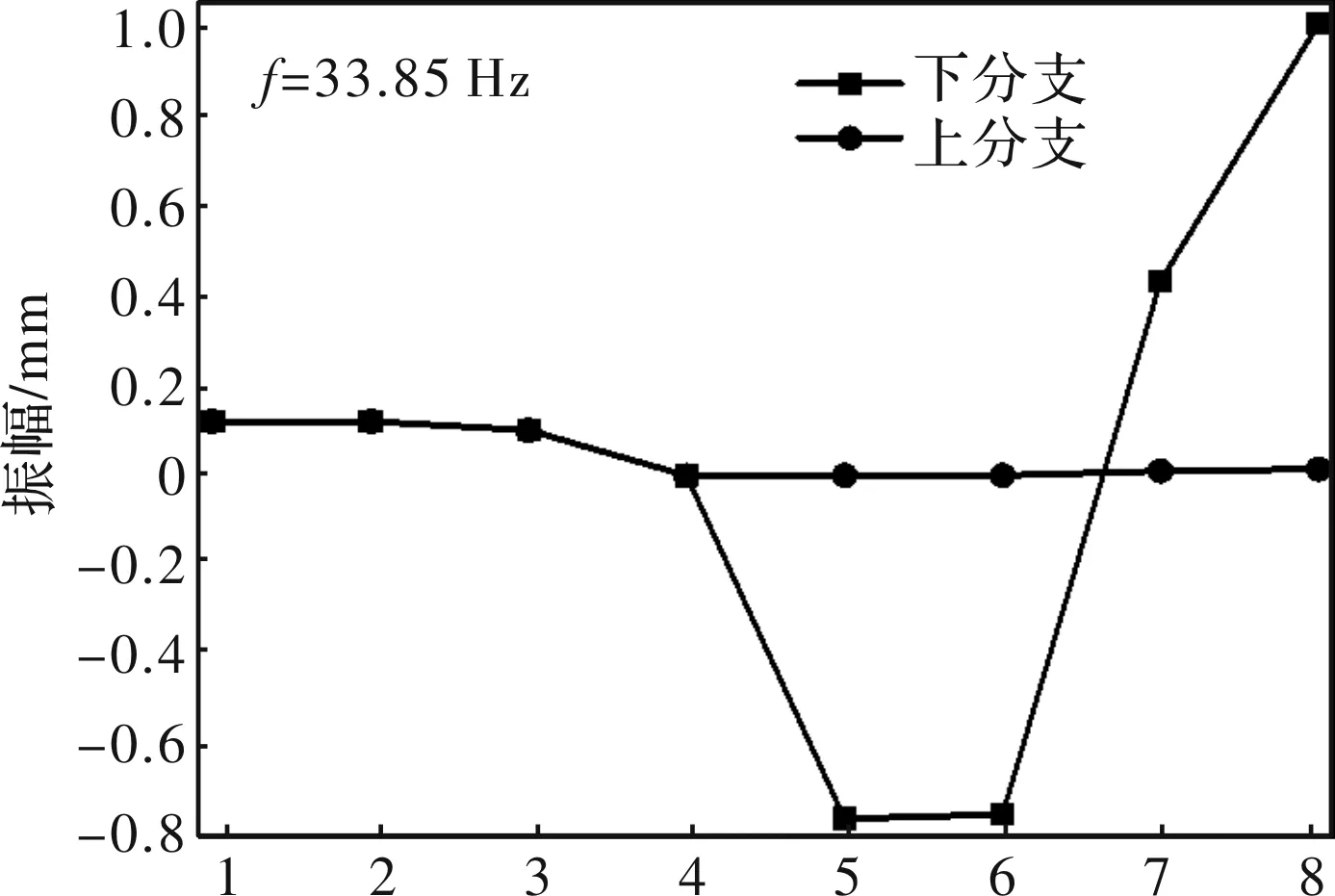
图7 第4阶主振型

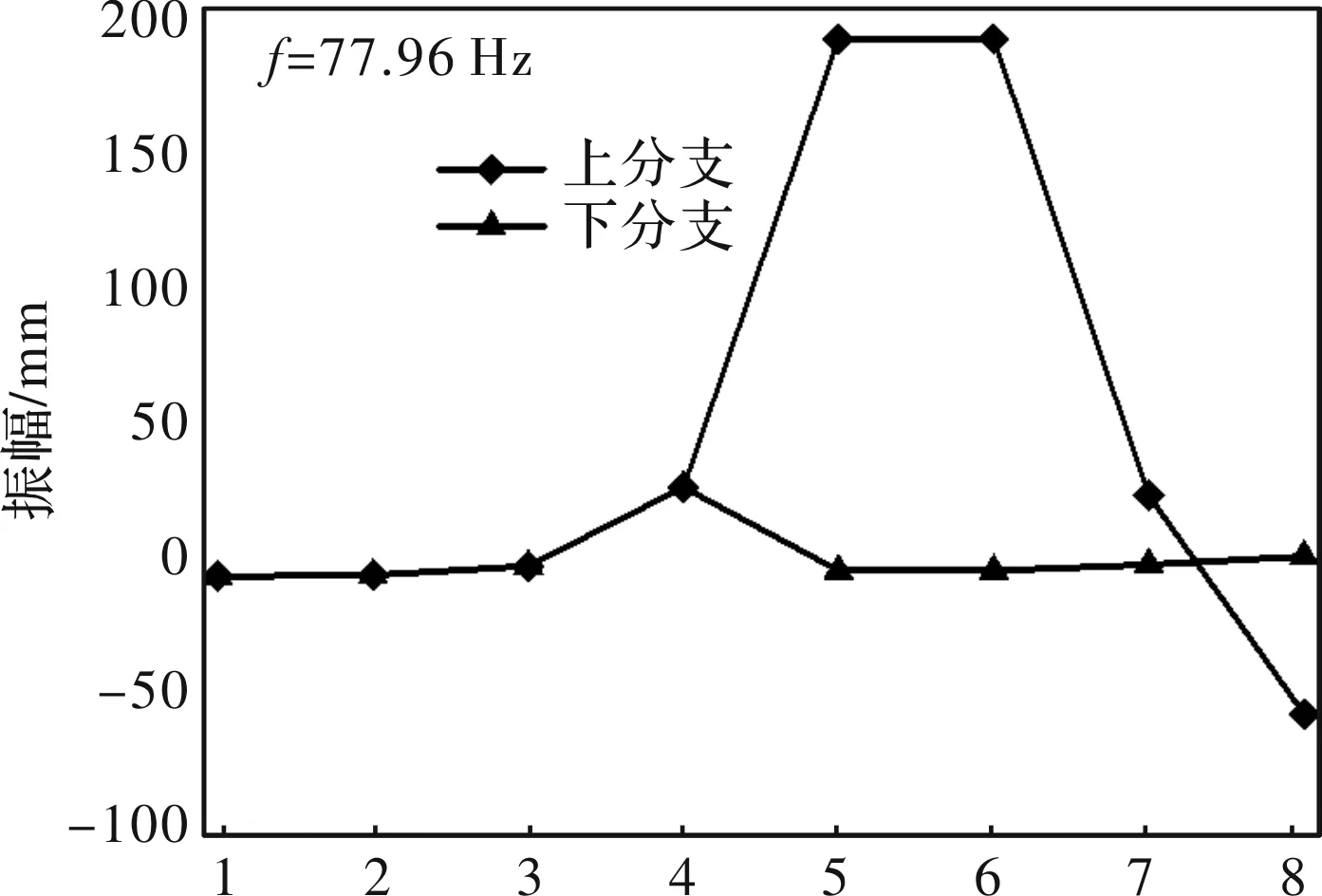
图8 第5阶主振型

如图9和图10所示为第6阶和第7阶主振型，表现出上下分支的对称特性。在此两种振型下，工作辊扁头和工作辊发生较大扭振，工作辊发生正向扭转现象。

图9 第6阶主振型

图10 第7阶主振型

如图11所示为第8阶主振型，此时扭振主要发生在减速机输入齿轮轴，其与下分支系统直接啮合，引起下分支系统反向扭转振动，同时通过齿轮啮合带动上分支发生扭振。该频率主要影响减速机齿轮稳定性。

图11 第8阶主振型

3.2 直串式系统计算结果分析

直串式系统可检验分支式系统设计合理性，进一步确定主传动系统发生扭振时各零部件扭振状态。直串式系统固有频率见表5。

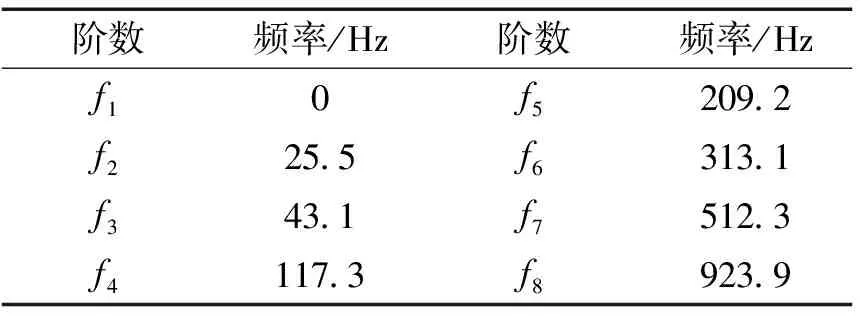
表5 直串式系统固有频率

如图12所示为直串式第2阶主振型，此振型表示减速机输出齿轮轴之后发生扭转变形，扁头和工作辊扭转振动幅值较大，该频率恰与分支式系统第2阶扭转振动振型相符，表明分支式系统和直串式系统结果一致。

图12 第2阶主振型

如图13所示为减速机输出轴轴头和扁头发生反向扭振，工作辊发生正向扭振，该主振型与分支系统第3阶振动模态相近。

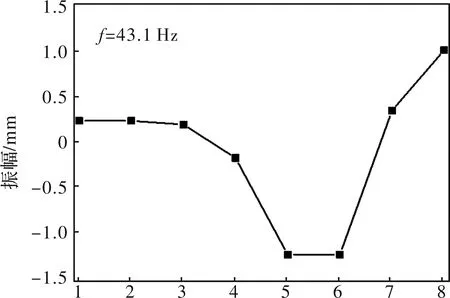
图13 第3阶主振型

如图14所示为第4阶主振型，传动系统下分支工作辊扁头发生正向扭振应变，工作辊发生反向扭振，该模态频率与分支式系统第4阶固有频率特征一致。

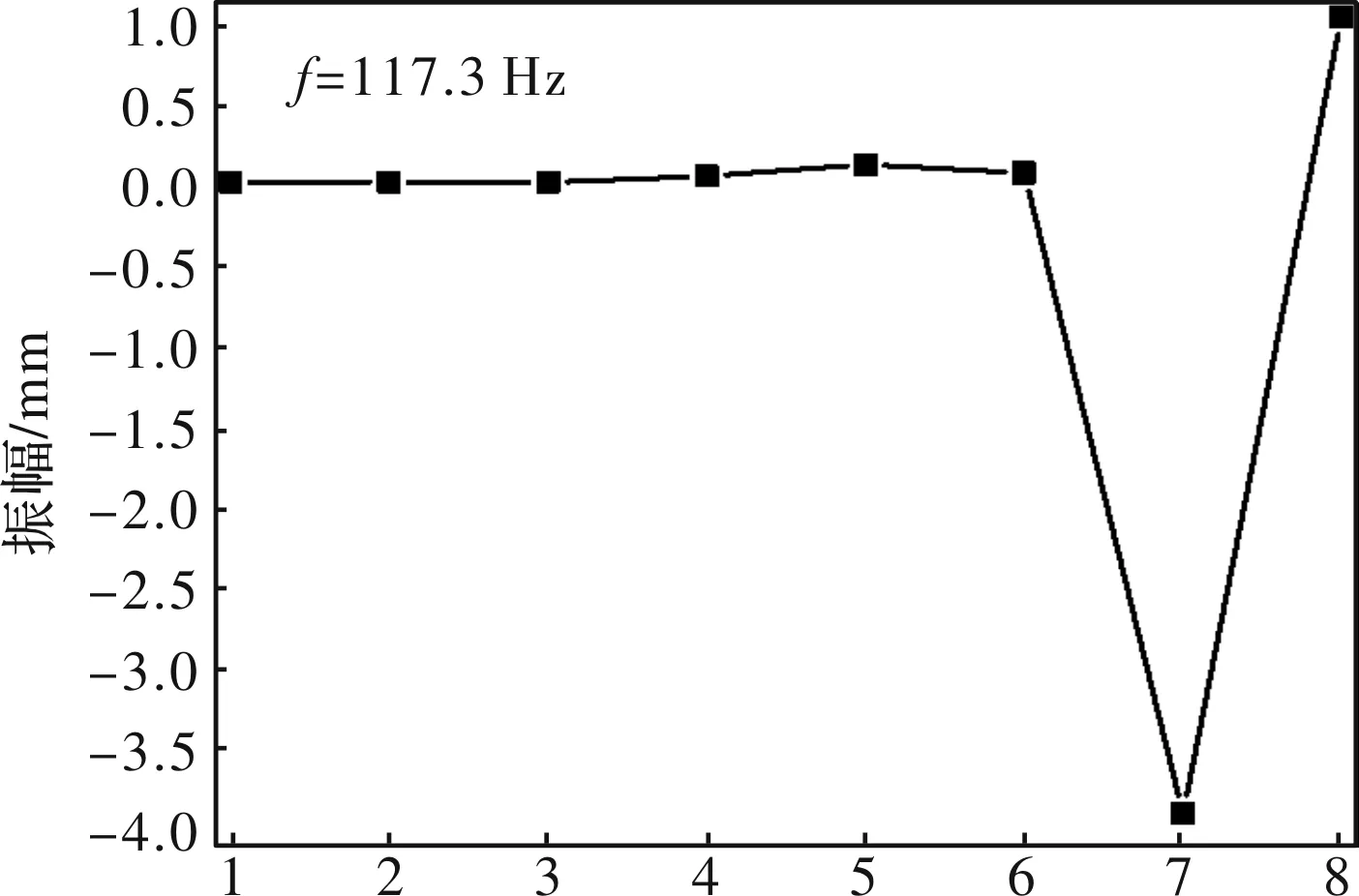
图14 第4阶主振型

如图15所示为第5阶主振型，由图15可以看出，下分支系统发生反向扭转振动，同时通过齿轮啮合带动上分支发生扭振。该频率状态与分支式系统中的第5阶固有频率一致。

图15 第5阶主振型

如图16所示为第6阶主振型，由图16可以看出，统扭转振动主要表现为主联轴器发生反向扭振，减速机主齿轮轴发生正向扭振，此时系统在二者连接位置发生较大扭转应变。该频率所示内容与分支式系统第6阶固有频率一致。

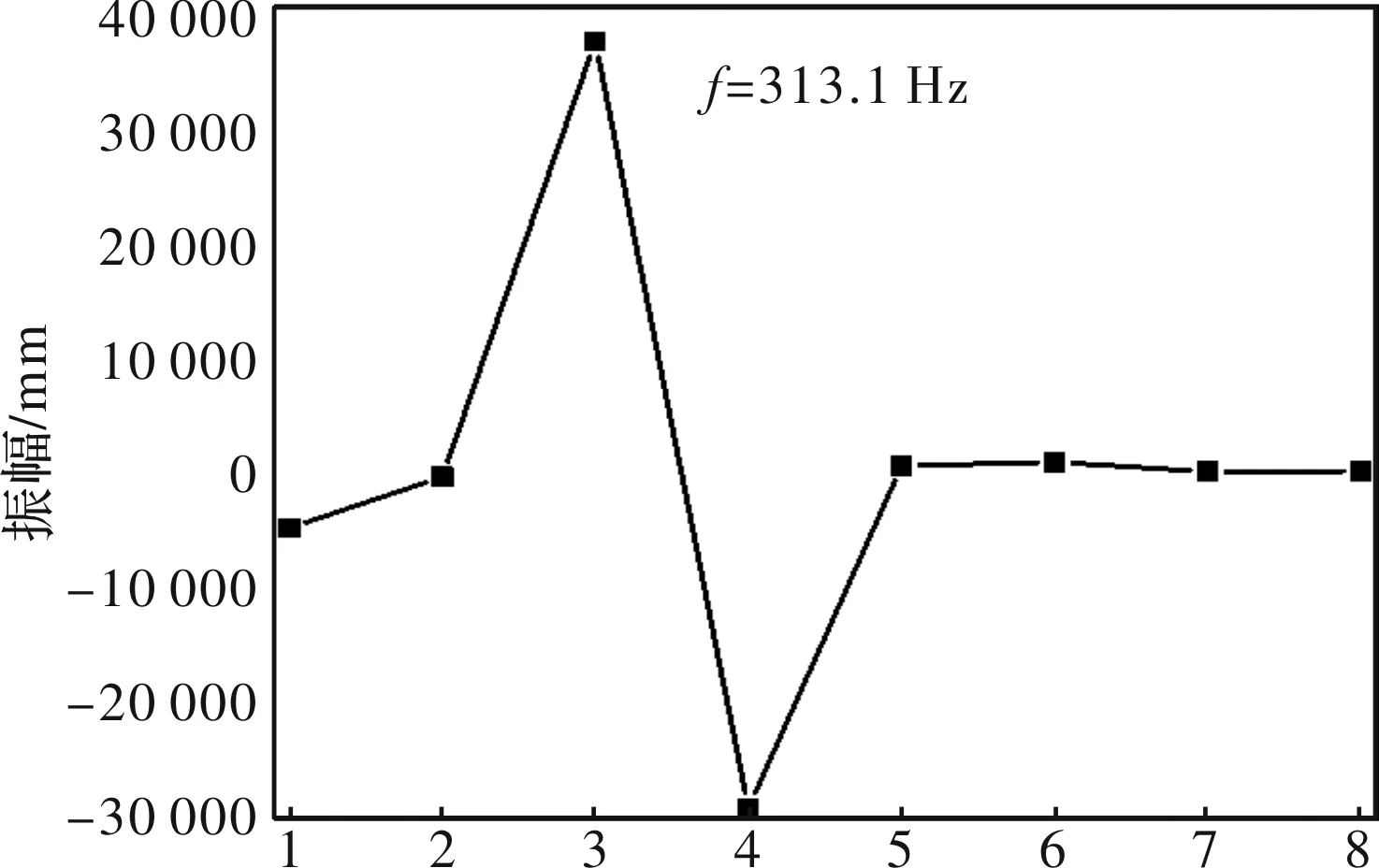
图16 第6阶主振型

如图17所示为512.35 Hz下系统振型图，生产状态下，接轴扭转刚度是系统最小的位置，其扭转将引起下分支同样发生扭振，该频率与分支式系统第7阶固有频率一致。如图18所示为第8阶主振型，此时主联轴器与电机连接位置应变最大。

图17 第7阶主振型

图18 第8阶主振型

由本文分析可以得出，分支式系统可以反映轧机上、下分支系统主要模态特征，而直串式系统将分支系统进一步简化，二者结构状态有所改变，整体来讲，两种模型均能反映系统固有特性。此外，扭转振动主要影响该系统中十字万向接轴扁头与工作辊连接位置、接轴与减速机分速齿轮轴连接位置，需要对两部分重点关注。

3.3 有限元计算结果分析

有限元模态分析结果中包含大量局部模态，即相邻频率为该传动系统下不同局部的固有频率，模态完全不同。表6为主传动系统整体在扭振方向上的主要扭振参数。此外，有限元考虑的模型全面，基本包含了所有理论计算结果。

表6 扭转方向各阶振型参与系数

如图19～图21所示为3.6 Hz、4.5 Hz、6.1 Hz下的振型图，最大扭转变形均出现在万向节出口处，3.6 Hz频率下参与系数和比值最大，在所有扭转振型中，此频率最容易引起外界激励达到共振状态，此外在此频率下主传动系统除主要的扭振变形外还伴随平动方向的变形，是一个耦合变形过程。

图19 3.6 Hz下主传动系统扭转振型

图20 4.5 Hz下主传动系统扭转振型

图21 6.1 Hz下主传动系统扭转振型

如图22所示振型图表现出整个扭转振动会转移到电机转子上，表明该频率下为电机转子的振动，由于忽略了电机外壳，此处有可能引起电机外壳在平动方向的位移，引起诸如地脚螺栓的松动等故障，因此安装时做好该部位的强度校核至关重要。

图22 10.6 Hz下主传动系统扭转振型

如图23所示为24.9 Hz下主传动系统扭转振型，由图23可知，在24.9 Hz下主传动系统主要的扭振变形转移到上接轴，与直串式的25.5 Hz和分支式的22 Hz频率下的主振型相似，因此在这几个频率下万向节是重点维护检查对象。

图23 24.9 Hz下主传动系统扭转振型

有限元分析中31.3 Hz频率下的主振型呈现与分支式28.9 Hz频率下相似的特征，都是上接轴及上轧辊出现较大扭转变形，如图24所示。同理，38.7 Hz频率下的主振型呈现与分支式33.8 Hz频率下相似的特征，都是从下接轴出现较大扭转变形，进而传递到下工作辊扁头处，同时输入端的大齿轮处也会发生一定扭转变形，如图25所示。两个主振型呈现对称特性，与分支式结果呈现相同特征。

图24 31.3 Hz下主传动系统扭转振型

图25 38.7 Hz下主传动系统扭转振型

有限元分析中79.8 Hz、108.1 Hz、121.5 Hz下的主振型分别对应分支式系统的77.9 Hz、108.9 Hz和直串式系统的117.3 Hz下的主振型。此三个频率下呈现相似的特征，如图26～图28所示，均是万向节的某个节点会出现应力集中现象，共振现象很可能导致万向节的运行精度，型钢质量受到较大影响。

图26 79.8 Hz下主传动系统扭转振型

图27 108.1 Hz下主传动系统扭转振型

图28 121.5 Hz下主传动系统扭转振型

4 结论

(1)分支式与直串式的模态分析结果一致，主要表现为齿轮啮合位置、万向接轴轴头输出位置以及扁头和工作辊连接位置发生扭振，容易产生应力集中而导致失效；

(2)有限元分析结果呈现大量局部模态，万向节处容易发生较大扭转变形，且一直传递到接轴处；齿轮啮合处产生扭转变形，尤其在输入端的大齿轮处；电机主联轴器与齿轮轴连接处是薄弱环节，是检查和维修重点；

(3)有限元分析结果无论与分支式还是直串式，均会在相邻频率呈现出相同的特征，有限元模型全面具体，分析结果涵盖了大部分扭振信息。