单元整体抓核心本质，深度学习促素养提升

丰玲玲 李真

摘 要：分数的相关知识对小学阶段的学生来说较难，以致学生在解决问题时不能准确地分析分数所表示的意义。文章从单元整体设计的视角剖析小学五年级上册“分数的意义”单元，以“计数单位”为主线，围绕“计数单位”设计一系列核心问题，让课堂教学随着问题层层深入，让单元知识在整体上一脉相承，让学生在主题的引领下开展深度学习，挖掘学科本质，突破知识难点，体会知识之间的内在联系，自主构建知识体系，发展核心素养。

关键词：单元整体;计数单位;深度学习;核心素养

作者简介：丰玲玲（1989—），女，北京市建华实验学校。

李真（1988—），女，北京市建华实验学校。

引 言

小学数学深度学习围绕具有挑战性的学习主题展开，而学习主题以数学学科核心内容为线索来确定[1]。“分数的意义”这一单元是小学数学“数与代数”领域的难点，分数的相关知识之所以难以理解，是因为分数意义的丰富性。孙京红在他的文章中指出了分数的多个含义，即比率——部分与整体的关系或两个量的关系，商——分数转化为除法之后运算的结果，分数可以转化为一个运算的过程，度量可以将分数理解为分数单位累积的结果[2]。分数仍然是数。郑毓信指出，面对数的扩展，我们不应将所涉及的各种数，包括原来的自然数以及后来学习的小数、分数等，看成互不相干的关系，而应将它们纳入同一个数系中[3]。教师应将学生在学习自然数的过程中形成的“数”的观念延续在分数教学中，这样有利于学生对“分数是数”这一理论的认可，有利于学生理解分数的意义，从而建构起分数与数之间的关系结构体系以及数内部的结构体系。因此，“分数的意义”这一单元的整体教学设计尤为重要，教师需要提炼出既能继承“数”的概念，又能贯穿整个单元学习的主线，以促进学生对分数含义的理解。

一、单元整体设计，一条主线，聚焦数学本质

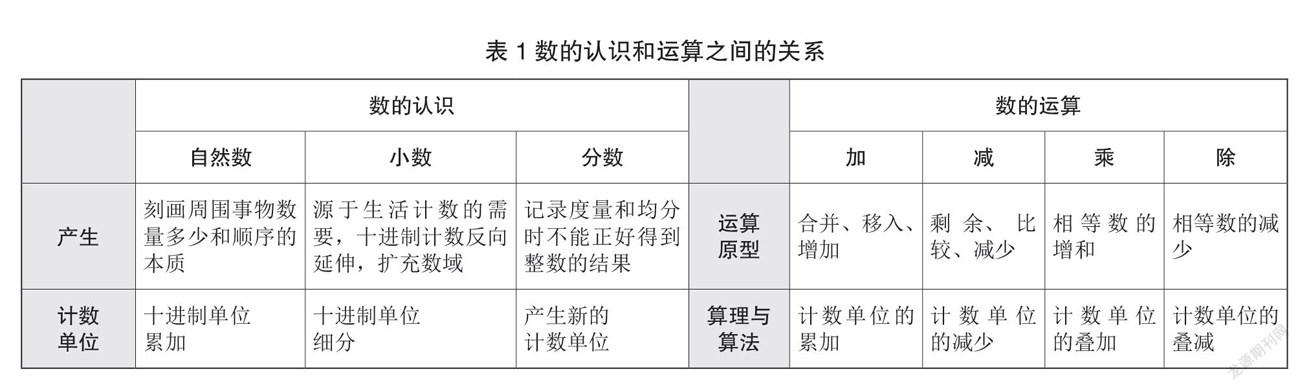
小学阶段的分数、自然数、小数的学习一脉相承、不可分割。数的概念主要有两种含义，即数本身的含义和比率。数本身的含义是相同计数单位的累加，比率是用“标准”去比较整体与部分的关系以及两个量之间的关系，虽然比较的标准是变化的，但是其本质和数的含义有相通之处。整数、小数乃至分数的产生都和“1”的关系非常紧密，即整体与部分，这种关系在分数的认识中体现得尤为明显。在数自然数的过程中，“1”是最基本的单位，以“1”为基础，每增加“1”就形成一个新的数。人们对整数的认识，从“1”开始，先有1个苹果，再有2、3、100、200、1000、2000个苹果。计数单位的累加，包含着部分与整体的关系。人们对小数的认识，也从“1”开始，先有1元钱，才有0.1、0.2、0.01、0.02元。计数单位的细分，包含着整体与部分的关系。方运加提到，1是数（shǔ）的开始，也是数（shù）的起始，之后是1+1，1+1+1，1+1+1+1，1+1+1+1+1……用已知学未知，靠的是“1”和“加”;数从“1”始，算从“1+1”始，数与运算就此展开。由此可见，“计数单位”是贯穿“数”的认识及运算始终的。无论是自然数、小数还是分数，其表示都是源于计数单位（如表1）。数的运算的本质是计数单位的累加或减少，人们对数的运算在认识数的过程中逐渐深入。数的意义支撑数的运算，数的运算加深人们对数的意义的理解。

分数也是数，其继承了自然数、小数的特点，又有自身的特殊之处。自然数和小数都是十进制的计数单位，自然数是十进制计数单位的累加，小数是十进制计数单位的细分。分数的计数单位却是千变万化的，让学生难以理解。教师可以先带领学生从单元整体的角度分析“分数的意义”单元中的知识点。从“分数的再认识（一）”这一课中理解分数单位的整体性、相对性;从“分数的再认识（二）”这一课中感受计数单位产生的必要性。“分数与除法”章节运用平均分产生计数单位，计数单位累加或者叠加（乘）得到分数，分数表示运算结果;“真分数和假分数”章节都是逐个计数单位累加的结果;“分数的基本性质”章节将不同计数单位的分数转化为相同计数单位进行运算;在“分数的大小”“最大公因数”“最小公倍数”以及“约分”这些章节中，分数的计数单位不同，分数大小不变。由此可见，分数的意义的核心是计数单位。基于此，教师可以计数单位作为“分数的意义”单元的学习主线，围绕主线设计一系列问题，逐个突破，层层深入。从数学学科本质上理解分数的意义，能够有效促进学生对分数多种含义的理解。教师深化学生对小学数学阶段所学分数内容的整体理解，能够促进学生进行知识体系的建构和方法的迁移，帮助学生在解决问题的过程中发展数学核心素养。

二、单元整体设计，系列问题，开展深度学习

深度学习的教学重点在于教师精心设计问题情境和学习任务，引发学生的认知冲突，组织学生进行深度探究的学习活动。单元整体教学设计利用知识的内在联系，创设问题情境，让每个问题都不是零散的，而是同一体系下直击核心本质。在“分数墙”一课中，学生突破以往以“小”量“大”的常规，借助长纸条量短纸条，在一次又一次的度量中创造新的分数单位，借助不同的分数单位度量相同的纸条可以得到不同的分数，形成分数墙。学生在自主创造分数墙的过程中感受不同的计数单位，“1”（长纸条）没有发生变化，每次创造新的计数单位进行度量，相同计数单位不断累加得到不同的分数。“真分数和假分数”一课用相同的分数单位表示更多的份数，使学生深度認识单位“1”，突破假分数的知识难点，理解假分数的含义，扩充分数墙。这面“墙”是学生思维创造的结果，是学生理解分数的直观材料，能为学生认识数轴提供有效支撑。在研究“分数的基本性质”时，学生借助分数墙继续研究，既延续使用学生熟悉的分数墙，又抛出关于分数墙的新问题，即如何在分数墙上找到相等的分数？学生快速找到自己熟悉的相等分数，逐渐发现相等分数之间的内在联系，即在分数墙上画一条竖线，会得到无数个相等的分数：2/3，4/6，8/12……每个分数的计数单位都不一样，表示的份数也不一样，但每一个分数都是其计数单位的累加，计数单位越小累加的份数越多。学生在一系列有关分数墙的问题的引导下，对分数的意义进行了深入学习。E2A5C13B-FE1C-4C88-83F8-674603A40AAE

三、单元整体设计，层层深入，体会本质联系

数学知识是人类实践活动的智慧结晶。教师在教学中要向学生展现数学知识的诞生历程，让学生理解和掌握数学知识的来龙去脉。教师还要引导学生将所学的数学知识进行优化整合，对相关知识进行串联，使之结构化、条理化，进而优化学生的认知结构，形成学一点懂一片、学一片会一面的强大知识迁移力和生成力。针对本单元的教学，教师从度量的角度出发，在每节课都围绕“计数单位”展开教学，让课与课之间层层深入，让学生不断深入理解分数的意义，理解“计数单位”。起始课“分数的意义（一）”借助两个量的关系，使学生认识到单位“1”是相对的，是指一个整体，同一个分数在不同的单位“1”下表示不同的含义，从而感悟单位“1”的重要性。“分数墙”一课用单位“1”不断地创造新的计数单位，让学生理解计数单位，累加计数单位，体会分数的完整性。在“真分数和假分数”一课中，学生深刻体会定义中“表示”的含义，5/4已经不能在“1”中取出来了，但可以表示5个1/4的累加，从而突破假分数的学习难点，再次理解相同计数单位的累加。“分数的基本性质”一课深入思考计数单位和表示的份数之间的变化关系，即计数单位越大，表示的份数越多，同一个分数用不同计数单位表示不同的份数，分数大小不变。在学习“分数与除法”时，学生毫不犹豫地用除法得到分数的结果，其本质是利用平均分得到计数单位，再将计数单位累加得到结果，其结果用分数表示。从单位“1”到平均分产生计数单位，再到计数单位累加，最后到计数单位和分数之间的关系，整个单元充分诠释了分数的概念。这样层层深入的学习过程，是学生体会计数单位的过程，理解分数意义的过程，构建分数概念的过程，也是将不同阶段数学知识联系起来的过程。

四、单元整体设计，一脉相承，发展核心素养

单元整体设计使我们不能仅思考一个单元或一部分的内容，而应立足小学阶段“数与代数”领域进行思考，将分数的初步认识和再认识有机地结合起来，将自然数、小数、分数置于同一条主线下思考，其广度贯穿整个“数”的认识，其深度直达“数”的核心本质。“数”的学习紧紧围绕核心主题——计数单位展开，学生在主题的统领下分段进行深度学习。分数是一个抽象的数学概念，计数单位对学生而言更是难以理解的数学核心要点。在三年级学生初次接触分数时，教师结合具体的“分一分”活动帮助学生整体把握部分和整体之间的关系，注重结合图形的直观性帮助学生理解分数。在学习活动中，学生借助平均分得到分数单位，与本单元“分数与除法”一课遥相呼应，由相同分数单位累加得到不同分数，初步理解分数的意义;在分数的大小比较中借助直观模型直接比较，进一步巩固分数的意义;在分数的加减法中直观地理解分数加减法的意义;由相同分数单位的累加或减少得到计算结果，再次理解分数的意义。教师在课堂中不仅要设计具体的问题情境，还要引导学生创造分数墙，将分数墙作为直观形象的模型，帮助学生理解分数的意义，促进学生对数学概念及其本质的感知、理解，以“计数单位”为主线，全面系统地构建“数”的知识体系。这样的直观模型，将复杂的数学概念简单化，使学生从本质上认识、理解了计数单位这一抽象核心概念与分数的实际意义。这样的学习过程既延续了对自然数、小数、分数的初步认识，又借助几何图形直观深入地剖析了数的意义，丰富了学生对数的认识，使学生在自主构建知识体系的过程中，提高数感和运算能力。

五、单元整体设计，实践作业，紧密联系生活

数学源于生活，并植根于生活，生活中处处有数学，数学蕴藏在生活中的每个角落。教师应以生活实践为依托，帮助学生将生活经验数学化，为学生的学习提供现实数据，使其体会生活中分数的意义。在本单元的学习中，学生搜集现实生活中的分数，如小学生睡眠时间占一天的，单位“1”是一天的时间，睡眠时间所占的比例是3个，初步感受计数单位，体会单位“1”和计数单位之间的关系;外婆的降压药早、中、晚各吃1粒，一板药是单位“1”，计数单位是，每天吃3个，一板药能吃3天，提醒家长下次买药的时间，以免中断;做蛋糕时每个蛋糕需要杯水，一杯水（50ml）是单位“1”，计数单位是杯水，一家四口需要做四个蛋糕，一共需要4个杯水。教师可以布置周末实践作业，让学生回家做蛋糕，并记录做蛋糕过程中的数据与其表示的意义，再让全班分享讨论，真正地将数学学习与生活紧密联系起来，将课堂上的数学知识应用于课后实践活动中。

结 语

教师以“计数单位”为核心本质统领分数的意义和运算的学习，贯通“分数的意义”和“分数的运算”之间的内在联系，注重对一类知识的基础内容的教学，使得同类知识之间的迁移条理化、清晰化，让学生在体会知识内在联系的过程中拓展学习内容，完善知识结构。这个完整的知识体系形成的过程其实就是学生结构化思维培养的过程。计数单位作为一个数学核心概念，本身比较抽象，不利于学生理解、掌握。教师教学时应结合学生生活中的实例，借助几何图形的直观性让学生亲身经历计数单位产生的过程，感受计数单位的价值，在學习过程中自主完善关于“数”的知识体系的建构。

[参考文献]

马云鹏.深度学习：走向核心素养（学科教学指南·小学数学）[M].北京：教育科学出版社，2019.

孙京红，张丹，李红云.分数意义教学的整体设计：“整体把握”理念下的系列活动设计[J].小学教学（数学版），2014（5）：11-14.

郑毓信.小学数学教育的理论与实践 小学数学教学180例[M].上海：华东师范大学出版社，2017.E2A5C13B-FE1C-4C88-83F8-674603A40AAE