刍议数学史背景试题的类型、特点及启示

摘    要：数学史在试题中的渗透是增添试卷人文韵味的一大举措，也是考查学生“四基”“四能”、数学阅读能力、数学核心素养等综合能力的需要.研究数学史背景试题，梳理其呈现方式“点缀呈现型、复制顺应型、材料阅读型、思想方法型”和特点“科学性、基础性、材料化、人文性”，能为教师提供参考和指导.其对教学的启示是要求教师：关注试题背景，设计变式练习;重视数学阅读，提升数学理解;拓展文化背景，巧用试题育人.

关键词：数学史;初中数学;中考试题

数学史作为数学文化的重要构成部分，在数学教学中发挥着独一无二的教育价值.研究证明，数学史具有知识之谐、方法之美、探究之乐、能力之助、文化之魅和德育之效的教育价值[1].数学史在试题中的渗透是增添试卷人文韵味的一大举措，也是考查学生“四基”“四能”、数学阅读能力、数学核心素养等综合能力的需要.研究数学史背景试题，既能为教师在中考数学文化的复习环节提供参考，又能指导教师在日常教学中对数学史的应用.下面，笔者以各地中考数学史背景试题为例，对该类问题分析、梳理，并提出教学启示.

一、数学史背景试题的类型

（一）点缀呈现型

点缀呈现型试题指仅为点缀而呈现与数学史相关的孤立图片或简单文字描述，且其与所考查的数学知识无关的试题.此类试题最常出现在“概率与统计”的考查中，大多是为增添历史元素而设计.

案例1   （2021年江苏盐城中考题）  圆周率π是无限不循环小数.历史上，祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前，超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现，随着π小数部分位数的增加，0～9这10个数字出现的频率趋于稳定，接近相同.

（1）从π的小数部分随机取出一个数字，估计数字是6的概率为____;

（2）某校进行校园文化建设，拟从以上4位科学家的画像（图略）中随机选用2幅，求其中有一幅是祖冲之的概率（用画树状图或列表方法求解）.

此题建构了算圆周率的历史背景，但其实质是考查“概率与统计”的内容.此题简述了圆周率π的研究历史，呈现了祖冲之的画像和《割圆密率捷法》的书影.就问题的解决而言，题干中“10个数字出现的频率趋于稳定”指出了随机取任意一个数都是等可能的，而其他要素几乎与问题是脱离的，即使将背景替换，也不影响问题的求解.并且祖冲之的画像及书影在该题中都是“可有可无”的，甚至书影与题干中的数学家都是毫不相关的，仅仅只是为了在试题中点缀以数学史元素.

（二）复制顺应型

复制顺应型试题指直接选用古代数学文献中的数学问题、历史名题等，或对这些数学问题进行一定的改编而形成的试题.此类试题最常出现在“数与代数”和“图形与几何”的考查中，尤其是涉及比例、方程、勾股定理等拥有丰富历史底蕴的数学内容.

案例2   （2021年湖南株洲中考题）《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”：“粟率五十，粝米三十……”（粟指带壳的谷子，粝米指糙米）其意为：“50单位的粟，可换得30单位的粝米……”问题：有3斗的粟（1斗=10升），若按照此“粟米之法”，则可以换得的粝米为（    ）.

A.1.8升    B.16升    C.18升    D.50升

案例3   （2021年山东淄博中考题）“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺.问：径几何？”用现在的几何语言表达即：如图1所示（编者注：以下出现的图序均有改动），CD为⊙O的直径，弦AB⊥CD，垂足为点E，CE=1寸，AB=10寸，则直径CD的长度是（    ）.

A.12寸    B.24寸    C.13寸    D.26寸

案例2、3都选自《九章算术》，其中案例2属于对“粟米之法”的改编应用，考查比例的计算;案例3属于“圆材埋壁”问题的复制呈现，考查垂径定理的应用.中考数学常会选用《九章算术》《算学启蒙》等古代文献中的问题来命题，这既能让学生感悟中国古代数学的成就，增强民族自信、文化自信，又能有针对性地考查相应的数学内容.

（三）材料阅读型

材料阅读型试题指题干中给出大量的数学史料，要求学生能够从史料中获得相关数学信息，进而解决数学问题的试题.此类试题的解答需要学生能够提取材料中的数学信息，在“综合与实践”部分较为常见.例如幻方类试题，学生在解答问题之前先要通过阅读材料了解幻方的规则，而后利用规则中所蕴含的数学原理去解决问题.

案例4   （2016年北京中考题）  百子回归图是由1，2，3，…，100无重复排列而成的正方形数表，它是一部数化的澳门简史，如：中央四位“19  99  12  20”标示澳门回归日期，最后一行中间两位“23  50”標示澳门面积……同时它也是十阶幻方，其每行10个数之和、每列10个数之和、每条对角线10个数之和均相等，则这个和为____.

此题以十阶幻方为试题背景，考查学生的阅读能力，以及应用知识解决问题的能力.学生需要在材料中获取十阶幻方的概念，从概念中抽象并提取出关键信息，即这个和与所有数的和之间的10倍关系，进而推得这个和是505.这类试题的考查内容并非常规的数学基本知识，更多的是学生个人能力（如数学阅读能力、问题分析能力等）的体现.

（四）思想方法型

思想方法型试题指以数学史中的思想方法为背景，引导学生利用该思想方法解决新问题的试题.这类试题的设计意图主要围绕对数学思想方法的理解与应用，即学生要具备一定的数学理解能力，能够理解题目中的数学思想方法，再在题干所给的示范或铺垫下，将数学思想方法应用于求解新的问题之中.在试题中最常出现的是出入相补法、割圆法等，考查的内容更指向数学知识的综合性应用.

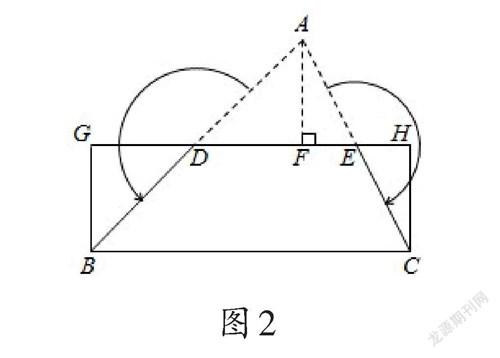
案例5   （2021年江苏常州中考题）中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法.如图2所示，在△ABC中，分别取AB，AC的中点D，E，连接DE，过点A作AF⊥DE，垂足为F，将△ABC分割后拼接成矩形BCHG.若DE=3，AF=2，则△ABC的面积是____.

此题给出了出入相补法的历史背景，引导学生将三角形面积转化为矩形面积，进而求解.不足之处在于，题目并没有解释什么是出入相补法、刘徽是如何证明三角形面积公式的.因此，即便学生在解题中应用了该方法，也无法对其形成深刻的认识.

二、数学史背景试题的特点

（一）科学性

就试题中史料的选取而言，此类试题最根本的特点就是科学性，即试题中的历史背景应有明确的出处，符合史实.在试题中，史料的呈现可以是简单的概括，也可以是图文并茂的详细说明，但前提是必须保证所选取数学史料的科学性，不能在试题中出现错误的、片面的、有误导性的内容.

（二）基础性

就试题考查的内容而言，基础性是此类试题的一大特点.由于试题的设计要从合适的数学史料出发，又受限于初中的数学内容，因此数学史背景试题相对集中于方程、勾股定理、圆等内容，并且大多是对数学基础性知识与能力的考查.

（三）材料化

就试题中史料的呈现方式而言，材料化是此类试题最常见的呈现方式.这里的材料是指与数学史相关的图片和文字的叙述.此类试题的开头大多会以文字的形式呈现相关史料内容，奠定试题的背景，部分试题还会附上相关历史图片.

（四）人文性

就试题的教育价值而言，以数学史为背景可以有效增添试题的人文性.数学史本身就属于人文素材，拥有着“文化之魅”与“德育之效”的教育价值.将数学史融入试题，学生在阅读题干的过程中就可以感悟数学历史、学习数学思想、拓宽文化视野，其中以中国传统数学历史为背景的试题还能达到弘扬传统文化、培养爱国情怀的育人目的.

三、教学启示

（一）关注试题背景，设计变式练习

在日常教学中，常会遇到数学史背景试题，教师在讲评时，要抓住试题背后的历史背景，并在此基础上进行变式练习，尽可能充分地呈现该背景下的不同变式，避免“就题论题”.例如，遇到三阶幻方的问题，教师可设计如下变式.

案例6   （2020年江苏盐城中考题）把1～9这9个数填入3×3方格中，使其任意一行、任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛书”，如图3所示，是世界上最早的“幻方”.如图4所示是仅可以看到部分数值的“九宫格”，则其中x的值为（    ）.

A.1   B.3  C.4  D.6

变式1：如图5所示的幻方中，a的值为____，m的值为____.

变式2：同案例4.

变式3：“幻圆”是一种类似于“幻方”的数学游戏，如图6所示，将−2，−4，−6，0，3，5，7，9分别填入图中的圆圈内，使横、竖，以及内、外两圈上的4个数字之和都相等.现已完成了部分填数，则图中x+y的值為____.

各地中考试题是初中教学中的“常客”，就案例6而言，难度不大，学生依据幻方的规则很容易就可将其补全.换言之，幻方中数字5的给出大大降低了试题难度，从而淡化了学生对幻方的深度认识，所以还需进一步变式扩充.变式1的目的是引导学生利用幻方的定义，得到“a+15=7+（−9）”，进而得到“m+（−9）=7+a”.通过变式1，学生能够意识到“各行（列、对角线）之和”并非是解题的关键，更重要的是对幻方定义的深入理解.设计变式2的目的，是让学生在整体的视角下求出“这个和”，即给出了“已知幻方内所有数，求各行（列、对角线）之和”的教学示范.变式3是类似于幻方的古代数学游戏“幻圆”，其规则类似于幻方，教师可以让学生在变式1、2的基础上自主思考.变式3的解决方法有两个：其一类似于变式1，先利用内圈与横排有公共数，得到“0+3=y+7”，求出y的值，再依次将剩下的数匹配对应，得到x的值;其二类似于变式2，先求出题目中的8个数字之和，得到横、竖、内、外圈上的4个数字之和都为6，再依次对照横排、内圈、竖排数字之和，得到x与y的值.

笔者通过以上三个变式，呈现了以幻方为背景的各类问题，以及与其相似的幻圆问题.这既能加深学生对该背景下试题的认识与理解，使其形成解决幻方问题的知识体系，又能让学生在变式探索中发展数学抽象、逻辑推理等数学核心素养.

（二）重视数学阅读，提升数学理解

数学史在试题中的融入分为显性与隐性两种，无论哪一种融入方式，都必然会在题干中出现许多材料.其中，点缀呈现型和复制顺应型试题，史料属于试题背景，并不会影响学生对问题的解决.而材料阅读型和思想方法型试题就侧重于考查学生对于史料中数学信息、数学思想方法的提取与理解，这就提示教师在教学中要重视对学生数学阅读能力与数学理解能力的培养.

以古代计数试题为例，题干会给出古代计数系统、计数符号等相关说明，要求学生提取出计数规律，运用类比推理思想来解决问题.当学生面对不熟悉的情境、大篇幅的文字时，自然会产生“畏难”心理，害怕去读题、解题.此时，教师应积极鼓励学生克服“畏难”心理，指导学生如何进行数学阅读，培养“边读边画”的解题习惯，让学生在一次读题的过程中找出关键信息，初步形成对问题的认识[2].紧接着，教师要引导学生建立关键信息与已有认知的联结，提取出与关键信息相关的数学知识、思想方法、解题经验等，将关键信息进行加工、深化，形成对问题的理解，进而解决问题.最后，教师小结并布置变式练习，帮助学生进一步巩固相关数学知识，积累解题经验.

（三）拓展文化背景，巧用试题育人

受限于试题的篇幅，数学史料在试题中的呈现更趋向于简洁化、概括化，甚至有将数学史隐性融入的试题.若对这些试题中的史料不加关注，就会丧失试题育人的契机，成为教学中的遗憾.例如，在遇到案例2、3这些选自《九章算术》的问题时，教师可以简单介绍《九章算术》的内容和文化价值，彰显文化魅力，并布置个性化探究任务，让学生在课后查阅《九章算术》中的问题，选择能够解决的问题进行摘录分享，充分激发学生的主观能动性，让学生在阅读整理中，提升数学素养、文化素养.若试题中隐性融入了历史上的数学思想方法，如“一元二次方程”几何解法，教师可先带领学生在问题的解决中，感受数学方法的巧妙，培养数形结合的意识，而后追本溯源，抓住试题中的历史背景，简单介绍相关历史，让学生学习古代数学家的思想与精神、感受数学文化的价值魅力，最终发挥数学史的“德育之效”[3]. [□][◢]

参考文献：

[1]王鑫，岳增成，汪晓勤.HPM研究的框架与进展[J].数学通报，2021（6）：7-12，19.

[2]黄贤明.聚焦核心素养   重视综合实践   提升数学阅读——以2021年苏州数学中考第27题为例[J].中学数学杂志，2021（12）：55-57.

[3]张安军.“古为今用”数学文化融入中考试题命制剖析——以“一元二次方程”几何解法为例[J].中学数学杂志，2020（6）：54-57.