遥感微纳卫星载荷平台高精度标定技术研究

崔阳，陈雪笛，姚小松，赵笙罡，王文川，王秋苹，马慧，李良成，潘超，王炳甲

（1.中国科学院微小卫星创新研究院，上海 201210；2.清华大学精密仪器系，北京 100084）

近年来，遥感微纳卫星凭借研制成本低、研制周期短、发射成本低和可快速组网等优势成为空间光学遥感的重要手段，从而受到各个应用用户和商业航天公司的青睐。对于遥感卫星而言，光学相机图像定位精度直接影响图像质量、高精度定量化。一般而言，卫星在轨利用星敏感器实现空间指向确定，再利用星敏感器与光学载荷之间的安装矩阵对光学载荷光轴指向进行转换和定位，这就对星敏感器与光学载荷之间安装矩阵的标定提出了一定的精度要求，如图1 所示。卫星发射前，在地面需要对星敏感器与光学载荷之间的安装矩阵进行标定，标定结果作为在轨确定光学载荷光轴指向的依据，地面主要通过高精度经纬仪、激光跟踪仪等高精度测量设备对星敏感器和光学载荷安装角度进行检测标定，地面标定精度一般为0.5″。但是卫星在发射时主动段力学负载较大，容易造成卫星、星敏感器和光学载荷结构发生一定的形变，相应会对星敏感器和光学载荷焦距、光轴指向产生一定的影像。此外，地面标定时卫星、光学载荷受9.8×10-3N 重力影响，而卫星在轨工作时处于空间微重力环境，卫星、光学载荷结构在轨会发生一定的形变；因此，卫星发射前后星敏感器和光学载荷光轴指向会发生一定的变化，光学载荷焦距在轨也会发生一定的变化。因此有必要开展遥感卫星在轨标定技术研究。

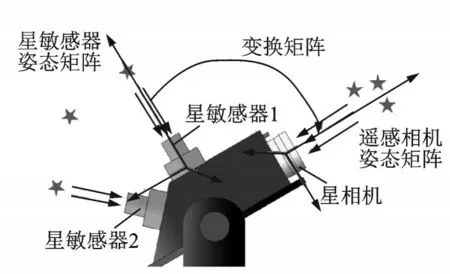
图1 星敏感器和光学相机的空间指向Fig.1 Pointing of star sensor and optical camera

基于以上问题，本文提出了一种光学遥感卫星在轨标定方法，即利用星敏感器和光学载荷在轨对恒星星点观测的方式实现在轨指向标定，以提高星敏感器和光学相机在轨空间指向精度。在轨标定分为自标定和互标定，其中自标定为利用光学载荷在轨观星的方式对成像焦距、光轴指向进行标定。互标定为利用光学载荷和星敏感器观星的方式，对光学载荷和星敏感器安装及指向信息在轨标定，即利用光学载荷对星敏感器指向进行标定（光学载荷视场较小，指向精度较星敏感器高），以提升星敏感器在轨指向精度。

1 光学载荷在轨自标定

1.1 光学载荷在轨自标定原理

遥感卫星采用在轨观星的方式进行载荷自标定，观星过程等效为经典的小孔成像模型［1-2］，如图2所示。图中f为载荷光学系统的焦距，π为载荷像平面，主点位于像平面的Os处，v̂i为i星在星表中唯一的方向矢量，i星经过相机成像后在恒星相机焦平面上的坐标为（xi，yi），其所对应成像测量方向向量为ŵi。

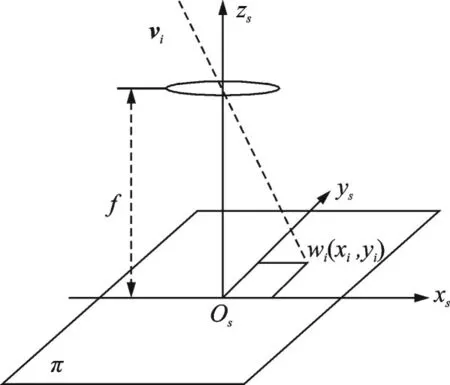
图2 观星小孔成像模型Fig.2 Typical configuration of remote sensing microsatellites

星在相机坐标系中的矢量［3］为

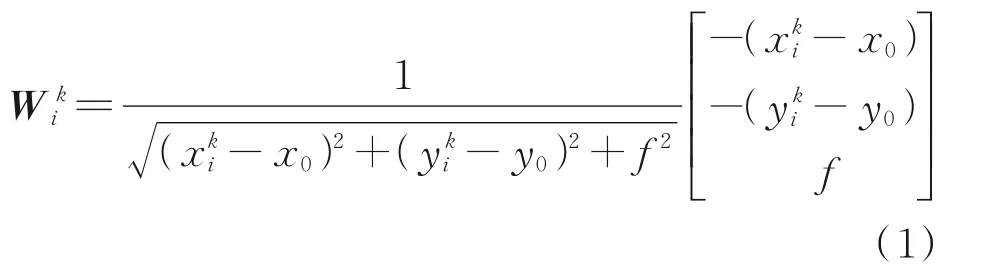
式中：（xik，yik）为第k帧星图中的i星点坐标，（x0，y0）为主点坐标，f为望远镜焦距，Wik为第k帧星图中i星点在成像坐标系中的矢量。

同时根据星图识别的结果，可以得到星点在J2000 惯性系下的星矢量［4］为

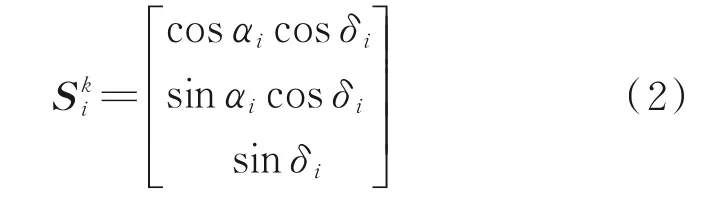
式中：(αi，δi)为i星点在J2000 惯性系下的赤纬度，根据光学遥感相机小孔成像原理可知，两颗星之间的角距维持不变

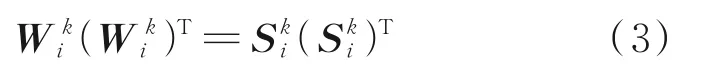
但由于星点位置随机误差、星敏感器误差以及相机内方参数误差导致式（3）存在偏差，从而可以得到角距测量值与参考值之间的残差，并获得残差矩阵［5］，利用最小二乘法对相机内方参数进行标定，如下式所示

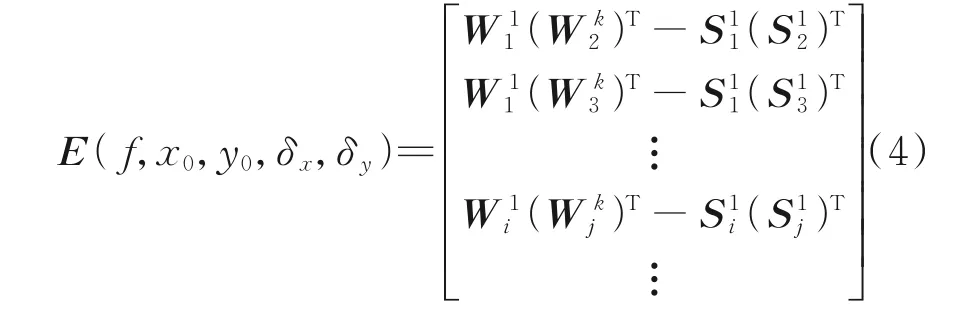
式中(αx，δy)为星点坐标由于畸变产生的坐标偏移量。设计光学载荷在轨自标定流程如图3 所示。

1.2 自标定误差分析

根据自标定流程，光学载荷自标定误差主要由星点位置坐标提取随机误差、星表误差、相机焦距以及光学畸变误差组成［6］。

1.2.1 星点位置随机误差

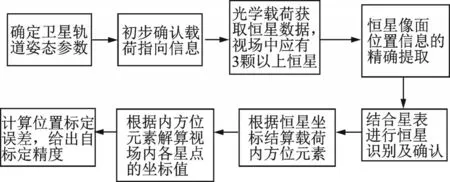
图3 光学载荷自标定流程Fig.3 Self calibration process of optical load

星点位置的随机误差主要由光学载荷探测器像面噪声、星点提取算法等因素决定。在地面外场实验过程中，由于星光需要穿过大气，因此将受到大气视宁度的影响；同时，在轨光学载荷一般焦距较长、像素分辨率较高，相应星像点会出现角秒级抖动，这对于亚角秒级的光学载荷而言是不容忽视的。

为了抑制星点位置的随机误差对自标定精度的影响，可利用光学载荷对星空进行连续多次成像，计算多帧星图中对应匹配的星点角距，将星点对角距平均值作为参考，利用最小二乘法对星点的位置坐标进行估计［7］，并对多帧星图星点位置进行滤波，可有效抑制星点的随机误差以及外场实验过程中大气视宁度的影响，实现星点高精度定心。

1.2.2 相机内方参数误差

（1）相机主点的误差

由于相机初始给定的主点信息并非其真实主点，假定(Δx0，Δy0)表示主点坐标的误差，那么星点在像面上的坐标为

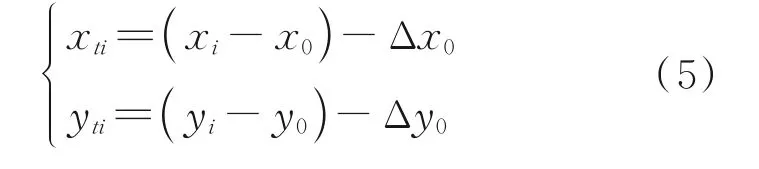
式中(xi，yi)为探测器提取得到的星点坐标位置。

（2）光学系统透镜误差

光学系统透镜安装存在偏移误差。透镜偏移带来的缩放比例误差为Sy，探测器旋转误差为θ，径向畸变（k1，k2）以及偏心畸变（p1，p2），可得到

式中(δxi，δyi)为相机主点误差和光学系统畸变所引起的坐标位置偏移。

1.2.2 相机焦距的误差

遥感光学卫星发射入轨后由于环境发生变化，光学相机焦距也会发生变化。设焦距变化量为Δf，则焦距变化为

根据式（8）及相机内方元素误差，可得到星点的星矢量在相机坐标系中的坐标［3］为

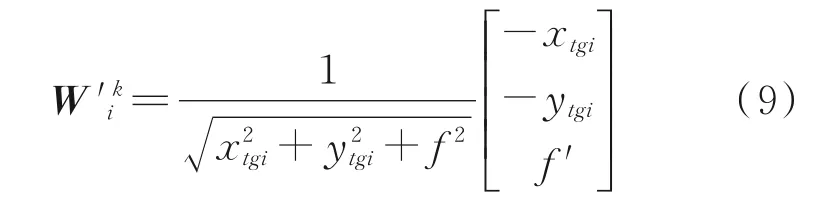
1.2.3 星表的误差

遥感卫星最常见的星表为Tycho-2 星表，该星表大约具有2 500 000 个星目标，其平均位置精度达到60″，平均自行精度达到2.5″/a，可进行光学载荷在轨高精度自标定［8］。

2 光学载荷与星敏感器在轨互标定

2.1 光学载荷在轨互标定原理

光学载荷与星敏感器在轨互标定指二者在轨光轴指向角度的标定，如图4 中的θ为二者光轴的夹角，其中星图A和星图B分别为星敏感器和光学载荷所观测到的星区。

图4 载荷和星敏感器互标定示意图Fig.4 Schematic diagram of mutual calibration between load and star sensor

为获得互标定角度θ，分别需要得到光学载荷和星敏感器的光轴指向信息，再解算二者光轴的夹角以及对应的标定精度。首先分别获取在标定时刻星敏感器和光学载荷星图成像数据，利用成像时刻卫星的位置、速度和时间参数对星图成像数据进行光行差修正，可分别解算获得星敏感器和光学载荷的光轴指向；再利用星敏感器和光学载荷光轴指向信息解算光轴夹角。互标定流程如图5 所示。

2.2 互标定误差分析

根据互标定流程，互标定误差可分为星敏感器和载荷成像时间的偏差、星敏感器与载荷自身的指向误差以及光行差效应带来的指向偏差。当进行地面外场实验时，由于星光光需穿过大气层，因此需要考虑大气层折射引起的偏差。

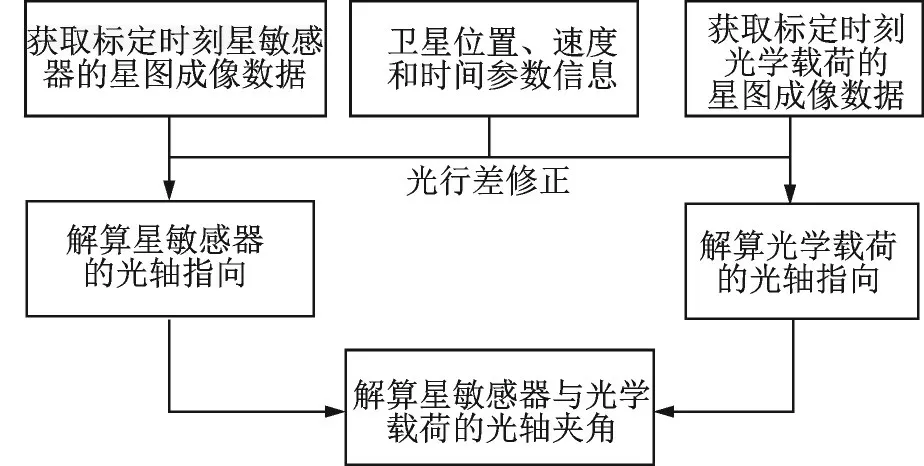
图5 星敏感器和光学载荷互标定流程Fig.5 Mutual calibration process of star sensor and load

2.2.1 星敏感器与载荷成像时间偏差

卫星在轨以一定的角速度转动，当星敏感器与光学载荷成像时间不一致时将会导致互标定出现偏差。目前星敏感器姿态四元数更新率可以达到10 Hz 以上，因此实际星敏感器与载荷成像星图的时间差不超过0.05 s，并且可以采用线性插值对星敏感器输出的四元数进行插值处理，以减少时间不同步带来的误差。同时，在进行在轨标定的过程中，需要保证卫星本体相对于惯性空间的角速度为零，以降低时间差的影响［9］。

2.2.2 光行差效应

光行差效应是指运动的观测者和同一地点静止的观测者观察到光的方向存在偏差的现象，如图6 所示。

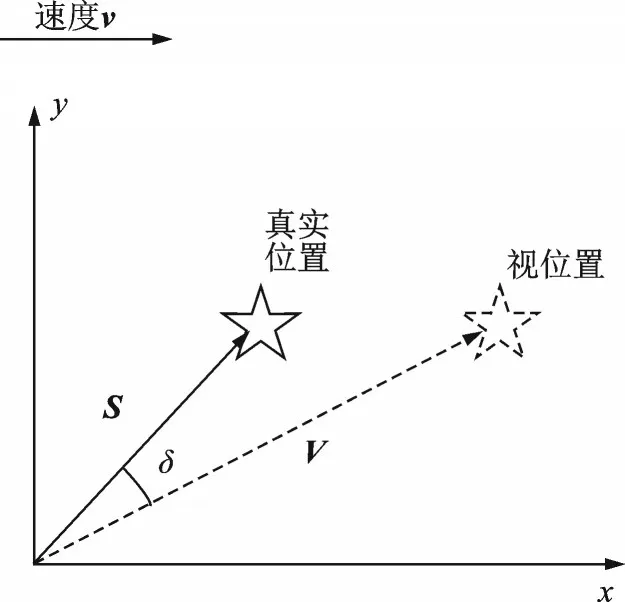
图6 光行差效应示意图Fig.6 Schematic diagram of aberration effect

图6 中，v表示物体在惯性坐标系下的运动速度，U、V分别表示星点在静止参考系与运动参考系下的观测矢量，δ表示光行差效应偏差角［10-11］。光行差效应的偏差角δ为

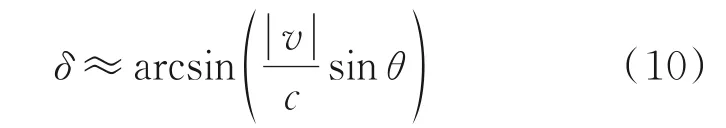
式中c为光速。对于近地轨道卫星，光行差效应的偏差角最大能够达到20.6″，并且由于星敏感器与光学载荷空间指向不同，二者存在的光行差效应偏差角也不相同，将导致互标出现偏差，因此需对光行差效应进行补偿。

2.2.3 大气折射补偿

大气折射是指直线前进的光线或电磁波在穿越大气层时，由于空气密度随高度变化而产生偏折的现象，如图7 所示。卫星在空间对星目标进行观测，因此不需要考虑大气折射，但是如果在外场地面实验，则需考虑大气折射因素。

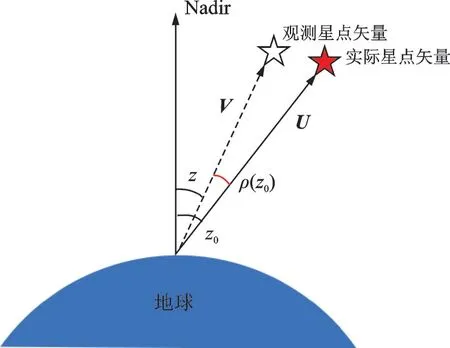
图7 大气折射效应示意图Fig.7 Schematic diagram of atmospheric refraction effect

其中大气折射的偏差角为

根据Owens［13］模型，可利用温度、大气压强以及大气相对湿度对大气折射率进行估计。

3 星敏感器与光学载荷地面标定实验

3.1 光学载荷地面自标定测试

光学载荷地面自标定测试结果分析以星区一为例，光学相机对星区一进行拍摄成像。地面星敏感器和光学相机（望远镜）安装如图8（a）所示，图8（b）为拍摄得到的星图星点。

图8（b）中连串的圆圈表示提取的恒星目标在像面上的移动轨迹，也说明此处的恒星目标有效；其他单个星点表示由于传感器等其他原因导致的误提取点目标。星图识别结果如表1 所示，可以看出，星图识别极限星等可达11.5 等星。

图8 光学载荷地面标定试验Fig.8 Ground calibration test of optical load

假设光学载荷对星空成像了N帧星图，首先每帧星图中均有M颗匹配星，如图9 所示，对1 星进行最小二乘定心［14］。

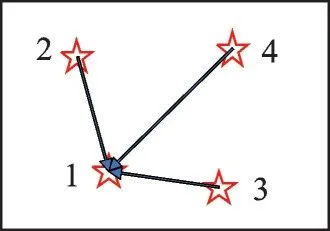
图9 帧内对星点1 进行定心Fig.9 Center Star 1 in frame

以1 星定心为例，建立测量计算匹配星角距与参考角距的误差矩阵［15］

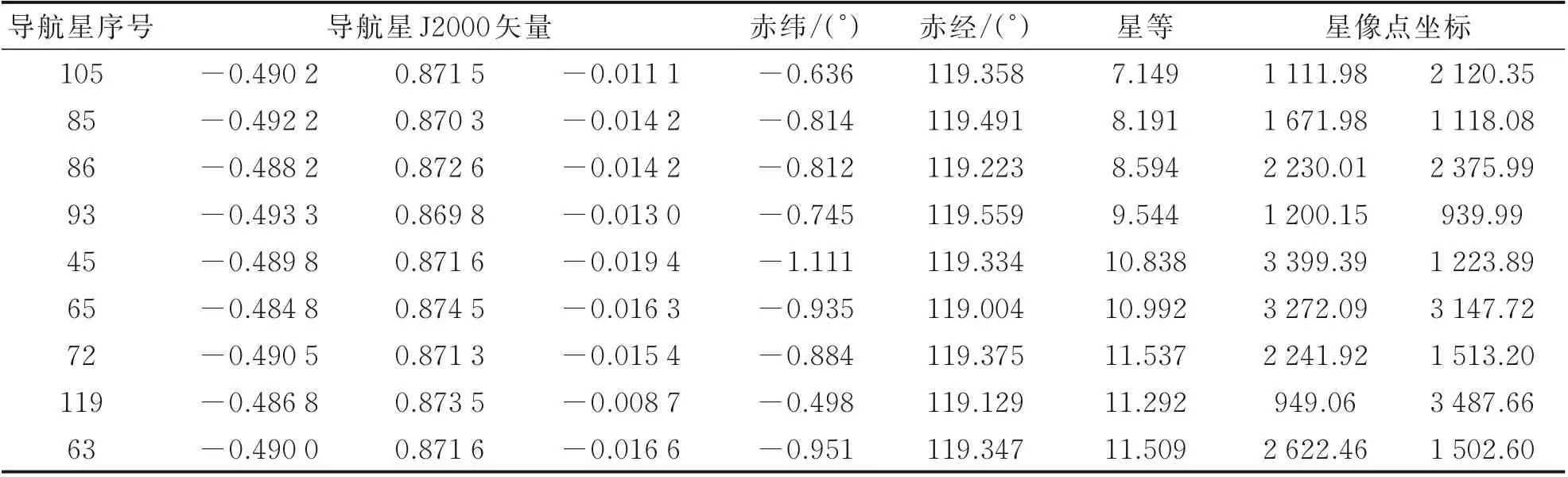
表1 光学载荷对星区一星图识别结果Table 1 Recognition results of optical load on star region Ι

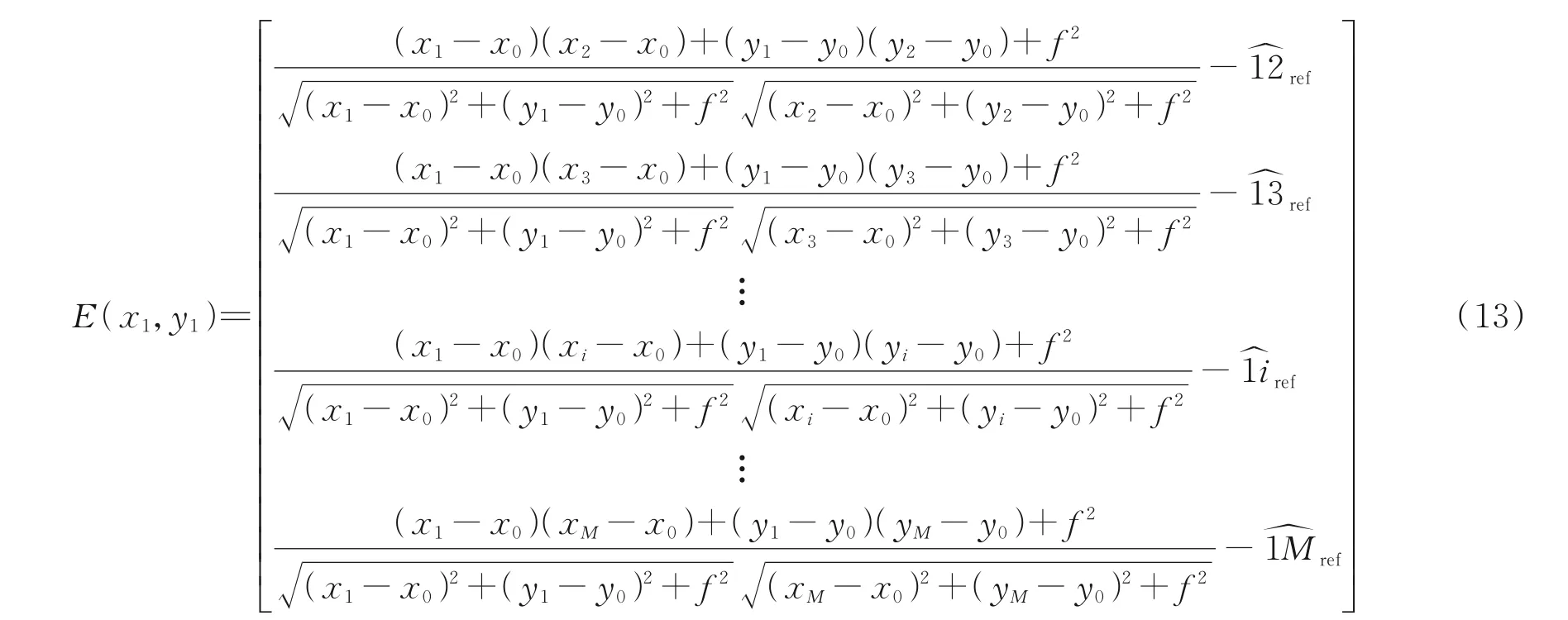
式中各参考角距的确定是利用多帧对应匹配星角距进行平均得到，这样可以在保留像面的畸变信息的情况下提高星点的位置精度

根据以上方法，利用星区一星图识别结果，进行光学载荷地面自标定，标定结果如图10 所示。图10（a）为焦距标定结果，得到焦距标定精度为0.48 mm（3σ，标定焦距为2 660.8 mm）；图10（b）为光轴指向自标定结果，自标定精度为0.198″（3σ），标定结果优于地面标定精度（约0.5″）。

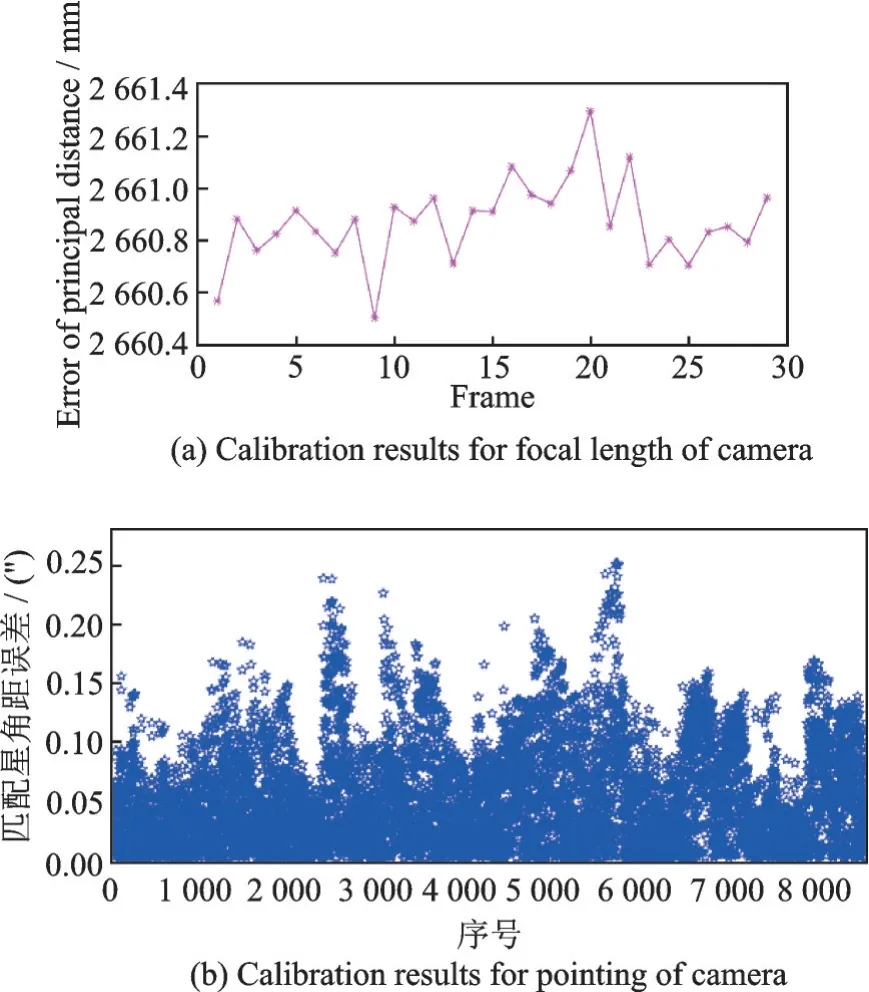
图10 光学载荷地面自标定结果Fig.10 Ground self-calibration results of optical load

3.2 星敏感器与载荷互标定测试

为了验证星敏感器和光学载荷互标定，需要对不同星区进行光学载荷指向成像。星区一的结果见3.1 节，星区二星图星点提取以及识别结果分析分别如图11 和表2 所示。

图11 星区二星图星点提取结果Fig.11 Star point extraction results of star map in star region Ⅱ

表2 星区二星图识别结果Table 2 Recognition results of star map in star regionⅡ

通过计算4 个星区成像期间星敏感器与光学相机夹角的变化，并对光行差效应以及大气折射进行补偿，可分别得到4 个星区内星敏感器与光学相机光轴夹角，如图12 所示。

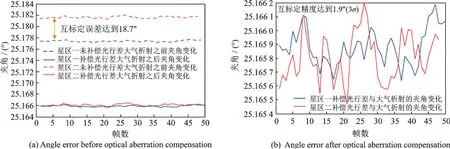
图12 光学相机与星敏感器夹角补偿前后Fig.12 Change of angle between optical camera and star sensor before and after compensation

通过图11 可以看出，通过2 个不同星区分别得到光学相机与星敏感器的夹角平均值为25.177 4°与25.1816°；测量精度分别为1.424 7″（3σ）与1.905 3″（3σ）。通过对其进行误差补偿，两个星区光学相机与星敏感器光轴夹角可收敛（补偿前互标定误差为18.7″）。可以看出，经过补偿后的光学相机与星敏感器光轴夹角精度大幅提升（优于2″）。

4 在轨测试及验证

4.1 光学载荷在轨自标定测试

图13 遥感微纳卫星对星区一连续成像星点提取结果Fig.13 Extraction results of continuous imaging star points in star regionⅠfrom remote sensing microsatellites

根据以上方法，利用在轨遥感微纳卫星对星区一进行遥感成像连续成像，如图13 所示。星区一光学载荷识别结果见表3。根据星区一得到的星点提取以及星图识别结果，结合星敏感器进行光学载荷标定，光学载荷焦距标定精度为0.1 mm（3σ），如图14（a）所示；光学载荷自标定精度为0.079 3″（3σ），如图14（b）所示，标定结果优于地面标定精度（约0.5″）。

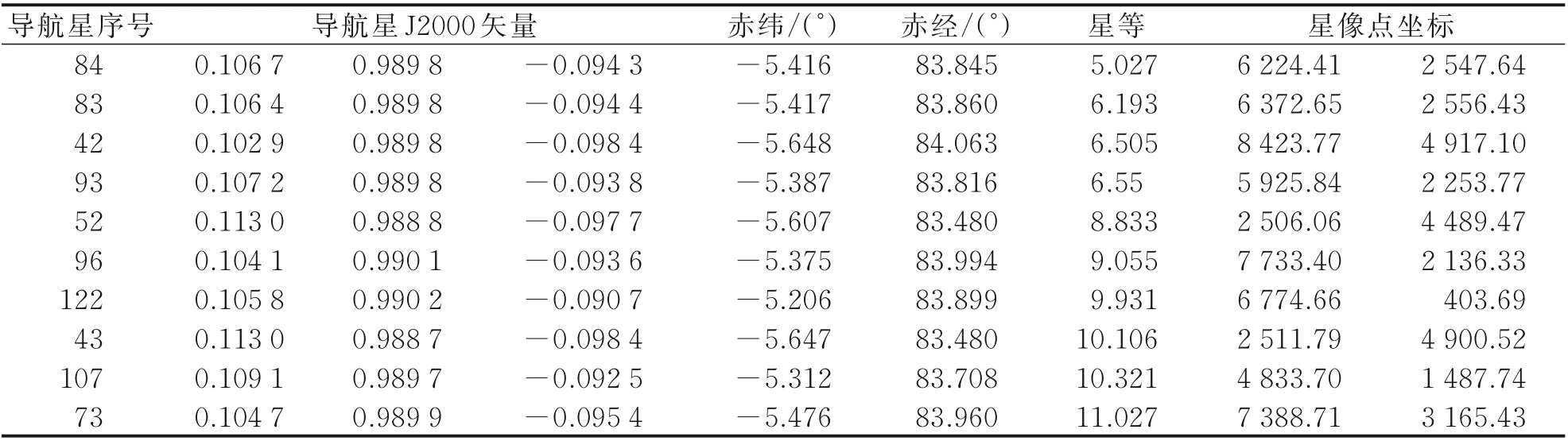
表3 光学载荷对星区一识别结果Table 3 Recognition results of optical load on star regionⅠ

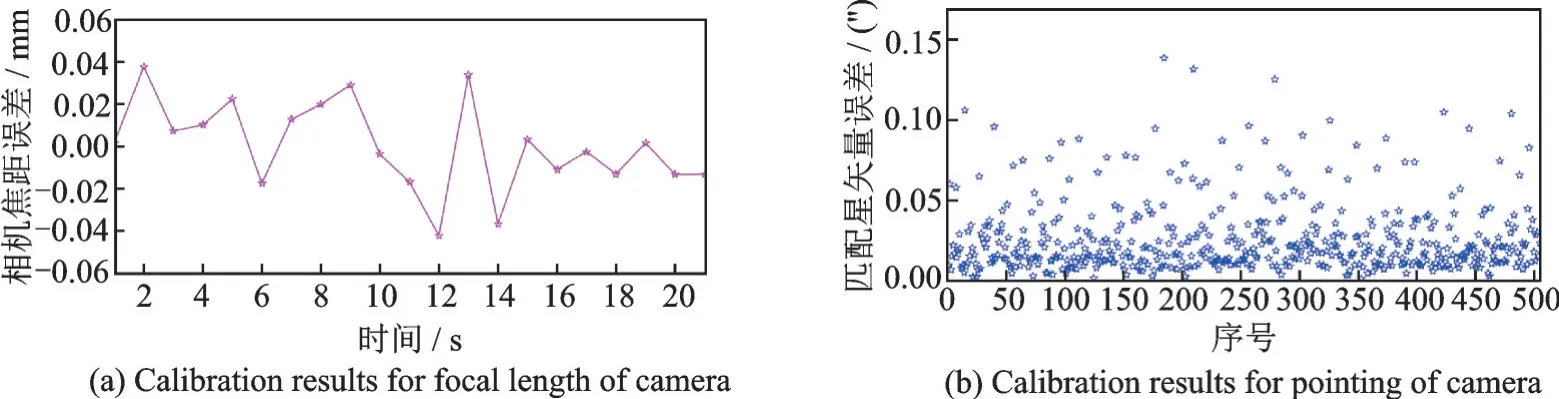
图14 载荷在轨自标定结果Fig.14 Self-calibration results of load on orbit

4.2 在轨互标定测试

利用在轨遥感微纳卫星进行多个星区拍摄成像，以验证互标定的有效性，表4 为星区二星图识别结果，可以得到星敏感器和光学载荷的光轴夹角，如图15 所示。可以看出，由于光行差效应的存在，在星区一和星区二成像的情况下，星敏感器与光学载荷的夹角并不相同。经过光行差补偿，光学载荷与星敏感器的光轴夹角得到很好的收敛。经过补偿后星敏感器与光学载荷的夹角精度为1.85″。

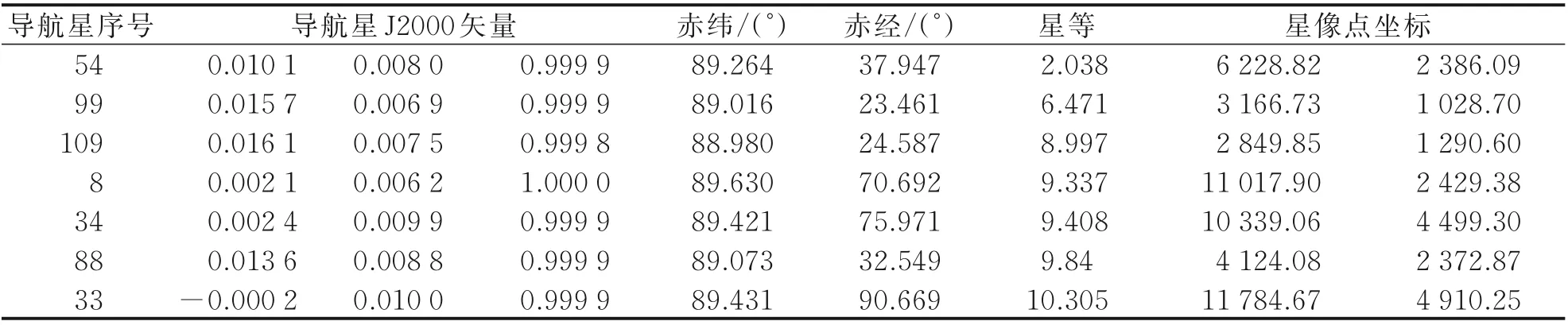
表4 星区一星图识别结果Table 4 Recognition results of star map in star regionⅠ

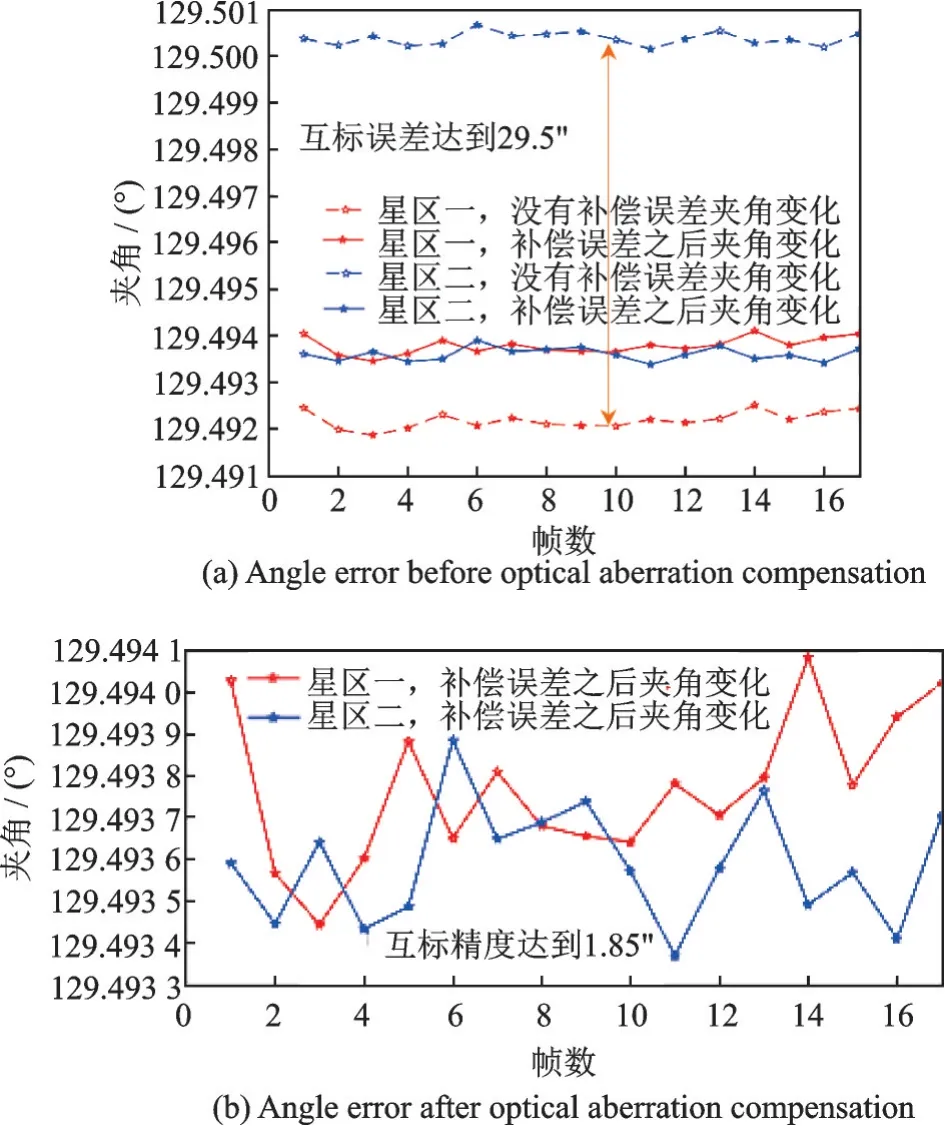
图15 载荷在轨互标定结果Fig.15 On-orbit calibration results of star sensor and optical load

5 结论

本文针对目前遥感微纳卫星在轨标定误差较大的问题，提出针对遥感微纳卫星在轨光学载荷自标定、光学载荷与星敏感器互标定方法，充分考虑了遥感卫星成像的各项误差和影响因素，并分别在地面和在轨进行实验验证。实验验证结果表明，利用光学载荷对恒星观测的方式实现自标定，光学载荷标定精度可达到0.2″（标定结果优于地面标定精度0.5″）；通过对地面大气折射误差进行补偿，可以使星敏感器和光学载荷夹角误差由18.7″降低至1.9″（3σ）；通过对在轨光行差大气折射误差进行补偿，可以使星敏感器和光学载荷夹角误差由29.5″降低至1.85″（3σ）。通过在轨自标定和互标定，可有效降低由于微纳卫星星敏感器精度较低引起的定姿和指向误差（利用光学载荷对低精度星敏感器进行标定和修正），以及提升遥感微纳卫星在轨成像质量。