自动钻铆装备的激光测量系统法向误差研究

沈 烨，田 威，李 波，廖文和，殷 飞

（1.南京航空航天大学机电学院，南京 210016；2.航空工业陕西飞机工业有限责任公司，汉中 723200）

随着中国C919 大飞机和四代机等新型号飞机研制进程的加快，航空制造业对于飞机制造的质量、效率等方面提出了更高的要求。同时，随着“工业4.0”与“智能制造2025”的提出与推进，实现飞机制造的数字化、柔性化和智能化已经成为当前航空制造业发展的必然趋势［1-3］。工业机器人和数控机床等自动钻铆系统作为飞机数字化制造的核心装备，在飞机装配中发挥了越来越重要的作用。

铆接是飞机装配使用最多的连接方式，工艺要求严格，孔垂直度是最为关键的技术指标之一。由于自动钻铆系统通过测量拟合出的理论平面法向量与实际制孔部位法向量存在偏差，因此系统的法向精度直接影响孔垂直度，进而影响铆接的质量和寿命。飞机蒙皮、壁板多为曲面，对法向的高精度测量提出了挑战。为了能够准确测量钻孔部位的法向，国内外学者做了大量研究工作，基于激光位移传感器的法向测量技术［4-6］和结构光视觉测量技术［7-9］是目前研究较多的两种法向测量方法。Tian等［10］采用4 个激光位移传感器对钻孔区域进行测量并拟合出平面，以平面法向近似代替钻孔部位曲面的法向，并给出了法向调整的数学模型，但其获取理论模型所需参数的过程较为繁琐，需反复更新公式验证效果，工程应用中耗时较长。李永超［11］也将制孔部位周边曲面近似为平面处理，采用最小二乘法标定了激光位移传感器在刀具坐标系下的位姿，利用激光测距传感器测量计算了法向偏差以调整机器人的位姿，但未考虑激光位移传感器本身的测量误差对法向误差的影响。Rao 等［12］采用结构光投影技术进行曲面的法向测量，提高了大曲率曲面的法向精度和鲁棒性，但其计算与分析复杂，工程应用性较差。Lee 等［13］采用多光束激光探头与电荷耦合器件（Charge coupled device，CCD）相机相结合的方法在三轴平台上测量自由曲面的位置和法向，能够感知曲面的大部分信息，计算出较为准确的法向；其工作原理同基于激光位移传感器的法向测量技术相似，但该方法的目的仅是测量曲面的法向，未给刀具的安装留下空间，加之其测量精度与平台的刚度有关，难以应用到机器人自动钻铆技术中。

尽管结构光视觉测量技术能够较为精确拟合曲面并计算出曲面法向，但由于需要处理大量点云信息，计算效率较低，难以应用于实际工程。因此目前的自动钻铆系统普遍采用的还是基于激光位移传感器的法向测量技术。采用激光位移传感器测量曲面法向，其法向误差受多种因素的影响，包括以平面法向近似替代曲面法向的原理性误差、激光位移传感器的位姿标定误差、激光位移传感器自身的测量误差和待测区域的表面质量等。其中影响激光位移传感器测量精度的因素又主要有景深误差［14］、倾角误差［15］、表面颜色［16］和表面粗糙度［17］等，孙彬等［14］研究了景深和倾角对测量精度的影响，并得出了量化的误差模型；雷斯聪等［18-19］针对基于激光位移传感器的法向测量技术，分析了以平面法向近似替代复杂曲面孔位法向时存在原理性误差的问题。Mentin 等［20］从传感器和激光二极管的定位不确定性入手，采用粒子群算法确定光源位置，降低了系统的总体测量误差。

为了优化法向测量模块的安装布局、提高法向精度，分析了激光位移传感器的测量精度对法向误差的影响，并在此基础上研究激光位移传感器的安装位置、安装角度、测量距离和法向调整角度对法向误差的影响程度。本文的主要工作如下：

（1）定量分析了传感器测量误差对孔位法向误差、位姿标定误差的影响，根据倾角误差产生的原理，构造了测量误差模型。

（2）分析了位姿标定误差并得出了误差分布规律。

1 激光法向测量技术

1.1 制孔部位法向测量原理

基于激光位移传感器的法向测量原理如图1所示，在刀尖点建立了刀具坐标系OXYZ，坐标系原点与刀尖点重合，Z轴与刀具轴线重合，刀具的进给方向为Z轴正方向。Mi（i= 1，2，3，4）为4 个激光位移传感器的测量零点，Ni（i=1，2，3，4）为激光束在钻孔表面的投射点，MiNi（i= 1，2，3，4）为激光束方向，G为待钻孔位置，为孔位法向，θ为孔位法向与刀具轴线的夹角。

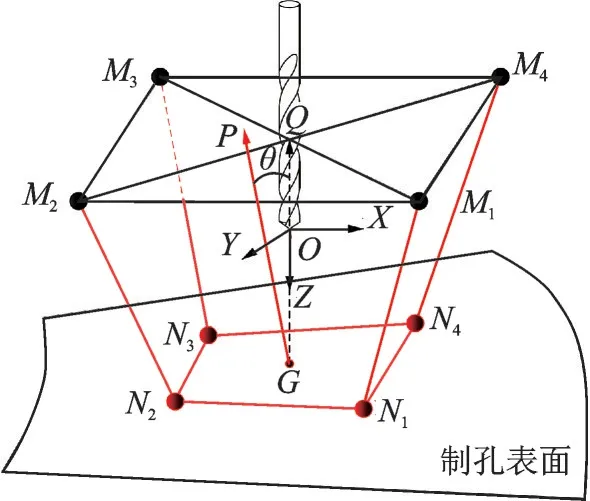
图1 法向测量示意图Fig.1 Schematic of normal direction measurement

采用平面模板法标定激光位移传感器的位姿，经过标定后，激光位移传感器的测量零点Mi（i=1，2，3，4）在刀具坐标系OXYZ下的坐标为（xi，yi，zi），激光束方向MiNi（i= 1，2，3，4）的单位矢量为（ai，bi，ci）。利用4 个激光位移传感器测得的数值di（i= 1，2，3，4）即可得到投射点Ni在刀具坐标系OXYZ下的坐标（xi+diai，yi+dibi，zi+dici）。采用特征值法可利用4 个投射点Ni拟合出一个平面，并得出平面的法向量。当制孔部位曲率较大，且激光投射区域较小时，可用拟合出的平面法向量近似代替制孔部位法向量。根据拟合的平面方程，可确定制孔部位单位法向量为（a，b，c）。

1.2 激光位移传感器测量误差分析

法向误差受多个因素的影响，本节主要分析激光位移传感器测量误差对法向误差的影响。假设待测量的制孔表面为理想的平面，激光位移传感器的标定没有误差，制孔表面的表面质量良好。激光位移传感器采用激光三角法测量原理，如图2（a）所示。测量距离D为

式中：s为相机靶面（即CCD 光敏面）上光斑的位移，L为参考点Z0的成像物距，L1为Z0点的成像像距，ω为入射光AZ0与反射光Z0O的夹角，θ为反射光Z0O与CCD 光敏面的夹角。L、L1、ω、θ均为系统的结构参数。

当传感器入射光束与测量面不垂直时，就会产生倾角误差［14］。当测量面倾角为β时，如图2（b）所示，将会引起激光光斑质心在线阵CCD 上的偏移，偏移量Δs可表示为

式中R为聚光透镜的半径。

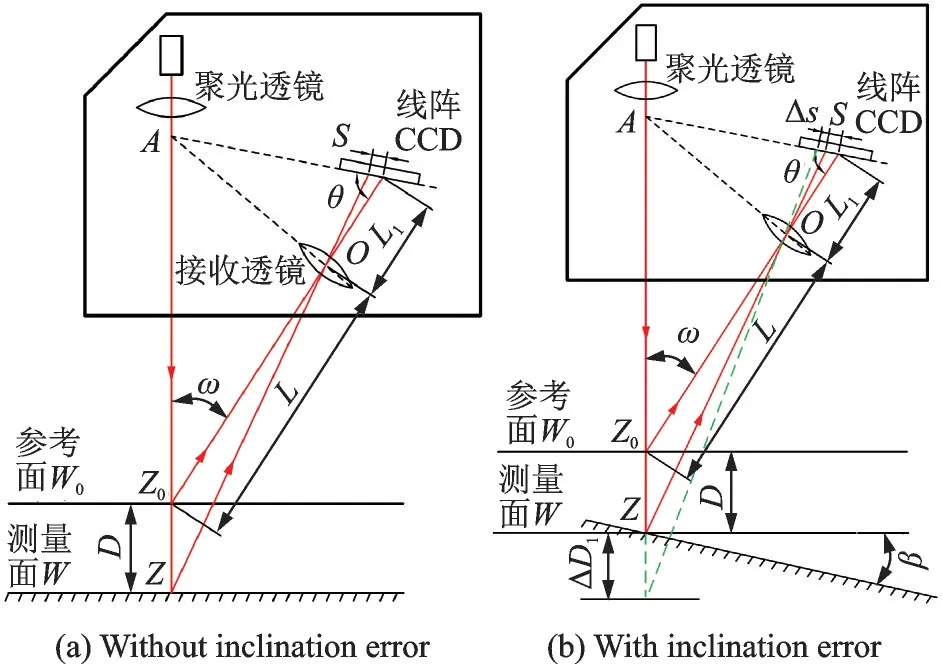
图2 激光三角测量原理图Fig.2 Schematic of laser triangulation method

为了保证被测对象点可以清晰地聚焦到线阵CCD 上，该激光束应该满足Scheimpflug 条件［19］

同时，L与L1应满足高斯成像定理

式中f为聚光透镜的焦距。

令s=Δs，可得到由于测量面倾斜引起的距离测量误差

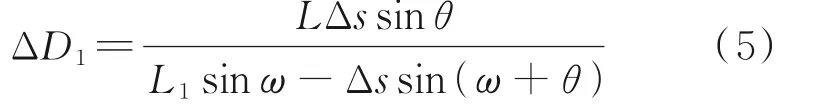
整理可得到距离测量误差ΔD1满足

相同型号的激光位移传感器具有相同的光路参数，即L、f、ω、R参数为定值，即

激光位移传感器的结构决定了其本身也存在线性误差ΔD2，ΔD2随着测量距离的增大而增大，对于同一型号的可调节量程的激光位移传感器，ΔD2随着量程的增大而增大，并且满足一定的函数关系。综合考虑以上两种因素，激光位移传感器的测量误差ΔD为

式中：当测量平面的法向相对激光入射光束顺时针转动时，ΔD1取正值；反之，ΔD1取负值。

1.3 激光位移传感器的布局分析

由于传感器入射光束与测量面不垂直时会产生倾角误差，4 个传感器的安装布局也会影响测量精度，从而影响法向精度。在实际应用中，由于钻铆末端压力脚的存在，4 个传感器只能分布在压力脚四周，因而有4 种安装布局方式，如图3 所示。分析每种布局的合理性，需要考虑以下因素：

（1）尽可能使激光光束与刀具轴线平行，并使4 束激光聚集在小区域内，以减小由于以平面法向近似替代复杂曲面孔位法向时存在的原理性误差。

（2）避免在安装时引入倾角误差，如图4 所示，OXYZ为固连在激光位移传感器上的坐标系，基于三角法测量原理的传感器，其自身的构造决定了在测量表面时，当被测面法向与X轴垂直时，激光位移传感器对该方向的倾斜不敏感，即认为不存在倾斜误差，而当被测面法向与Y轴垂直时，激光位移传感器对该方向的倾斜敏感，测量存在倾斜误差。

图3 激光位移传感器的4 种布局方式Fig.3 Four kinds of layout of laser displacement sensors

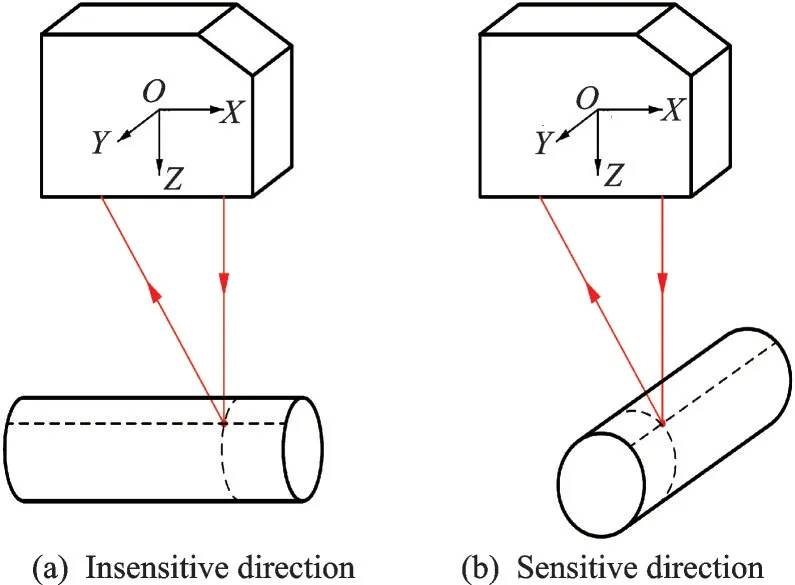
图4 倾角误差的敏感方向Fig.4 Sensitive direction of inclination error

（3）由于4 个激光位移传感器位置集中，应避免相互干扰。如图5 所示，点B为其他激光传感器的投射光斑，对于该传感器的测量可能会造成干扰，当点B与接收透镜的中心O的连线与线段ZZ0存在交点C时，会造成测量干扰，且点B距离线段ZZ0越近，干扰值越大，因此，在安装布局时，应避免这种情况。

图5 激光干扰示意图Fig.5 Diagram of laser disturbing

对于布局方式1，同侧的两束激光距离较远，光斑无法汇聚在较小区域内。而对于布局方式2、3、4，激光光斑都能在小范围内汇聚。但对于布局方式1、2、3，当激光光斑较集中时，均会存在相互干扰。尤其对于布局方式3，在安装布局时就引入了倾角误差。综合以上分析，最合理的布局是方式4：4 个传感器沿着刀具轴向圆周阵列分布，能使4个光斑均匀分布在孔位周围的小区域内；4 个传感器的安装倾斜角都是非敏感方向，不会在安装时引入倾角误差；4 束激光相互之间不共面，相互之间不存在干扰情况。

2 法向误差仿真分析

2.1 测量误差模型

实验采用的是Baumer 激光位移传感器，型号为OADM_12I6460_S35A。激光位移传感器出厂时，默认的测量范围为满量程（16～120 mm），可根据实际需求，设置合理的测量范围，以最大限度地提高测量分辨率。设置不同的测量范围，激光位移传感器的线性误差也不同，并且随着测量距离的增大而增大。法向找正实际应用中，由于法向调整角度相对较小（通常＜10°），4 个传感器的数值不会相差很大，因此根据该型号传感器固有的线性误差特性，当测量范围为50 mm，测量距离为30 mm ≤D＜80 mm 时，线性误差ΔD2近似满足以下函数关系

实际测量噪声可由随机函数生成

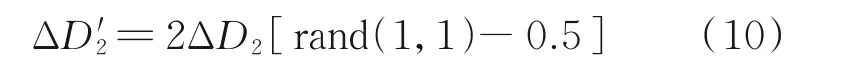
式中：rand（1，1）可生成（0，1）范围内的随机数，由此生成（-ΔD2，ΔD2）范围内的随机数，以此模拟激光位移传感器测量的线性误差。

该型号激光位移传感器的光路参数为：R=3 mm，L=30 mm，ω=35°，f=8 mm，由式（7），当测量距离D和被测面倾角β变化时，可计算出相应的倾角误差ΔD1。

根据线性误差ΔD2与距离D的关系，可在仿真中为测量距离D添加线性误差的模拟值ΔD'2。同时，由D和β可计算出相应的倾角误差ΔD1，则实际测量值D1为

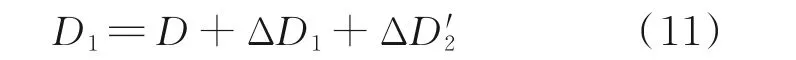
2.2 制孔表面法向误差

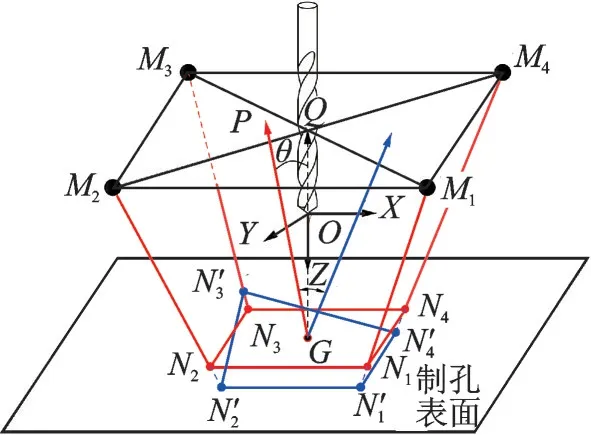
图6 测量误差造成的法向误差Fig.6 Normal error caused by measurement error

2.3 仿真结果与分析

2.3.1 测量距离对法向误差的影响

当聚焦为30 mm，安装角度为0°时，对于每个测量距离，计算100 组数据，得出法向误差平均值，仿真结果如图7 所示。

图7 法向误差随测量距离的变化曲线Fig.7 Curves of normal error with measured distance

由图7 可以看出，当测量距离D＜50 mm 时，法向误差无明显变化；当D＞50 mm 时，法向误差随着测量距离的增加而增加。因此理想的测量距离为50 mm 以内。

2.3.2 聚焦边长对法向误差的影响

当测量距离D分别为40 mm、50 mm、60 mm，安装角度为0°时，对于每个聚焦边长，计算100 组数据，得出法向误差平均值，仿真结果如图8所示。

图8 法向误差随聚焦边长的变化曲线Fig.8 Curves of normal error with focusing edge length

由图8 可知，当聚焦边长B在0～20 mm 内时，法向误差随着B的减小急剧增大。当B＞40 mm时，法向误差随着B的增大缓慢减小，即在这个区域内可以认为聚焦边长对法向误差没有影响。但为了尽量减小由于以平面代替曲面的原理性误差，应尽可能缩小聚焦区域边长，因此，将聚焦边长设置为20～40 mm 比较合理。

2.3.3 安装角度对法向误差的影响

当聚焦为30 mm，测量距离为50 mm 时，对于每个安装角度，计算100 组数据，得出法向误差平均值，仿真结果如图9 所示。

可以看出，随着安装角度的增大，法向误差缓慢减小，因此，适当增大安装角度有利于减小法向误差，且有利于4 个激光光斑在较小的测量距离时就能够汇聚。将安装角度设置为40°～60°比较合理。

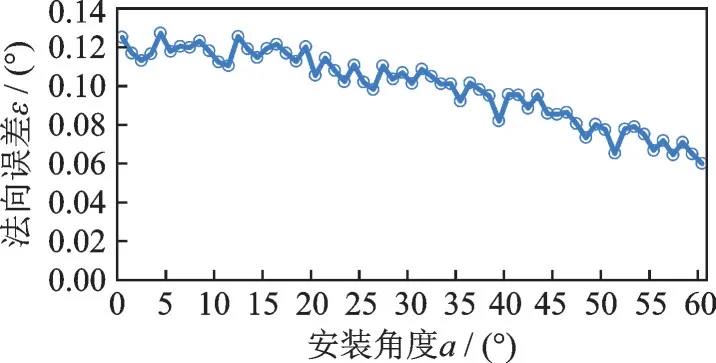
图9 法向误差随安装角度的变化曲线Fig.9 Curves of normal error with installation angle

2.3.4 法向调整角度对法向误差的影响

孔位法向与刀具轴线的初始夹角就是法向需要调整的角度，法向调整角度的大小也是影响激光位移传感器的测量精度的因素，因此也会影响法向误差。现研究法向调整角度对法向误差的影响。

当焦距为30 mm，安装角度为0°，测量距离为28 mm 时，改变法向调整角度的大小，计算100 组数据，得出法向误差平均值，仿真结果如图10所示。

图10 法向误差随法向调整角度的变化曲线Fig.10 Curves of normal error with normal adjustment angle

由图10 可以看出，当法向调整角度小于20°时，法向误差无明显变化；当法向调整角度大于25°时，法向误差随着法向调整角度的增大而明显增大。因此，在做工艺过程的离线轨迹编程时，应根据理论数模信息粗略计算好孔位法向，并在制孔时控制末端的位置和姿态，将刀具轴线与孔位法向的角度控制在20°以内。

2.3.5 参数优化后的法向误差

由于法向测量采用拟合平面法向近似替代曲面法向的方法，该方法本身就存在原理性误差，但只要曲面曲率较大，且选取的区域足够小，采用这种近似替代的方法也能较准确地测量出曲面的法向。因此，理论上应尽可能使激光聚焦在一个尽量小的区域内，但由于测量线性误差的存在，聚焦区域越小，测量误差对法向误差的影响越大，需综合考虑这两个因素的影响，合理选择聚焦区域大小。通过以上分析计算，给出一组优化后的参数：激光位移传感器的安装间距为70 mm，安装角度为45°，测量距离为40 mm，法向调整角度为0°，如图11 所示。计算100 组数据，仿真结果如图12 所示，法向误差平均值为0.073°，最大值为0.157°，此时聚焦区域边长B= 30 mm，是比较理想的情况。

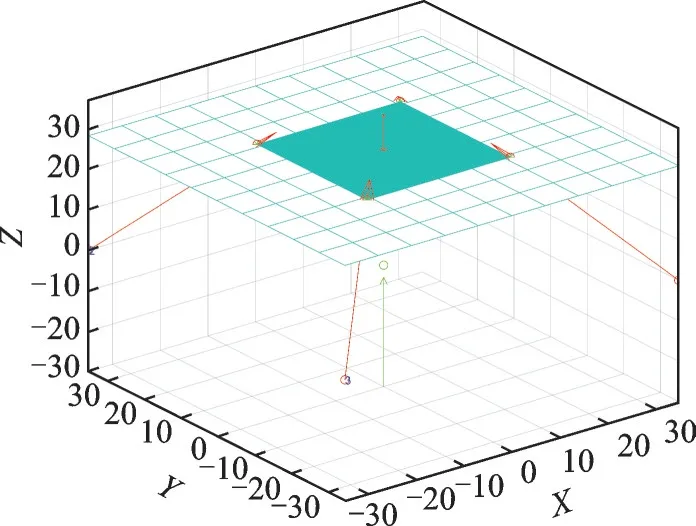
图11 参数优化后的法向测量示意图Fig.11 Schematic of normal measurement after parameter optimization

图12 参数优化后的法向误差Fig.12 Normal measurement error after parameter optimization

3 激光位移传感器位姿标定误差仿真分析

前面章节对于法向误差的分析都是建立在没有激光位移传感器位姿标定误差的基础之上的，然而在实际应用中，位姿标定误差是必然存在的，标定误差主要受测量误差等因素的影响。

3.1 位姿标定原理

对激光位移传感器的标定，实际上就是确定激光位移传感器的测量零点在刀具坐标系下的位置，以及激光束在刀具坐标系中的方向。位姿标定是利用已知参数的基准平面来标定的。将基准平面固定，法向测量模块的4 束激光投射到基准平面上，利用激光跟踪仪可以测量出该基准平面在刀具坐标系下的方程，将末端的位姿调整到不同的状态，测量出刀具坐标系在激光跟踪仪坐标系下的位姿，通过坐标变换可以得到基准平面在刀具坐标系下的位姿，并且记录激光位移传感器的读数。由于激光在基准平面上的投射点满足基准平面方程，而投射点的位置可以由激光位移传感器的位姿和读数计算出来，利用最小二乘法，解算6 组或6 组以上的数据，可以得出激光位移传感器在刀具坐标系下的位姿，即完成了位姿标定。

3.2 仿真结果与分析

现分析激光位移传感器自身的测量误差对位姿标定的影响，仿真步骤如下：

（1）给定激光位移传感器的理论安装位姿（安装间距70 mm，安装角度45°）。

（2）给定100 组基准平面方程。

（3）求出激光位移传感器的理论读数。

（4）根据测量误差模型，给理论读数添加测量误差，得到仿真的实际读数。

（5）根据100 组基准平面方程与实际读数，计算出激光位移传感器的实际安装位姿。

（6）比较理论安装位姿与实际安装位姿的差值，即是位姿标定的误差。

仿真得到的位姿标定数据如表1 所示。由表1分析标定误差数据可以发现，激光位移传感器位姿的6 个参数中，Z、C误差较小，而其他参数误差偏大，且有一定的规律性。对于位置参数X和Y，4个传感器的实际位置相对于理论位置，整体绕着Z轴的同一个方向旋转；对于姿态参数A和B，也有相同的规律。这是由于激光位移传感器的中心对称布局造成的。

表1 传感器位姿标定误差Table 1 Sensor pose calibration error

在选定了传感器布局方式以及安装位姿参数后，根据测量误差模型，对每个激光位移传感器进行测量误差补偿，可以提高位姿标定精度，从而提高制孔法向精度。

4 法向误差实验验证

为验证激光位移传感器安装参数优化的实际效果，搭建了法向测量实验平台，如图13 所示。法向测量模块的4 个激光位移传感器沿刀具轴线方向按照图3 中的方式4 均布安装在末端执行器的压力脚上，安装间距为70 mm，安装角度为45°，实验步骤如下：

（1）根据3.1 节所述的位姿标定原理，利用激光跟踪仪标定出4 个激光位移传感器在刀具坐标系下的位姿。

（2）将待测平面固定，控制机器人运动到待测面前方，使测量距离约为40 mm。

（3）将靶标球轻轻贴合在待测面上扫描出待测面点云，拟合出待测面的法向。

（4）将靶标座安装在刀柄上并放置靶标球，通过控制电主轴进给运动100 mm 并转动1 周，利用激光跟踪仪测量靶标球的位置，拟合出刀具轴线方向，测量出待测面法向与刀具轴线的夹角θ。

（5）记录激光位移传感器的示数，并通过位姿标定数据计算出待测面法向与刀具轴线的夹角θ'，从而得出法向误差ε=|θ-θ'|。

（6）控制机器人绕TCP 点在5°范围内旋转一定的角度，重复步骤（4、5）。

（7）重复步骤（6）的操作，最终得到20 个法向误差数据。

图13 实验平台Fig.13 Experimental platform

测量得到的结果如图14 所示，由图14 可以看出法向误差平均值为0.116°，最大值为0.173°。

图14 法向误差结果Fig.14 Results of normal error

5 结论

（1）建立了测量误差模型，进行了激光位移传感器布局分析与优化，得出圆周阵列分布是最为合理的布局。

（2）仿真分析了测量误差对位姿标定误差的影响，得出了误差分布规律。

（3）通过仿真定量分析了测量误差对孔位法向误差的影响，并给出了一组优化后的布局参数。在该组参数下，法向误差仿真结果的平均值为0.073°，最大值为0.157°；实验结果的平均值为0.116°，最大值为0.173°。

（4）本文的结果可为自动钻铆系统法向找正模块的设计、标定以及使用提供理论依据，从而提高制孔法向精度，保证孔垂直度要求，提高铆接质量和疲劳寿命。