基于区域生长和梯度阈值分割的路面裂缝提取算法

陈浩瀚 谢仁平 魏文红

(东莞理工学院 计算机科学与技术学院，广东东莞 523808)

混凝土路面裂缝是道路病害最早期的标志之一，不仅影响路面的平坦度以及稳定性，还存在着塌陷、破裂等安全隐患[1]。因此，道路维护部门需要及时根据裂缝的长度、宽度以及生长方向等情况，对路面的损害程度进行评估，制定相应的修复方案[2]。

传统的检测手段依赖于工作人员的现场实地测量，不但费时费力，且测量结果较主观。随着摄影设备及机器视觉算法发展，使得通过裂缝图像以及边缘提取算法来获取裂缝的实际信息成为一种可能[3-4]。常见的裂缝提取算法首先会将图像转化为灰度图，再利用其灰度特征将目标裂缝与背景色区分开。如大津法(OTSU)，通过计算前景色与背景色的最大类间方差将裂缝与背景分割开，但此方法只适用于灰度直方图具有双峰特征的图像[5-6]。当目标与背景色差异过大时，即灰度直方图存在多峰时，分割效果则不尽如人意。Canny算法利用图像的梯度信息提取裂缝，即根据合适的阈值将裂缝边缘快速、完整地提取，但如果图像留存了过多的噪声，许多与物体无关的边缘也会被提取出来[7-8]。尽管通过高斯平滑滤波可以滤除部分噪声，但图像中不平整、不规则的部分仍会被当成裂缝提取。区域生长算法则是利用一定条件下选择的像素点作为初始种子，再根据设定的判断准则判定周围的像素是否属于同一区域。合适的初始种子点和合理的判断准则是生成区域连续且完整的关键，否则，不仅会使算法效率降低，还会生成许多不属于裂缝的错误边缘信息[9-10]。

基于对以上算法优点与缺点的分析，本文提出一种基于区域生长和梯度阈值分割的裂缝提取算法，算法依据图像的梯度信息合理选择区域生长的种子点与判断准则提取裂缝的边缘信息，再通过梯度阈值分割去除错误的伪裂缝，实现快速、完整的路面裂缝提取。

1 基于梯度特征的区域生长算法

1.1 预处理和非极大值抑制

对于裂缝检测而言，无论是路面上的阴影、水渍或者污点，还是路面上不规则的纹理信息，都会对算法的检测结果产生影响。因此，必要的预处理可减少背景色噪声对后续算法结果的影响。预处理操作包括灰度化、平滑滤波和灰度阈值分割。灰度化可将图像从三通道的彩色图转化为单通道的灰度图，大大减少了图片存储的容量，且灰度化后裂缝的特征信息依旧明显。平滑滤波选用5×5的高斯滤波器，消除图像中的高斯噪声，使图像更加平滑[11]。灰度阈值分割利用图像中背景色与前景色差异，将图像中灰度值大于给定阈值的部分划分为白色，从而滤除大部分的背景色。

由于裂缝与背景的梯度信息存在明显差异，利用梯度变化便可以分割出裂缝的初始边缘信息。但裂缝周围梯度发生突变的像素点不止一个，如果直接将所有梯度突变的像素点都识别为边缘，那么所得到的边缘会不够准确。为了得到正确的裂缝边缘，可采用非极大值抑制的思想进行优化，即如果对于所识别的裂缝边缘像素点其属于梯度方向上的极大值，那么就认为其属于边缘点。Canny算法就包含了非极大值抑制的思想，通过选取合适的阈值分割点，便可获取大致的裂缝边缘[12]。

1.2 区域生长算法

区域生长算法是经典的图像算法之一，其中心思想是将一个区域中具有相似特征的像素点合并为一个区域。算法的主要步骤如下：

第一步：选取合适的初始种子点；

第二步：设定生长过程中种子点周围像素是否具有相似特征并进行合并的判断准则；

第三步：停止生长的判断准则。

从区域生长算法的中心思想可以看出，裂缝检测的关键在于初始点和判定准则应能很好的将前景色和背景色区分。一般而言，对于噪声较少、裂缝图像较为清晰的图片，其裂缝边缘的灰度值与背景色和裂缝内部区域具有明显差异，通过灰度值大小确定初始种子点和判定准则具有很好的效果[13]。但实际的裂缝图片可能存在阴影、黑点等灰度特征干扰，仅依靠灰度信息进行区域生长的算法缺乏很好的泛化性。文献[14]考虑到裂缝边缘像素的角度通常会大于90°，并以此作为判定准则合并周围成钝角的像素点，但该做法可能会漏掉裂缝的部分边缘。

虽然上述方法存在一定的局限性，但通过边缘像素的灰度值变化和梯度变化来确定初始种子点和判定准则仍具有一定可行性。以此为思路，作出裂缝边缘区域的梯度方向图(如图1)，其中，箭头的方向代表了梯度的方向，箭头的长度代表梯度幅值大小。观察图1中的裂缝边缘的梯度方向，可以看到裂缝边缘区域的梯度幅值和梯度方向具有明显的变化。因此，以裂缝的梯度幅值大小和梯度方向特征作为判定周围像素是否属于同一区域的准则。要获取图像的梯度方向特征，首先要获得图像在水平方向和垂直方向的梯度矩阵，采用3×3的Sobel一阶微分算子求取输入图像在横纵方向的梯度矩阵，则图像每个像素的梯度幅值可以表示为

图1 裂缝边缘区域的梯度方向

z=|gx|+|gy| ，

(1)

其中，gx表示水平方向的梯度，gy表示垂直方向的梯度。采用横、纵坐标方向的梯度绝对值之和代替传统的欧氏距离，牺牲了部分的精度换取更短的运行时间。由于图像中裂缝边缘的灰度有明显变化，而相邻像素点的灰度变化越大，梯度幅值就越大，越有可能是裂缝边缘区域的像素。因此，将梯度幅值矩阵按降序排序，并依次将每一点作为区域生长的起点。

图像梯度方向矩阵可以表示为

(2)

由于裂缝边缘相邻像素之间的梯度方向不会有很大突变，因此将种子点与周围8邻域的梯度方向作为生长的判断准则。当种子像素点的8邻域梯度方向存在相同或相近的像素点时，将其作为新的种子起点继续生长，直到所有的种子点生长完毕。考虑到裂缝生长可能存在多个方向，即一个像素点的8邻域存在多个梯度方向相同的点，因此在第一轮种子点区域生长完成后，以相同的种子点重复一次相同的生长操作，获得更加完整的边缘链。具体伪代码流程如下所示。

区域生长算法输入:梯度幅值矩阵M,梯度方向矩阵O,将M按降序排列得到的初始种子点S,方向阈值θ,状态标志I输出:若干条边缘链1.将S置于集合G,设置对应状态标志I(S)=02.for (num=0; num<2; num++) do3. for each S∈G do4. for each N∈Neighbourhood(S) 且I≠0 do5. if O(N)-O(S)<θ6. 将N加入G,设置I(N)=0,设置N为新的种子S7. end8. end9. 保存生成的边缘链10. end11.end

2 梯度阈值分割算法

区域生长算法获取的一系列边缘链，需要进一步验证其长度是否有意义，并且判断其是否为裂缝边缘，降低错误率。同时，对于长度过长的边缘链，需将其分段，并重新验证其长度的合理性和有效性。因此针对该问题，本文依据梯度阈值对所获取的边缘链进行再次验证分类。

2.1 裂缝的最小有效长度

首先需要定义裂缝的最小有效长度。不同的拍摄焦点，图像长度、宽度与裂缝长度存在一定的比例关系。选用文献[15]的裂缝数据集原图作为测试数据，该数据集由537张混凝土裂缝图像和对应语义分割标签图组成。经过大量测试，将裂缝的最小有效长度定义为

(3)

其中a和b表示输入图像的长度与宽度，α和β为修正系数，经过大量数据测试与分析，实验中选择α和β值分别为7.5和8。当所获得的边缘链长度小于最小有效长度时，则将其视为伪裂缝边缘并剔除。

2.2 梯度阈值分割

当所得的边缘链足够长时，考虑到所得边缘链中可能也存在长度无效的伪裂缝边缘，因此需要进一步的验证。由于裂缝具有梯度幅值明显变化的特点，设定横坐标步长为梯度幅值20，纵坐标为对应梯度幅值范围内的像素数的梯度直方图H，并定义如下表达式对长度过长的裂缝做进一步验证

(4)

(5)

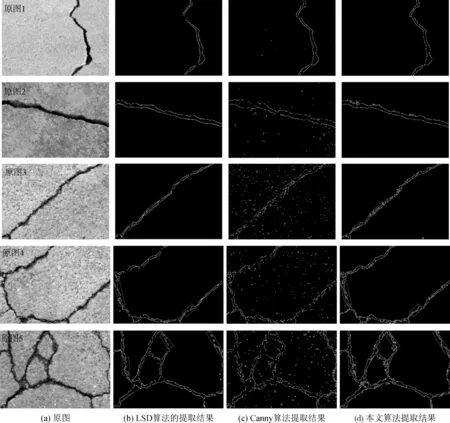
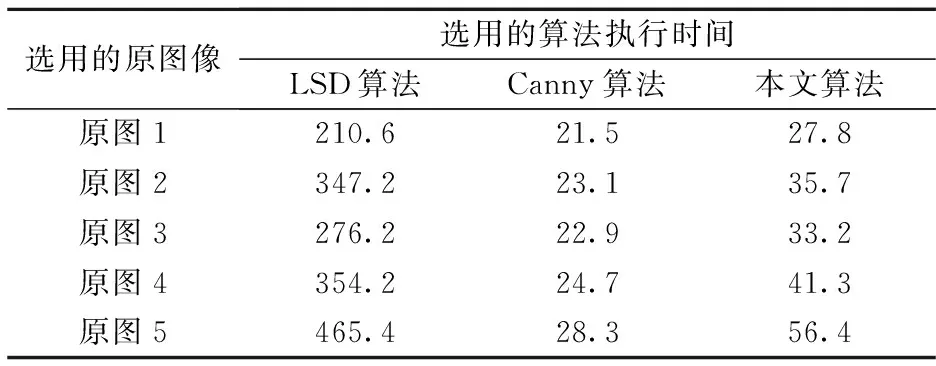
其中，t为实验测试后的梯度幅值阈值，经测试后本文中设定为60;d为当前测试边缘链的最小梯度幅值;ht和hd为梯度幅值为t和d时梯度直方图H所对应的值;m为最小有效长度;n为当前测试的边缘链长度。当P′>P时，认为该边缘链为正确的;当P′

3 实验结果分析

3.1 裂缝图像检测结果

为验证本文算法的有效性，将本文算法与Canny算法、LSD[16]进行实验对比。其中，Canny算法的主要思想是通过灰度图的梯度值进行非极大值抑制，再由梯度值进行双阈值检测和连接边缘；LSD算法的主要思想是通过灰度图的梯度值进行区域生长，获取矩形框内满足梯度条件的线段，最后由线段的特定点组成分割结果。三种算法的裂缝提取效果如图2所示。

由图2可以分析出，随着纵向的原图(a)中裂缝的轮廓变得逐渐复杂以及背景噪声逐渐增多，不同算法的最终裂缝提取结果差异较大。LSD算法在应对轮廓较为简单的裂缝时，可以较为完整的将裂缝的边缘提取出来。但如果裂缝不太规律、平整，存在大量弯曲的转折点，LSD算法提取的效果则不太理想，提取的裂缝边缘会有断开、不连续等缺陷。Canny算法在梯度特征明显、背景噪声较少的图像检测时，可以较好的提取出裂缝的边缘。但如果图像中梯度特征不明显、背景噪声较多，则图像中不规则纹理、污点也会被当成裂缝提取出来，错误率较高，效果较差。本文算法在裂缝轮廓变得复杂以及背景噪声逐渐增多的情况，仍能获得较完整的裂缝边缘。对比图2中的(b)列和(d)列，不难发现，(b)中LSD算法得到的第三幅到第五幅图中矩形框部分提取的裂缝边缘有明显断开痕迹，与之相反，而本文算法提取结果(d)中的第三幅到第五幅图的相应部分提取的边缘都更为连续、完整。

图2 裂缝提取算法对比

对图2不同算法的提取结果分别求取了准确率，三种算法的准确率结果如表1所示。由表1不难看出，随着原图图像裂缝的轮廓变得复杂以及背景噪声逐渐增多，各个算法的准确率均有所降低，但对比LSD算法和Canny算法的结果，本文算法均能拥有更高的准确率。因此，本文提出的基于区域生长和梯度阈值分割的路面裂缝提取算法，能更好地提取路面裂缝的边缘信息，并据此更准确地推算出检测裂缝的长度、宽度、面积等信息。

表1 三种算法的准确率对比

3.2 算法运行时间

算法的运行时间也是衡量算法优劣性的重要指标之一。在主频为2.90 GHz、内存16GB的台式机上，选取了图2中5张具有代表性的原图像进行测试，其裂缝的形状轮廓及背景噪声不断变得复杂和增多，分别测试其在LSD算法、Canny算法和本文算法下的运行时间，每张图片各测试5次，并取5次结果的平均值作为最终运行时间。由于Canny算法和本文算法由C++语言实现，而LSD算法由MATLAB语言实现，因此LSD算法的运行时间相对较长。表2列出了各算法的运行时间。

表2 三种算法的运行时间对比 ms

从表2的算法执行时间结果，并结合图2的原图可以看出，随着图片裂缝轮廓复杂程度和背景噪声的提高，各个算法的执行时间都会变长。其中，LSD算法耗费时间最长，且面对越复杂的图片，执行时间中增加的部分也远大于Canny算法和本文算法。三种算法中执行速度最快的是Canny算法，最复杂的裂缝原图5只花了28.3 ms便执行结束，但从图2可以看到，其执行结果充斥着大量噪声，裂缝边缘检测效果不佳。而本文算法具有同Canny算法相同数量级的执行时间，并且随着裂缝复杂度和背景噪声的提高，执行时间增加的部分远低于LSD算法。上述分析表明，本文算法能更好地提取路面裂缝边缘的同时，具有与Canny算法近似的执行效率。

4 结语

针对传统分割算法对路面裂缝信息提取时存在噪声较多、检测不完整等问题，笔者提出了一种将区域生长与梯度阈值分割相结合的路面裂缝提取算法。算法首先通过预处理和非极大值抑制来获取裂缝的大致边缘，再利用梯度幅值和梯度方向的区域生长算法来进一步优化裂缝的边缘信息，最后再通过梯度阈值分割算法去除掉不合理的裂缝。分析实验结果表明，该算法对不同类型的裂缝图像都可以获得较为理想的边缘信息，与现有的Canny算法和LSD算法相比，算法提取的边缘链更加完整可靠，具有一定的抗噪声能力和执行效率。