商用车总装配线排产模型应用

姚志刚，袁宇，李洁

（一汽解放汽车有限公司，吉林 长春 130011）

生产计划是制造企业生产管理的核心，是衡量企业管理水平的重要标准之一，只有制定科学合理的生产计划，才能保证生产资源的合理利用，提高生产效率。目前，生产计划员采用ERP 来制定生产计划，未将“生产效率”考虑在内。近年来，许多学者致力于生产计划建模和元启发式算法的研究。吕志民等［1］建立了中期生产计划模型，并用约束遗传算法嵌套线性规划的方法进行求解。付力［2］建立了以市场需求、工厂产能、成本为目标函数的生产计划模型。吴佳良［3］建立了以最小化成本为目标函数的数学模型并运用线性规划的方法进行求解。蒙秋男等［4］研究了混流线批次批量生产计划，并用蚁群算法进行求解。王军等［5］建立总生产计划模型并用动态规划的方法进行求解。邹泽桦等［6］用改进遗传算法求解柔性作业车间调度问题。徐建有等［7］针对单机调度问题提出多目标变邻域搜索算法。刘乐等［8］针对流水车间调度与外包问题，提出了混合变邻域搜索算法。上述学者大多只研究生产计划模型，或只研究算法，而实际排产中往往需要同时应用计划模型和算法。因此，文中对生产大纲计划建立数学模型并用CPLEX进行求解，针对车间作业计划，采用变邻域搜索算法（variable neighborhood search,VNS）进行求解。

1 生产大纲计划制定

1.1 主生产计划模型

以单位人时产能（units per hour per person,UUPH）作为生产效率的衡量指标，建立“量利人耗”最优科学排产模型，模型的目标函数是最大化UPPH，同时保证满足瓶颈资源、作业时间、作业人员、小时能耗、均衡排产和综合收益等约束。模型保证满足销售公司需求的“量”，同时保证每月获得的盈“利”，控制生产线使用的“人”员数量和能源消“耗”；输出结果是每日排产车型的品种及数量。目标函数表示最大化人均小时产出率：

式中：Xij为车型i在j天的排产数量，为函数自变量；H为日投入时间，单位为小时；β为月制度工作天数；M为生产线直准人员数量；Tti为车型i的节拍；OEE为产线综合可动率；bi为车型i的工时定额；η为月出勤率；Ei为车型i的单车能耗，λ 为小时能耗标准值；Qi为车型i的月生产数量；Si为车型i的销售价格；Ci为车型i的成本；P为利润指标；Iij为车型i第j天库存量；Isi为i车型安全库存量；Li为车型i日排产下限值；Ui为车型i日排产上限值。

1.2 生产任务分配模型

运行主生产计划模型后，将获得的生产任务分配到产线和班次上。分配原则为任务量均分原则和特殊产品加工原则，过程分为2步：1）产线分配，将生产任务分配到总装E线和总装F线；2）班次分配，将产线的生产任务分配到白班和夜班。

1.2.1 产线分配模型

以最小化E 线与F 线的作业时间差为目标函数，同时保证满足总量约束、特定指派约束和完成时间约束，模型输出的结果是每条产线每日排产车型的品种及数量。目标函数为

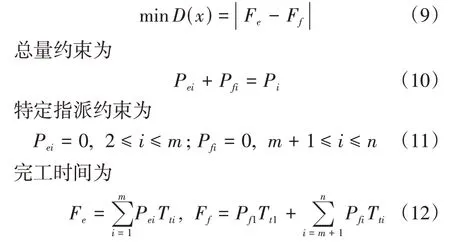
式中：Fe为E 线作业完成时间；Ff为F 线作业完成时间；Pei为车型i在E线的排产数量；Pfi为车型i在F 线的日排产数量；Pi为i车型的日排产数量。车型1在E线和F线均有生产，车型2～m在E线生产，车型（m+1）～n在F线生产。

1.2.2 E线班次分配模型

以最小化E 线白班与夜班的作业时间差为目标函数，同时保证满足取值范围约束、总量约束和完成时间约束，模型输出的结果是E线白班和夜班排产车型的品种及数量。目标函数为

式中：Fd为白班作业时间；Fn为夜班作业时间；Pi为i车型的日排产数量；Pdi为i车型在E 线白班排产数量；Pni为i车型在E线夜班排产数量。

总装E 线生产的所有车型白班和夜班都可以进行生产，故所有车型的数量在白班和夜班间是均分的。有时总数量不能被2整除，需添加取值范围约束进行平衡。

1.2.3 F线班次分配模型

以最小化F 线白班与夜班的作业时间差为目标函数，同时保证满足取值范围约束和完成时间约束，模型输出的结果是F线白班和夜班排产车型的品种及数量。目标函数为

2 车间作业计划的制定

生产任务分配完成后，确定生产顺序，即生产调度。调度问题是NP-hard问题，传统运筹学方法如分支定界法难以求解大规模调度问题，模拟自然和社会行为的元启发式算法在求解调度问题上取得了优异的成绩。VNS 与遗传算法、蚁群算法、模拟退火法相比，具有参数少、收敛速度快、求解效果好等优点。根据实际情况，采用VNS进行求解：

1）编码 为了便于理解和计算，采用自然数进行编码，每个自然数代表1种车型，1组自然数列代表车型序列。图1 展示的条码表示总装配线按顺序装配1车型3个，2车型2个，3车型2个。

图1 车型序列图

2）初始化 以原生产计划为初始解。

3）邻域搜索 此阶段为算法的发散阶段，主要有交换、插入、颠倒3种邻域操作。

4）更新解 若新解优于原解则进行解的更新；否则，为避免算法陷入局部最优，以小概率进行解的更新。更新解后记录算法的历史最佳解。

5）终止判断 若迭代次数没达到最大迭代次数，则返回步骤3），否则进入步骤6）。

6）解码 将编码序列转换成生产任务单。

7）输出最优解 输出最优解，算法结束。

3 科学排产的应用

3.1 主生产计划

以某总装车间某月生产任务为例，应用CPLEX，根据分支定界原理，求解各车型最优日排产量，指导生产大纲排产。按照每个月20 d、每天有效作业21 h，求出日排产数量如表1所示。尝试缩短每班的工作时间，即每天有效作业时间为19.4 h，求出日排产数量如表2所示。结果表明，调整各车型每日的生产数量，可以实现工人每天早下班48 min，人时产能提升8.24%。

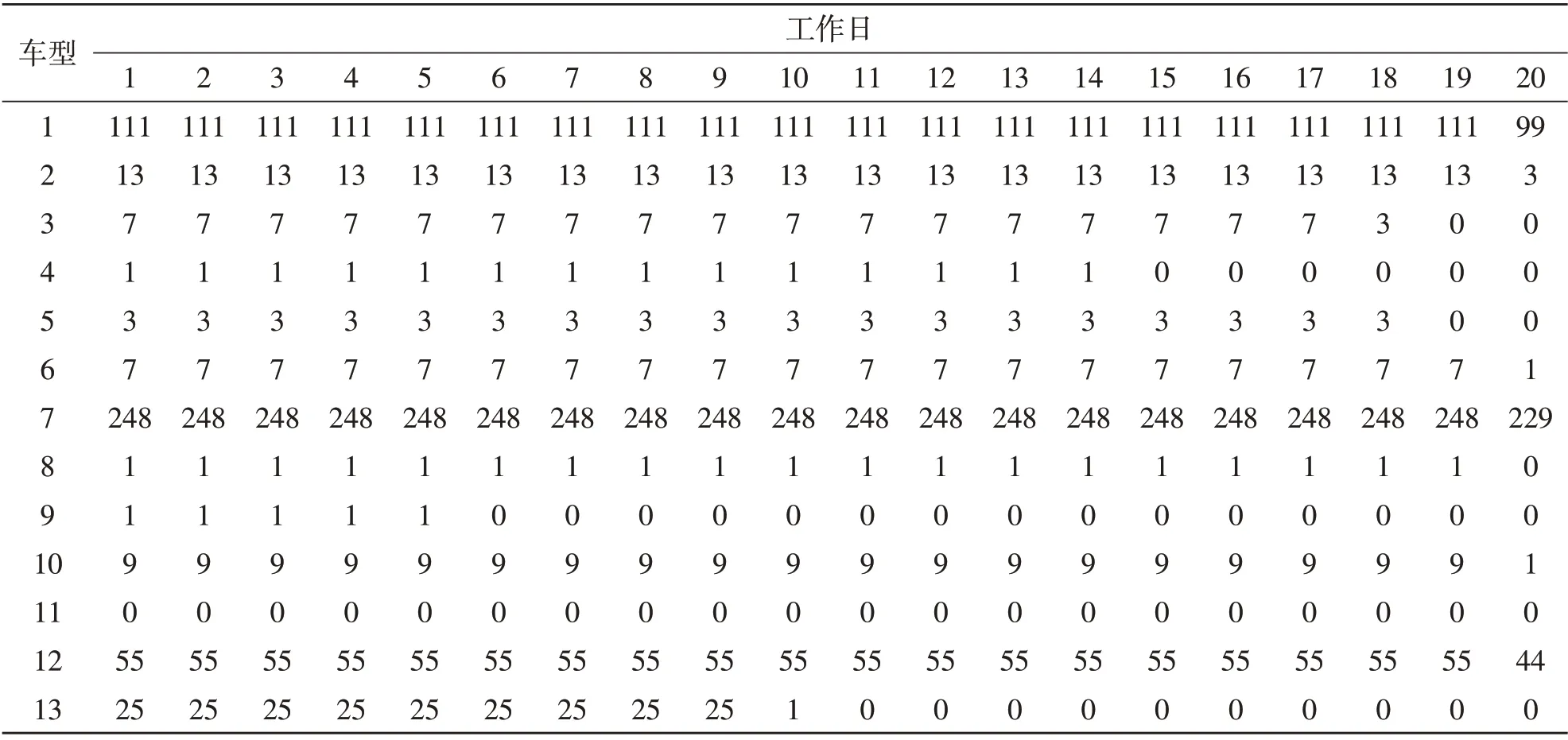
表1 每日作业21 h日排产量 辆

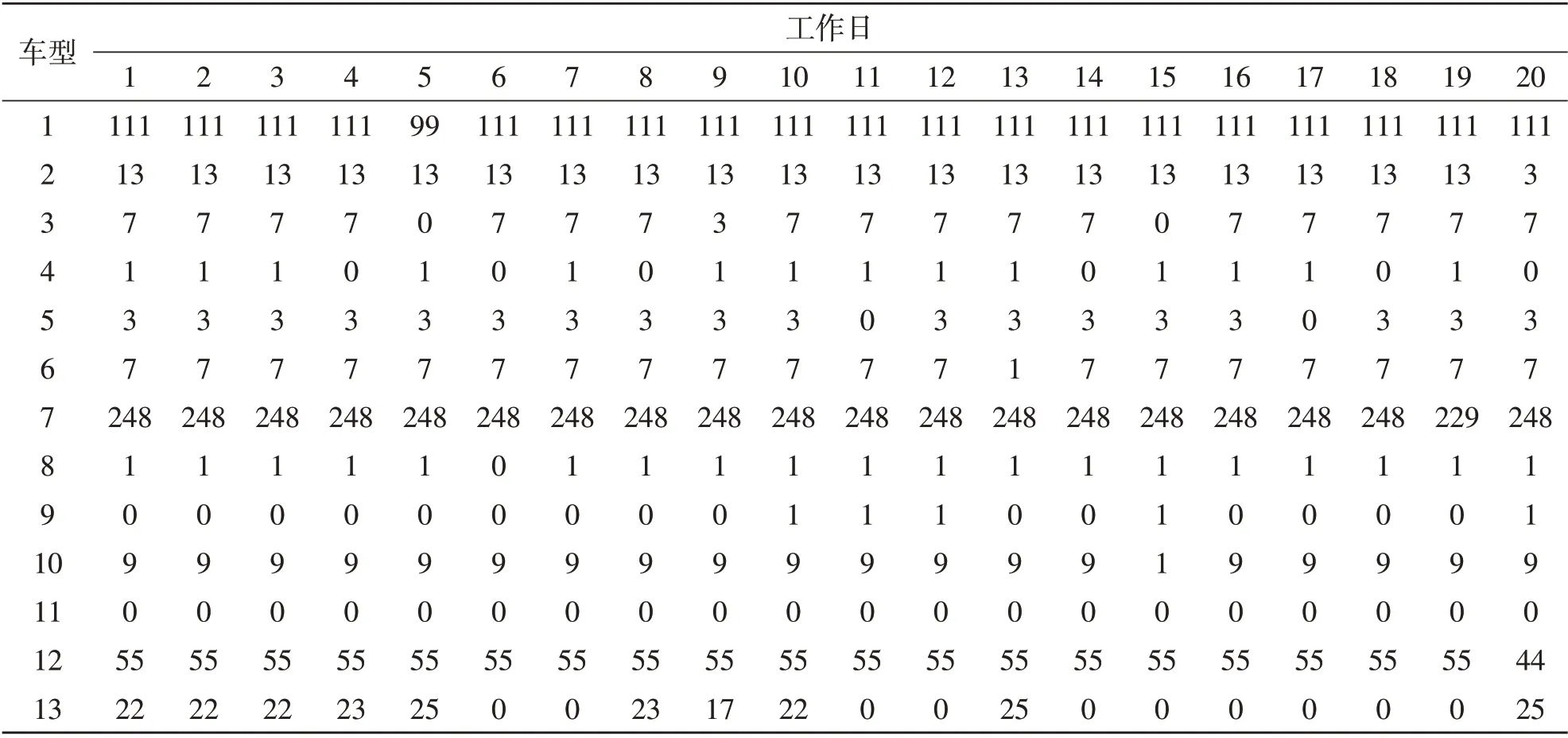
表2 每日作业19.4 h日排产量 辆

3.2 生产任务分配

将某日生产计划代入产线分配模型，2条产线的生产任务分配结果见表3，完工时间见表4。根据程序运行结果，原方案E线工人比F线工人早下班83 min，通过将部分车型7 的生产任务从F 线分配到E线，E线工人比F线工人早下班3 min，2条产线完工时间差距缩减了80 min。

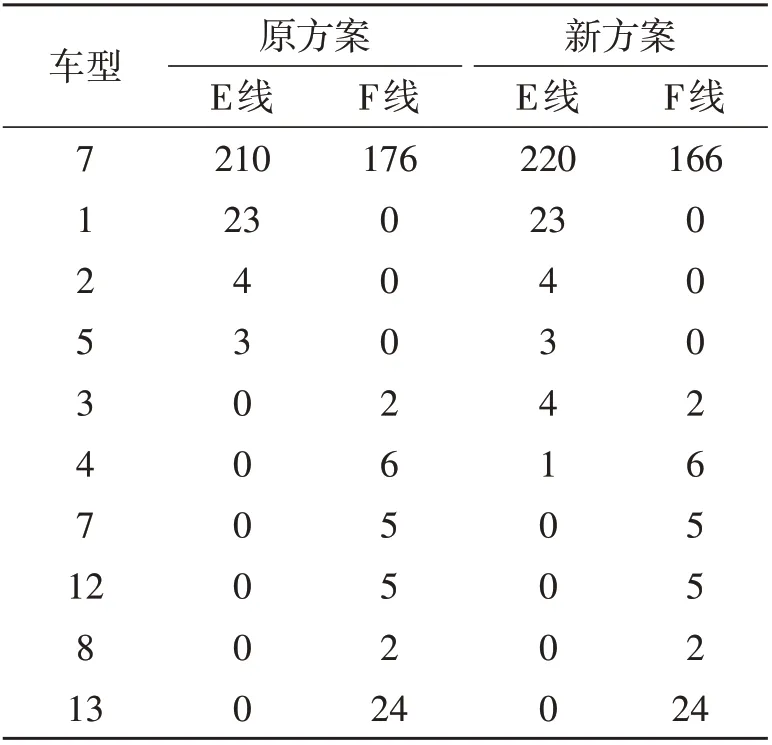
表3 E线和F线排产量 辆

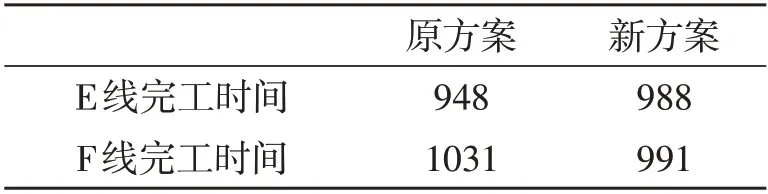
表4 产线完工时间 min

将某日生产计划代入E线班次分配模型，E线白夜班的生产任务分配结果见表5，完工时间见表6。根据程序运行结果，原方案E 线白班工人比夜班工人晚下班2.5 min，通过重新分配各车型白夜班的生产数量后可实现E 线白班工人比夜班工人早下班0.5 min，白夜班作业时间差距缩减了2 min。

表5 E线白夜班排产量 辆

表6 E线白夜班完工时间 min

将某日生产计划代入F线班次分配模型，运行结果见表7，完工时间见表8。根据程序运行结果，原方案F线夜班工人比白班工人晚下班49 min，通过重新分配各车型白夜班的生产数量后可实现F线白班工人和夜班工人同时下班，白夜班作业时间差距缩减了49 min。

表7 F线白夜班排产量 辆

表8 F线白夜班完工时间 min

综上，生产任务分配模型可使产线间、班次间的生产任务分配更加公平、合理，对公司实现公平原则、实施同工同酬制度提供支撑。

3.3 车间作业计划

VNS算法的求解过程如图2所示，邻域变化为2个位置元素的交换操作。系统随机生成1个初始车型序列，记为序列1，自动计算按此顺序生产所用的时间。随机选取2 个位置的车型进行生产顺序互换，生成序列2，用时优于序列1，更新序列为序列2。再随机选取2个位置的车型进行生产顺序互换，生成序列3，由于序列3的生产用时高于序列2，此时序列不更新，仍按序列2进行邻域变化。如此反复，直至到达算法内置的迭代次数，输出最优序列及用时。

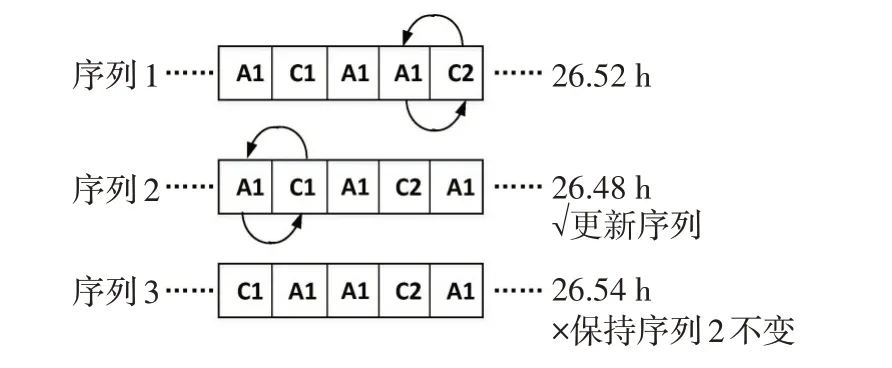
图2 最优解寻找示例

以某日E 线白班生产任务为例，使用VC++6.0运行VNS，按照原排产顺序，完成时间为26.60 h，生产序数为4，算法迭代次数为10 000 次，运行10次，得到10种方案，结果如表9所示。将10种方案与原方案进行比较，找出生产效率最高即完成时间最小的方案，方案3～10均满足条件，方案3和方案4 的序数最少，可减少线上的换型次数，故车间作业计划可参考方案3 和方案4，见表10。根据程序运行结果，重新调整生产顺序后，方案3和方案4单班次完工时间减少0.29 h，为减少生产周期、实现流生产提供了有利的支撑。

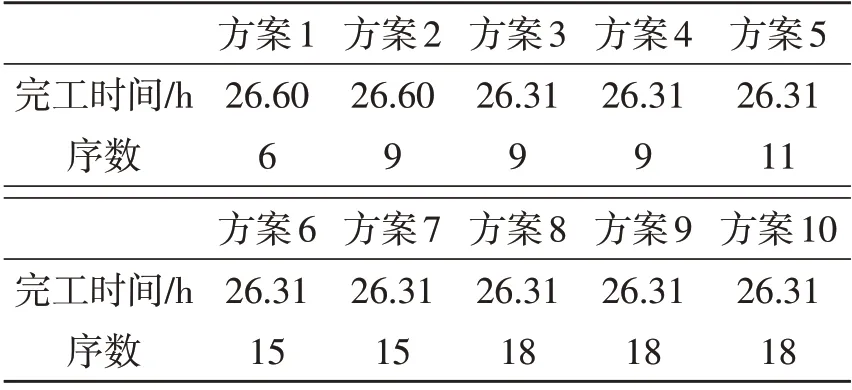
表9 某日E线白班方案

表10 最优车间作业计划

4 结论

以某总装车间生产计划的制定为例，以提高生产效率作为改善点，对生产大纲计划和车间作业计划进行优化。建立了“量利人耗”的数量模型，通过CPLEX求解生产计划，用VNS求解车间作业计划，调整生产顺序，工人生产效率更高，任务分配更加公平。此外，程序采用开源代码进行编写，方便嵌入到其他系统中。