基于不同工况的牵引车车架有限元分析

夏秋阳，尹长城，刘秀琼，王长福

（1.湖北汽车工业学院 汽车工程学院，湖北 十堰 442002；2.襄阳群龙汽车部件股份有限公司，湖北 襄阳 441100）

重型载货汽车的车架不仅要承受发动机、变速器和载货车箱的质量，还要在汽车行驶过程中承受各种力和力矩，车架的可靠性直接影响整车行驶的安全性［1］。国内目前主要通过有限元软件结合实车验证的方法对车架静动态性能进行仿真与优化设计。杨强等结合CAD模型对车架进行有限元建模，建立4 种典型工况对车架强度进行分析，通过有限元软件计算，求得各工况下的静态安全因子和应力分布［2］。丁文敏基于车架有限元模型对其进行了自由模态分析，表明其固有频率处于激励频率范围之外，满足动态性能要求［3］。SUN 等人利用Nastran 计算并显示了5 种工况车架上的危险位置和最大应力位置［4］。文中以某型半挂牵引车为研究对象，为降低成本，采用梁理论模型计算的方法代替实车验证，验证完成后，对车架进行静力学分析和模态分析。

1 有限元模型建立

车架主要材料为WL540 汽车大梁专用钢，其屈服强度高于400 MPa，抗拉强度为540～650 MPa，材料的弹性模量取210 GPa，泊松比为0.3，密度为7850 kg·m-³。车架承受的载荷主要是质量载荷，其中车身总成质量为787 kg、动力总成质量为1434 kg、油箱及燃油质量为350 kg、电池组质量为150 kg和鞍座质量为18 000 kg。

将车架几何模型导入前处理软件HyperMesh，抽取各纵梁和横梁等薄壁构件中面，并采用四节点的壳单元进行离散，板簧支架和发动机支架则采用四面体单元进行离散。为保证单元质量，采用径向网格对车架上存在的众多孔进行划分。车架的纵梁、横梁及其连接板等是通过铆钉和螺栓进行连接的，为模拟此连接，先用RBE2 连接孔周围2 层节点，再用BAR单元连接RBE2。而车架上不同构件之间的接触采用了GAP 单元，能模拟结构两节点间的接触、摩擦和间隙等连接关系［5］。悬架系统的模拟采用了spring 单元，因spring 单元每次只能定义1 个方向的刚度，需要在两节点间分3 次定义3个与坐标轴反向的刚度，且由于板簧水平方向的刚度比垂直方向大得多，水平刚度设定为垂直刚度的100 倍。如图1 所示，弹簧单元垂直方向的刚度计算公式［6］为

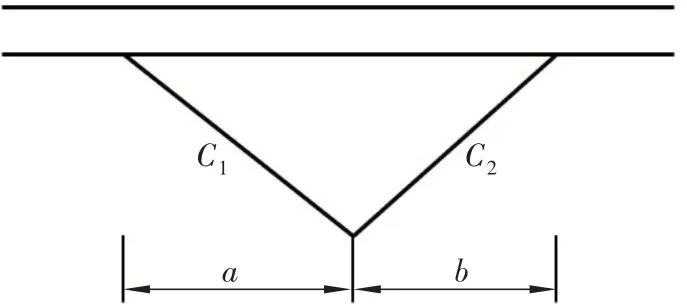
图1 悬架模拟示意图

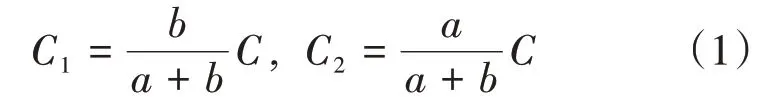
式中：C1、C2为两弹簧单元垂直方向的刚度；C为钢板弹簧刚度；a和b为钢板弹簧两端的长度。根据各板簧刚度，计算得到各弹簧单元垂向刚度，如表1所示。图2为建立的车架有限元模型。

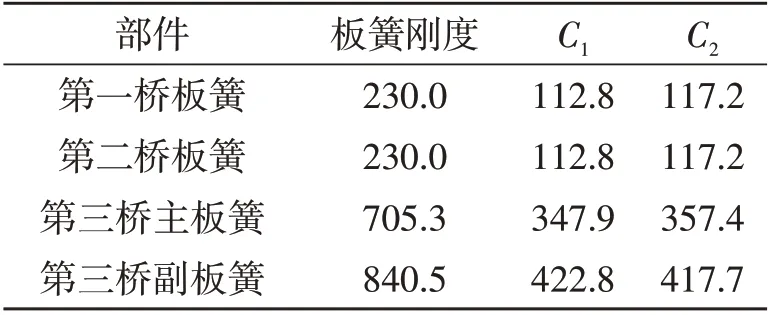
表1 车架板簧刚度特性 N·mm-1

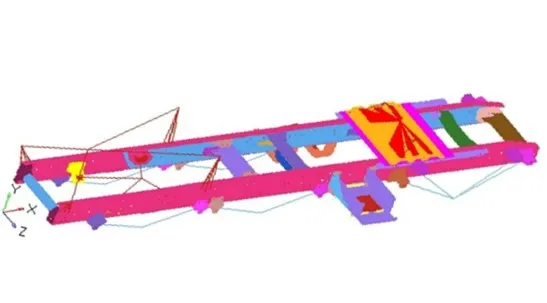
图2 车架有限元模型

2 有限元模型验证

利用材料力学理论计算车架弯曲工况下的最大Mises 应力，与有限元模型计算结果对比，以保证有限元模型在建模、连接、载荷施加等方面的准确性及后续工况分析和模态分析的有效性。

2.1 弯曲工况理论计算

对边梁式车架而言，弯曲工况下作用在车架上的弯曲力矩主要是由车架的纵梁承受。为简化计算，假定1根纵梁承担车架全部载荷的1/2，建立理论计算简化模型如图3所示。图3中2个铰支座分别位于第一、二桥中间处和第三桥处，F1、F2、F3、P分别为车身总成、动力总成、油箱和鞍座各自重力载荷的1/2，换算时重力加速度g取10 m·s-2。

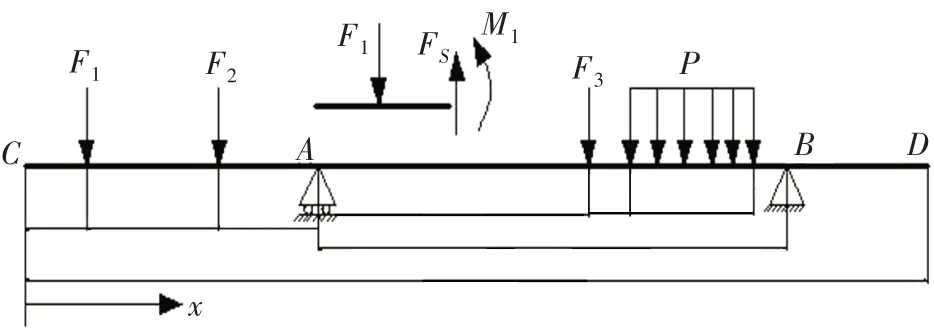
图3 理论计算力学模型

根据模型静平衡状态可计算出车架各段的弯矩大小。由材料力学理论可知，当剪力为零时弯矩会达到极值，计算得该车架弯曲工况的最大弯矩Mmax为4.34×107N·mm。由于车架纵梁为槽型截面零件，车架的最大正应力为

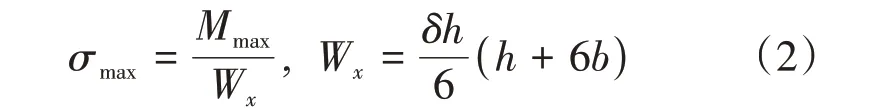
式中：Wx为纵梁对x轴的抗弯截面系数；h、b分别为纵梁高度和宽度；δ为板料厚度；σmax为最大正应力。图4为槽型截面计算简图。经计算得到力σmax为137.8 MPa，材料力学中Mises应力为

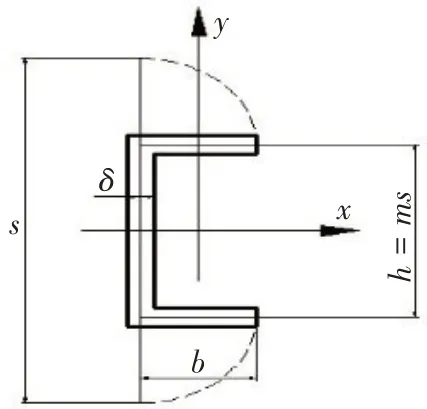
图4 车架槽型截面计算简图

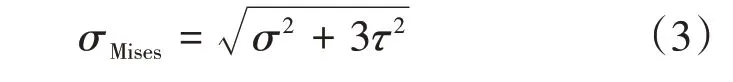
由于该最大应力发生在车架表面处，为平面应力状态，故剪切应力τ可忽略不计，即弯曲工况Mises近似等于最大应力σmax。

2.2 弯曲工况有限元计算

车架处于弯曲工况时所施加的载荷与约束如图5所示。在车架有限元模型上，以集中力和均布力的方式施加主要载荷，约束第一和第三桥处spring单元节点y、z方向的位移自由度，释放x向位移自由度和绕3 个轴的旋转自由度。约束第二桥spring 单元节点x、y、z方向位移自由度，并释放其绕3个轴的旋转自由度。

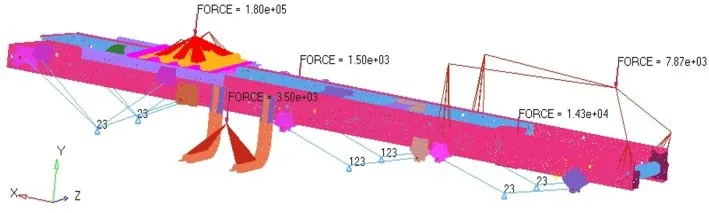
图5 弯曲工况的载荷与约束

有限元计算结果如图6 所示，其最大Mises 应力值为127.9 MPa，与理论计算结果的误差为7.7%，主要为力学模型简化造成，在可接受范围内，说明了有限元建模的正确性。

图6 弯曲工况有限元计算结果

3 典型工况静力分析

在利用车架弯曲工况验证了有限元模型准确性的基础上，对车架扭转工况、制动工况与转弯工况进行有限元分析。

3.1 工况载荷与约束

1）扭转工况 扭转工况为模拟路面不平时车架的响应情况，载荷与弯曲工况保持一致。约束第三桥单元节点x、y、z方向的位移自由度，约束第二桥单元节点和第一桥右侧单元节点y、z的位移自由度，释放各节点其他方向的位移及旋转自由度。

2）制动和转弯工况 制动和转弯工况需用质量点与加速度替换原载荷，如图7 所示，在挂车质心处建立质量为3.81×104kg 的质量点，通过RBE3单元与鞍座连接。制动工况下，需沿模型y负方向施加1g的重力加速度，沿x正方向施加0.3g的水平加速度。约束各桥单元节点x、y、z方向位移自由度，释放所有节点的旋转自由度。转弯工况下，则需沿模型y负方向施加1g的重力加速度，沿z正方向施加1.494 m·s-²的水平加速度。约束第三桥单元节点x、y、z方向位移自由度，约束其余单元节点y、z方向位移自由度，释放所有节点的旋转自由度。

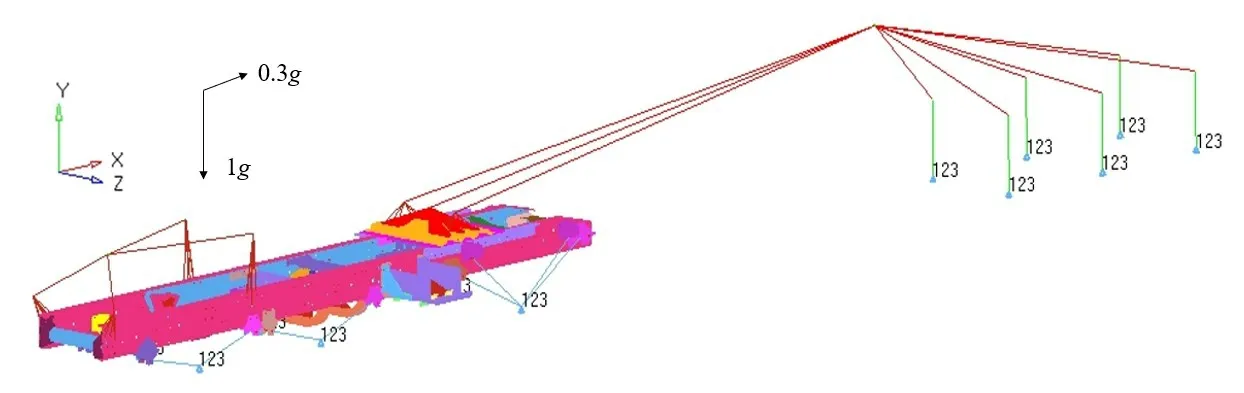
图7 制动工况的载荷与约束

3.2 有限元分析结果及校核

经计算，4 种典型工况下车架的最大Mises 应力与许用应力如表2 所示。结果表明，4 种工况下车架的最大Mises 应力均小于许用应力，车架的强度满足要求。

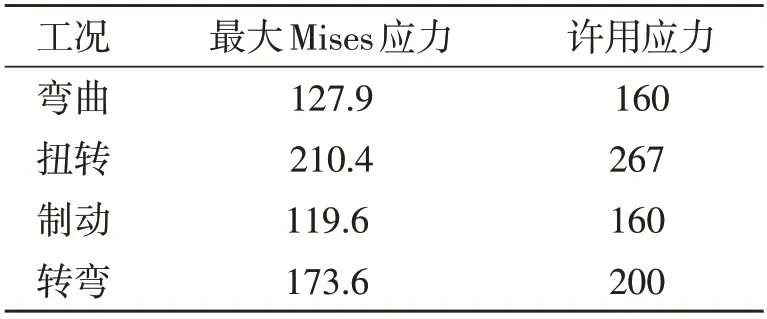
表2 车架最大Mises应力与许用应力 MPa

4 模态分析

车架激励主要来自发动机、路面与车轮不平衡等。路面激励由道路条件决定，在高速公路和一二级公路上路面激励多在3 Hz 以下，因车轮不平衡引起的激励频率一般低于10 Hz。在这些激励共同作用下，车架将呈现扭转振动模态、弯曲振动模态以及弯扭综合振动模态，若车架固有频率与这些激励频率接近，会发生共振，影响车辆舒适性与安全性。高阶固有频率对车架的影响较小，所以更关注低阶固有频率。设计时要求车架1阶扭转和1阶弯曲频率应高于悬架固有频率6～8 Hz，同时低于发动机怠速运转频率［7］。发动机怠速运转频率为

式中：N为发动机转速；Z为发动机的气缸数；τ为发动机的冲程数。已知该车发动机采用6 缸4 冲程，怠速时转速为600 r·min-1，计算得f为30 Hz。

表3为车架模型的模态分析结果，1阶扭转与1阶弯曲频率均大于10 Hz 且小于20 Hz，较好地避开了主要共振区间。此外，由图8 可以看到车架1阶振型为整体扭转，2～3阶振型为车架的水平弯曲和垂直弯曲，也验证了开口薄壁构件扭转刚度小于弯曲刚度的特性。

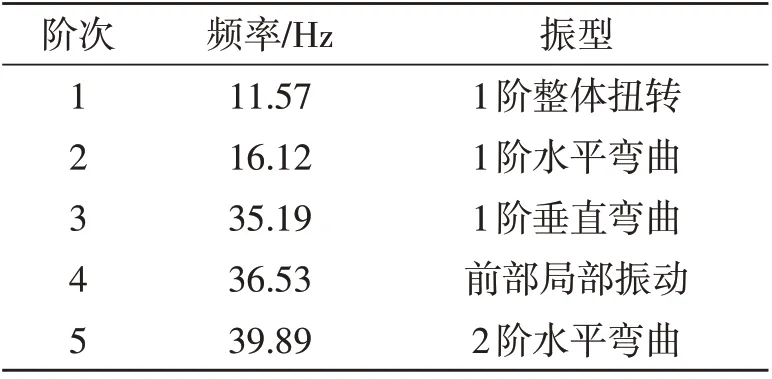
表3 车架前5阶固有频率与振型

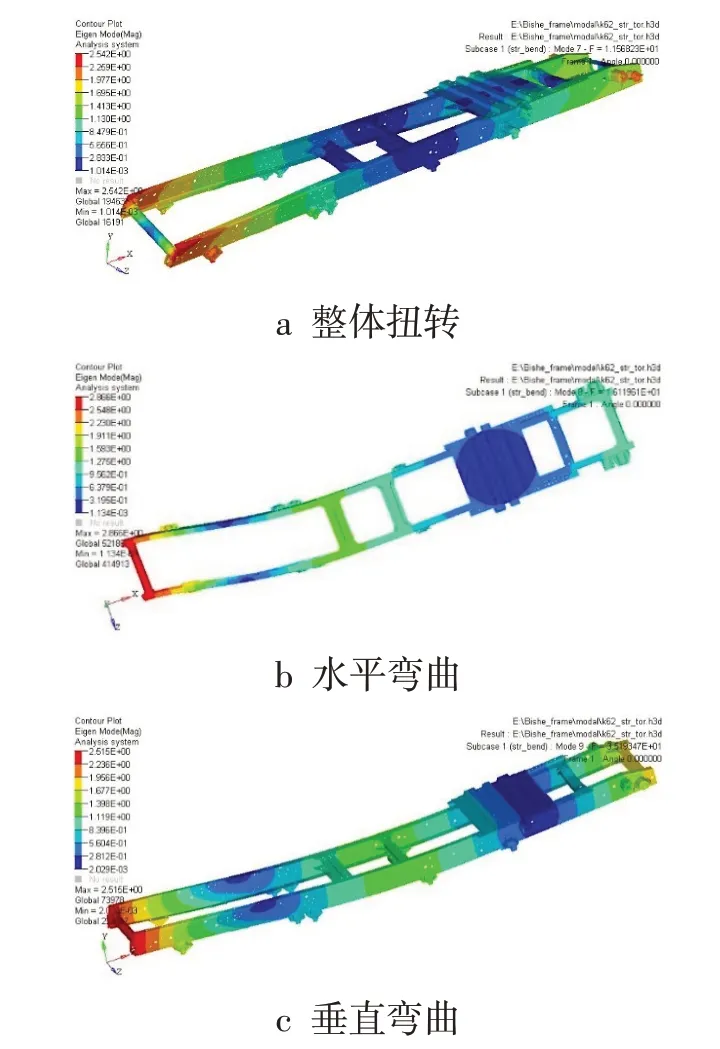
图8 车架前3阶振型

5 结论

使用梁理论计算方法，验证了某型牵引车车架有限元模型的合理性与准确性。对车架4 种典型工况下的强度进行校核，结果显示各工况最大Mises应力均小于材料的许用应力，说明车架强度满足使用要求，为开展车架的疲劳试验设计提供了基础。最后对车架进行模态分析，显示其1阶扭转频率和1 阶弯曲频率避开了车辆发动机和路面所带来的主要激振频率，有效防止了共振的发生。