基于ANSYS的飞机起落架用金属关节轴承静力学分析

赵 凯

(西安航空职业技术学院，陕西 西安 710089)

对于飞机而言，起落架是其起飞与着陆的主要载体，在飞行着陆与滑行中需承受较大冲击载荷。飞机起飞与着陆时，轮胎与地面发生接触，前起落架收放作动筒执行收放动作，而关节轴承受载荷状态实时变化，其主要载荷包括径向与轴向两种。飞机起飞着陆时的侧向力基于主支柱承担，关节轴承运动模式为内外圈转动，摆动角度非常小，关节轴承的轴向载荷并不显著，变化主要体现于径向载荷方面[1]。

段宏瑜，刘红宇，朱琳琳[2]对径向载荷在轴承受力中的影响进行了有限元分析；ZHAO X，FANG C，CHEN Y等人[3]研究分析了径向轴承接头处于不同的载荷条件下时出现的响应失效行为；林志埙[4]对关节轴承径向受载的具体情况进行了有限元分析。目前多数研究都是针对正常位置的轴承加以探究与分析的，而且大部分面向径向载荷，但实际上在具体工况下，相较于外圈，轴承内圈会存在一定程度上倾斜，并且载荷形式也十分繁杂[5]。针对这些既有研究的不完善，本文基于ANSYS进行了飞机起落架用金属关节轴承静力学分析。

1 飞机起落架用关节轴承分析

飞机起落架收放系统中的关节轴承主要形式为杆端关节轴承[6]，具体如图1所示。

图1 杆端关节轴承

飞机起落架收放作动筒具体如图2所示。

图2 前起落架收放作动筒

2 飞机起落架用金属关节轴承结构

选择某飞机起落架用金属关节轴承结构作为实例进行分析，其包含内圈和外圈两部分，而轴承的内外球面彼此相接触，以组成可滑动摩擦副，所用材料为高强度不锈钢。在外圈端面上附带着圆环沟槽的金属关节轴承示意图[7],具体如图3所示。

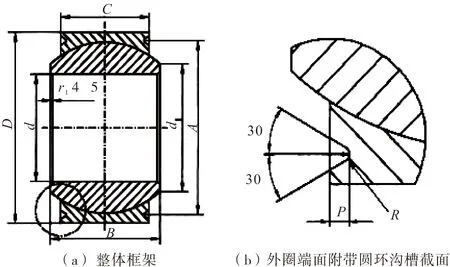
图3 外圈端面附带圆环沟槽的金属关节轴承

外圈端面附带圆环沟槽的金属关节轴承结构参数[8],具体如表1所示，材料参数具体如表2所示。

表1 结构相关参数 mm

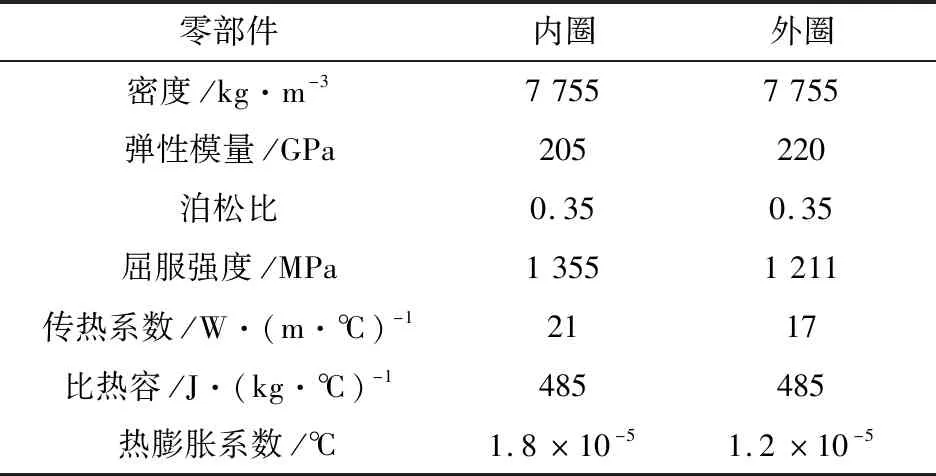
表2 材料相关参数

3 飞机起落架用金属关节轴承静力学分析

3.1 有限元分析模型构建

在静力学分析时添加了碳素钢制成的轴承座，其以扫掠网格进行划分，内圈与外圈分别以六面体网格加以划分，其中端面沟槽应力变化比较明显，需进一步细化网格。金属关节轴承与轴承座有限元模型[9]具体如图4所示。

图4 金属关节轴承与轴承座有限元模型

3.2 载荷与边界条件设定

载荷与边界的条件具体设定为：轴承座的内表面与外圈外表面设定成彼此捆绑、相互接触的状态，以MPC接触算法加以分析。轴承座的内圈外表面与外圈内表面设定成彼此摩擦、相互抵触的形态，通过增强Lagrange算法作为接触算法加以分析。轴承静态极限径向载荷则设定为159.2 kN，轴向载荷设定为29.1 kN，以极限载荷加以分析。以三种不同工况[10]进行详细分析，具体如图5所示。

图5 金属关节轴承载荷与边界条件

工况a：正常位置承担径向载荷，内圈内表面则增加径向载荷，轴承座底部进行固定约束；工况b：正常位置承担双向载荷，内圈内表面添加径向载荷，内圈-圆环端面增加轴向载荷，同样在轴承底座进行固定约束，以局限轴承座端面x向平移自由度；工况c：倾斜位置承担双向载荷，内圈倾斜角为15°，载荷添加与工况b相同，同样于轴承底座进行固定约束，以局限轴承底端面x向平移度。

3.3 分析结果

3.3.1 工况a时静力学分析结果

工况a时金属关节轴承静力学分析结果具体如图6所示。

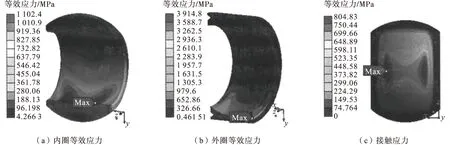
图6 工况a时金属关节轴承静力学分析结果

由图6可以看出，内圈的最大等效应力小于其材料屈服强度，体现于内表面，这主要是由于此表面为径向力受力面；外圈的最大等效应力大于其材料屈服强度，体现于端面沟槽底部，此处应力值明显大于其他处，表明端面沟槽内出现了应力集中的现象，从而引发了外圈的部分材料发生了一定程度上的塑性变形；而接触应力则均匀分布于内圈外表面被挤压处。

3.3.2 工况b时静力学分析结果

工况b时金属关节轴承静力学分析结果具体如图7所示。

图7 工况b时金属关节轴承静力学分析结果

由图7可以看出，内圈的最大等效应力相对于其材料屈服强度略大，微量材料会出现塑性变形；外圈的最大等效应力发生于距离轴向加载侧端比较远的端面沟槽底部；基于双向载荷作用，金属关节轴承最大等效应力与最大接触应力相对于单纯径向载荷作用下的应力较大；接触应力相对偏高的部分逐步迁移于距离轴向较远的加载侧端，最大应力明显大于纯径向载荷作用时的接触应力。

3.3.3 工况c时静力学分析结果

工况c时金属关节轴承静力学分析结果具体如图8所示。

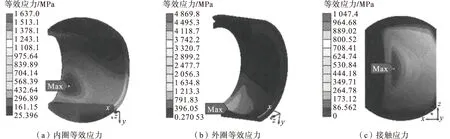
图8 工况c时金属关节轴承静力学分析结果

由图8可以看出，内圈的最大等效应力明显大于其材料屈服强度，只有少量材料会出现塑性变形现象，体现于内表面，接近轴向加载侧端；外圈的最大等效应力发生于距离轴向加载侧端比较接近的端面沟槽底部。

综上所述，受极限载荷作用影响，端面沟槽底部发生了应力集中现象，而且相较于材料自身的屈服强度，外圈的最大等效应力更大，很容易引发塑性变形；受双向载荷作用影响，相较于径向载荷作用下的应力，金属关节轴承的最大等效应力和最大接触应力更大；应避免关节轴承长期处于双向极限载荷作用下运转，避免内圈与外圈发生塑性变形的范围过大，以此引发轴承失效[11]。

4 飞机起落架用金属关节轴承热力耦合分析

受制于热力耦合分析计算量过大，模型须进一步简化，将内圈倒角、外圈端面沟槽、热辐射、其他层面与环境形成的热对流等的影响直接忽视，设定内外圈接触面换热系数为2×104W/m2·℃。

4.1 模型构建

基于ANSYS的瞬态动力学模态开展热力耦合分析，因此在模型中需添加加载板零部件，设定为刚体[12]。

4.2 载荷与边界条件设定

明确设定内圈与外圈的单元属性，具体即热结构耦合单元，以六面体网格划分。以三种不同工况进行分析，工况a为加载板的顶层上添以159.2 kN径向载荷，以约束其在y轴向平移之外的自由度，内圈内表面在x轴向的旋转自由度；工况b则是基于工况a载荷和边界条件，约束除了围绕x轴向旋转与沿着x轴向平移之外的全部自由度，内圈端面添加29.1 kN轴向载荷；工况c为内圈的倾斜角是15°，以工况a载荷与边界条件为前提，约束除了围绕x轴向旋转与沿着x轴向平移之外的全部自由度，内圈端面添加29.1 kN轴向极限载荷。

以7 s为载荷总分析时间，以22 ℃为环境温度。

4.3 结果分析

4.3.1 内圈热力耦合分析结果

在1～7 s时，内圈温度具体如表3所示。

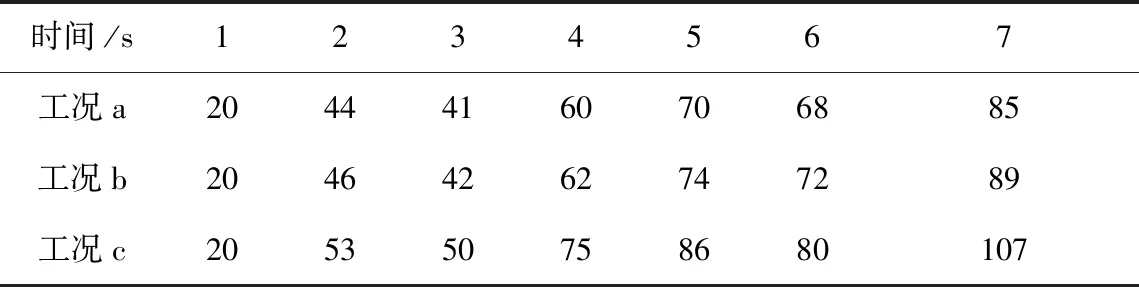
表3 基于不同时间的内圈温度 ℃

由表3可以看出，随着时间变化，内圈温度呈现为在波动状态下逐步上升的趋势，这主要是由于内圈与外圈的相对运动速度始终保持正弦函数关系，如此在速度相对偏小的时候，轴承摩擦生热也会随之减小，再加上摩擦生热相对于轴承导热速度偏慢，因此温度会出现下降现象。

工况a时内外球面接触中心位置的温度最高，工况b时最高温度的范围开始逐步转移到距离轴向加载侧端较远的方向，这主要是因为轴向力导致此范围区域承载了过大的双向载荷，在双向载荷作用下内圈的温升较快，工况c时内圈高温范围与内圈外圈接触面边界相靠近，表面内圈倾斜角为15°时，温升明显大于非倾斜位置时的金属关节轴承。

4.3.2 外圈热力耦合分析结果

在1～7 s时，外圈温度具体如表4所示。

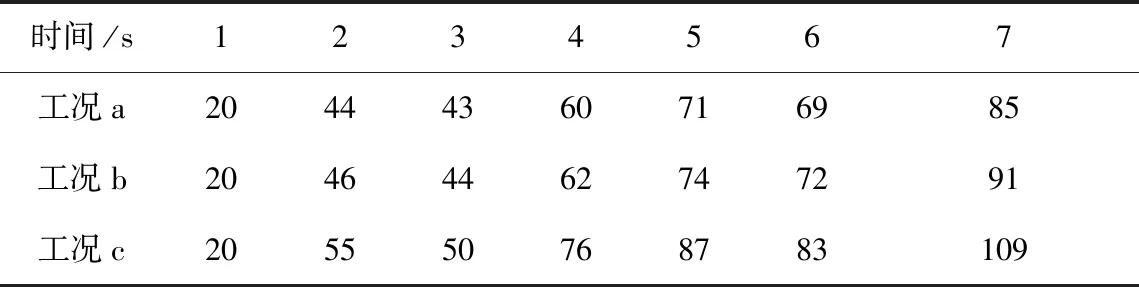
表4 基于不同时间的外圈温度 ℃

由表4可以看出，随着时间变化，外圈温度呈现为在波动状态下逐步上升的趋势；三种不同工况下，外圈最高温度都相对大于内圈最高温度。

综上所述，基于极限载荷作用时金属关节轴承启动时会摩擦生热，但是在双向载荷作用时摩擦温升速度相较于单径向载荷作用时的温升速度更快，且保持于倾斜位置状态时摩擦温升更为显著；应避免关节轴承长期处于极限载荷或者倾斜位置下运转，避免过高温升，以造成轴承性能弱化，导致胶合失效[10]。

5 结 论

综上所述，本文基于ANSYS进行了飞机起落架用金属关节轴承静力学分析与热力耦合分析，结果表明，受极限载荷作用影响，端面沟槽底部发生了应力集中现象，而且相较于材料自身的屈服强度，外圈的最大等效应力更大，很容易引发塑性变形；受双向载荷作用影响，相较于径向载荷作用下的应力，金属关节轴承的最大等效应力和最大接触应力更大；应避免关节轴承长期处于双向极限载荷作用下运转，避免内圈与外圈发生塑性变形的范围过大，以此引发轴承失效；基于极限载荷作用时金属关节轴承启动时会摩擦生热，但是在双向载荷作用时摩擦温升速度相较于单径向载荷作用时的温升速度更快，且保持于倾斜位置状态时摩擦温升更为显著；应避免关节轴承长期处于极限载荷或者倾斜位置下运转，避免过高温升导致轴承的使用性能变差，进而造成胶合失效；可科学规划润滑结构，以改善润滑性，缩小摩擦因数，减小轴承摩擦生热。