纤维混凝土断裂性能的研究现状及展望*
魏新江 任梦博 冯 鹏 吴 熙 廖 娟
(1.浙江大学建筑工程学院,杭州 310058;2.浙大城市学院工程学院,杭州 310015;3.清华大学土木工程系,土木工程安全与耐久性教育部重点实验室,北京 100084)
传统的混凝土是由水泥、粗细骨料、水和外加剂等材料复合而成的[1]。在目前的大多数结构中,混凝土被用作最主要的建筑材料[2]。经工程实践和试验证明,混凝土的抗压强度以及耐腐蚀性能较好,但其抗拉强度较差,大约为抗压强度的1/10,存在准脆性破坏的现象[2-4]。即使在钢筋混凝土中,满足工程应用变形需求的条件下,也难免存在细微的裂缝。混凝土或内部钢筋发挥的桥接应力对裂缝的发展限制能力有限,增加了工程风险和修补成本。随着新型建筑材料的发展,混凝土中加入的纤维能够克服混凝土的缺陷,改善其抗裂性能和力学性能。在特定的工程领域,纤维混凝土正逐渐代替钢筋混凝土和预应力混凝土,其抵抗裂缝发展的机理以及评定纤维混凝土断裂性能的方法正在受到更多学者的关注。
自从Kaplan在1961年用Griffith理论研究混凝土的断裂特性以来[5],随着断裂力学理论研究在混凝土领域的应用与发展,断裂力学模型和断裂参数理论的发展正在推动纤维混凝土理论与应用不断创新与成熟。纤维混凝土与素混凝土存在一定的断裂性能差异,断裂曲线也有所不同,表现最明显的就是断裂试验曲线的峰值后阶段,所以混凝土断裂力学的理论需要加以改进来适应纤维混凝土与普通混凝土的差异。纤维混凝土的纤维混合方式繁多,纤维在混凝土中的位置分布和取向不易控制,不同纤维混凝土试件开裂后断裂性能也相差较大,这些都是纤维混凝土的研究难点,也是开展纤维混凝土断裂参数研究的主要原因。
通过对现有测定纤维混凝土断裂参数的断裂试验进行整合,分析其特点,综合现有的技术标准和纤维混凝土相关文献中的断裂参数计算方法,同时结合纤维混凝土断裂参数研究文献对其进行横向比较,提出各断裂参数的使用建议以及不足点。此外,通过对文献的整理和现有研究结果的分析,梳理影响纤维混凝土断裂参数的因素,并结合文献数据分析给出各影响因素对纤维混凝土断裂参数的影响规律。
1 纤维混凝土断裂试验
基于断裂力学的理论知识来研究纤维混凝土的断裂性能,需要合理描述其断裂性能的参数。断裂参数的计算需要通过对纤维混凝土试件进行断裂试验来获取试验数据,因此断裂试验的设计和选用与断裂参数的准确性密不可分。断裂试验实质上是通过对试验试件的加载来研究试件中裂纹的发展速度及最终破坏规律。
目前国内外对纤维混凝土的断裂试验,大多为带缺口的三点弯曲断裂试验和带或不带缺口的四点弯曲断裂试验,试验装置上主要为加载方式的不同,如图1所示。通过在长方体试件上表面进行中心加载或两点加载,在下表面进行两点支承的方式,用线性可变差动变压位移传感器(LVDT)和夹式引伸计分别测定试件跨中位移(δ)和裂缝口张开位移(δCMOD)。试验大多采用位移控制加载速率,适时观测试件表面裂缝的发展速度和扩展形态。三点弯曲和四点弯曲试验可以观测加载过程中的裂缝扩展模式,还可得到荷载-跨中挠度关系(P-δ)、荷载-裂缝口张开位移关系(P-δCMOD)和荷载-裂缝尖端张开位移关系(P-δCTOD)等试验曲线。
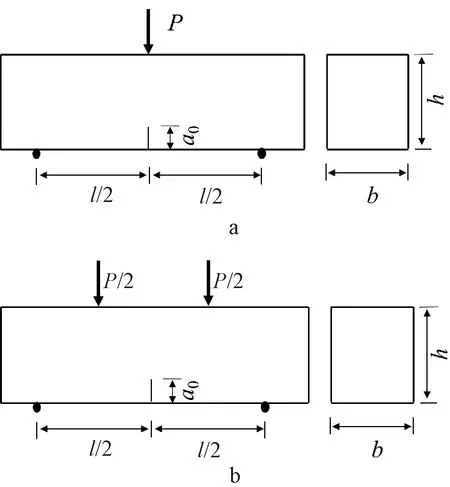
a—三点弯曲试验示意;b—四点弯曲试验示意。图1 纤维混凝土弯曲断裂试验示意(带切口)Fig.1 The schematic diagram of bending fracture tests for notched fiber concrete specimens
弯曲断裂试验目前被大多学者采用,通过断裂试验测定纤维混凝土的断裂性能。因为弯曲试验中试件形状简单、易制作,试验原理和操作简单,试验结果能较好地反映试件的弯曲断裂过程。但三点弯曲断裂试验、四点弯曲韧性试验的试件下表面是两支点支承,导致试件的自重荷载会对试件结果产生影响,且随试件尺寸增大,影响明显加大[6-7]。为了消除弯曲试件对纤维混凝土断裂参数测量的影响,文献[8-9]介绍了对三点弯曲梁试验装置的改进,提出结构重力不做功的试验方法。无重力影响的弯曲试验的原理为:根据力学计算的方法,合理延长弯曲试件两支点外伸出的长度,使得跨中断裂区的弯矩降低为零,从而抵消试件重力对断裂试验的影响。
因为加载方式的不同,三点弯曲梁和四点弯曲梁的断裂区域的受力状态具有显著区别。文献[10-12]介绍了采用相同尺寸试件的三点和四点弯曲试验的区别。在相同钢纤维掺量的情况下,纤维混凝土试件在四点弯曲试验中有更大的抗弯强度和峰值荷载。除此之外,与三点弯曲断裂试验相比,四点弯曲断裂试验试件两加载点范围内无剪切应力,弯矩无变化。三点弯曲试件跨中受最大弯矩和剪力的共同作用,且断裂区受施加荷载的楔形扩散影响更明显。
在纤维混凝土断裂参数的测定中,带切口试件在三点弯曲试验中更为常见。试件切口是人为设置试件加载下裂缝开始的位置,切口位置处应力集中现象明显。对比相同试件的断裂试验,有切口试件断裂参数小于无切口试件的,且带切口试件裂缝集中出现在切口上方[12]。由于四点弯曲试验中试件断裂区弯矩相同,受加载压力楔形分布的影响较小,裂缝分布更均匀,故四点弯曲试验可更好测定纤维混凝土的强度等断裂性能指标。
除了弯曲试件被用于测量纤维混凝土的断裂参数外,劈拉试件也可被用于纤维混凝土的断裂性能测量试验中。文献[13-14]对比分析了纤维混凝土试件在单轴荷载和双轴荷载作用下的楔入劈拉试验结果,发现单、双轴荷载下的楔入劈拉试件均能较好地测量其耗能能力。Raja等通过楔入劈拉试验研究了粗骨料粒径对钢纤维混凝土断裂性能的影响,得到试件的断裂能随粗骨料粒径增大而增大的结论[15]。Abrishambaf等通过劈拉试件对比了纤维方向对断裂性能的影响规律,发现垂直切口方向的纤维可明显提高试件的残余强度[16-17]。Löfgren等应用楔入劈拉和三点弯曲梁试验,分析了纤维尺寸对纤维混凝土试件断裂能的影响,结果显示,与三点弯曲试验的结果相比,楔入劈拉试验的结果离散程度小,楔入劈拉法适合纤维混凝土断裂参数的测定[18]。所以,劈拉试件可以用来测量纤维混凝土的断裂性能,可通过劈拉试验的荷载-裂缝口张开位移曲线,较好地反映试件开裂前后的断裂性能[19]。
2 纤维混凝土的断裂参数
随着纤维混凝土在机场人行道[20]、地铁管片[21-22]等应用范畴的不断增加,基于断裂力学研究纤维混凝土的断裂性能,从而挑选合理的断裂参数可指导纤维混凝土构件的优化设计。
2.1 纤维混凝土断裂参数
评估纤维混凝土的断裂性能和力学性能是优化纤维混凝土构件的关键,涉及到断裂试验标准、试验曲线处理方法等。参考大量文献以及技术标准,总结出现采用频率较高的技术标准:RILEM TC 162-TDF[23]、UNI 11039-1[24]、ASTM C1609[25]、EN 14651[26]等,这些技术标准主要评价的是纤维混凝土开裂后,纤维对混凝土裂缝扩展的限制作用以及断裂性能的提高程度。目前使用的纤维混凝土断裂参数主要有等效抗弯强度、断裂韧度、残余强度、弯曲韧性指数、断裂能。
2.1.1等效抗弯强度
在目前纤维混凝土断裂特性研究文献中,主要以弯曲断裂试验为主,在断裂参数选择中更多偏向于等效抗弯强度,因为等效抗弯强度建立了吸收的断裂能与强度之间的联系,明确了试验曲线不同区间内纤维对纤维混凝土断裂性能的提高幅度。等效抗弯强度的计算涉及试验曲线上计算点区域内的吸收能量,不因试验曲线计算点突然增大或减小而使得试件的抗弯强度突变。
在UNI 11039-1[24]中,介绍了描述钢纤维混凝土开裂后断裂性能的断裂参数,主要包括:第一开裂荷载(P1f) 、第一裂缝强度(f1f)、等效强度(feq(0-0.6),feq(0.6-3)),计算式如为:
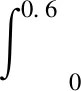
(1a)

(1b)
(1c)
(1d)
式中:U1、U2分别为试验曲线相应区段的下围面积;l为试件的跨度;b和h分别为试件的宽度和高度;a0为试件的切口深度。
RILEM TC 162-TDF[23]中同样采用了曲线特定区域下围面积换算弯矩来计算等效抗弯强度。选用的下围面积直接排除了比例极限荷载点位移(δL)区域内的面积,更加突出了钢纤维对混凝土的增强作用,但等效弯曲强度的准确性与δL的选取有关。等效抗弯强度计算表达式为:
(2)

根据邓宗才提出的评价混杂纤维混凝土弯曲韧性的等效抗弯强度[27],可由测得带切口的三点弯曲断裂试验的P-δ曲线推出。其特点是将素混凝土峰值荷载对应的挠度值视为纤维混凝土的初裂挠度值(δult,p)。为便于分析纤维混凝土中纤维对试件断裂韧性的提高作用,采用不同挠度处的等效抗弯强度(σeq(n))研究其断裂性能,计算式如下:
(3)
式中:Epc为P-δ曲线上特征挠度下面积与初裂挠度下面积之差;n为所选取的初裂挠度的倍数。
2.1.2断裂韧度
断裂力学中,断裂韧度为试件失稳破坏时的应力强度因子临界值[28]。断裂韧度的计算式与断裂模型有关,主要采用式(4b)计算的断裂韧度KIC[28]。
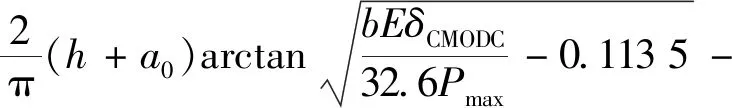
a0
(4a)
(4b)
(4c)
(4d)
(4e)
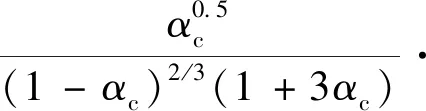
(4f)
其中ah=(t+a0)/(h+t);αc=ac/h
式中:δCMODC为峰值荷载对应的裂缝张口位移;Ci为初始柔度,从P-δCMOD曲线的初始直线段得到;β为跨高比;Pmax为峰值荷载;s为试件的跨度。
2.1.3残余强度
EN 14651[26]提出残余强度的概念来评价纤维混凝土开裂后的性能,即用P-δCMOD曲线上特定点的残余抗弯强度(fR,j)来描述纤维混凝土峰值后的断裂性能,表达式如下:
(5)
式中:PR,j为P-δCMOD曲线特定点的荷载值,j=1,2,3,4。
2.1.4弯曲韧性指数
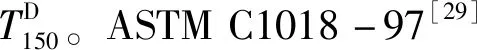
2.1.5断裂能
断裂能GF为裂缝扩展单位面积所需的能量。断裂能与纤维混凝土裂缝扩展吸收的能量成正比。根据三点弯曲切口梁的P-δ曲线,采用国际结构与材料研究所联合会(RILEM)标准测试方法[30],计算式如式(6):
(6)
式中:W0、m分别为三点弯曲梁的断裂功和两支点间的质量;δ0为试件破坏时的挠度;g为重力加速度;Alig为跨中韧带面积。
2.2 断裂参数特点分析
从设计的角度来评估纤维混凝土的断裂参数是非常重要的。在计算断裂参数时,主要通过直接处理试验获得的P-δCMOD、P-δ等曲线得到初裂荷载、最大荷载、峰值荷载后特征时刻所对应的曲线面积或面积比来描述纤维混凝土的耗能能力,或者通过特征点的荷载直接计算弯曲强度,或采用曲线面积间接换算的弯曲强度来评估纤维混凝土的韧性、强度等指标。
国际上关于评价纤维混凝土断裂性能的标准计算方法有两种:1)从试验曲线的某一点荷载值或强度来判断,如初裂荷载、峰值荷载、残余强度等;2)试验曲线一定区域内的面积或面积换算值,如峰后区域等特征时刻所对应的曲线面积或面积比、残余强度、等效抗弯强度等。在现有的断裂参数中,可大致将其分为两大类:第一类参数是计算过程中涉及P-δ或P-δCMOD曲线所围面积或积分,反映试件耗能能力或韧性的相应参数,包括等效抗弯强度、弯曲韧性指数、断裂能等。第二类是计算试验曲线上特征点的强度或断裂韧度等断裂参数,不涉及曲线积分类的参数,如残余强度、断裂韧度等。
以上介绍的两大类参数各有特点。第一类曲线积分或特定区域内的曲线所围面积都涉及到试件破坏吸收的断裂能概念,与第二类的显著区别为:前者试验曲线上的前后点计算参数可为包含关系,如曲线横坐标的大区间包围面积包含横坐标较小区间的包围面积;第二类不涉及积分或面积类的断裂参数,前后特征点的关联较小,通常为曲线范围内δCMOD为0.5,1.5,2.5,3.5 mm对应点的抗弯强度,联系若干残余强度值来判断试件的断裂性能。
第一类断裂参数中的弯曲韧性指数和等效抗弯强度相似,均以面积直接和间接换算的方法来描述纤维混凝土的韧性。ASTM C1018中,计算不同区间曲线下围面积比得出的弯曲韧性指数I5、I10、I20,反映了纤维混凝土与理想弹塑性材料的偏离程度,也可以体现出纤维材料种类、体积率、形状和长径比对混凝土弯曲韧性的提高幅度[31]。I5、I10、I20需要准确测定初裂点的位置,但初裂点的选取易受试验条件和人为因素的影响,精确程度不能保证。故文献[27,32]提出的等效抗弯强度,以素混凝土的峰值变形作为纤维混凝土的初裂点计算等效弯曲强度,避免初裂点的选取精确度对断裂参数带来的影响。
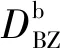
在对待纤维混凝土试件开裂前吸收的断裂能时,与RILEM TC 162-TDEF不同,UNI 11039-1中定义的等效抗弯强度并不排除这部分的断裂能。Caggiano等使用UNI 11039-1的feq(0-0.6)、feq(0.6-3)评价掺加不同长径比纤维后的纤维混凝土的断裂性能[4],feq(0-0.6)、feq(0.6-3)计算中包含素混凝土吸收的断裂能。Barros等研究了钢纤维混凝土的开裂后性能,应用RILEM TC 162-TDF的等效弯曲强度feq,j和残余强度fR,j描述钢纤维混凝土的开裂后断裂性能,feq,j可更好表达纤维对混凝土开裂后断裂性能的提高程度[33]。此外发现:feq,j与fR,j之间具有较强的关联性,但fR,j表现出更大的离散度。与等效抗弯强度、断裂韧度等相比,残余强度计算简便,且易于评估,但也更容易受到试验过程中记录的曲线的不规则性的影响,计算结果离散度较大。此外,等效抗弯强度和残余强度均假设试件横截面应力按直线分布,这忽视了裂缝扩散、断裂过程区对纤维混凝土试件横截面应力分布的影响。
断裂能和断裂韧度与抗弯强度的计算角度不同,断裂能和断裂韧度分别表征纤维混凝土试件整体破坏所吸收的单位能量和裂缝尖端临界应力因子,体现了纤维和混凝土基体共同作用对试件断裂性能的提高程度。Ghasemi等同时采用断裂能和断裂韧度处理试验曲线,在评价不同粗骨料掺量对照组断裂性能时,局部出现相异的断裂参数起伏规律,说明在评价纤维混凝土断裂性能时,不同参数混合使用更能论证尺寸效应等规律[34-35]。Alberti计算了曲线挠度分别为1,5,8 mm时混合纤维混凝土的断裂能,发现分段区间的断裂能可更好地反映纤维混凝土不同受力阶段的断裂性能[36]。
整体来说,多种类型纤维混合得到的混凝土性能更为优异,纤维混凝土领域的研究领域也转向混合纤维混凝土,但是混合纤维混凝土的断裂过程更为复杂,试验曲线的形状也更为多样,为评价其断裂性能,应通过研究加载过程中不同加载阶段的断裂参数,综合评价混合纤维混凝土试件开裂过程中不同受力阶段的断裂性能。通过对前面断裂参数特点进行的分析对比发现:等效抗弯强度更能适应不同的试验曲线,将吸收断裂破坏能转化为抗弯强度,突破了传统的强度和断裂能计算方法。此外,等效抗拉强度能分加载阶段来评价纤维混凝土的断裂性能,故在国内外纤维混凝土文献中的研究更多。目前,国内外对断裂参数的研究仍在不断完善。
3 断裂参数影响因素
综合国内外学者对纤维混凝土断裂参数的研究结果可以发现,影响纤维混凝土断裂参数的因素错综复杂。可将影响纤维混凝土断裂参数的因素归为以下层面:纤维层面、混凝土基体层面和断裂试验方法层面。
3.1 纤维对纤维混凝土断裂参数的影响
针对纤维混凝土的断裂性能,目前国内外的研究重点在纤维方面。纤维作为增强混凝土力学性能和断裂性能的辅助材料,不同组合方式对其断裂性能起着重要的调节作用。综合现有研究文献可知,纤维对纤维混凝土断裂性能影响因素可分为4类:1)纤维掺加量;2)纤维混合方式;3)纤维方向和位置;4)纤维长径比。
纤维的混合方式、长径比和掺加量等同时影响纤维与混凝土的黏聚力、纤维间距,改变纤维混凝土的加载断裂速度和开裂程度。结合近年来纤维混凝土断裂性能研究文献,表1列出了部分研究结果。
表1表明:纤维混凝土的断裂性能并不随纤维掺量而单一变化,要达到最优的断裂性能存在最佳纤维掺加量;对于掺加不同种类纤维的纤维混凝土,断裂能和断裂韧度等参数随掺加纤维体积率的变化规律不同,最佳掺加纤维量和最优纤维组合方式也不同;结合不同纤维混合方式的纤维混凝土断裂性能研究结果,刚度较大的纤维与柔度较大的纤维混合,峰值荷载前后显现出较好的断裂性能,且断裂性能的改善可与纤维混凝土裂缝出现后的拉拔效应建立联系,纤维的拉拔效应与外部作用激活的纤维特性、数量、激活纤维与加载方向的倾角有关,同时也会改变裂缝的扩展速度[37-38]。此外,定向分布的纤维能显著增强纤维混凝土的断裂性能,同时具有小长径比的纤维能增大纤维混凝土的断裂韧度和等效抗弯强度。

表1 纤维混凝土断裂参数部分试验结果Table 1 Experimental results of the fracture parameters of fiber reinforced concrete
3.2 混凝土基体对纤维混凝土断裂参数的影响
纤维混凝土中的纤维主要依靠与混凝土基体的黏结来共同承担断裂荷载,跨越裂缝两端的纤维可以桥接裂缝,依靠自身的抗拉性能来继续传递应力,使裂缝两端的混凝土继续吸收断裂能,减缓混凝土抗拉区域材料抗拉能力的缩减速度。纤维混凝土开裂后的断裂性能主要依靠荷载激活的纤维,但混凝土在纤维混凝土开裂后的加载过程中,依然会对断裂参数产生影响。
Xu等研究了钢纤维混凝土的断裂性能与粗骨料直径和掺加量之间的联系[54]。钢纤维混凝土的GF和KIC均随最大骨料尺寸和粗骨料掺加量而线性增加,粗骨料尺寸和掺加量的增大也会线性增长纤维混凝土试件断裂过程区的有效长度。增加的原因可能是粗骨料能延长裂缝扩展的路径,但只限定于一定的粗骨料体积率内。Beygi等研究表明纤维混凝土的断裂能随粗骨料的尺寸和掺加量而增加,描述脆性的特征长度也线性增加[55]。Alyhya等发现断裂能随粗骨料的掺量增加[56]。Ghasemi等调查了3种不同骨料尺寸的钢纤维混凝土,发现断裂能随之波动[35]。Ochi等研究发现聚对苯二甲酸乙二醇酯纤维混凝土的断裂韧性随水灰比的增大而减小[57]。Beygi等在保证最大骨料粒径不变的前提下,断裂能会随水灰比的减小而增大[55]。Lee等研究了不同混凝土强度(C25、C35、C45)对钢纤维混凝土梁的残余强度的影响,发现C45的纤维混凝土梁在混凝土开裂后,残余抗弯强度立即快速增大,在一定数量的裂缝出现前,吸收的断裂能增长速度最大[58]。
综上所述,纤维混凝土的断裂参数会随混凝土基体变量波动变化,并有明显规律。如断裂能和断裂韧度会随骨料尺寸和掺加量增加而线性增大,也会由于水灰比的减小而增大等。
3.3 断裂试验对纤维混凝土断裂参数的影响
断裂试验中的试验加载方式、试件尺寸、试件浇筑方法和纤维加入顺序等会对纤维混凝土参数的测定产生影响。素混凝土的尺寸效应等研究已得到大量数据支撑,纤维混凝土由于纤维的掺入,会改变浇模时纤维混凝土的流动性,影响纤维在混凝土中的分布,造成断裂参数具有一定的变化幅度。这也是不同断裂试验无法通过断裂参数进行横向对比断裂性能的主要原因。
纤维混凝土断裂试验中采用的中心加载、四点加载的试件断裂区的受力状态不同,其中无切口的四点弯曲梁试验得到的断裂区裂缝分布更加均匀,得到相应的断裂参数要大于三点弯曲试件。Bencardino等用不同标准研究钢纤维混凝土的开裂后断裂性能,保证相同试件尺寸和相同钢纤维体积率,得出的四点弯曲试验曲线在三点弯曲试验曲线上方,即四点弯曲试验的等效抗弯强度大于三点弯曲试验[10]。
纤维混凝土的试件尺寸对于断裂参数的影响被国内外学者所研究,证明存在尺寸效应,断裂能、韧性的增长与试件尺寸成反比。Sun等研究了不同玄武岩纤维体积率下,玄武岩纤维混凝土的断裂能、断裂韧度与试件横截面面积(A)的变化关系[39],如图2所示。可见:随着试件横截面面积的增大,部分玄武岩纤维体积率的试件的临界断裂韧度与断裂能减小。整体来说,玄武岩纤维对混凝土断裂韧度的贡献与试件横截面面积成反比。Nguyen等研究了形状相同、尺寸不同的钢纤维混凝土试件,试件包含不同体积率混合的粗、细钢纤维[59],四点弯曲试验结果显示试件的断裂性能存在明显的尺寸效应,表现为:随着试件尺寸的减小,等效抗弯强度、韧性明显增大。Kim等对不同尺寸的试件进行了四点弯曲试验,证明存在尺寸效应,随着试件截面减小,试件的断裂能增加[60]。

a—GF与横截面面积A的关系;b—KIC与A的关系。BP-0%;BP-0.1%;BP-0.2%;BP-0.3%;BP-0.4%;BP-0.5%。图2 试件尺寸对玄武岩纤维混凝土断裂参数的影响Fig.2 Influence of specimen sizes on fracture parameters of basalt fibers reinforced concrete
纤维混凝土断裂试验的试样浇筑方法也会改变断裂参数,浇筑位置发生变化会改变纤维混凝土试样中纤维的分布方向和间距。Yoo等研究纤维混凝土浇筑方法对其弯曲性能的影响,发现试模中心浇筑的峰值荷载和峰值后延性会优于端部浇筑试件[61]。Kang等对比了端部浇筑和多点浇筑混凝土的方式,显示前者能将纤维方向效应系数提高到0.6~0.7,从而大幅度提高初裂强度、弯曲抗拉强度、弯曲韧性[62]。另外,纤维在混凝土中的加入先后顺序也会对纤维混凝土的断裂性能产生影响。侯敏等的研究结果表明:玄武岩纤维混凝土在拌制过程中,纤维会吸收部分用于水泥水化的水,影响最终的强度[63]。这反映了纤维混凝土的原料加入顺序会影响混凝土的抗弯强度。
纤维混凝土的断裂参数影响因素与混凝土的相比,增加了纤维对其产生的断裂性能改变,包括纤维掺加量、混合方式、纤维方向等因素。另外,纤维的加入也会和混凝土断裂性能的其他影响变量产生杂糅效应,如纤维会间接影响骨料在纤维混凝土中的均匀分布,也会影响水灰比,改变纤维混凝土的断裂过程区长度。通过合理改变纤维混凝土的影响因素可以提高其断裂性能,优化纤维混凝土。同时纤维加入顺序等影响变量也是断裂试验中要避免的试验干扰因素,应严格控制变量对试验带来的影响。
4 结束语
通过对目前常用的三点、四点弯曲断裂试验方法的总结,分析了各自的特点。综合国内外评价纤维混凝土断裂性能的相关文献和标准,选择目前常用的纤维混凝土断裂参数的计算式和断裂性能评价方法,对其进行了详细介绍。针对上述介绍的断裂参数,结合参数特点,将其分为两类:试验曲线所围面积类断裂参数和不涉及曲线面积类断裂参数。同时分析总结了断裂参数之间的区别和各自的特点以及适用性。参照国内外纤维混凝土研究文献,总结了纤维混凝土断裂参数的主要影响因素。在纤维混凝土影响因素分类的基础上,提出了上述因素对纤维混凝土断裂参数的影响规律。通过总结国内外纤维混凝土断裂参数的研究现状,对纤维混凝土的断裂参数的未来优化研究提出了若干展望。
1)建议优先使用弯曲断裂试验中的四点弯曲试验。相对于三点弯曲断裂试验,四点弯曲试验加载试件的中心断裂区弯矩无变化,断裂区主要存在于试件两加载点中间位置,减少了加载部位压力楔形分布对断裂参数带来的不确定性影响。
2)评价纤维混凝土的断裂性能,选用的断裂参数应突出试件在不同受力阶段,纤维对混凝土断裂性能的改善幅度,建议使用等效抗弯强度评价混合纤维混凝土不同受力阶段的断裂性能,等效抗弯强度可更好地兼顾试件吸收能量和强度之间的联系。另外,断裂性能的评价除了等效抗弯强度等参数外,试件断裂区裂缝的宽度和数目也可作为辅助方法。
3)纤维混凝土的断裂参数影响因素可作为其断裂性能的优化切入点,合理利用纤维混凝土的影响因素可以提高其断裂性能。但在断裂试验中,要严格控制纤维混合方式等影响变量,减小影响变量对试验结果的干扰程度。
4)评价纤维混凝土的断裂性能的断裂试验中,统一试验操作流程(纤维加入顺序、浇筑方法等),且断裂参数应突出纤维对混凝土开裂韧性、抗弯强度的提高增益比。区别于素混凝土,纤维混凝土断裂参数影响因素的纤维层面尚需继续完善和拓展研究,包括纤维混凝土的纤维混合方式和纤维方向。
综合来讲,纤维混凝土由于其抗弯强度及韧性的优良性,在现代工程中的应用领域正在快速扩展。随着断裂力学理论知识的不断发展和成熟,纤维混凝土的断裂参数也在不断创新和完善,断裂参数准确度也在不断提高。合理的断裂参数对于评价纤维混凝土的断裂性能是必要的,有助于优化纤维混凝土的构件,促进纤维混凝土在实际工程的应用,解决现有工程上构件使用周期内提前开裂等问题。

