一种连杆滑槽式手部康复外骨骼的设计与研究

王陈瑁，杨志鸿，汪 涛，管小荣

(南京理工大学 机械工程学院，江苏 南京 210094)

近年来脑卒中病人的数量逐年增长，且该疾病对患者的人身健康和生活有很大危害，约70%的脑卒中存活者会出现不同程度的肢体功能障碍[1]，其中手功能受损会给患者的生活带来不便。传统康复治疗手段的主要依据是康复医疗学中让患肢的持续性被动运动(CPM)理论[2]，但因医师训练效率较低，人力成本较高，并没有得到广泛的普及。

手功能康复训练外骨骼属于康复机器人的一种。近年来，机器人辅助康复逐渐成为医疗界和学术界的一大研究热点[3]。手功能康复训练外骨骼能代替传统康复医师，结合先进外骨骼技术和康复理论，科学地帮助患者进行康复训练，降低康复成本，同时能够减少对医师资源的占用，具有十分广阔的发展前景。Ueki等研制的基于虚拟现实技术的手部康复机器人，具有18个自由度，可以通过数据手套进行双边康复训练[4]。德国Otto Bock公司研制的WaveFlex Hand CPM外骨骼康复手，采用一个电机作驱动，多用于训练四指，也可单独训练拇指。Leonardis等研制的BRAVO采用腱侧手表面肌电信号控制外骨骼运动，具有很多优点，但其缺点是控制不够精确[5]。法国Kinetec公司研制的8091型便携手部康复器,需要性能较高的伺服电机驱动，市场价格较高。北京航空航天大学研制的一款由钢丝绳-绳套传动的外骨骼康复手指机器人[6]，伸缩性较差，容易出现滑动，造成误差的累计[7]。杨岩江研制的手功能康复外骨骼，具有电机驱动和健侧驱动两种形式，且只使用一个直线电机进行五指驱动[8]。张勤超研制的手部功能康复机器人的关节部分采用齿轮齿条平行滑动机构[9]。李朋认为，国外的手功能康复机器人更成熟一些，但价格高昂，而国内在这方面目前还处于起步阶段，没法做到批量生产[10]。

从国内外研究现状看，目前的手功能康复外骨骼大多价格较高、结构复杂、较沉重、不易携带，因驱动少而存在训练动作单一的缺陷。本文将结合市场需求，依据轻量化、低成本化、训练动作多样化等原则，在结构设计、驱动设计和控制系统设计中，进行静力学、正逆运动学分析与仿真，并进行样机实验验证，设计一种欠驱动连杆滑槽外骨骼，用于帮助患者进行持续被动运动性手部康复训练。

1 外骨骼结构设计

人的手部结构如图1所示。人的手指共有下列18个自由度：前端四指每个手指有4个自由度，其中掌指关节(MCP)具有2个轴线垂直相交的转动自由度，近端指间关节(PIP)和远端指间关节(DIP)各有1个自由度；大拇指在指间关节(IP)以及掌指关节各有1个自由度。

图1 人的手部结构

人手一般情况下只能完成两种运动，即弯曲/伸展(简称曲伸)运动和内收/外展(简称收展)运动。能实现弯曲/伸展运动的主关节有指间关节和掌指关节，而能完成内收/外展运动的主要是掌指关节。受人体手部骨骼、韧带肌肉、肌腱等组织的结构限制，手指关节的运动不能在全范围内进行，各关节之间也存在一些约束，手的各MCP之间存在关联。比如，无名指的MCP弯曲的时候，中指与小指的MCP也会出现一定程度的弯曲。MCP的曲伸运动和收展运动之间也存在特定的约束关系，当MCP弯曲的时候其侧向外展运动的幅度会减小。

根据以上人手运动机制，设计外骨骼时，其机械结构应能带动拇指的MCP、四指的MCP和PIP，且应为每根手指配备一部直线电机作驱动，以实现较为理想和丰富的康复训练动作。

1.1 设计分析

本文设计的手部康复外骨骼整体结构如图2所示。该外骨骼由手背部支撑板、拇指训练模块、四指训练模块和直线电机组成。它通过直线电机驱动。5个直线电机分别通过定位销与手背部支撑板固定在一起，其中1个直线电机通过鱼眼杆端轴承与拇指训练模块相连，另外4个直线电机通过鱼眼杆端轴承与四指训练模块相连。

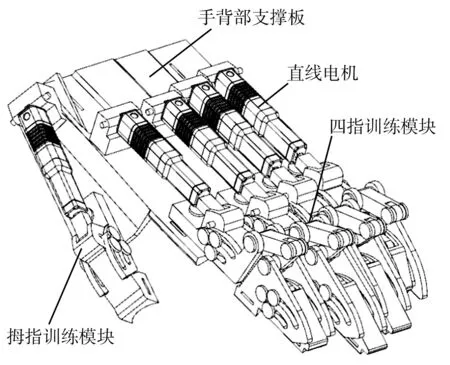
图2 本文设计的手部康复外骨骼整体结构

拇指训练模块与四指训练模块的结构类似。这里以四指训练模块为例进行分析。四指训练模块(图3)由固定在手背板上的第一滑槽、上连杆、中间连杆、下连杆、第一指节套兼第二滑槽、第二指节套组成。由于在各手指运动时，两个近端指间关节之间存在约束关系，因此在机构设计时应采用欠驱动结构，用直线电机推动第一指节套兼第二滑槽在第一滑槽中按固定轨迹运动，使中间连杆在上连杆的限制下绕第一指节套兼第二滑槽与中间连杆的铰接点逆时针转动，从而推动下连杆，使下连杆推动第二指节套在第二滑槽中按固定轨迹运动，带动第一指节和第二指节运动。此外，两个圆弧滑槽的圆心应与手指关节部位重合，使训练机构不会与手指产生相对滑移，以避免患者手部不适。

图3 四指训练模块

拇指训练机构主要带动拇指掌指关节的转动。

1.2 自由度分析

从四指训练模块的机构运动简图(图4)可看出，机构中活动构件数n=7,低副数量PL=10，高副数量PH=0。由此可计算机构的自由度数量F，即

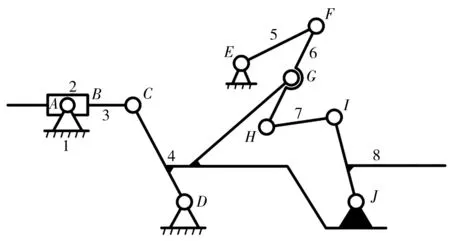
图4 四指训练模块的机构运动简图

F=3n-2PL-PH=1

(1)

由自由度计算可知，主动件数量等于机构自由度数量。因此，机构能够进行确定轨迹的运动。

1.3 力学分析

四指训练模块的4套训练机构结构相同。这里以食指训练机构为例进行分析。食指训练机构的力学解析如图5所示。

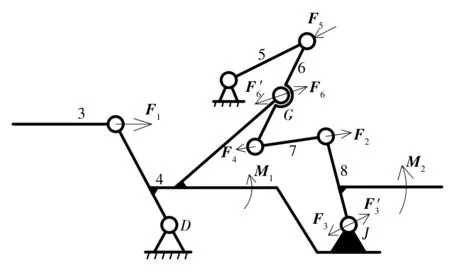
图5 食指训练机构的力学解析

图5中，M1、M2分别为MCP、PIP能产生的抵抗转矩。根据设计惯例，M1、M2可分别取值0.8 N·m、0.4 N·m。

先后对J点、杆件8、杆件7、G点、杆件6、杆件4和D点进行受力分析，可得:

(2)

式中：L2为F2对J点的力臂;L4,L5分别为F4，F5对G点的力臂;L6′,L1,L3′分别为F6′，F1，F3′对D点的力臂。表1所示为各力臂的取值。通过计算，可得表2所示力学分析结果。

表1 各力臂的取值 mm

表2 力学分析结果 N

分析可知，驱动力需要大于F1(其值为67.0 N)。

可根据计算结果进行驱动选型。常用的驱动类型有液压驱动、气动驱动、电机驱动。气动驱动有结构简单、方便维护的优点，缺点是难以精确控制。液压驱动能产生很大推力、体积小，但可靠性差、维修不方便。电机驱动精度高、易于维护，且输出的力或力矩足够带动手部康复外骨骼之需，因此，本文选用电机驱动。

2 外骨骼运动学分析

2.1 已知电机行程后求关节转动角度

手部康复外骨骼能带动手指MCP和PIP的旋转。设MCP的旋转角度为α，PIP的旋转角度为β。

2.1.1 求解MCP旋转角度α

由图4可知，在机架1、摇块2、杆件3、杆件4组成的摇块机构中，若α为杆件4绕D点转动的角度，则该摇块机构可简化为△ACD(图6)。

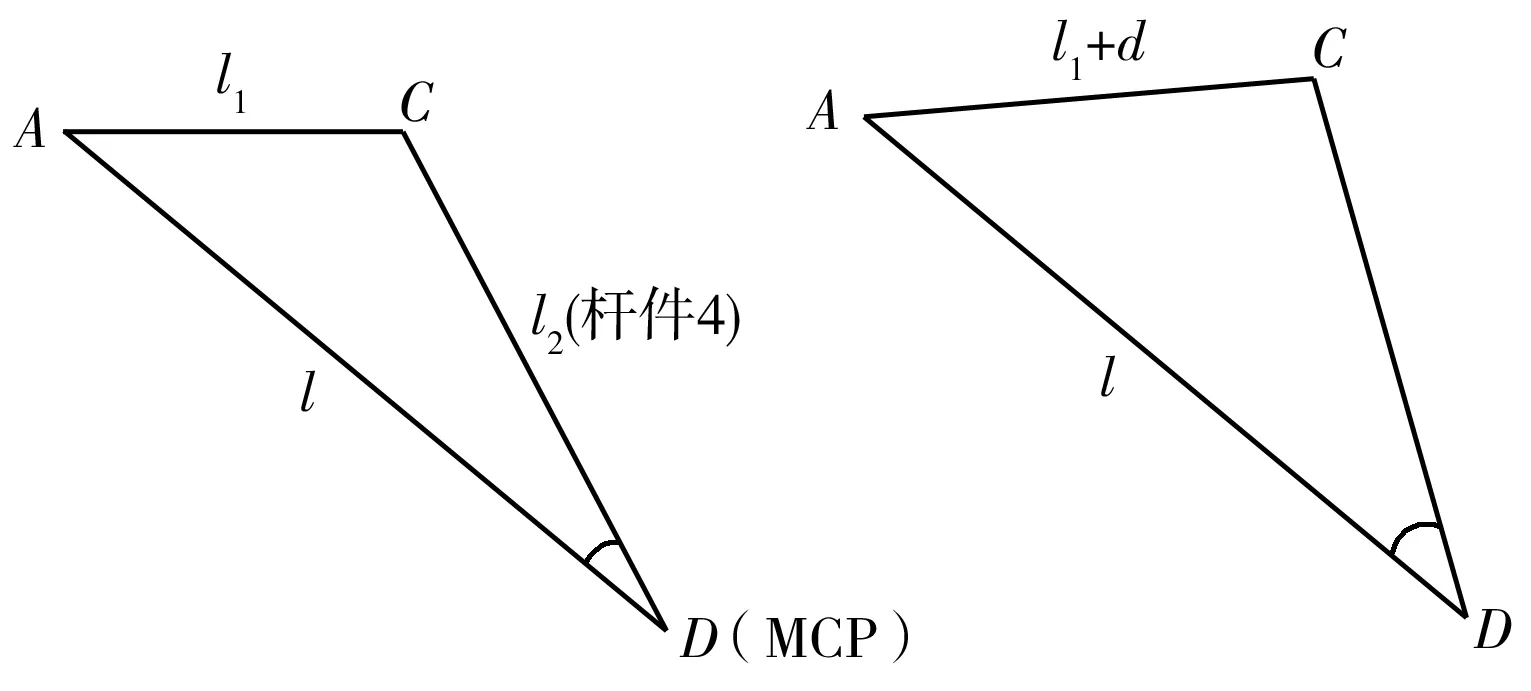
(a) 电机转动前 (b) 电机转动后图6 由摇块机构简化的△ACD

图6中，α可表示为△ACD中∠ADC的变化量。设AC原长为l1，电机转动后AC的伸长量为d，AD的长度为l，CD的长度为l2，则根据余弦公式可得：

(3)

2.1.2 求解PIP旋转角度β

从图4中取出四边形EDGF，建立图7所示的四连杆EDGF结构，以D点到E点方向作为x轴正方向，设DE，DG，EF，FG的长度分别为l3，l4，l5，l6，且初始时，DG，GF与x轴的夹角分别为θ1，θ2，EF与x轴的夹角为θ3。根据机构运动，可设DG与x轴的夹角增大α时，GF与x轴的夹角减小φ。

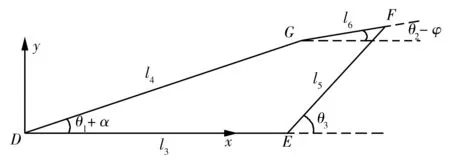
图7 四连杆EDGF结构

对闭环DEFGD应用闭环矢量法，可得：

(4)

消去θ3后假定式(4)的等号两边已归一化，则推导可得：

(5)

根据图4可建立图8所示的四连杆GHIJ结构。

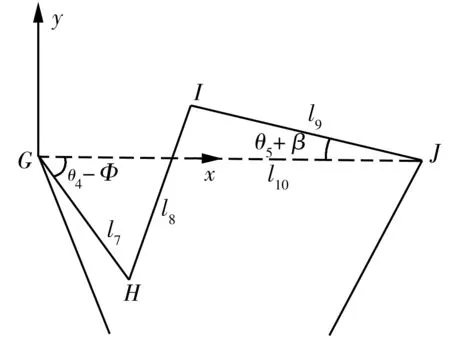
图8 四连杆GHIJ结构

令Φ=α+φ，并以G点到J点方向作为x轴正方向，设GH，HI，IJ，GJ的长度分别为l7，l8，l9，l10，且初始时，GH，IJ与x轴的夹角分别为θ4，θ5。根据机构运动，可设GH与x轴的夹角减小Φ时，IJ与x轴的夹角增大β。

根据几何关系可列出下列式子：

(xH-xI)2+(yH-yI)2=HI2

(6)

对闭环GHIJG应用闭环矢量法，并假定等式(6)两边已归一化，则推导可得：

(7)

2.2 已知关节转动角度后求电机行程

根据图6，在△ACD上建立图9所示含直角坐标系xDy的摇块机构，并设初始时DA与x轴的夹角为θ6。随着机构运动，DA与x轴的夹角会变为θ6+α。

图9 含直角坐标系xDy的摇块机构

根据几何关系，可列出下列式子：

(xA-xC)2+(yA-yC)2=AC2

(8)

通过一定的代入、推导过程,可得出关于α的运动学方程，即

(9)

假定式(8)的等号两边已归一化，则通过一定的代入、推导过程可得：

(10)

根据式(4)和Φ=α+φ，消去θ5后假定等式两边已归一化，则推导可得：

(11)

根据式(9)-式(11)，可推导出关于β的运动学方程，即

(12)

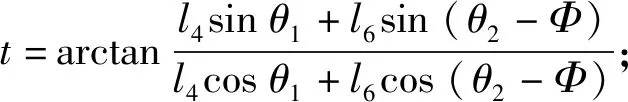
3 仿真及实验验证

3.1 运动学仿真

首先用UG软件建模，然后将模型导入Adams软件，并将直线电机运动速度设定为10 mm/s，仿真时间设定为1.6 s，可进行运动学仿真。外骨骼的运动学仿真结果如图10所示。

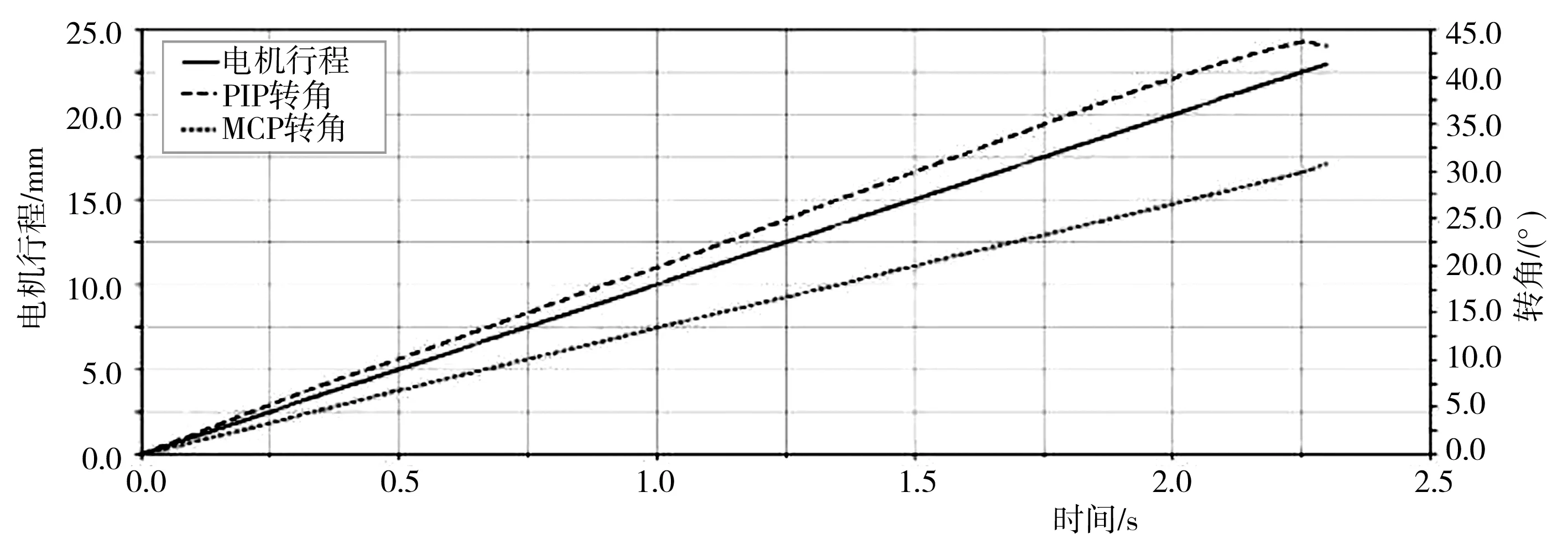
图10 外骨骼的运动学仿真结果

运动学仿真得到的各手指关节活动范围如表3所示。

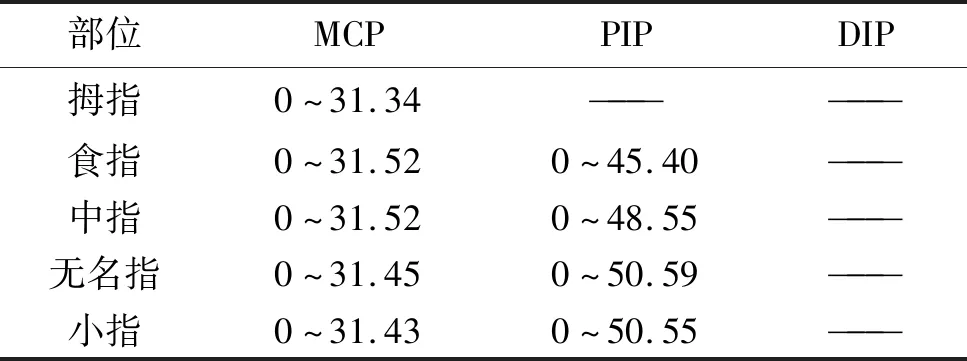
表3 运动学仿真得到的各手指关节活动范围 (°)

通过运动学仿真可知，该手部康复外骨骼可使患者手部在正常范围内运动，具有一定的训练效果。

3.2 机电联合仿真

这里的机电联合仿真是用Adams软件做动力学仿真的基础上，在Matlab中添加开环控制模型，进行仿真，从一定程度上反映实物样机的工作情况，为实物样机的可靠工作提供数据支持。本文以食指MCP为例，通过机电联合仿真，得到了食指MCP的角位移-时间曲线(图11)和角速度-时间曲线(图12)。

图11 食指MCP的角位移-时间曲线

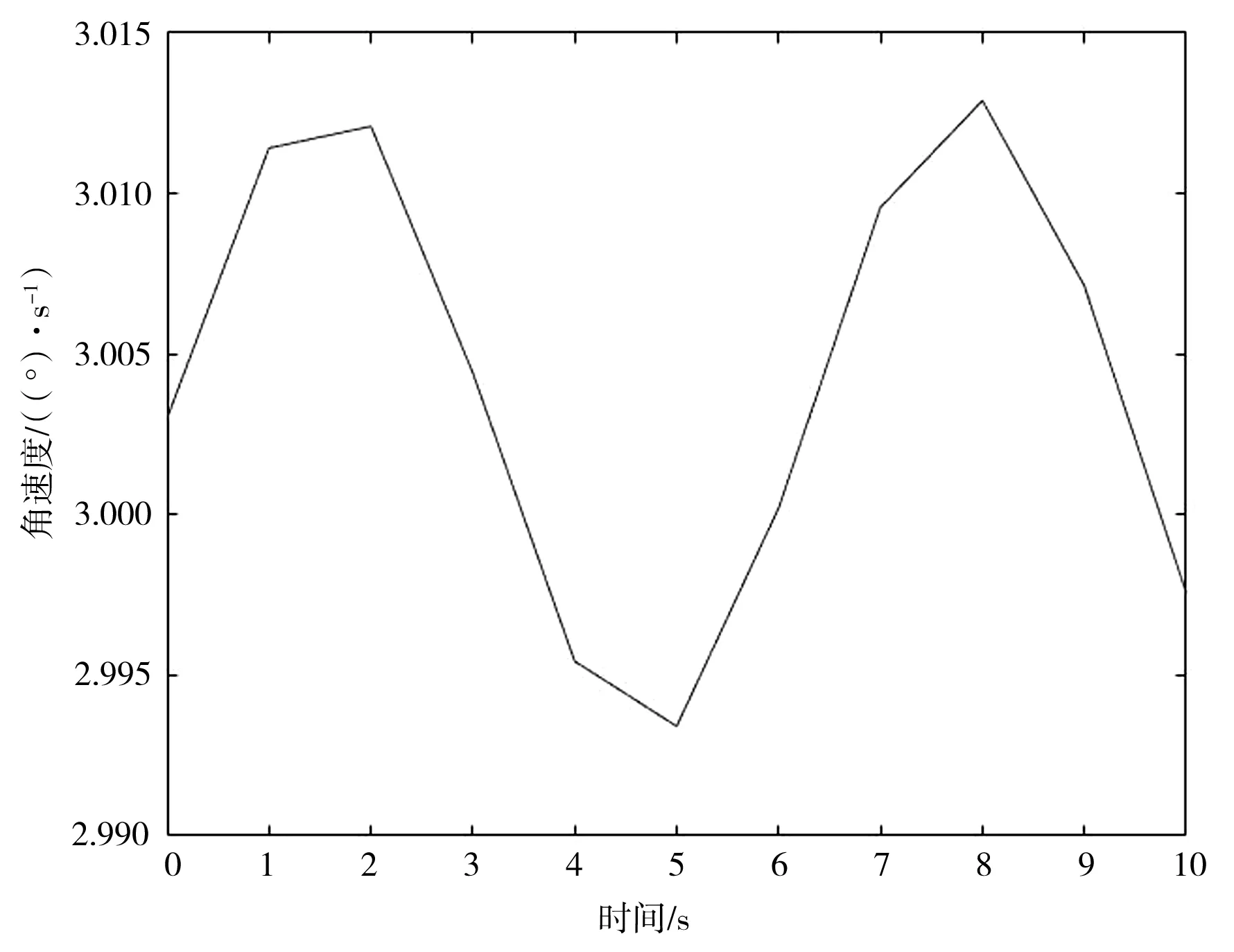
图12 食指MCP的角速度-时间曲线

从图11和图12可看出，食指MCP角位移—时间曲线的线性度较好，而且角速度虽然有一定的波动，但是每秒的波动范围不超过0.05°。由此可见，该手部康复外骨骼的运动较为稳定，可以保证患者的康复训练效果，同时也不会因过大的角加速度而造成患者的二次创伤。

3.3 样机实验验证

本文让使用者穿戴手部康复外骨骼后做5 min持续性屈伸运动，进行了样机实验验证。穿戴手部康复外骨骼后手指伸直状态和弯曲状态分别见图13、图14。

图13 穿戴手部康复外骨骼后手指伸直状态

图14 穿戴手部康复外骨骼后手指弯曲状态

4 结 语

本文提出了一种基于直线电机和连杆滑槽结构的手部康复外骨骼的机械设计和控制方案，设计了一种新型的机械结构，使手部康复外骨骼通过直线电机推杆的行程变化带动连杆滑槽结构，进行类似手指动作轨迹的运动，从而帮助患者进行康复训练。通过受力分析、运动学分析以及仿真验证，该手部康复外骨骼能够满足患者的手部运动需求，实现康复训练动作。样机验证说明，该手部康复外骨骼适用于高强度重复性的偏瘫康复训练。