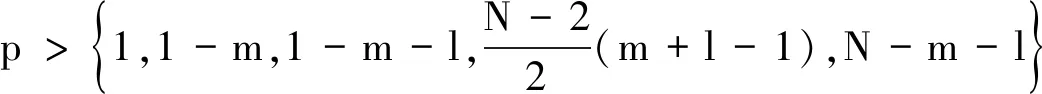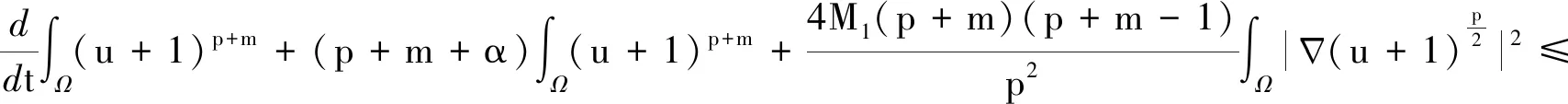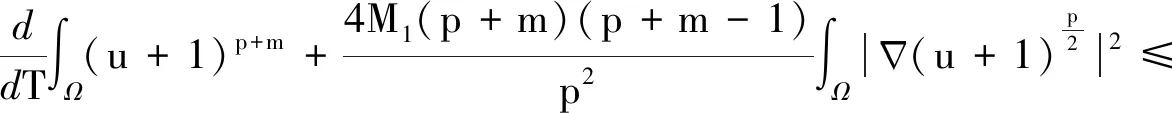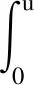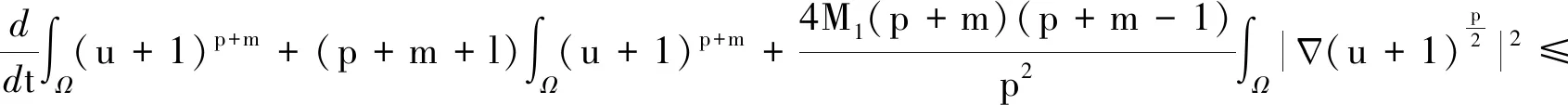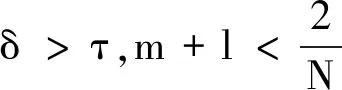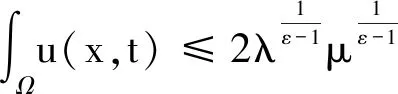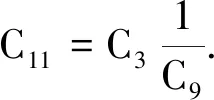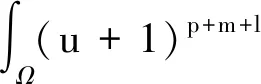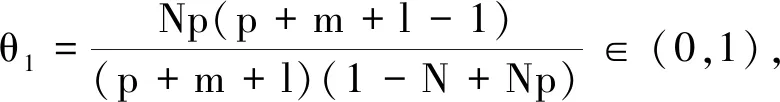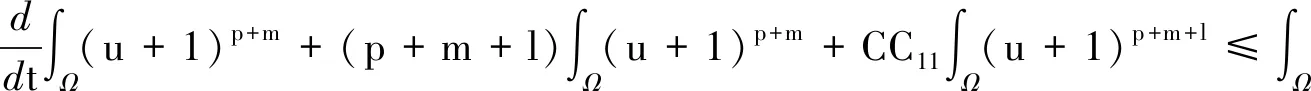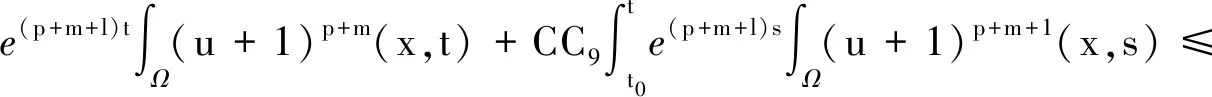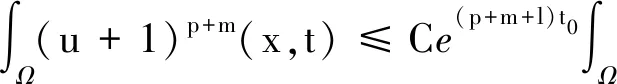具有间接信号生成和一般Logistic源的趋化模型解的整体有界性
吴顺军,许 璐
(伊犁师范大学数学与统计学院,新疆 伊犁 835000)
0 引言
本文讨论一类具有间接信号生成和一般Logistic源的拟线性趋化模型:
(1)
D(u),S(u)∈C2[0,∞),D(u)≥M1(u+1)-m,S(u)≥M2u(u+1)l-1,
(2)
其中,M1,M2>0且m,l∈R.初始值(u0,v0,w0)满足:
u0∈C0(Ω),v0∈w1,∞(Ω),w0∈C1(Ω)且u0,v0,w0≥0.
(3)
(4)
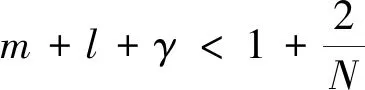
定理1 设Ω∈RN,N≥2,若α>1,μ>0, 并且初始值满足(3),则存在非负函数(u,v,w),
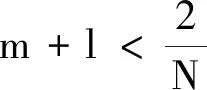

注释1 当τ=0,δ=1时,本文与文献[7]定理1的结论一致.
1 预备知识
首先给出解的局部存在性引理.由于解的局部存在性可由Amann’s定理得到,为了简便起见,省略证明过程.
引理1 令Ω⊂RN,N≥2是有光滑边界∂Ω的有界区域,D(u),S(u)满足(2).参数μ,τ,δ>0,初始值满足(3).那么存在Tmax∈[0,∞),使得模型(1)有唯一经典解(u,v,w).进一步,如果Tmax<∞,则当t→Tmax时,有

引理2 存在t0=t0(λ,μ,u0,Ω)>0,对任意的t∈(t0,Tmax),使模型(1)的经典解(u,v,w)满足:
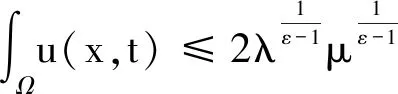
(5)
具体证明过程可参考文献[8]引理2.2的证明.
接下来介绍后续证明所用到的基本引理,具体证明过程可参考文献[9-11].
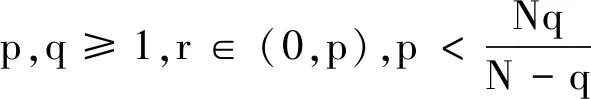

(6)

引理4 设0 (7) 定理2 设λ,μ>0,α>1且D(u),S(u)满足(2)式,当p>max{1-m,1}时,任意t∈(0,Tmax),存在C1=C1(p,m,l)>0,C2=C2(p,m,l,α,M1,M2,λ,μ,Ω)>0,使得 (8) 证明 将模型(1)的第一个方程乘以(u+1)p+m-1,并在Ω上积分,对任意t∈(0,Tmax),可得到 (9) (10) 整理公式(9)(10)可知,对任意t∈(0,Tmax),可得到 (11) 通过进一步计算,可以得到 (12) (13) 其中,C3=C3(p,m,l,α,λ,μ,Ω)>0 ,C3是常数.进一步整理(11)(12)(13),对任意t∈(0,Tmax),可得 (14) 其中,C4=C4(p,m,l,α,λ,μ,Ω)>0 .进一步,由Young不等式可得 (15) 其中,C5=(p,m,l,α)>0.整理式(14)(15)得到(8). 定理3 设δ,τ>0,对任意s∈(0,Tmax),ε∈(0,δ),存在C6=C6(p,m,l,δ,ε)>0,使得 (16) 证明 将模型(1)的第三个方程乘以wp+m+l并在Ω上积分,再通过Young不等式即可得到上式. (17) 证明 由引理1可知,当t>0时,模型(1)的经典解(u,v,w)有 (18) 由引理3可知,模型(1)的第二个方程对任意的t>t0,存在C,使得 (19) 接下来为了方便计算,令 (20) (21) 当C9<0时,进一步整理可得 (22) 再由Young不等式得到 (23) (24) 其中,C12=C12(p,m,l,λ,μ,Ω)>0,C13=C13(p,m,l,λ,μ,τ,δ,ε,Ω)>0. 整理公式(8)(23)(24)可得 (25) 其中,C14=C14(p,m,l,λ,μ,M1,M2,τ,δ,ε,Ω)>0. 对(25)运用常数变易法,并将(19)(22)代入可得 (26) 对任意t>t1>t0,有 (27) 再由标准的Alikakos-Moser迭代就完成了定理1的证明.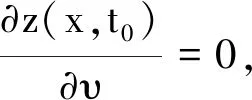
2 解的整体有界性