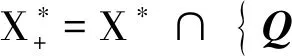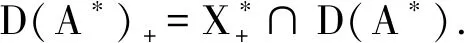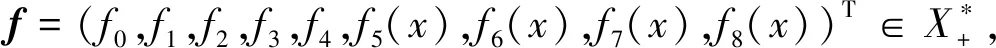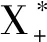多状态燃气电力可修系统主算子的性质

唐 慧，杨翔宇

(长春师范大学数学学院，吉林 长春 130032)

0 引言

多状态可靠性模型能够更真实、更精确地描述工程系统，多状态可靠性模型逐渐成为可靠性领域研究的热点问题.目前多状态可修系统分析方法有很多，如史跃东等[1]以模糊多状态船用汽轮发电系统为研究对象，利用模糊状态理论和发生函数算法建立了一种复杂装备系统的模糊多状态可靠性模型，给出了系统可用度的评估.史跃东等[2]针对时变需求约束下多状态装备系统，通过构建逻辑报酬矩阵体系给出了一种系统可靠性累计特征分析与评估的通用解算方法.张婷婷等[3]利用离散马尔可夫过程方法研究了一个具有M+1个状态的系统，并给出在状态i时的可靠度函数、平均寿命以及剩余寿命的解析表达式.王丽花[4]、EI-DAMCESE[5]、MANGEY[6]等根据系统实际假设和状态转移图，结合广义马尔可夫过程理论建立了一个系统状态微分方程组，并给出了稳态可用度及其数值算例.目前相关研究多注重于系统可靠性特征分析，而对于系统模型的分析较少.基于此，本文在文献[6]基础上对系统模型的主算子进行分析，并利用共尾理论和算子半群理论证明了系统主算子的谱上界与其生成半群的增长界相等.

1 系统模型

利用补充变量方法和马尔可夫过程理论，MANGEY[6]给出了由发电机、燃气轮机、压缩机、燃烧室、燃料和喷嘴等六个不同的部件组成的多状态燃气电力可修系统模型.该系统包含三种状态，即良好状态、退化状态和故障状态.系统只有一个修理设备，当系统发生故障时，可由修理设备对其进行修复，并且系统修复如新.在初始阶段，假设系统所有部件都处于良好状态，系统状态转移过程如图1所示.

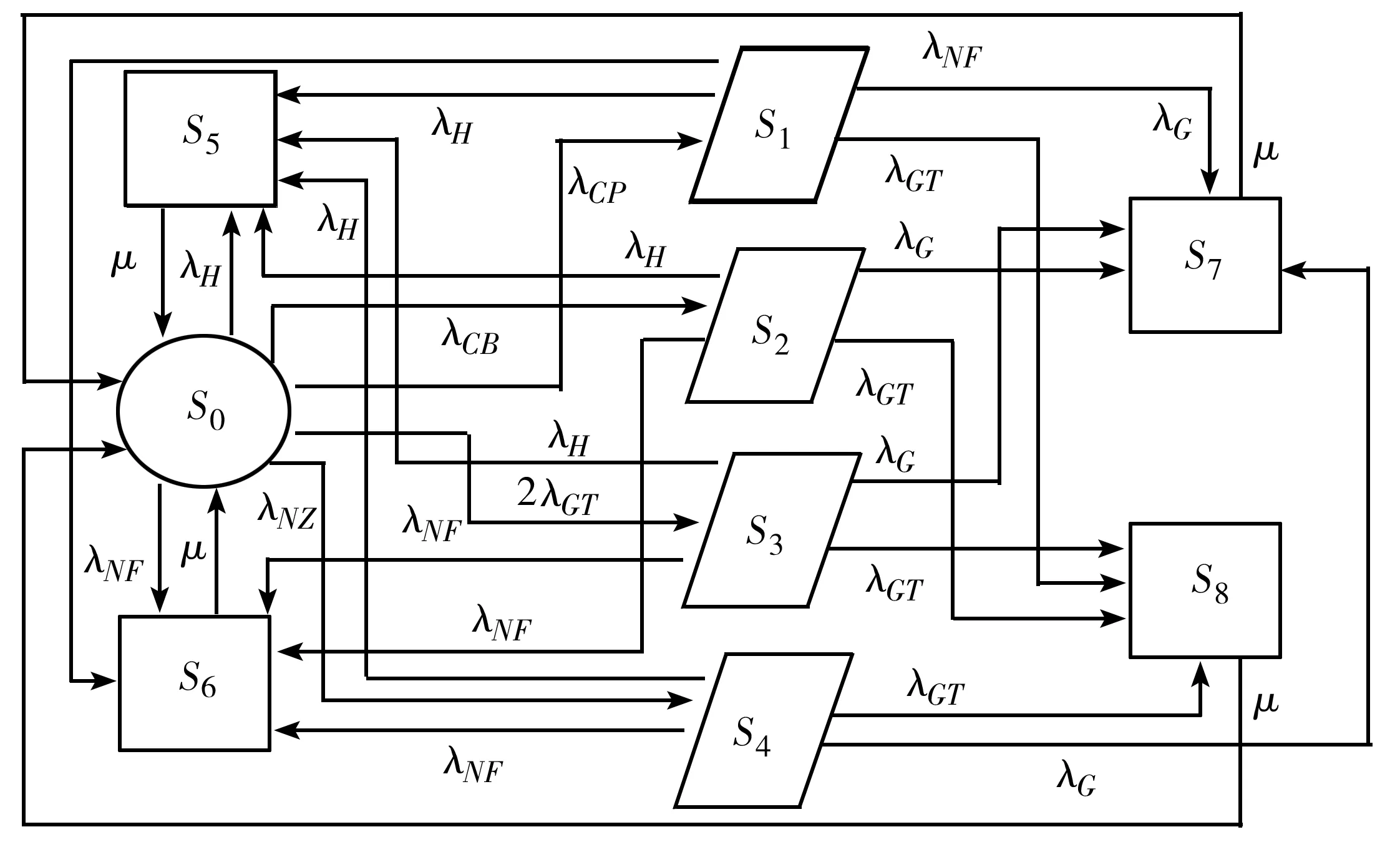
图1 状态转移图

系统状态说明：状态0表示所有组件良好且均正常工作，即状态为良好状态；状态1表示压缩机故障，故障率为λCP，其他部件正常工作，即系统处于退化状态；状态2表示燃烧室故障，故障率为λCB，其他部件正常工作，即系统处于退化状态；状态3表示辅助燃气轮机故障，故障率为2λGT，其他部件正常工作，即系统处于退化状态；状态4表示喷嘴故障，故障率为λNZ，其他部件正常工作，即系统处于退化状态；状态5表示由于人为故障而导致的故障状态，人为故障率为λH；状态6表示由于缺失燃料而导致的故障状态，燃料的可用性故障率为λNF；状态7表示由于发电机故障而导致的故障状态，发电机故障率为λG；状态8表示由于主燃气轮机故障而导致的故障状态，主燃气轮机故障率为λGT.

此系统模型可以由下面的微积分方程组描述：

边值条件：

P5(0,t)=λH[P0(t)+P1(t)+P2(t)+P3(t)+P4(t)],
P6(0,t)=λNF[P0(t)+P1(t)+P2(t)+P3(t)+P4(t)],
P7(0,t)=λG[P1(t)+P2(t)+P3(t)+P4(t)],
P8(0,t)=λGT[P1(t)+P2(t)+P3(t)+P4(t)].

初值条件：

P0(0)=1，其余为0.

其中，Pi(t)表示时刻t系统处于状态i的概率，i=0,1,2,3,4；Pj(x,t)表示时刻t系统处于状态j且修复时间为x的概率，j=5,6,7,8；λG表示部件发电机的故障率；λGT表示部件燃气轮机故障率；λCP表示部件压缩机故障率；λCB表示部件燃烧室故障率；λNF表示燃料的可用性故障率；λNZ表示部件喷嘴故障率；λH表示人为故障率；μ表示状态j到良好状态的修复率.

其中,a0=λH+λCP+λCB+2λGT+λNZ+λNF，a1=a2=a3=a4=λG+λH+λGT+λNF，Pj(x)绝对连续,j=5,6,7,8，D(B)=X.因此系统可以转化为Banach空间X中的抽象Cauchy问题：

2 系统主算子性质

定义1 设集合C为集合E的子集，若对任意的f∈E，存在g∈C，使得f≤g，则称C在E中共尾.

定义3 设B是一个正的C0半群(T(t))t≥0的生成元，则称

为算子B的增长界.

定理1D(A)在X中稠.

定理2 主算子A是预解正算子.

证明 对于任意的Y∈X，考虑算子方程(γI-A)P=Y，即

(γ+ai)Pi=yi,

解上述方程可得

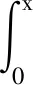
其中，i=0,1,2,3,4,j=5,6,7,8.

结合边界条件，可得

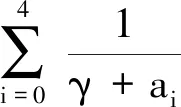
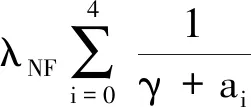
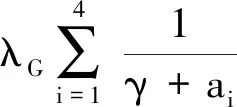
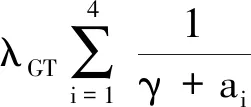
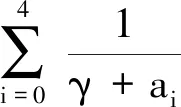
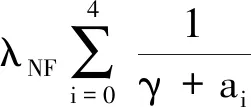
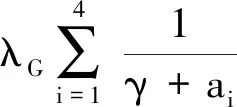
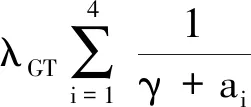
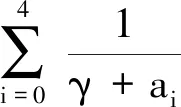
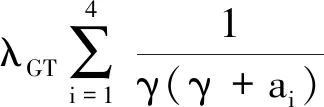
定理3 当γ≥-μ时，γ∈ρ(A).

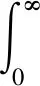
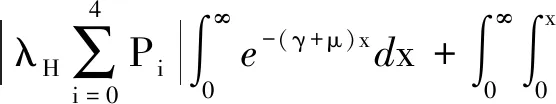
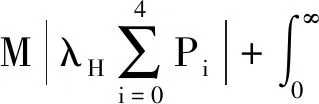
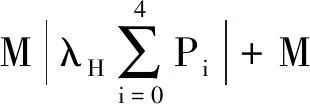
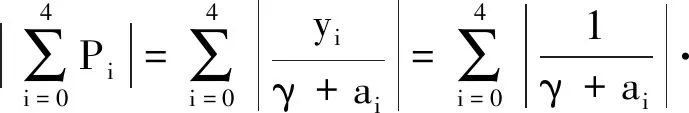
同理，

综上可知，

定理4 当γ<-μ时，γ∈σ(A)，并且s(A)=-μ.

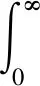
由文献[9]易知，X的对偶空间X*如下：

定理5 主算子A的对偶算子A*为

其中，Qj(x)∈L∞(R+)绝对连续.

证明 对∀P∈D(A)，∀Q∈X*，有

[-(λH+λCP+λCB+2λGT+λNZ+λNF)Q0+λHQ5(0)+λNFQ6(0)]P0+

[-(λG+λH+λGT+λNF)Q1+λHQ5(0)+λNFQ6(0)+λGQ7(0)+λGTQ8(0)]P1+

[-(λG+λH+λGT+λNF)Q2+λHQ5(0)+λNFQ6(0)+λGQ7(0)+λGTQ8(0)]P2+

[-(λG+λH+λGT+λNF)Q3+λHQ5(0)+λNFQ6(0)+λGQ7(0)+λGTQ8(0)]P3+

[-(λG+λH+λGT+λNF)Q4+λHQ5(0)+λNFQ6(0)+λGQ7(0)+λGTQ8(0)]P4+

定理6 系统的主算子A生成一个正的C0半群，并且s(A)=ω(A)=-μ.