基于拉压杆理论的桥墩结构受力分析
贺 科 杜 磊 谭巨良 曹 清
(广东省交通规划设计研究院集团股份有限公司 广州 510507)
随着高速公路建设中对景观方面的要求越来越高[1],为满足桥梁的景观要求,以Y形墩、花瓶墩为代表的一系列异形墩的应用越来越广泛。但由于异形墩的墩形特殊,其受力相对复杂,采用常规的拉压杆模型对其进行分析计算会产生较大的误差。因此,本文将基于拉压杆模型计算理论,结合实体有限元方法,对花瓶墩和Y形墩进行受力分析,并提出合理的设计建议。
1 拉压杆模型基本理论
拉压杆模型是根据桁架模型,经过多年的理论发展得出的一种理论计算方法,主要适用于混凝土结构中力流扰动较大的区域[2]。例如,深梁体系、端部锚固区、桥墩结构、梁端位置等等。这种方法的优势在于可以模拟混凝土内部结构的实际传力情况,使得内外部荷载达到平衡状态,同时还可以满足混凝土的塑性变形限制的要求[3]。
1.1 基本理论
拉压杆模型是针对结构D区(应力扰动区:结构不满足平截面假定的区域)的一种简化模型。结构D区主要存在于集中力、截面形式突变处[4]。桥梁结构中,支座、锚点位置均为集中力作用,横梁、横隔板等位置存在截面突变,因此,以上局部区域的受力较为复杂,不再满足平截面假定,对此类区域进行分析时,可采用拉压杆模型进行简化分析。
1.2 构形方法
目前常用的拉压杆模型的构形方法有:荷载路径法、应力迹线法、力流线法、最小应变能准则、最大强度准则等[5]。
由于桥墩构造及自身的传力路径,形成了在桥墩顶两支座之间拉应力集中现象[6-7]。因此可以通过有限元软件ABQUS求得结构的主应力迹线从而简化得到结构的拉压杆模型。
1.3 模型验证
为验证应力迹线法的准确性,以JTG 3362-2018 《公路钢筋混凝土及预应力混凝土桥涵设计规范》(以下简称《规范》)中附录B.1.2的深梁体系及端部锚固区的拉压杆简化模型为例进行分析。
1.3.1深梁
《规范》中深梁简化的拉压杆模型见图1,实体有限元分析得到的深梁体系的主应力方向见图2及图3。对比图1~图3可见,《规范》中简化的拉压杆方向与结构主应力方向基本一致。

图1 深梁体系拉压杆简化模型(《规范》B.1.2-a)
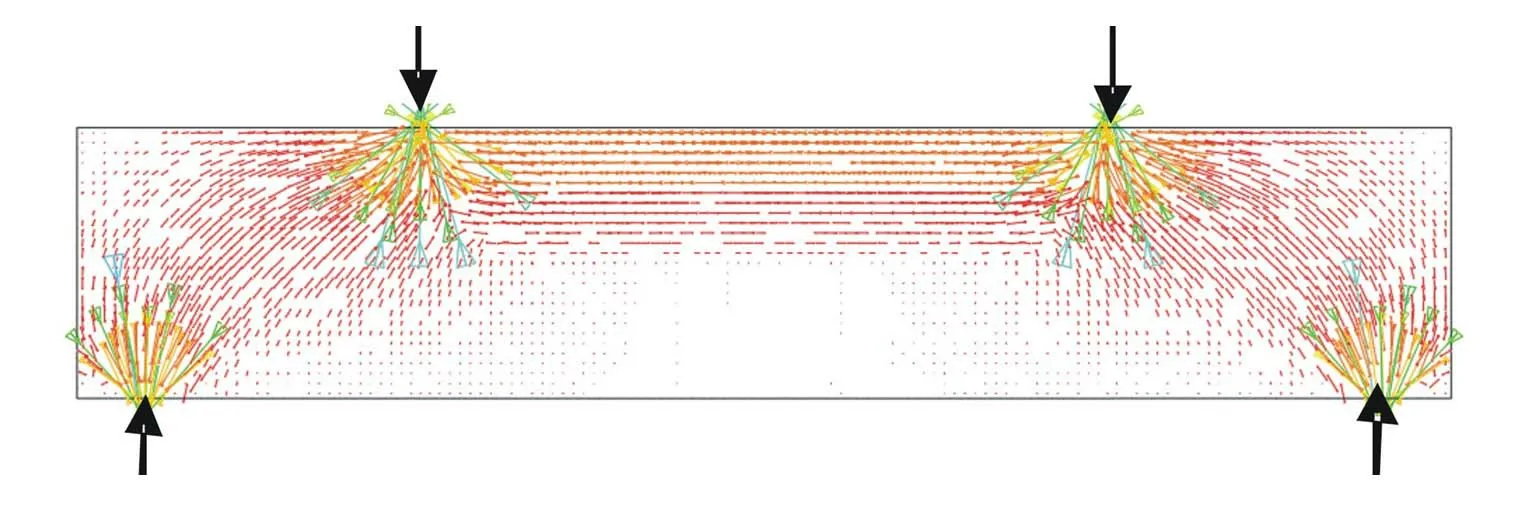
图2 深梁体系主压应力方向图

图3 深梁体系主拉应力方向图
1.3.2端部锚固区
《规范》中端部锚固区简化的拉压杆模型见图4,实体有限元分析得到的端部锚固区的主应力方向见图5及图6。对比图4~图6可见,《规范》中简化的拉压杆方向与结构主应力方向基本一致。

图4 端部锚固区拉压杆简化模型(《规范》B.1.2-b)

图5 端部锚固区主压应力方向图
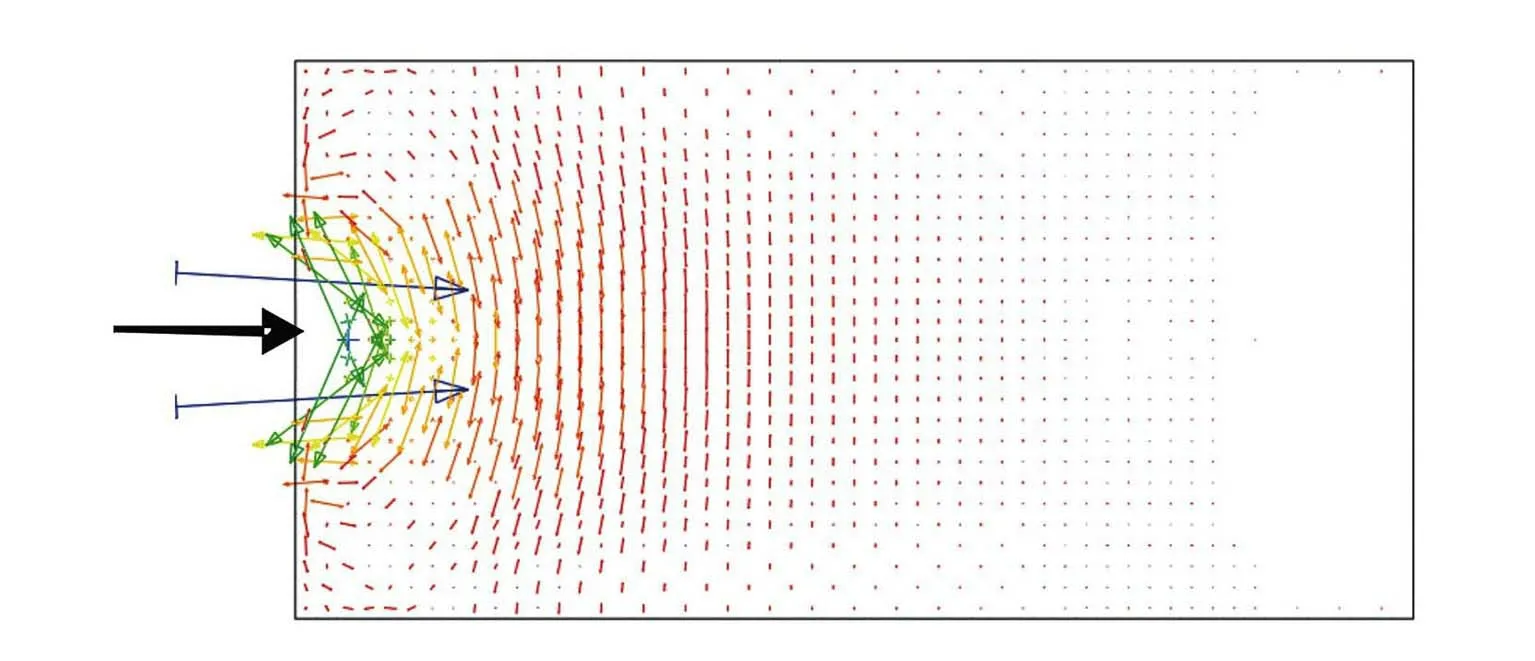
图6 端部锚固区主拉应力方向图
2 拉压杆模型在桥墩结构中的应用
2.1 规范公式
《规范》8.4.7中对于布置双支座的独柱墩(矩形、倒梯形、花瓶形)的墩帽可采用的拉压杆模型,见图7。

图7 3种独柱墩帽的拉压杆模型(《规范》8.4.7)
由图7可见,《规范》假设拉杆距墩顶距离为h/9,距离下缘水平压杆5h/9,根据节点力平衡可得
式中:Fd为墩顶竖向力设计值,kN;Tt,d为墩顶横向拉杆内力设计值,kN;s为双支座中心距,m;h为墩顶横向变宽度区的高度,m;b′为距离墩顶高度为h位置处,墩帽或墩身的横向宽度,m。
化简可得《规范》中顶部横向受拉部位即拉压杆模型中拉杆的拉力计算式见式(1)。
(1)
2.2 花瓶墩的受力分析
2.2.1理论计算
图8为某一实际项目中的花瓶墩示意图,其中墩顶竖向力设计值Fd为3 000 kN,支座中心距s为2.8 m,距离墩顶高度为h位置处,墩帽或墩身的横向宽度b′为2.6 m,墩顶变宽度区高度h为2.6 m。由此,根据式(1)计算得到墩顶横向拉杆的拉力为1 558 kN。

图8 独柱墩帽的拉压杆模型(《规范》8.4.7)(单位:cm)
2.2.2模型分析
建立花瓶墩的实体有限元模型见图9,其中花瓶墩墩身采用三维实体单元模拟,共54 648个单元,墩底固结,墩顶支座位置施加竖向集中力。该墩的主应力方向图见图10,对比花瓶墩的主应力方向及《规范》提供的花瓶墩的拉压杆模型(见图7c)),可以看出,花瓶墩的主应力方向与《规范》的拉压杆方向基本一致。

图9 花瓶墩有限元模型图 图10 花瓶墩主应力方向
对墩顶受拉区域截面进行积分,得到拉杆拉力见图11,拉杆拉力为1 373 kN,与《规范》公式计算得到的1 558 kN误差为13%。

图11 花瓶墩拉杆拉力云图(单位:N)
2.2.3参数分析
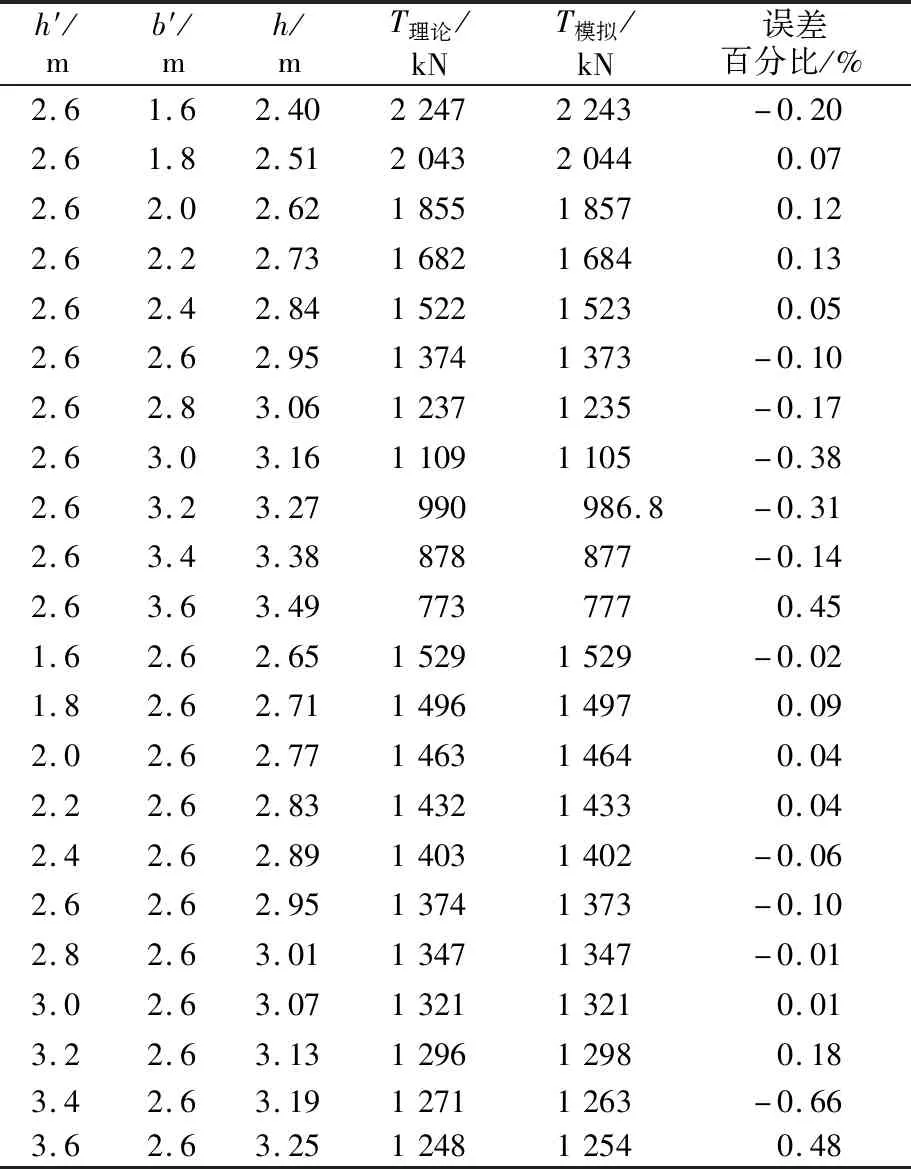
《规范》公式中Fd、s、b′在结构确定时均为定值,因此,当墩顶横向变宽度区的高度h为确定时,拉杆拉力也为定值。而《规范》中关于花瓶墩h的取值当h>b时取h=b,当h h=f(h′,b′) 式中:h为墩顶横向变宽度区的高度,m;h′为花瓶墩圆弧与直线的交点至墩顶的距离,m;b′为距离墩顶高度为h位置处,墩帽或墩身的横向宽度,m。 为对比分析花瓶墩墩顶拉杆拉力的影响因素,在控制支座位置及荷载的情况下,分别调整墩h′及b′并建模计算墩顶拉杆拉力。花瓶墩尺寸示意见图12。 图12 花瓶墩尺寸示意图(单位:cm) 表1为h′固定、调整b′时的拉杆拉力结果统计表,图13为根据表1绘制得到的h-b′曲线图。 表1 花瓶墩拉杆拉力计算结果统计表 图13 花瓶墩拉杆拉力b′-h曲线图 由图13可见,h与b′为线性关系。同理,b′固定,调整h′的拉杆拉力结果统计见表2,图14为根据表2绘制得到的h′-h曲线图。 表2 花瓶墩拉杆拉力计算结果统计表 图14 花瓶墩拉杆拉力h′-h曲线图 根据表2和图14可以看出h与h′为线性关系。因此,可假设h的计算式见式(2)。 h=a1b′h′+a2b′+a3h′+a4 (2) 拟合图13和图14中的曲线可得 h=0.544b′+1.533 6 h=0.298 5h′+2.170 6 (3) 对于矩形墩,即当b′=b时,h=b,即 h=a2b=b (4) 根据式(2)~(4)可联立求解,得到墩顶横向变宽度区的高度h的计算公式如下。 h=-0.175 4b′h′+b′+0.754 5h′-0.429 4 (5) 表3为图12尺寸花瓶墩的拉杆拉力对比表。由表3可见,当采用式(5)计算墩顶横向变宽度区的高度h从而计算墩顶拉杆横向拉力时,与有限元模拟结果吻合良好。 表3 花瓶墩拉杆拉力对比表 2.2.4非对称荷载分析 对于曲率大的斜弯桥,桥墩荷载不一定对称,即桥墩处左、右支座的支座反力不一定相同。为分析非对称荷载作用下墩顶拉杆横向拉力情况,采用2.2.2中花瓶墩模型,调整桥墩右侧支座反力,对比有限元分析结果及理论计算结果。左侧支座反力为3 000 kN,右侧支座反力为1 000 kN时对墩顶受拉区域截面进行积分,得到拉杆拉力见图15,由图15可见,支座中心处截面拉杆拉力为915.4 kN。 图15 花瓶墩拉杆拉力云图(单位:N) 将右侧支座反力分别调整为1 000~5 000 kN,墩顶拉杆拉力的理论计算结果及有限元计算结果见表4。由表4可见,采用式(5)进行理论计算结果与有限元模拟结果吻合良好。 表4 非对称荷载下花瓶墩拉杆拉力对比表 图16为某项目TY墩的立面图。 图16 TY墩立面图 其中墩厚4 m,墩顶盖梁横桥向长37.4 m,盖梁顶向下11.5 m为Y形分支墩,截面高度从3.5~4.35 m,再向下墩身从8 m开始,以1∶25的斜率渐宽。墩身为薄壁空心墩,纵桥向壁厚80 cm,横桥向壁厚最大处为120 cm。墩顶共4个支座,单个支座竖向力设计值为15 000 kN。 TY墩的实体有限元分析模型见图17,其中TY墩墩身采用三维实体单元模拟,共143 404个单元,墩底固结,墩顶支座位置施加竖向集中力。提取Y肢处的主应力图见图18,图中红色区域为主拉应力,蓝色区域为主压应力。由图18可见,结构盖梁主要承受拉应力,Y肢主要承受压应力,Y肢悬臂处受力较为复杂。对墩顶受拉区域截面进行积分,得到拉杆拉力图见图19,拉杆拉力为37 110 kN。 图17 TY墩计算模型图 图18 TY墩Y肢处主应力图 图19 TY墩拉杆拉力图(单位:N) 若采用规范公式计算TY墩墩顶拉杆拉力,由于TY墩主应力方向与规范等效的拉压杆模型方向不一致,因此计算结果与实体有限元模型分析结果误差较大,此处不列出具体的计算过程及结果。 为计算TY墩墩顶拉杆拉力,根据TY墩主应力方向得到结构等效拉压杆模型后,基于拉压杆模型理论对拉杆拉力进行求解,TY墩墩顶支座布置图见图20。 图20 TY墩墩顶支座布置图(单位:mm) 为简化分析,对内外侧支座处荷载效应单独分析。图21为内侧支座(支座2、支座3)处竖向荷载作用下结构Y肢处的主应力图,由此可等效出结构拉压杆模型见图22。因此在支座竖向力荷载为15 000 kN时,根据节点力平衡可得到墩顶拉杆拉力也为15 000 kN。 图21 TY墩主应力图 图22 TY墩等效拉压杆 模型(单位:mm) 由于支座1位于结构悬臂位置,因此将作用于支座1处的竖向荷载等效为支座2处的竖向荷载及弯矩。支座1处竖向荷载为15 000 kN,等效为支座2处的竖向荷载为15 000 kN,弯矩为15 000×5.5=82 500 kN·m。支座4处竖向荷载同理可等效为支座3处荷载。 根据图22的等效拉压杆模型,当支座2、3作用15 000 kN的竖向力时,拉杆拉力为15 000 kN;当支座2、3处作用82 500 kN·m的弯矩时,拉杆拉力为82 500/9.5=8 684 kN。 综合以上分析,可以得出TY墩在竖向力荷载作用下,墩顶拉杆拉力大小为38 684 kN。对比有限元计算得到的拉杆拉力为37 110 kN,误差为4.2%。 本文结合《规范》中双支座独柱墩墩帽拉杆拉力的计算公式,以实际工程项目为例,对比分析花瓶墩及TY墩中拉杆拉力大小的理论值及有限元模拟值,得到以下结论。 1) 花瓶墩墩顶横向变宽度区的高度h与距离墩顶高度为h位置处桥墩宽度b′为线性关系。 2) 花瓶墩墩顶横向变宽度区的高度h与花瓶墩圆弧与直线交点至墩顶高度h′为线性关系。 3) 提供了一种关于花瓶墩墩顶横向变宽度区高度h计算公式的拟合方法,为相关工程提供参考。 4) 对于结构受力形式较为复杂的异形墩如TY墩等,采用《规范》公式对墩顶拉力进行计算时误差较大,需采用有限元方法对其进行单独的受力分析求解。采用实体有限元分析是比较精确的方法,若采用规范拉压杆计算,压杆角度可以采用Y肢倾斜角,或根据实际结构进行分析。






3 TY复合墩的受力分析
3.1 工程概况

3.2 模型分析



3.3 TY墩墩顶拉杆拉力计算


4 结语

