管道悬索桥静气动性能研究*

周傲秋 宋洪芳 孙传智

(1.宿迁学院建筑工程学院 宿迁 223800； 2.营口市海洋预警监测中心 营口 115007)

管道桥用于运输天然气，石油或水，途中常需跨越江河、峡谷深沟等阻碍。管道悬索桥体系受力合理、跨越能力强，且施工方便，因此被广泛运用于油气输运工程中[1]。与公路悬索桥相比，管道悬索桥主梁宽跨比小、刚度低，因此对风荷载较为敏感。若管道遭强风损坏，引起石油或天然气发生泄漏，可能导致火灾或爆炸，造成人员伤亡和环境污染。因此保证管道跨越工程的安全运营具有重大意义。

在未来20年内，我国将持续推进中国西南地区油气管网建设[2]。管道悬索桥构造复杂，包括加劲梁、管道、篦子板和栏杆等，国内外学者对其气动特性进行了广泛的研究。段银龙等[3]利用风洞试验得到怒江管道桥的静三分力系数，通过ANSYS研究风缆倾角、风缆索力、管道位置、输送介质质量对结构静动力特性的影响，并给出了主索、桥塔和管道安装的设计优化方法；方国辉[4]以澜沧江管道悬索桥为工程背景，对其颤振临界风速、静风稳定性，以及颤振临界风速影响因素等方面进行分析，结果表明，结构布置形式、主梁截面形状、风缆夹角α、主缆风力，以及风攻角均是影响静风稳定性的重要因素；王凯等[5]通过风洞试验研究了中缅油气管道悬索桥风致振动响应，结果表明，跨度300 m以下的桁架管道桥具有很好的抗风稳定性。

以往研究一般针对某座悬索管道桥的振动进行分析,而未进行该类桥梁的分类研究。管道作为管道悬索桥的核心构件之一，需满足工程所需的不同设计要求，如管道直径、管道数量、管道横向间距等，上述因素均可能影响管道悬索桥的抗风性能。因此，有必要研究管道布置形式对管道悬索桥气动特性的影响，为有效完善管道悬索桥的抗风设计规范提供可靠的参考依据。

1 静风荷载

平均风流经结构断面时，会在结构上施加静力风荷载。静力风荷载包含阻力、升力和扭矩3个分量。阻力由断面迎风面与背风面的压力差形成，升力由断面上、下表面的压力差形成，扭矩由两者合力偏心作用在断面形成。静三分力坐标系表示方法分为体轴坐标系——沿截面形心主轴建立和风轴坐标系——坐标系沿风向建立[6]，静三分力坐标系见图1。

图1 静三分力坐标系

体轴三分力[7]计算方法见式(1)～(3)。

(1)

(2)

(3)

式中：U为试验风速；ρ为空气密度；L为节段模型长度；B为模型宽度；H为模型高度；FH(α)、FV(α)和MZ(α)分别为攻角α下的阻力、升力和扭矩，α为风攻角。

风轴与体轴的三分力换算关系见式(4)～(5)。

FD(α)=FH(α)cosα+FV(α) sinα

(4)

FL(α)=FV(α)cosα-FH(α) sinα

(5)

则风轴三分力系数见式(6)～(8)。

(6)

(7)

(8)

2 风洞试验

2.1 试验设备

该风洞为全钢结构单回流闭口式边界层风洞，风洞试验段尺寸长18 m、宽3 m、高2.5 m，阻塞率小于5%，可进行小尺寸模型的风洞模拟试验，模拟精度良好，设计最大风速50 m/s，配备可以旋转0°～360°的β机构转盘，其旋转最小间隔0.1°。测力天平系统采用日本NITTA公司六分量高频测力天平，量程FX=FY=315 N，FZ=630 N，MX=MY=MZ=63 N·m，精度0.06%，天平采样时间为30 s，数据采样频率为200 Hz。

2.2 试验工况

在管道悬索桥设计时，需考虑油气需求量、能源需求种类与检修通道的位置及尺寸等因素，其分别影响着管道直径、管道数量与管道间距等参数，上述参数的改变可能会对悬索桥静气动性能产生不利影响，故有必要研究其对断面静三分力系数的影响。

风洞测力试验以某管道悬索桥为研究对象，实桥断面宽B=2 680 mm，高T=1 680 mm，受风洞尺寸限制，试验制作缩尺比为1∶5的节段模型，缩尺后的桥梁断面宽B=536 mm，高T=336 mm，模型节段长取1 000 mm。管道、篦子板及栏杆均采用PVC材料加工。模型的桁架采用铝材制作，模型底部与测力天平通过多个螺栓连接，避免模型与天平产生相对滑动而产生附加惯性力。模型顶部悬挂一块1.2 m×1.2 m的端板用于满足结构周围的二元流动假设。断面示意图见图2。

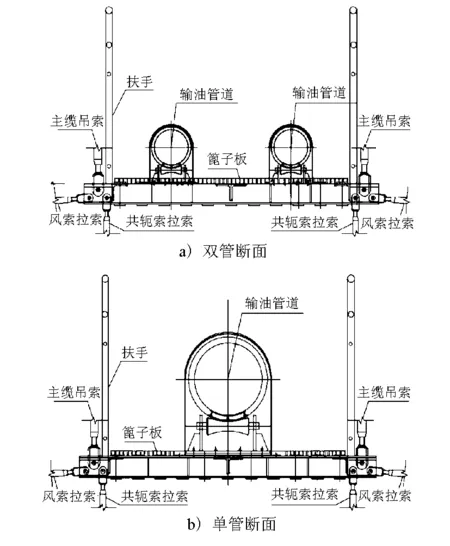
图2 模型断面示意图

试验共分3种类型。选取D=70、160、250 mm的管道，分析管道直径对桥梁断面静三分力系数的影响；选取D=70 mm和D=160 mm的管道，分析管道数量对桥梁断面静三分力系数的影响；选取D=70 mm的管道，改变管道横向间距L=120，170，220，245，270 mm，分析管道横向间距对桥梁断面静三分力系数的影响。

以上试验工况均在均匀流场中进行，攻角α在-12°～12°范围内变化，增量为1°。需要注意的是，缩尺后的桥梁断面可能存在雷诺数效应，故试验选取10级风速，通过风速变化，研究雷诺数对断面静三分力系数的影响。雷诺数试验在均匀流场中进行，试验攻角α=0°。

试验工况表见表1，模型风洞试验图略。

表1 试验工况

2.3 试验结果与分析

2.3.1管道直径的影响

试验结果见图3。

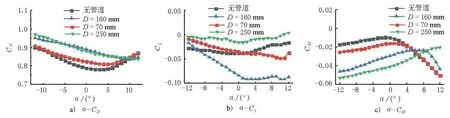
图3 考虑管道直径的静三分力系数(15.51 m/s)

由图3可知：

1) 在试验攻角范围内，随着攻角增大，断面阻力系数CD均先减小后增大，且极小值对应的攻角α随直径增大而增大，分别为3°，4°，9°，11°；当断面无管道和D=250 mm时，断面升力系数CL基本不变，D=70 mm和160 mm时的断面升力系数CL随α的增加而增大；随着攻角增大，断面扭矩系数CM均先增大后减小，且极大值对应攻角随直径增大而增大，分别为-1°、1°、7°、12°。

2) 管道的设置显著增大了断面的阻力系数和升力系数，且阻力系数值CD和升力系数值CL均随着D的增大而增大；在α=-12°～7°范围内，断面扭矩系数CM随着D的增大而增大，在α=7°～12°范围内则相反。

总的来说，管道直径D的增大，大幅增大了断面的静三分力系数，原因是由于试验攻角α改变后，气流在主梁下风侧产生更大的漩涡，而上风侧气流变化不大，从而产生较大幅度的压力差变化。故在设计阶段应充分考虑管道直径D对断面静三分力系数的影响。

2.3.2管道数量的影响

试验结果见图4。

图4 考虑管道数量的静三分力系数(15.51 m/s)

由图4可知：

1) 当D=70 mm时，随着攻角α增大，断面阻力系数CD均先减小后增大，且极小值对应的攻角α随管道数量的增加而增大，分别为3°、4°、5°，断面升力系数CL均先增大后减小，极大值对应的攻角α分别为-1°、10°、4°，断面扭矩系数CM均先减小后增大，且极小值对应的攻角α随管道数量的增大而增大，分别为-1°、1°、3°；当D=160 mm时，随着攻角α增大，断面阻力系数CD均先减小后增大，且极小值对应的攻角α随管道数量的增加大而增大，分别为3°、7°、10°，断面升力系数CL均先增大后减小，极大值对应的攻角α分别为-1°、5°、2°，断面扭矩系数CM均先减小后增大，且极小值对应的攻角α随管道数量的增大而增大，分别为-1°、8°、11°。

2) 管道的设置显著增大了断面的静三分力系数，该结论再次得到验证；且随着管道数量的增加，2种直径管道的断面静三分力系数均随之增大。

总的来说，管道数量的增加引起了断面静三分力系数显著增大，这是因为管道数量越多，气流透过桁架越困难，导致迎风面积的增大，从而引起静三分力系数的增大。故在管道直径的设计中应充分考虑管道数量对断面静三分力系数的影响。

2.3.3管道横向间距影响

试验结果见图5。

图5 考虑管道横向间距的静三分力系数(15.51 m/s)

由图5可知：

1) 随着攻角α的增加，阻力系数CD值均先减小后增大，在α=6°时均达到极小值；升力系数CL均先增大后减小，均在α=5°左右达到极大值；扭矩系数CM均先减小后增大，均在α=3°左右达到极小值。

2) 通过几种工况的对比，再次得出结论：管道的设置会引起断面静三分力系数的显著增大；且断面静三分力系数受管道横向间距的影响均很小。

总的来说，管道横向间距L对断面静三分力系数的影响几乎可以忽略不计，这是因为管道数量相同的情况下，调整管道横向间距不会改变迎风面积，气流透过桁架的能力不发生改变，因此管道横向间距对静三分力系数影响很小。故在管道桥的设计阶段，可根据实际情况灵活调整管道横向间距。

2.3.4雷诺数效应

3种直径管道断面对应的雷诺数Re范围分别为0.37×105～1.42×105、0.89×105～3.4×105、1.39×105～5.3×105，测力试验结果见图6。

图6 考虑雷诺数效应的静三分力系数曲线

由图6可知，当配置D=160、250 mm单管道时，桥梁断面静三分力系数变化幅度不大；当配置D=70 mm单管道时，桥梁断面阻力系数CD随雷诺数Re增大而减小；升力系数CL在U<18.5 m/s时基本不变，在U>18.5 m/s时随Re的增大而减小；扭矩系数CM在U<18.5 m/s时基本不变，在U>18.5 m/s时随Re的增大而增大。当配置D=70、160 mm双管道时，桥梁断面阻力系数CD与升力系数CL均在U<10.4 m/s时随Re的增大而减小，当U>10.4 m/s后基本不变；2种桥梁断面的扭矩系数CM均基本不变。总的来说，D越小，雷诺数效应越明显。

3 结语

本文以某管道悬索桥为研究背景，制作缩尺节段模型进行风洞测力试验，研究风攻角、管道直径、管道数量、管道横向间距对静三分力系数的影响，并评估静三分力系数雷诺数效应，得到结论如下。

1) 管道直径的增大导致断面的阻力系数和扭矩系数值随之增大，同时引起升力系数值的大幅改变，在设计阶段应选择合适的管道尺寸。

2) 管道数量的增加导致断面的静三分力系数值随之增大，在设计阶段应选择合适的管道数量。

3) 管道横向间距对静三分力系数的影响几乎可以忽略不计，在设计阶段可灵活布置管道横向间距。

4) 相比大直径管道，无论桥梁设置单管或双管，小直径管道的桥梁断面雷诺数效应均更明显。

5) 需要注意的是，本文选择跨度较大的管道直径与间距的目的在于能全面模拟实际工程中不同管道直径、管道间距对断面静气动性能的影响，但本文仅初步分析了管道直径和间距的影响大小，截面优化及精度还有待进一步研究。