双正弦波纹柔性铰链的设计与分析

伍建军，王振飞

（江西理工大学 机电学院，赣州 341000）

0 引言

柔顺铰链相对于传统依靠固定铰链的多杆传动机构，结构更加简化，其通过构件的变形而产生力和位移[1]。目前精密定位技术广泛应用于微型机器人、生物科学研究以及工业生产等领域[2]。使用柔顺机构精密定位具有免装配、无摩擦等优点，避免了由于铰链间隙造成的误差[2]。基于柔顺机构的定位平台的工作空间受限于铰链的弹性形变范围，而传统矩形截面铰链和圆形截面铰链主要受剪切力形变，在遇到压拉力形变时，行程十分有限。田延岭等[3]设计出一种由弹性铰链作为其导向机构的串联微定位平台；崔玉国等[4]基于Stewart并联机构，研制出具有对称双圆弧薄板式弹性单元体的微动平台新构型；王念峰等人[5]设计了一种以半圆形波纹簧片的两自由度精密定位平台，着重进行了铰链的分析与有限元的对比，具有良好的解耦性。

综上所示，本文以实现输出位移大、结构紧凑的目标，提出了一种双正弦波纹的柔性铰链，在平面位移的两自由度上都具有良好的传导性，以此来替代传统刚性运动副进行力和位移的传导。分析传统铰链相比于波形铰链的不足之处，使用ANSYS将之进行单段和多段的对比分析验证双正弦波纹铰链的优势。

1 正弦波纹铰链设计

根据伯努利梁理论，对于一般悬臂梁的最大挠度可以用式(1)表示：

式中，δ为悬臂梁末端的挠度；F为施加在悬臂梁末端上的力；L为悬臂梁的长度；E为悬臂梁的弹性模量；I为转动惯量。其中，转动惯量I与悬臂梁的宽度b和厚度h有关，如式(2)所示：

因此，在材料和载荷不变的情况下，改变悬臂梁的长度以及宽和厚度便可以改变悬臂梁的最大挠度。假设悬臂梁的宽度与厚度不变，只改变其长度，可以将一般的悬臂梁设计为如图1所示的三角形和矩形周期性悬臂梁的形式[6，7]。然而，虽然增加了梁的长度，但由于在拐角处出现的尖锐角，极易产生应力集中的问题。

图1 三角形和矩形周期性悬臂梁

综上所述，又根据王念峰等人提出的半圆形波纹柔性铰链，如图2所示。考虑到其结构紧凑在y轴方向上的行程有所不足，若适当增加每半个波纹之间的距离，便可以有效改善这一现象。基于此设想一，本文提出了一种基于正弦的曲线波纹铰链，其公式如式(3)所示。

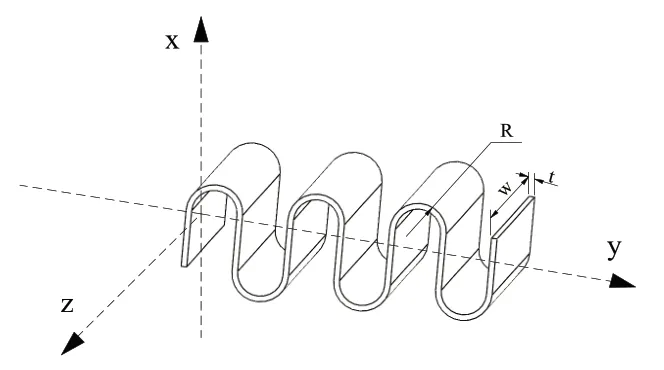
图2 半圆形波纹柔性铰链

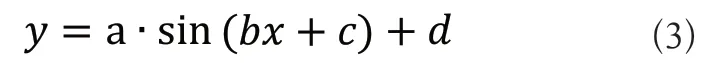
为对比两者的行程，将在下一节中采用有限元仿真对其进行静力分析，通过对比其x轴与y轴方向的最大位移来验证其性能。

2 有限元对比分析

为了便于传统矩形截面铰链和圆形截面铰链、半圆形波纹铰链以及正弦波纹铰链的对比，使其柔性部分总长、最薄弱处厚度、材料以及外力都统一。各铰链的柔性部分使用铝合金材料Al7075-T651。其中，半圆形波纹铰链的厚度t=0.1mm，w=10mm，R=1mm，正弦波纹则采用等距0.1mm来绘制，各参数取值分别为a=2，b=1，c=0，d=0，在ANSYS中将其进行静力学分析，如图3所示。

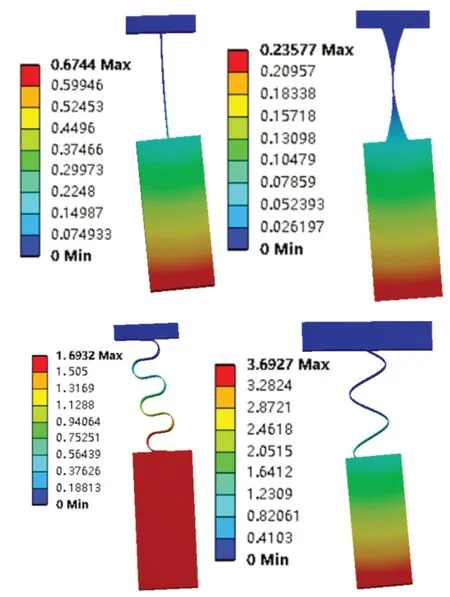
图3 各铰链x轴向位移云图

经有限元分析验证，在各外部条件都一致时，半圆形波纹柔性铰链的最大位移确实要好于传统铰链，但正弦波纹柔性铰链的行程更为可观，是半圆形波纹柔性铰链的2.18倍。由此可见，波纹形铰链在行程方面相比于传统矩形截面以及圆形截面的铰链有很大的优势，同时波纹铰链的行程随着波纹单元的增加，其最大行程也会不断增加。本文所提出的正弦波纹铰链的性能相比于半圆形不仅在x轴向上的位移更佳，而且在y轴方向变形量也同样更具优势，如图4所示，是半圆形的2倍，验证了设想一的合理性，正弦波纹铰链的柔度相比较于半圆形波纹更大。

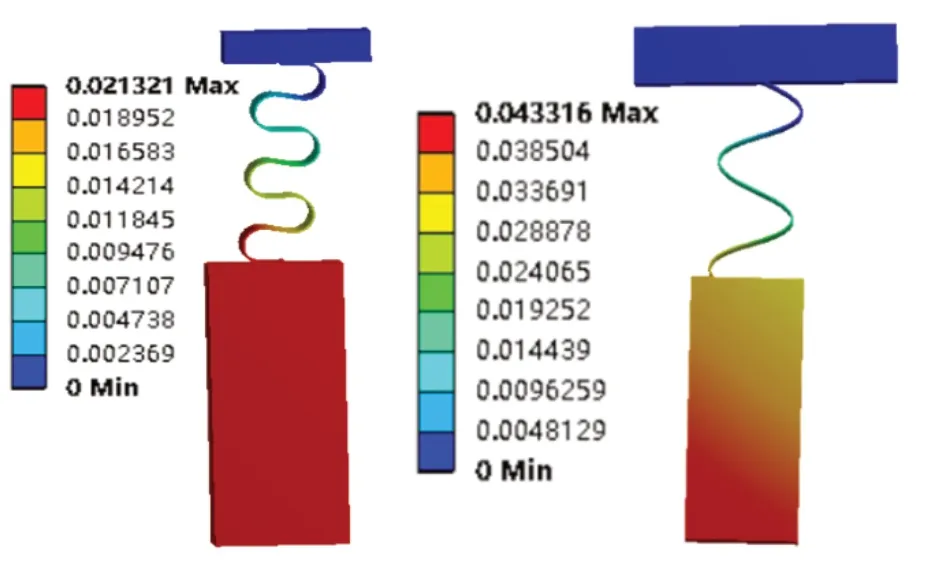
图4 波纹柔性铰链y轴方向位移云图

2.1 双正弦波纹铰链设计分析

虽然相比与图1所示的三角形和矩形周期性悬臂梁拐角的容易产生应力集中的尖锐角，波纹柔性铰链已经有所改善，但是在交变载荷的作用下，等厚波纹铰链在波峰波谷处仍旧容易产生应力集中的现象，而导致疲劳劳损问题。据此，提出设想二：若在保持单元波纹整体侧面面积不变的情况下，将其尺寸进行合理分布，在波峰波谷处适当增加厚度，可以有效改善应力集中的现象。而将正弦曲线上移0.1mm后所形成的双正弦波纹铰链则刚好可以达到相应的效果，单元等距正弦波纹和双正弦波纹的侧界面曲线图分别如图5所示。

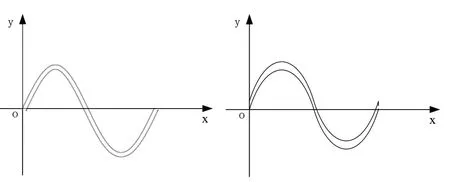
图5 等距正弦与双正弦单元波纹曲线图

由图5可以看出，等距0.1mm和上移0.1mm的正弦曲线所形成的波纹铰链外形有所差异，双正弦波纹铰链的厚度在波纹方向是不断变化的。如图6所示，采用作图法[8]，选取双正弦单元波纹曲线作为作图对象，作y1的切线l1与y1相交于点A(x1，y1)，再作l1的垂线l2交y2于点B(x2，y2)，连接OA和OB，OA与x轴夹角为α，OB与x夹角为β。如式(4)所示，根据投影定理，将三条线段投影于x轴，并采用向量法来表示其厚度的变化情况，通过式(4)、式(5)可以得出厚度AB的变化公式，如式(6)所示。

图6 厚度AB作图示意图

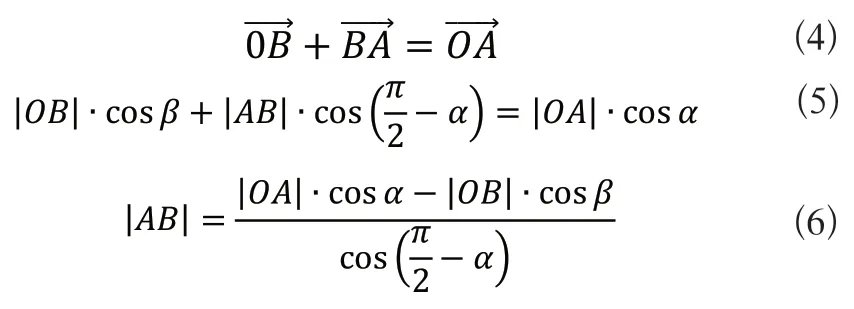
将点A(x1，y1)和点B(x2，y2)坐标代入式(6)，可以得出|AB|的表达式(7)，再联立y1和y2的正弦曲线公式以及式(7)使用MATLAB计算，结合各参数取值范围如式(8)所示，便可以得出双正弦波纹铰链的厚度|AB|的变化曲线图，如图7所示，可以看出，厚度在波峰波谷的时候厚度值达到最高值，并以此建立对应的双正弦波纹铰链模型，对其进行有限元分析验证，是否可以有效减少应力集中的问题。

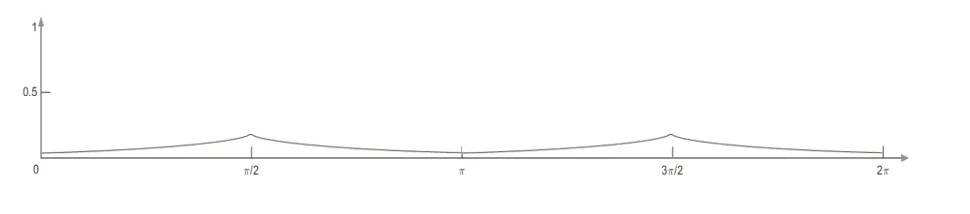
图7 厚度AB变化曲线图

2.2 波纹铰链静力学分析对比验证

在三维软件进行数字建模后，使用ANSYS对这三种波纹铰链进行静力学分析，得出三者在x轴和y轴上的最大行程以及最大应力，仿真结果如表1所示。由表中数据可以看出，等距正弦铰链在x轴和y轴方向的最大位移，都是半圆形铰链的2倍，最大应力则分别是3.4倍和1.5倍。但是在考虑到波纹铰链波峰和波谷的在交变载荷作用下带来应力集中的问题，而采用双正弦铰链使得波纹铰链厚度尺寸得到更合理的分布后，由数据可以直观地看出其优势。双正弦波纹铰链在x轴和y轴方向上的最大位移分别是半圆形的14.8倍和8.9倍，最大应力甚至增加到了15.6倍和3.1倍。通过数据可以清楚地看出，相比于等厚的半圆形和等距正弦铰链，在相同外部作用载荷下，以及同样的材料和空间内，采用双正弦结构的铰链在性能上更具优势，无论是在x轴和y轴的行程上，还是在能承受的最大应力方面，都得到了显著的提高。同时，也验证了先前2.1节中所提出设想二的正确性，合理的尺寸分布确实可以有效提高波纹铰链的性能。

表1 三种波纹铰链有限元分析数据对比表

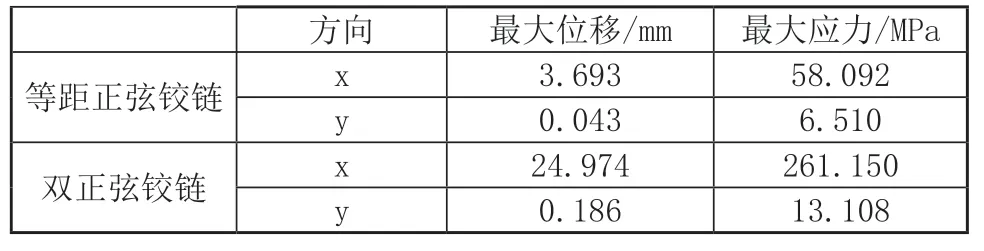
（续）

2.3 双波纹对称结构分析

铰链在外部载荷产生的最大位移是衡量柔性铰链平台的一个重要指标。为进一步验证先前理论的合理性以及实用性，参考王等人将波纹铰链应用于定位平台的方案，本文中选取各波纹的双波纹对称结构来作为试验对象，通过静力学和模态分析对其性能进行对比参照，来分析三者的优劣。通过模拟在相同的作用力下，各波纹结构在x轴和y轴方向上的位移和应力应变情况，半圆形波纹、等距正弦波纹、双正弦波纹铰链的静力学仿真结果依次如图8和图9所示。

图8 x轴方向受力位移及应变云图

图9 y轴方向受力位移及应变云图

根据静力学仿真结果，可以看出在将波纹铰链应用于类似定位平台的环境时，等厚度的半圆形与等距正弦波纹铰链在x轴方向上的位移和应力都相差不大，而在波峰波谷厚度有所变化的双正弦波纹铰链的行程和最大应力都要较大程度上高于等厚波纹铰链，说明合理的尺寸分布，不仅可以改善交变载荷下造成的应力集中现象，同样也可以有效提升波纹铰链在定位平台上的应用性能。相应的，在y轴方向上则可以清楚看出，正弦波纹铰链的最大位移和应力都要高于结构相对紧凑的半圆形波纹铰链，同时也验证了1节中所提到的设想一。由此可见，双正弦波纹在x轴和y轴上的行程和最大应力相比于半圆形波纹铰链皆得到了很大的提升，说明若将其应用于定位平台同样也可以使得定位平台的性能得到一定的提升。

考虑到由于正弦波纹铰链柔度高于半圆形波纹铰链，可能导致正弦铰链会比半圆形铰链更易受外部振动影响，而带来共振问题导致结构破坏的情况。因此，需要对三者进行相应的模态分析，观察其各阶模态下对应的频率变化情况，具体参数如表2所示。

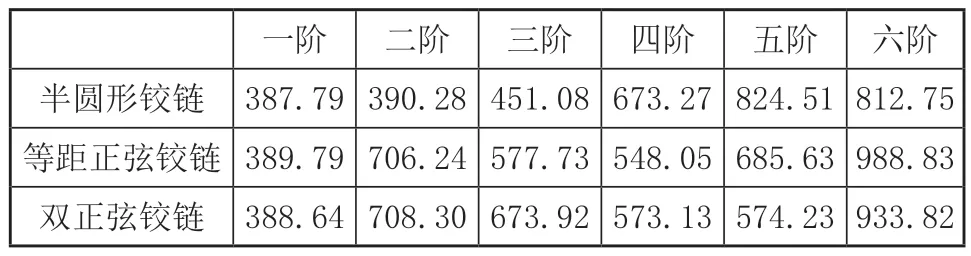
表2 三种波纹铰链各阶模态固有频率（Hz）

模态是结构系统的动力学特性，是系统的固有振动特性，每一阶模态都对应一个特定的固有频率[9]。对三种波纹铰链进行模态分析，可以了解到它们的固有频率范围，可以针对性地避免产生共振而导致损坏。由表2中的数据可以看出，这三种波纹铰链的六阶固有频率范围都相差不大，皆在Hz380～1000Hz之间。对此，也在一定程度上说明，这三类波纹铰链可以用于相类似的工作环境之中。在柔顺铰链的质量(m)和材料为定值时，刚度越小则柔度越大，固有频率也越大。其中，刚度(K)与柔度(δ)以及刚度与固有频率(f)的关系式分别如式(9)和式(10)所示。

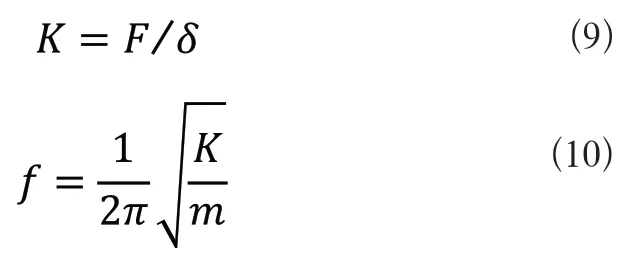
由式(9)和式(10)可看出刚度与柔度成反比关系，固有频率则与刚度也成反比关系。通过联立式(9)和式(10)可以得到固有频率和柔度的关系式，如式(11)所示。

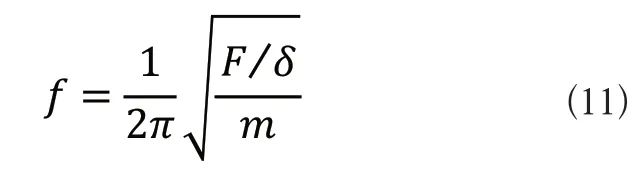
本文中为得到行程更佳的铰链，根据式(11)所示，当固有频率越大则柔度更大，同时，所得铰链的行程也更佳。以平面二自由度定位平台的位移为例，由于一阶和三阶模态分别是在x轴和y轴方向的振波频率，以两者为主要判别依据对双波纹对称结构进行对比分析。从表2数据可以看出，在x轴向上，波纹铰链固有频率大小差距不大，正弦波纹铰链略微大于半圆形铰链，说明x轴方向上正弦铰链的柔度只是略优于半圆形铰链。而在y轴方向上正弦铰链固有频率数值明显要要高于半圆形铰链，且双正弦铰链的数值更佳。综合分析可知，根据式(11)中波纹铰链固有频率和柔度的关系式，结合各阶模态分析的数值可以看出，数值与静力学仿真结果大体一致，说明作为双波纹对称结构应用于定位平台时，双正弦波纹铰链也同样具有一定优势。

3 对比验证

为了更直观地将单波纹和双波纹铰链结构的有限元分析结果进行对比验证，其最大位移、最大应力以及相应的提升率如表3所示。

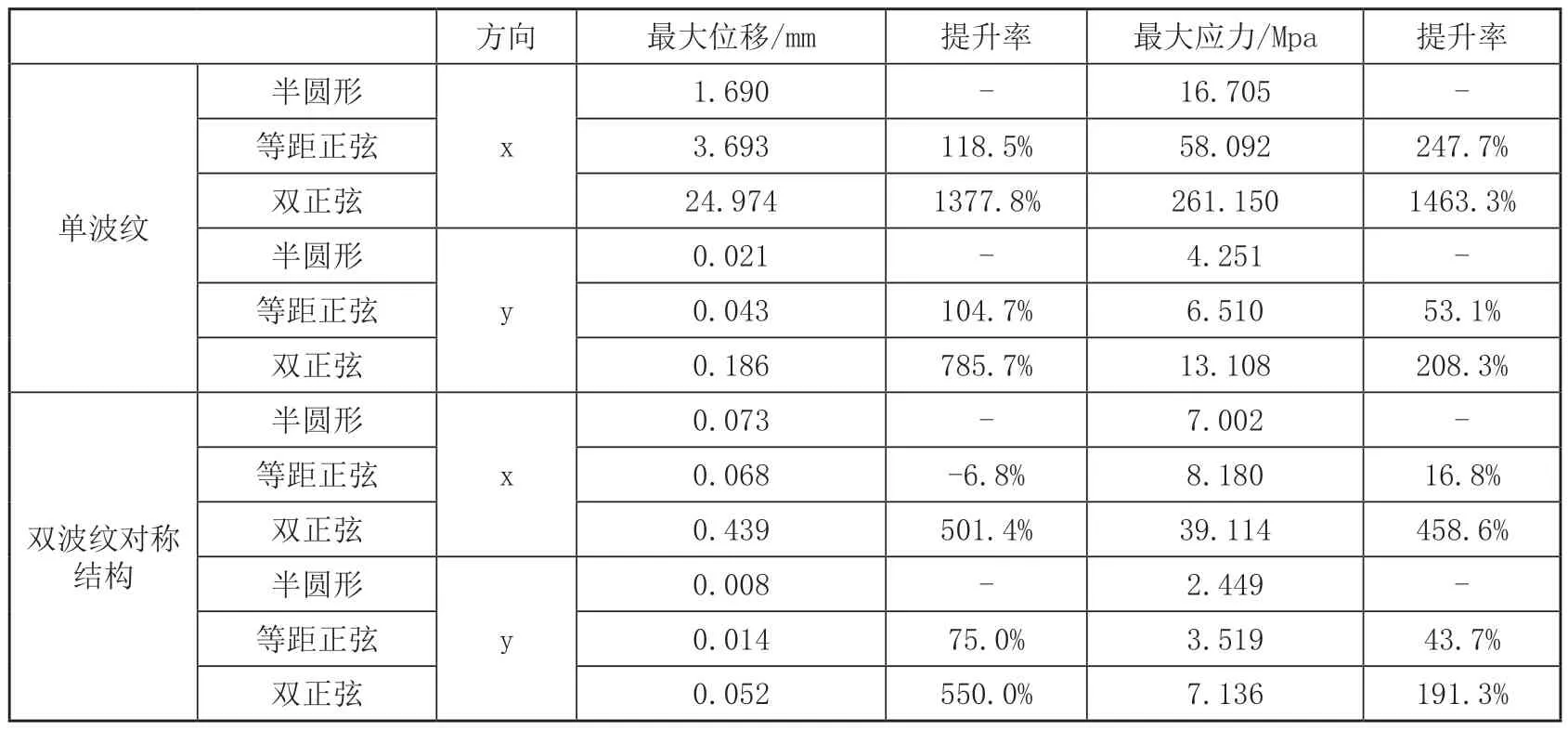
表3 波纹铰链静力学分析结果对比表

从表3中的数据可以看出，对于等距正弦波纹铰链，在单段的结构时，最大位移以及应力方面相比去半圆形铰链提升皆较为显著，而在应用于双波纹对称结构时，可以看出，其在x轴的位移提升效果并不理想，但可以证明正弦铰链相比于半圆形铰链，在y轴位移具有一定的优势，同时也验证了1节中所提出的适当增加每半个单元波纹的距离设想一的正确性。针对于在交变载荷作用下，避免等厚铰链波峰波谷出现应力集中的问题，将其厚度进行合理分布后得到的双正弦铰链，则明显改善了等距正弦波纹铰链的不足之处，无论是在x轴和y轴的位移方面还是在最大应力方面，性能都得到了巨大的提升，有效证实了2.1节中所提出设想二的正确性。

4 结语

1）提出了一种基于双正弦曲线的波纹铰链设计，根据投影定理采用向量法计算出波纹铰链厚度的变化情况，通过实例仿真分析验证了正弦波纹铰链理论分析的正确性。

2）将半圆形、等距正弦波纹铰链与双正弦波纹铰链的单段波纹，以及根据定位平台而设计的双波纹对称结构，进行性能对比。结果表明，在y轴行程上，正弦波纹铰链明显优于半圆形铰链；在x轴行程上，双正弦波纹铰链有效改善了波峰波谷会出现的应力集中问题，进行合理尺寸分布后的性能显著提高。这也充分表明了双正弦波纹铰链结构设计的合理性与有效性。

3）由于本文中的同尺寸双正弦铰链参数受到人为设定的影响，若对曲线的参数a、b、c、d进行优化设计，所得的波纹铰链效果会更加。同时也可以尝试不同尺寸的正弦曲线组合来进行优化设计，为波纹铰链设计提供了一定的研究思路。