基于地球坐标系的全球惯性导航与组合导航方法

王鑫耀, 王双甲, 何梓君, 李荣冰*

(1.南京航空航天大学 导航研究中心，江苏 南京 211106； 2.航空工业西安飞行自动控制研究所，陕西 西安 710065；3.空装驻南京地区第四军事代表室，江苏 南京 210012)

极区导航是实现全球导航的重要组成部分，具备极区导航能力的现代飞机在全球航行中能突破航线规划的制约，针对特定的飞行任务，若能够飞跃极区则可以节省燃料和飞行时间，提升任务效率并增加经济效益。

飞机在极区航行时，航行环境与常规地区有显著不同。受极区特殊的自然环境影响，卫星导航、天文导航在极区面临性能降低的问题，地磁导航、地形匹配导航则几乎不可用。因此，面对极区特殊的航行环境，惯性导航系统不依赖外部信息的特性使其成为完成极区导航任务的主要导航系统。然而由于极区经线收敛并最终汇聚于一点，极点处北向无定义，地理坐标系失效，常规的指北方位惯导算法在极区存在计算溢出和误差放大等问题，因此在极区不适用。

格网导航是解决极区导航问题的有效方法，但根据其机械编排，格网导航在赤道附近无法使用，不具备独立完成全球导航任务的能力。如果采用指北算法和格网算法切换的全球导航方案，则2种机械编排的切换将使惯导算法无法统一，增加了算法的复杂性和工程实现的难度。

针对全球导航问题，文献[1]提出了法向量的方法;文献[2]研究了在通用的地心地固坐标系(Earth-Centered Earth-Fixed,ECEF)下的惯导机械编排，但导航参数的输出仍在地球系下，物理意义不明确，不适用于近地导航。文献[3]和文献[4]阐述了完整的全球惯性导航算法。其中，文献[3]提出了以游移方位惯导编排为内核的间接格网惯性导航算法；文献[4]研究了基于伪地球坐标系的全球导航算法，但均没有考虑惯导误差累积的问题。文献[5]和文献[6]研究了基于地球系的惯性/卫星组合导航方法，均采用了松组合模式且没有对导航参数如何输出进行阐述。

为实现全球导航中惯性导航算法的统一，本文阐述了基于地球坐标系的全球惯性导航方法，并通过方向余弦矩阵将导航参数转换至地理坐标系和格网坐标系,实现了导航参数的有效输出。针对长航时惯性导航系统存在的误差累积的问题，设计了基于地球坐标系的惯性/卫星紧组合导航滤波器，有效提升了导航精度。

1 基于地球坐标系的惯导机械编排

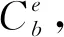
(1)

(2)

由比力方程可得地球坐标系下的速度微分方程为

(3)

由于经线在极点收敛，极点处经度无法表示，因此地球坐标系系下的位置用直角坐标表示为Re=[xyz]T，位置微分方程为

(4)

根据地球系惯导算法的机械编排，计算原理框图如图1所示。

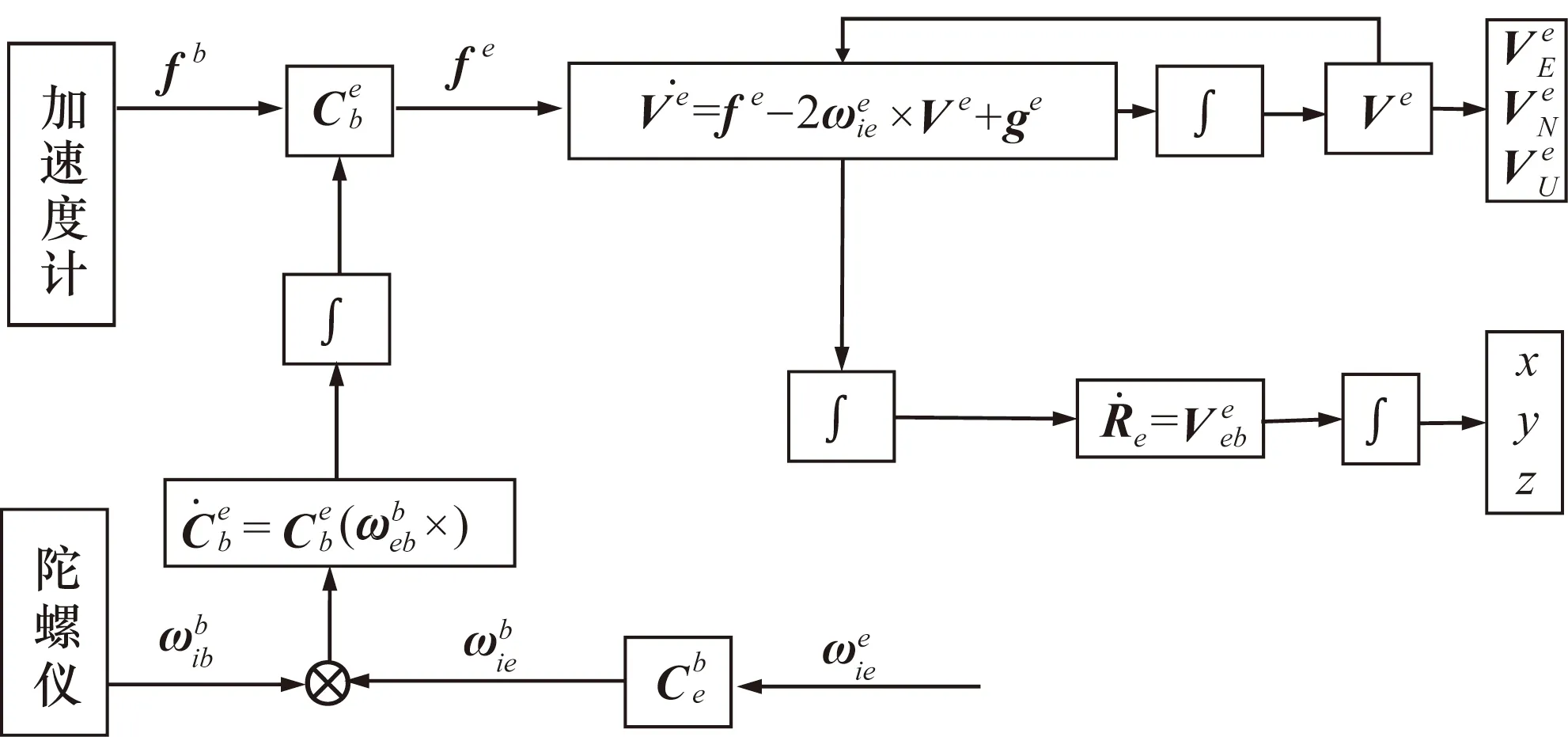
图1 地球系惯导算法机械编排

分析基于地球坐标系的惯导机械编排可知，地球系的惯导算法采用地球坐标系为导航坐标系，与飞机位置无关，不存在导航坐标系在极区失效的问题。在导航解算过程中随着纬度的升高，直至到达极点附近，不存在趋于无穷大的计算项，避免了指北算法导航解算过程中误差放大和溢出的问题。采用直角坐标表示位置，避免了在极点附近输出位置时经纬度表示位置产生的误差放大和奇异的问题。与格网算法相比，基于地球系的惯导算法力学编排更简洁，计算量更小，且适用于全球导航。

2 基于地球坐标系的导航参数输出

在全球导航任务中，基于地球系的惯导算法能在全球范围内完成导航解算，不需要进行机械编排的切换，且相比于指北算法和格网算法计算量更小。但是地球系下的导航参数物理意义不明确，适用于内部解算但不适合对外输出。因此考虑将基于地球系的惯导算法作为全球导航解算的内核，面对需要导航参数输出的应用场景，则将参数转换至地理坐标系或格网坐标系输出。

中低纬度地区导航参数通常在地理坐标系下输出；在高纬度地区，随着纬度升高经线收敛，地理系下导航参数的误差增大，在极点处地理系将失效，失去航向参考导致航向角无法表示。而格网坐标系以格林尼治子午线作为参考航向则可以避免导航坐标系在极区的失效，且格网航向在格网系输出时误差不发散。地球坐标系与地理坐标系、格网坐标系的关系如图2所示。

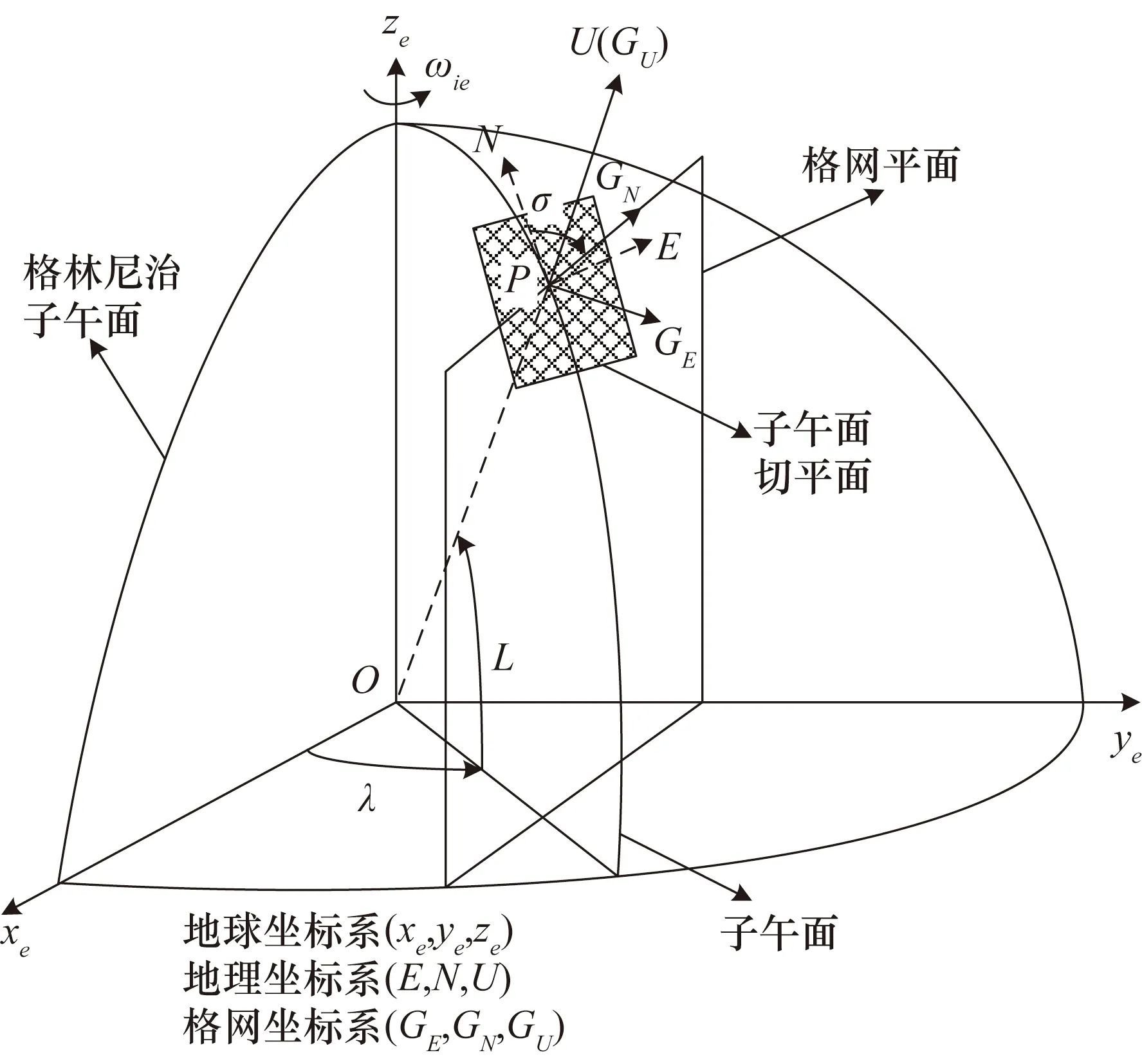
图2 地球系与地理系、格网系的关系

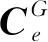
(5)

(6)

式中：λ为飞机经度；L为飞机纬度。

(7)

根据姿态阵可以得到格网系和地理系下飞机的姿态角。

地球系下的速度转换至格网系和地理系表示为

(8)

基于地球坐标系的全球导航方法分离了惯导解算和参数输出过程，其机械编排在地球坐标系下进行，实现了全球范围内的统一，导航参数根据所处的纬度位置选择在地理坐标系或格网坐标系下计算输出。

对于卫星导航系统，通常以地球坐标系为导航坐标系，与本文的惯导机械编排一致，其输出的地球系下的导航参数同样可以通过方向余弦矩阵转换至地理系或格网系，与惯导的数据进行对比验证。

3 全球紧组合导航滤波器设计

基于地球坐标系的全球导航方法在极区应用中解决了导航系失效、计算误差放大和溢出等问题，但无法避免惯性导航算法的固有特性，即系统误差随时间不断累积，在长航时的任务中无法满足系统精度要求，因此需要借助其他导航技术辅助惯性导航，通过组合导航修正系统误差。

随着北斗三号系统的建成，北斗在极区的信号质量和定位服务性能获得了显著提升，本节研究了极区惯性/卫星紧组合导航算法，以地球坐标系为导航坐标系，与惯性导航系统进行组合，并采用伪距组合的紧组合模式，紧组合的导航模式相比松组合具有更高的导航精度和鲁棒性[8]。

全球紧组合导航系统总体架构如图3所示，其中惯导解算与紧组合导航在地球系下进行，导航输出在地理系与格网系下进行。

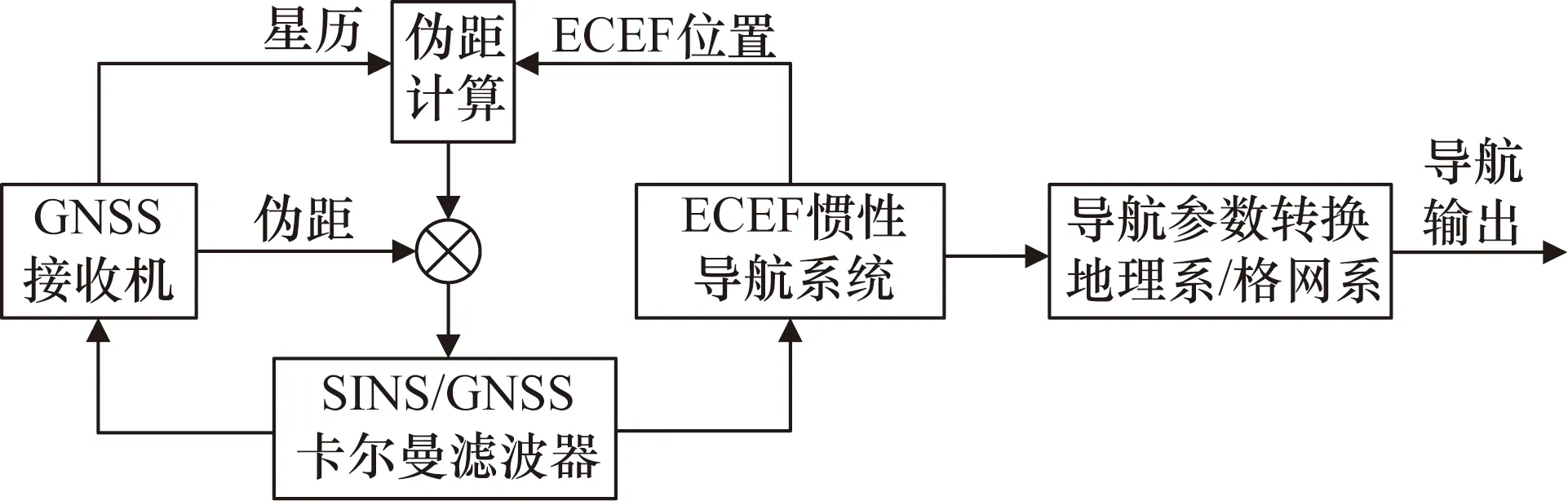
图3 全球紧组合导航系统总体架构

3.1 系统状态方程

卡尔曼滤波的状态方程为

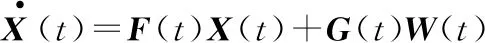
(9)

式中:F(t)为系统转移矩阵;G(t)为系统噪声矩阵;W(t)为系统噪声。

滤波器状态向量的INS部分包括15个状态：

(10)

分别为地球系下的姿态、速度、位置误差以及陀螺仪和加速度计误差。

地球系下的姿态、速度和位置误差方程[7]为

(11)

(12)

INS部分的系统矩阵为

(13)

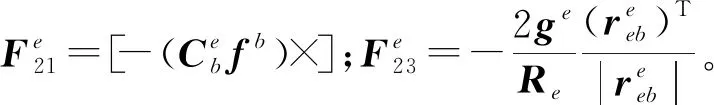
系统噪声向量WINS(t)为陀螺仪和加速度计随机噪声:

(14)

系统噪声分布矩阵G(t)为

(15)

(16)

系统矩阵、系统噪声和噪声分布矩阵分别为

(17)

合并INS与GNSS状态方程，得到系统状态方程为

(18)

3.2 系统量测方程

系统量测量为伪距，伪距量测方程为

Zρ(t)=Hρ(t)X(t)+Vρ(t)

(19)

(20)

式中：(xu,yu,zu)为接收机在地球坐标系下的位置；(xsi,ysi,zsi)为第i颗可见星的位置；ρi为接收机到第i颗可见星的距离。

笔者基于卡尔曼滤波构建了地球系下的惯性/卫星紧组合导航滤波器，相比于常规的地理系下的松组合导航，适应了极区导航的需要，具备全球导航能力，且紧组合模式相比松组合具有更高的滤波精度。

4 基于地球坐标系的全球导航算法仿真

针对一定精度条件的惯性器件，对地球坐标系的全球惯性导航算法和紧组合导航算法进行仿真验证。本次仿真利用航迹发生器产生飞行器航线上对应的飞行数据，并以该飞行数据为基础，通过IMU仿真子系统仿真产生惯性导航系统所需要的相关数据。同时，针对典型的惯性传感器的精度特性，加入系统误差，对算法进行仿真。

4.1 仿真条件设置

仿真航迹设置如表1所示，飞机沿经线向北匀速飞行，飞行过程保持水平直线巡航。其中航迹1从高纬度地区出发并飞跃极点，航迹2始终在中低纬度地区。

表1 仿真航迹设置

基于生成的航迹利用数值解法反推可以得到理想的IMU数据，通过加入器件误差仿真实际的IMU输出。参考典型的惯性基准系统精度水平，设置惯性器件误差参数如表2所示。

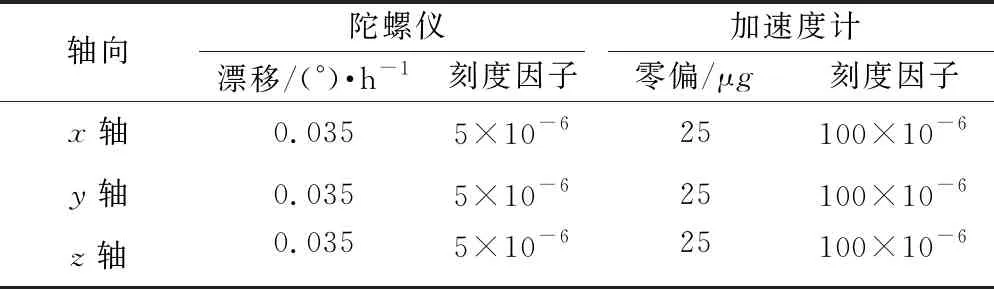
表2 惯性器件误差参数设置

4.2 惯导系统仿真

首先对基于地球坐标系的惯导算法进行仿真，航迹1位于极区内，将地球系算法的仿真结果与格网算法进行对比的仿真结果分别如图4和图5所示，位置误差在地球坐标系下表示，姿态角误差在格网系下表示，航向为格网航向。

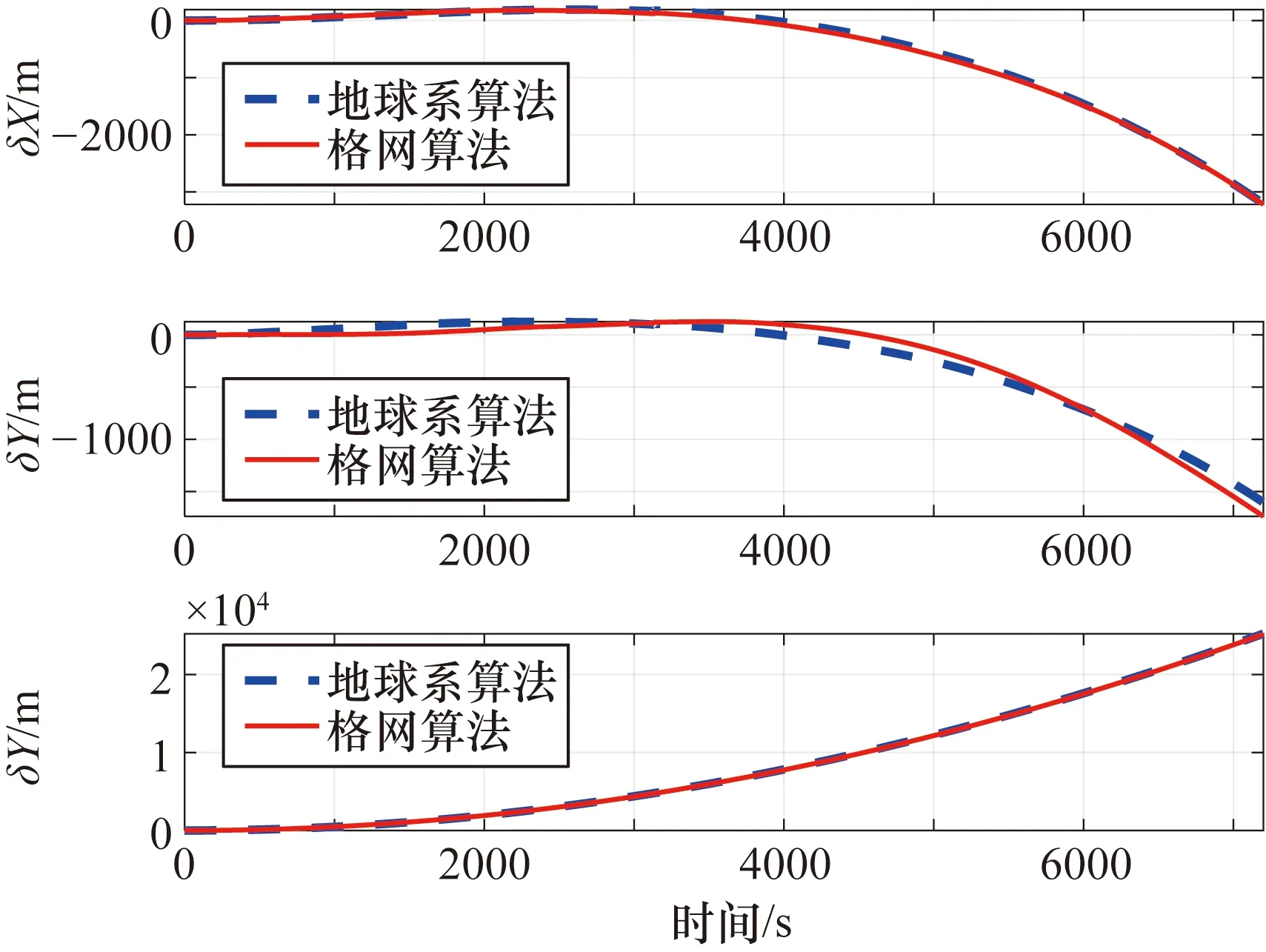
图4 航迹1算法位置误差仿真对比

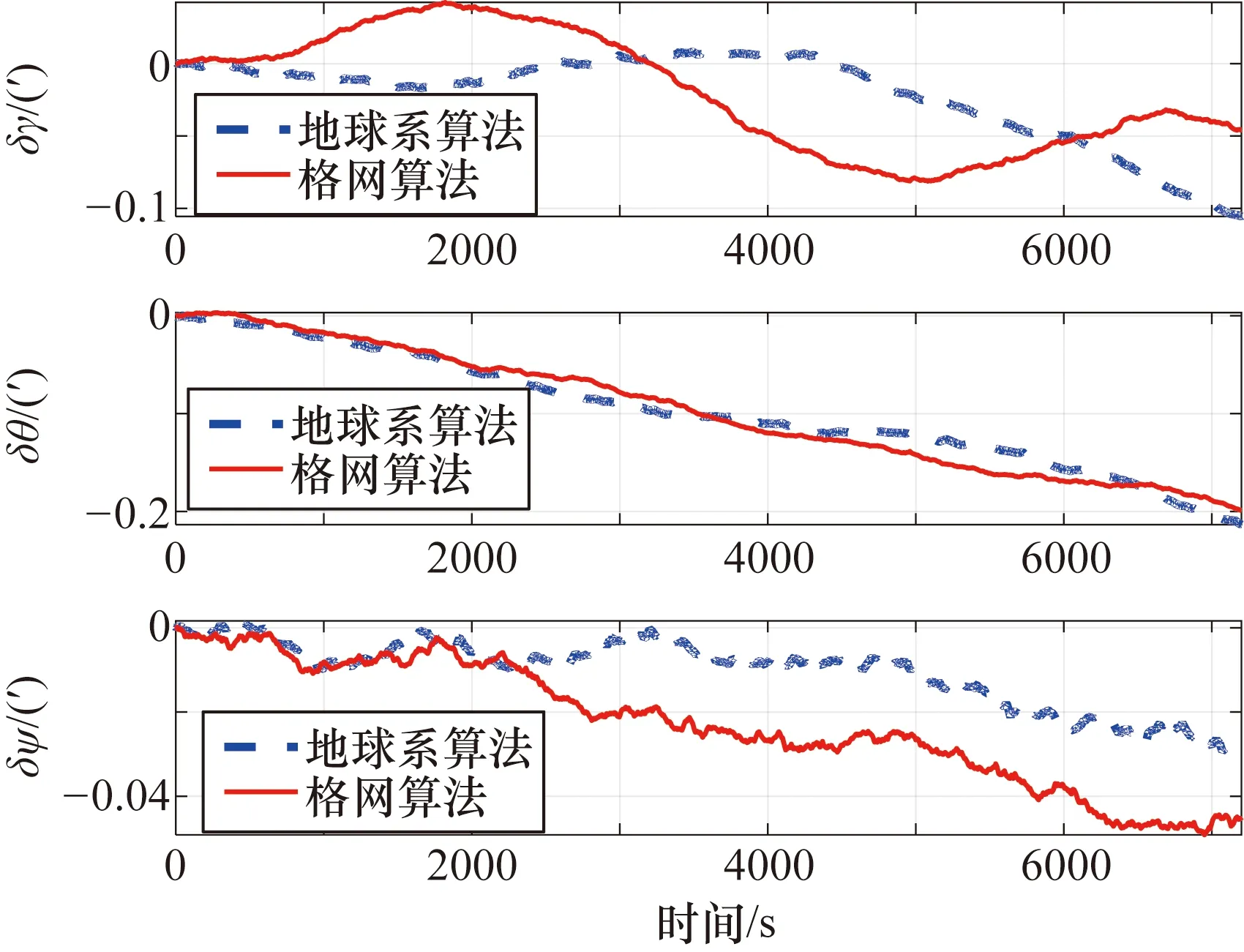
图5 航迹1姿态角误差仿真对比

航迹2位于中低纬度地区，将地球系算法的仿真结果与指北算法进行对比的仿真结果分别如图6和图7所示，位置误差在地球坐标系下表示，姿态角误差在地理系下表示。

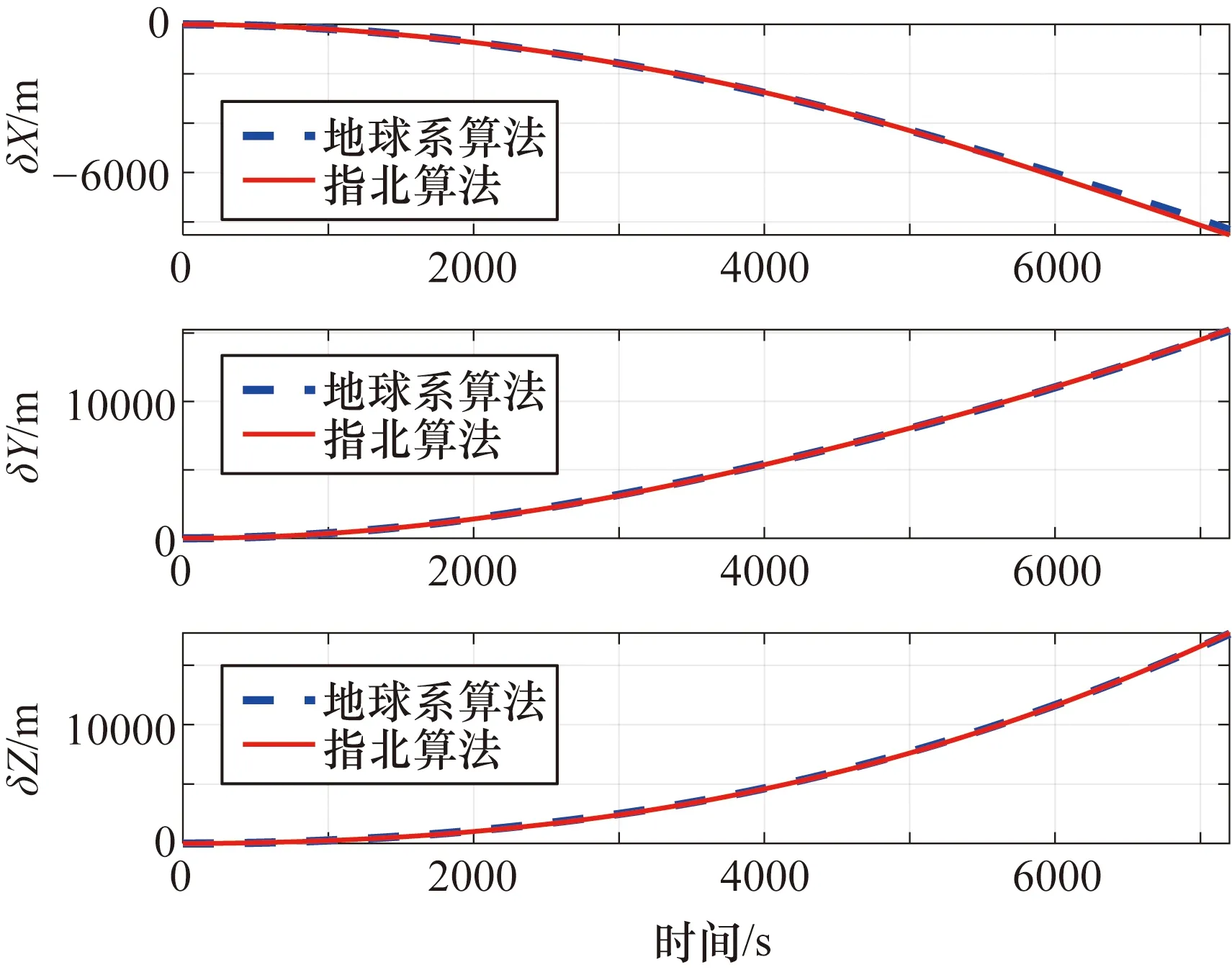
图6 航迹2算法位置误差仿真对比

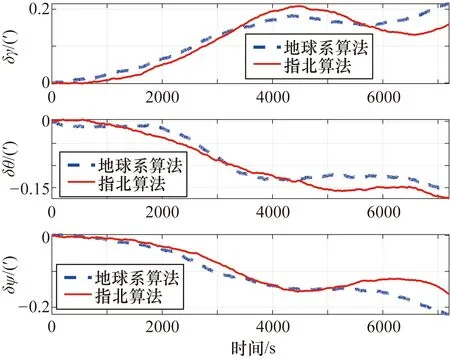
图7 航迹2姿态角误差仿真对比

分析仿真结果可知，基于所选的惯性传感器精度水平，所实现的全球惯性导航算法在极区与非极区的性能分别与格网算法和指北算法的性能一致，验证了全球惯性导航算法的有效性。

4.3 紧组合系统仿真

由于惯性导航系统的固有特性，在长航时的航行中系统存在误差累积问题，如4.2节仿真结果所示，系统的位置误差出现较大偏差。本文利用卫星辅助惯性导航系统，构建紧组合导航系统抑制误差累积。

设置仿真卫星可见星数为10颗，位置精度因子(Position Dilution of Precision,PDOP)在2左右，伪距量测误差为7 m，白噪声为2 m。紧组合导航系统在极区与非极区的位置误差分别如图8和图9所示。

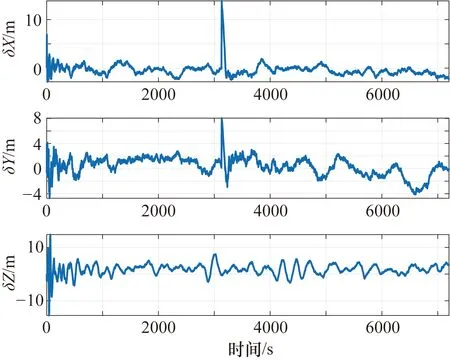
图8 紧组合导航系统航迹1位置误差

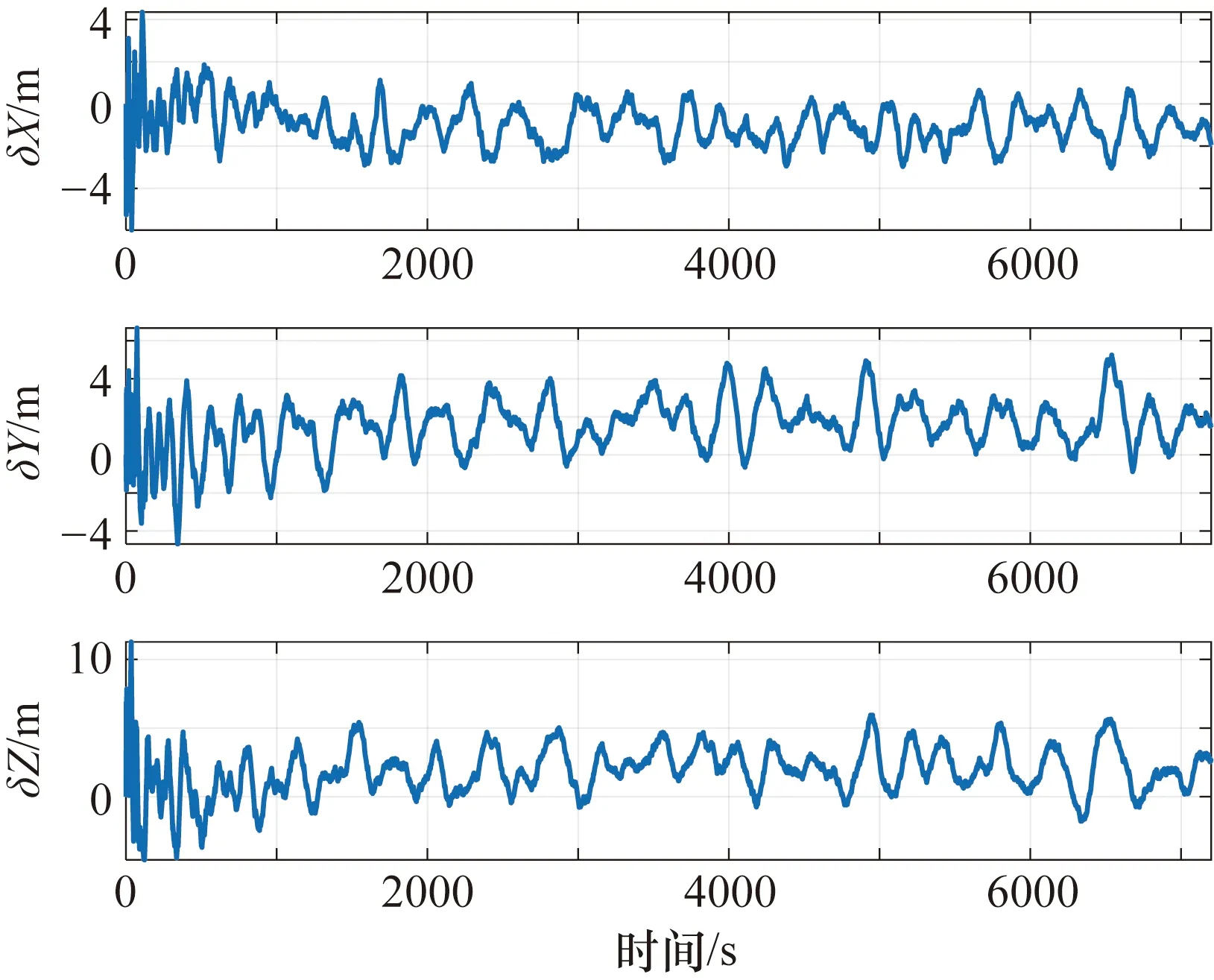
图9 紧组合导航系统航迹2位置误差

由仿真结果可知，紧组合导航模式下系统的位置误差明显减小且没有出现发散，导航性能明显改善，仿真结果验证了紧组合对于抑制惯导误差累积的有效性。

5 结束语

为实现惯导系统的全球导航，研究了基于地球坐标系的全球导航方法，将惯导系统的实现分为内在的机械编排和外在的参数输出2个部分，实现了全球范围内机械编排的统一和导航参数的有效输出。针对长航时惯导系统误差累积的问题，设计了惯性/卫星紧组合导航滤波器，有效提升了导航系统精度。

通过仿真对基于地球坐标系的惯导系统和紧组合导航系统的性能进行了分析。结果表明，全球惯性导航算法在极区与非极区的性能分别与格网算法和指北算法的性能一致，紧组合导航系统有效抑制了惯导误差累积，提升了定位精度。