角平分线教学中渗透深度学习

郭海燕

摘要：深度学习指导，互动白板技术的支持融合下《线段垂直平分线》教学实践的应用.

关键词：理解迁移新知识生成;类比构建知识体系

一、理解迁移新知识生成

人教版教材中 “线段垂直平分线”内容安排在“角的平分线”之后，两者的教学内容与顺序均以概念认识、性质探究、判定探究、应用实践为主线。

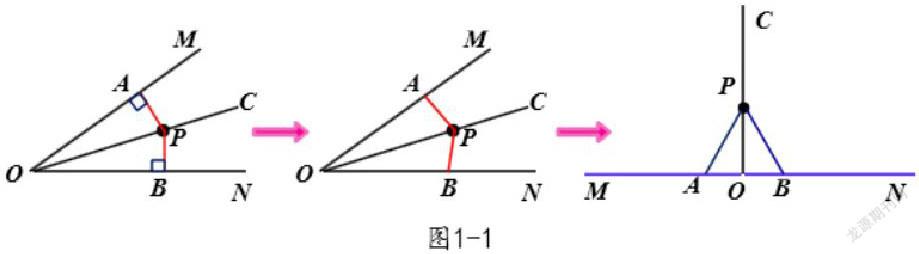
若把“角的平分线上的点到角的两边的距离相等”这个定理中的“到角的两边的距离”衍化为“角的平分线上的点到角的两边与顶点等距离的点的距离相等”;再把角度大小一般化，展成平角，结论依然成立（如图1-1）。

此时，角的平分线所在直线就是平角两边所在直线的垂线，也是与顶点等距离的点所构成线段的垂直平分线，原有的结论依然成立，实质上就是线段的垂直平分线的性质。再结合八年级学段学情与教学目标，从数学的眼光看在对待问题上，学生已经具备抽象意识了，数学思维已经从小学学段的推理意识形成逐步转向推理能力的形成过程当中，渐渐向发展逻辑思维能力迈进的时候。因此，笔者认为“线段的垂直平分线”的学习，完全可以从“角的平分线”切入，借助信息技术支持的几何直观，实现研究方法的有效迁移，依合理、逻辑条理的，从当前内容向纵深、一般化推广，然后再联想所学的内容跟后续学习的什么内容相关，进而完成新知识生成，丰富认知策略，学会“类比迁移”。设计成下列问题驱动完成操作：

案例：

角平分线的性质：角的平分线上的点到角的两边的距离相等

问题1：已知：如图1-2，∠MOC=∠NOC，点P在射线OC上，PA⊥OM于A，PB⊥OM于B. 求证：PA=PB

问题2：已知：如图1-3，∠MOC=∠NOC，点P在射线OC上，AO=BO. 求证：PA=PB

问题3：已知：如图1-4，∠MON=180o，∠MOC=∠NOC，点P在射线OC上，AO=BO. 求证：PA=PB

问题4：已知：如图1-5，∠MON=180o，∠MOC=∠NOC，点P在直线OC上，AO=BO. 求证：PA=PB

问题5：已知：如图1-6，直线OC⊥线段AB于O，AO=BO，点P在直线OC上. 求证：PA=PB

归纳：线段垂直平分线上的点和这条线段两个端点的距离相等---线段垂直平分线的性质

这个设计的意图在于：“线段垂直平分线的性质”定理由“角的平分线的性质”定理纵深推广迁移而得，不是按照老师要求被动操作的，而是需要学生跳一跳才能摘到的果实，思维量大，探究味浓，故而，参与性强，特别是这种纵深推广、特殊化类比比较的思维方式，是一种深层次的迁移，贴切的体现了深度学习要求学生“积极投入，处于较高认知水平层次、基于理解”的学习过程，已有的背景下生成新知识，逐渐完善知识结构，“构建自己的知识体系”，同时“解决情境下问题”。完成这个学习过程是在互动白板技术支持下，“角的平分线”从一般化的角，展成平角，再特殊化成“线段的垂直平分线”，把设计的情景图以及操作在互动白板的技术支持下一一动态呈现，其直观性对完善学生的认知方式和提高数学学科核心素养能力均有深远的影响。

二、类比构建知识体系

学习角平分线的判定时，我们是这样进行：我们知道，角平分线上的点到角的兩边的距离相等。问题：交换角的平分线性质中的条件和结论，你能得到什么命题，这个新命题正确吗？

去探究，证明得到的结论是肯定的：到角的两边的距离相等的点在角的平分线上类似的，学习线段的垂直平分线的判定时，同样类比的问题：交换线段的垂直平分线的性质中的条件和结论，你能得到什么命题，这个新命题正确吗？

在得出“线段的垂直平分线性质”后，教材便指出，性质定理条件与结论互换也成立，但没有直接证明，以小贴士的形式问“自己证明吗”？配套的教师用书中要求学生自己给出证明，经历完整过程，感受证明的必要性。这与学习“角的平分线的性质”时要求相同，所以类比“角的平分线的性质定理的逆定理”，笔者设计如下问题串：

问题1：在性质定理探究结束后，下一步同学们想研究什么？

问题2：性质定理的逆命题是什么？

问题3：这个逆命题是真命题吗？如何证明？

这个设计的意图在于，引导学生类比角的平分线的学习，联想到研究性质定理是否也有逆定理？同时，教学中引导学生逐步完善命题的规范表述，实际包含一个条件“与线段两个端点距离相等”，两个结论“点在这条线段的垂直平分线上----该点既在此线段的垂线上又在此线段的平分线上”，如何实现“点既在垂线上又在平分线上”？通过白板实验反例驱动学生思考，得出：过这点垂直线段的垂足会是线段中点，线段中点与这点连线会垂直此线段。理解后归纳这类问题处理通法：通过作辅助线实现一个结论，证明剩下一个结论。

正如数学家德海纳特说，所有有活力的思想都有一个缓慢的发展过程，应留足够的探索时间，引导学生深度学习，领悟定理发现或发展、问题解决过程有着不可忽视的教育价值.

参考文献：

[1]郭华.深度学习及其意义[J].课程·教材·教法，2014（4）.

[2]刘华为，沈旭东.基于操作感悟突出生成过程---“三角形有关概念的几点思考”[J].中学数学教学参考（中旬），2020（1-2）.

基金项目：福州市教育科学研究“十三五”规划2020年度课题《基于深度学习的数学教学案例探究----以互动白板在数学教学中的实践为例》 编号：（FZ2020GH020）ED38FE8A-F21C-44D5-AB38-7734EE5A08DF