面向酒坛抓取的仿生机械手的结构设计与分析

王俊强，管声启，李振浩，于资江，王静国，刘文慧

(1.西安工程大学机电工程学院，陕西 西安 710048；2.绍兴市柯桥区西纺纺织产业创新研究院，浙江 绍兴 312030)

0 引言

黄酒是世界三大酿造酒之一，其生产酿造技术独树一帜，其中以浙江绍兴黄酒为典型代表[1]。近年来，黄酒产业随着经济的增长在不断扩大，但是由于黄酒生产中人力资源消耗大，机械自动化水平低等，导致企业劳动强度大、无法适应全自动化生产，使得黄酒行业的发展受到了约束[2-3]。因此，需要开展“机器换人”技术革新，推进行业向标准化、智能化方向转变[4]。

目前大多数末端执行器多为单自由度，其抓取方式多使用夹钳式，只能实现特定抓取动作，很难实现对力的精确控制。由于传统黄酒的酿造存储多以陶坛为主，陶坛的尺寸各异，且在轴心方向上不对称，用传统的机械手无法实现稳定的抓取。

而人手经过长期进化，能够实现多种抓取动作。加拿大公司研制的SARAH机械手[5]、意大利研发的Smart机械手[6]和RTRⅡ[7]机械手虽具有人手的多自由度，但由于尺寸和控制等因素难以应用实际；斯坦福大学研发的Stanford/JPL机械手[8]，采用绳轮机构，通过传感器进行检测与控制。国内的仿生学末端执行器也取得一定的进展[9]，上海交通大学研究的假肢手SJU-5，能够实现对日常物品的抓取[10]；哈尔滨工业大学研制的HIT-DLR机械手采用5个模块化的手指[11]；清华大学研制的TH型机械手，采用欠驱动原理，具有良好的抓取性能[12]。虽然仿生型末端执行器的性能逐步完善，但依旧存在结构复杂，控制难度大，稳定效果不佳等问题，且由于酒坛体积和形状的限制，难以满足其抓取需求。

本文采用仿生学设计原理，以人手抓取操作为基础，设计一种欠驱动仿生型末端执行器实现对酒坛的抓取操作。

1 仿生机械手结构设计

1.1 整体结构

机械手整体采用三指三指节九自由度的结构形式，主要包含手指和基座2个模块，如图1所示。每根手指模拟人手构型采用近指节、中指节、远指节等三指节结构设计，内部采用特殊绳轮布局的腱传动驱动方式，并且采用独立电机驱动控制方式。考虑到抓取对象的外形尺寸的特殊性，3根手指采用模块化的设计思想，采用空间交错抓取方式，3个手指呈三角形分布方式，单根手指独立分布，其他2个手指基于抓取对象的质心位置并列对称分布两侧，使得各手指中心有足够大的抓取空间，能够满足抓取对象不同尺寸的抓取要求。该种布局及抓取方式可以针对不同的抓取对象，具有自适应性强、抓取范围广等特点。

图1 机械手整体结构

机械手在抓取过程中，3个手指的协调运动是由电机和腱绳通过滑轮以及指腹上的触觉传感器共同完成的。这一动作的完成是通过运动控制模块统一协调分配，而其各个手指又分别由各自对应的电机进行驱动控制，所以运动控制模块在对每个电机控制信号的输入过程中需进行精密的监测和计算，以此来保障整个抓取运动的平稳性。该仿生型机械手的设计综合考虑抓取系统的稳定性和力的平衡因素，在后续的仿真实验部分对驱动手指运动的电机参数设定上保持了统一性，同时在指节间控制运动的弹簧参数设定上进行了差别拟合设定法，这样既有利于保障3个手指在完成抓取动作时的一致性，又使得在完成抓取动作时机械手整体上力的平衡性与稳定性。因此，该机械手在抓取时能够满足欠驱动机械手仿生型原理和自适应抓取设计要求，符合人手抓取机理及实际生产抓取需要。

1.2 工作机理

三指三指节机械手采用模块化设计，每根手指内部均采用相同的绳轮布局。各指节间采用连接轴进行连接固定，并通过多种不同尺寸的滑轮组限定腱绳的缠绕路径，一方面保证各指节间力传递的一致性，另一方面提高手指抓取效率，同时在抓取过程中配合各指节间的扭簧，既可以避免机械手在受力之后状态突变保障抓取的稳定性，又可以使得机械手抓取完成后电机反转，在扭簧的作用力下回弹至初始状态。

机械手内部采用绳轮结合的传动方式，绳轮在对目标实施抓取时，主要应用的是包络抓取的方法原理。由于腱绳在长期使用过程中会出现松弛现象，影响机械手抓取的精确性，通过对现有绳轮传动的多种方式进行分析，采用如图2所示的绕线方式进行设计。其腱绳的具体绕法如下：将腱绳的一端通过紧定螺钉固定连接在远指节的指尖位置处，另一端绕过张紧轮，从远指节与中指节中间连接的大滑轮1下方绕过，到达中指节上的导向轮组1的上方；从中指节与近指节连接处的大滑轮2下方绕过，经由近指节上方的导向轮组2的上方，绕过近指节与基座连接处的大滑轮3，最终将腱绳固定缠绕在驱动电机的绕线轮上。

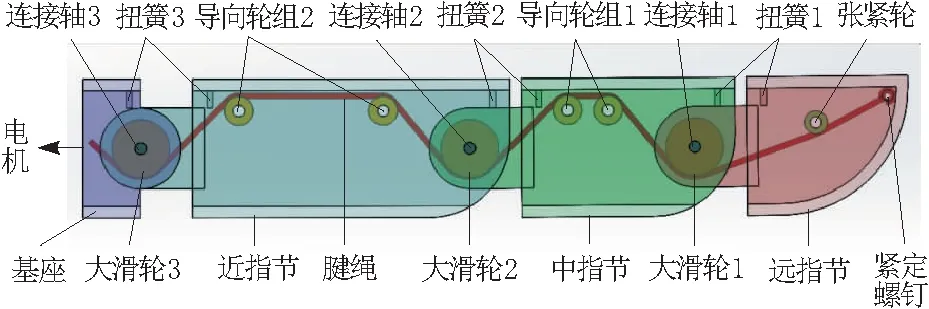
图2 机械手工作机理

在整个手指工作的过程中，当驱动电机开始旋转时，其上的绕线轮也相应的跟着旋转，腱绳开始张紧并收缩。各指节间装有回弹装置弹簧，若不考虑腱绳与各个滑轮之间摩擦力的存在，可以认为在同一根腱绳上的力是处处相等的。随着电机不断缠绕着腱绳，在机械手没有接触到酒坛之前，电机旋转的角度与手指各关节的转动角度值、各指节连接处的滑轮尺寸大小以及指节连接处扭簧刚度在腱绳上的力有关，并按照一定的运动规律开始运动，直至机械手指完全接触到酒坛表面，最后到达其工作极限位置，电机工作停止，机械手完成包络抓取任务。当完成抓取工作后，电机开始反转并释放缠绕在绕线轮上的腱绳，随着腱绳的松弛，在扭簧回弹力和机械手上物理极限位置的共同作用下，手指的各指节逐渐恢复到初始抓取位置处，等待下一次的抓取任务。

1.3 抓取方式

欠驱动仿生机械手采用仿生学原理，采用三指三指节结构设计，绳轮结合的传动方式，模拟人手构造完成对酒坛的抓取搬运工作，如图3所示。三根手指的布局依据酒坛的特殊构造，依据质心点进行对称分布，能够像人手一样针对多种类型的抓取对象以及不同尺寸和质量的物品实现自适应稳定抓取操作。同时，该机械手可以根据不同的抓取任务进行迁移，配合不同工况和任务的机械臂配套使用，可根据抓取对象设置单指抓取、两指抓取和三指抓取等3种不同的机械手工作状态，同时可以根据抓取对象的尺寸大小选择指尖捏取和包络抓取2种不同的工作模式。在一定程度上，能够满足多类型自适应抓取方式。

图3 机械手抓取方式

2 运动学分析

2.1 正运动学分析

为确定机械手各指节运动的位置参数，需要求解机械手在空间中的位姿，这就需要建立指尖和关节运动之间对应的关系，而应用最广泛的方法则是D-H参数法。

本文所设计的机械手采用模块化设计思想，三根手指结构原理相同，并依据人手构造原理及运动特性，采用D-H参数法对单根手指各指节建立坐标系，如图4所示，oxyz为初始状态的全局坐标系，x1y1z1、x2y2z2和x3y3z3为基于手指关节运动变化的动态的参考坐标系。

图4 机械手单根手指坐标系

以全局坐标原点为起点，按照各指节顺序，定义指节长度为li，指节间的转角为θi，指节间的扭角为αi，2个指节间的距离为di。根据所建立的坐标系，列出其对应的D-H参数表，如表1所示。

表1 机械手单根手指D-H参数

欠驱动仿生机械手指尖位置关系相对于全局坐标系的位姿矩阵T为

T=A1×A2×A3

(1)

A1、A2、A3分别为近指节、中指节、远指节等相邻两坐标系之间的齐次变换矩阵。其对应的各齐次变换矩阵分别为：

(2)

(3)

(4)

由式(1)、式(2)、式(3)和式(4)可得

(5)

其中，si=sinθi；ci=cosθi；sij=sin(θi+θj)；cij=cos(θi+θj)；i、j=1，2，3。

所以，指尖位置矢量为

(6)

机械手指尖位置在全局坐标系中的坐标为:

x=l3c1c23+l2c1c2+l1c1

(7)

y=l3s1c23+l2s1c2+l1s1

(8)

z=l3s23+l2s2

(9)

机械手完成抓取动作时，若各指节转角θi已知，则可求解任意状态下机械手指尖位置坐标点，为后续的抓取工作提供理论依据，实现精确控制。

2.2 逆运动学分析

欠驱动仿生机械手的逆运动学即是正运动学的逆，是在已知机械手指尖的运动情况和空间坐标的情况下，求解机械手各指节的转角θi，以此来验证机械手运动学问题，实现机械手的运动参数从操作空间到关节空间的映射。

由式(7)和式(8)求得

(10)

由式(7)和式(9)求得

(11)

化简后得

As2+Bc2=C

(12)

所以，可得

(13)

同理，由式(9)得

Ds3+Ec3=F

(14)

其中，D=l3c2；E=l3s2；F=z-l2s2。

同上可得

(15)

至此，机械手的3个指节转动角度均已求解出来，逆运动学的分析计算对控制机械手达到期望的位姿提供了理论依据。同时，也从侧面证明了机械手正运动学计算过程的正确性。

3 运动仿真

对欠驱动仿生机械手完成整体设计和正逆运动学理论计算后，利用MATLAB软件中的Robotics Toolbox工具箱，对机械手进行仿真模型的建立并验证其抓取运动空间以及相关运动参数，通过相关参数的可视化图形验证机械手设计的可行性。

由于机械手采用模块化设计，每根手指的运动控制情况相同，现对其中任意1根手指进行进行分析，基于前面所建立的D-H模型，使用Robotics Toolbox使用Link()函数建立其对应的连杆模型，如图5所示。并依据各指节的变量关系及变化范围，利用蒙特卡洛算法求解机械手单根手指的抓取运动空间，运用fkine()函数生成空间点集云图[13-14]， 如图6所示。由于各手指根部的基座与平台固定，故单根手指的运动空间点集云图为二维平面图，并在XOZ平面内的空间投影图，如图7所示。根据手指模型在空间内的点集云图对应的坐标参数，与运动学理论计算结果一一对应，验证了前面运动学分析的合理性。

图5 机械手指连杆模型

图6 机械手指运动空间

图7 机械手指运动空间XOZ平面投影

完成机械手空间运动仿真验证后，采用jtraj()函数对机械手各指节在抓取运动过程中的角度、角速度和角加速度的变化过程进行插值计算。仿真结果如图8～图10所示。由仿真结果曲线可知，机械手在完成抓取动作的过程中，动作连续，运行平稳。3个指节的角度变化持续稳定，各指节的角速度、角加速度的始末值为0，运动变化曲线连续且光滑，未出现突变等情况。说明该机械手在完成抓取运动的过程中运行稳定，受到振动变化影响小，能够稳定可靠的完成抓取任务。

图8 各指节角度变化曲线

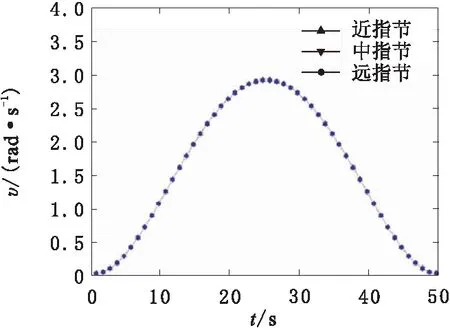
图9 各指节角速度变化曲线

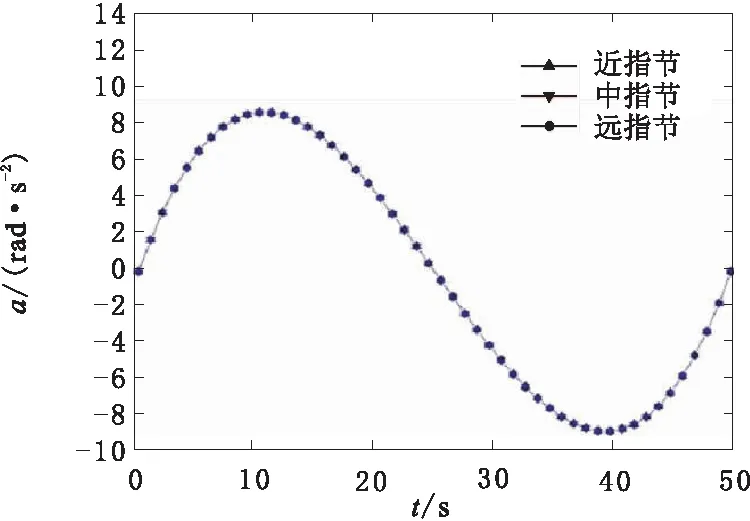
图10 各指节角加速度变化曲线

4 结束语

本文针对坛装酒生产企业过度依靠人工完成工作的问题，提出了一种配合机械臂使用的九自由度仿生型欠驱动机械手。其设计合理，能够满足任务抓取要求，为后续实验样机的制作提供了有效的理论依据。