基于蒙特卡罗方法的IVR熔融池内热源时序模型构建及分析

陈俊逸，黄善仿，郝以昇，刘国栋，胡钰文，黎 阳,*，宫厚军，昝元锋，郭啸宇，骆 浩

(1.清华大学 工程物理系，北京 100084；2.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室，四川 成都 610041)

堆内熔融物滞留(IVR)作为反应堆严重事故的关键缓解策略，其具体内容为：严重事故发生时，堆芯熔融物向压力容器下封头内迁移形成熔融池。熔融池内残余核燃料及裂变产物释热对壁面持续加热。冷却水完全淹没下封头外表面，通过气液两相自然循环保证充分带走压力容器外表面热量。

IVR由加州大学圣塔芭芭拉分校(UCSB)的Theofanous教授提出，并基于其自主开发的面向事故的风险分析方法(ROAAM)对反应堆严重事故下形成的熔融池进行了分析。结果表明，壁面热流密度是否超过临界热流密度(CHF)，是评价IVR结构性能的关键指标[1]。

数年来国内外开展了大量试验，以基于CHF探索严重事故下IVR的安全特性。Theofanous教授开展了COPO及ACOPO实验[2]，对下封头二维熔融池模型进行了传热分析，并得到了用于预测下封头CHF随角度变化的表达式。Sehgal教授开展了SEMICO实验[3]，对池内雷诺数及壁面热流密度进行了探索。西安交通大学基于不同熔融池结构开展了COPRA实验[4-5]，针对熔融池内对流进行CFD模拟，探索了速度场与温度场的分布。俄罗斯Korchatov研究所于RASPLAV与MASCA实验中发现了重金属层分布于底部的熔融池三层构型[6]，进而分析了IVR的安全性。

上述实验与模拟，均为人工设置恒定热源模拟体积热源，不能精确反映熔融池释热随时间与空间的变化，增加了热流密度测量及模拟的不确定性。为精准模拟熔融池内衰变热，清华大学基于反应堆蒙特卡罗(RMC)程序及内耦合燃耗/衰变热计算程序DEPTH提出了面向熔融池内物理过程的新衰变热计算方法，并验证了其可行性与准确性[7]。然而，堆芯运行不同时刻的核素组分不同，熔融池释热规律及物理过程不尽相同。前述研究未能进一步探索堆芯运行不同时间形成熔融池的释热特点及物理规律，因此需要建立熔融池内热源时序模型，并分析相应的物理机理。

本文基于RMC程序和BEAVRS基准题，通过RMC程序的构建实体几何(CSG)方法对熔融池结构进行精细化建模与燃耗区划分。通过蒙特卡罗方法模拟熔融池内中子输运及相关核反应，使用线性子链方法求解燃耗方程进行IVR熔融池内燃耗计算及裂变产物衰变链模拟，分析熔融池内物理过程，以建立精准的熔融池内热源时序模型，并从物理分析角度对变化趋势进行评价，为IVR策略安全及设计提供参照。

1 计算方法

1.1 反应堆蒙特卡罗程序

RMC程序是清华大学工程物理系REAL实验室自主研发的蒙特卡罗中子输运程序，兼具临界计算、燃耗计算、中子/光子/电子耦合计算、全堆换料计算、衰变热计算等功能，具有良好的并行计算效率。通过面向BEAVRS等基准题的验证计算，证明RMC程序具有较高的准确性[8]。

DEPTH模块为RMC程序内置燃耗计算模块，实现了内耦合的燃耗计算及衰变热计算等功能，具备大规模的燃耗计算能力，可用于计算压水堆全堆燃耗[9-10]及模拟熔融池中核素组分变化。燃耗计算与衰变热计算的准确性已在文献[7,10]中得到了验证。

1.2 计算流程

针对RMC程序及DEPTH程序，本研究结合全堆计算与燃耗/衰变热计算两个模块，进行迭代求解，计算流程图如图1所示。具体计算步骤如下：1)BEAVRS堆芯建模及全堆输运计算，在指定燃耗步输出堆芯中核素的绝对原子密度；2)基于BEAVRS基准题对堆芯组分质量进行计算，得到三层熔融池各层体积，构建熔融池模型；3)细网格划分熔融池燃耗区，熔融池燃耗计算得到各燃耗区的中子通量及核反应功率，更新熔融池材料；4)对熔融池进行衰变热计算[7]，输出燃耗区内释热功率，更新材料并进入下一个全堆燃耗步长；5)循环运行步骤1～4，直到全堆计算进入最终燃耗步，结束计算。

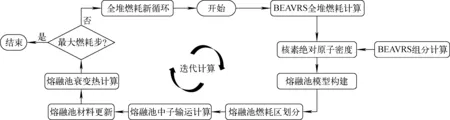
图1 熔融池分时刻释热功率计算流程图

1.3 衰变热计算

熔融池释热过程中，不能忽视衰变热的贡献。RMC程序结合了衰变热计算与燃耗计算以描述核素的变化规律。燃耗计算的核心是求解经典点燃耗方程，描述核反应系统中核素随时间的变化规律。燃耗链中核素与时间相关的点燃耗方程如下：

(1)

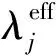
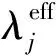
(2)

(3)

式中：λi为第i个核素的衰变常量；φ为中子通量；σi,j为第i个核素反应生成第j个核素的反应截面。

常用的燃耗方程求解方法主要有两类，分别为线性子链法与矩阵指数法。本文采用线性子链法(TTA)将复杂的燃耗链分解为独立的线性燃耗子链，然后对每条线性子链解析求解。

对1条线性子链，假设顶端核素初始核密度为n1(0)，则线性子链第k个核素经时间t后的核素密度nk(t)为：

(4)

(5)

(6)

针对反应堆停堆以及熔融池等场景中常见的衰变热计算需求，DEPTH模块内置了衰变热计算功能[5]。基于中子注量与绝对原子密度直接计算燃耗区内的衰变热释热功率Q，即：

Q=Rq=Nλq

(7)

式中：R为核反应率；q为核素每次衰变放出的热量。

2 计算模型构建

2.1 BEAVRS全堆模型构建

RMC程序具有几何模型构建功能，能基于层级空间的几何描述系统以及CSG方法进行三维模型的构建。

基于层级空间的几何描述系统通过空间结构的层级嵌套，不仅能分层表示反应堆各结构，如燃料棒、导向管、仪表管、燃料组件、全堆堆芯等，还可用于下封头熔融池的建模。RMC程序构建的BEAVRS全堆几何模型示意图如图2[8]所示。全堆计算设置为：每轮迭代采用100万粒子数，100个非活跃代和500个活跃代，收敛误差为0.000 01，进行全堆燃耗计算，获取各燃耗步的核素信息作为熔融池建模边界条件。

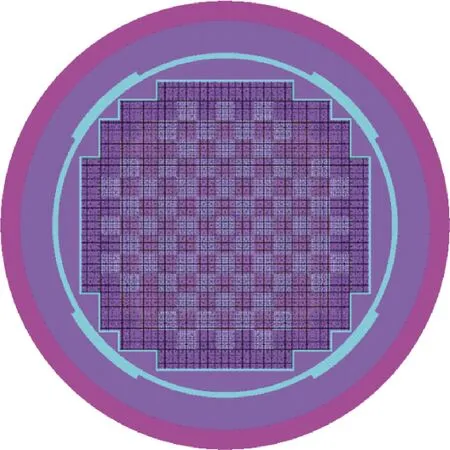
图2 BEAVRS全堆几何模型示意图[8]

2.2 熔融池模型构建

国内外对熔融池几何结构的建模已有较多研究，对于三层熔融池，较有代表性的有Esmaili等[11]基于MASCA理论的三层模型、Seiler等[12]的保守三层模型以及Salay等[13]的基于熔融池热化学性质的三层模型，后者已应用于MAAP5。

本文基于全堆熔化工况，作出下述假设以进行熔融池各层参数计算：1)轻金属层的成分为金属Zr以及不锈钢(SS)；2)氧化物层的主要成分为UO2及ZrO2，设置金属Zr的氧化率为0.5；3)重金属层的主要成分为金属U和金属Zr；4)裂变产物基于全堆燃耗计算结果，均匀分布在氧化物层与重金属层中。

计算得到了三层熔融池结构各层建模参数。本工作建模方法与文献模型参数计算结果列于表1。

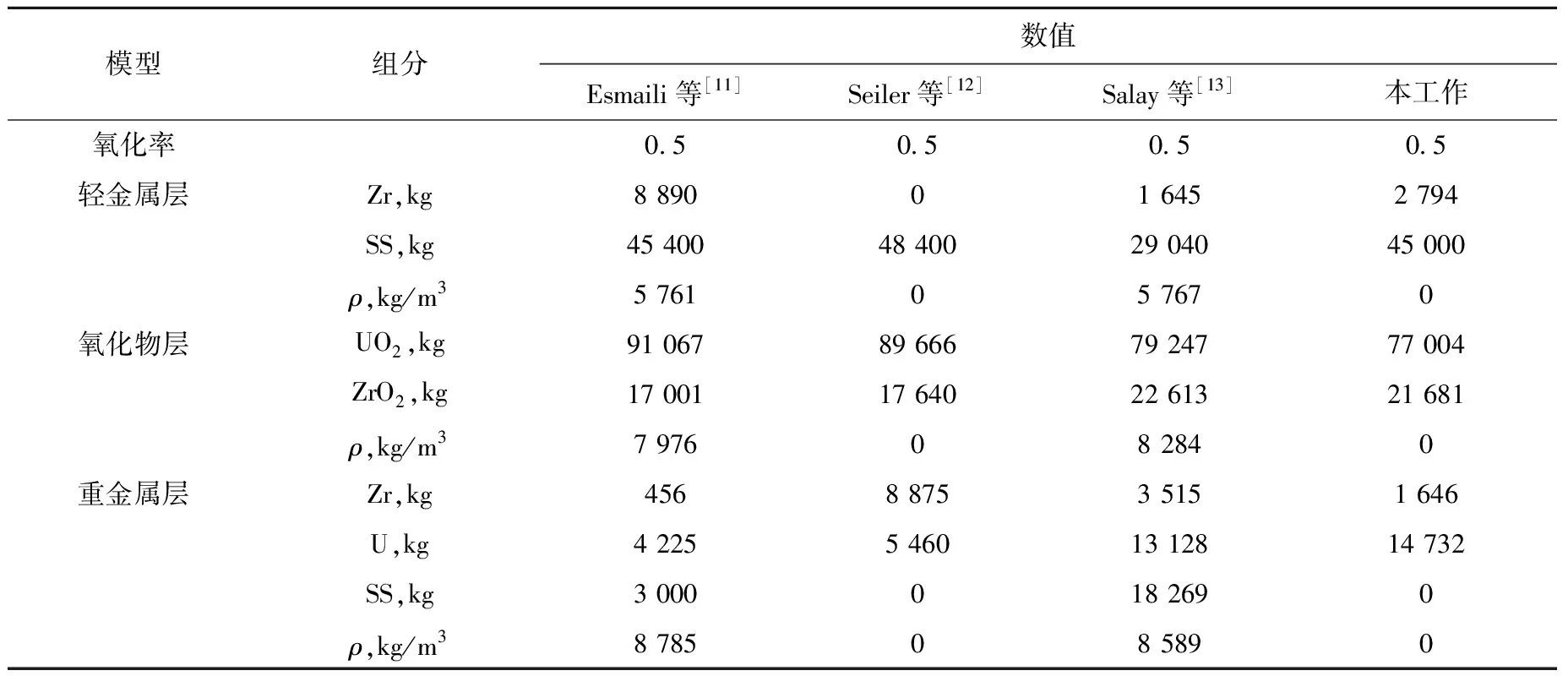
表1 本工作与文献建模参数计算结果

2.3 熔融池燃耗区划分

熔融池形成后，池内可能存在活化裂变产物等核素放出中子并引发次级核反应，对熔融池中不同区域的材料密度造成影响，进而影响释热功率。需要对熔融池进行细网格区域划分，从而获得更准确的释热功率分布。

本文将下封头熔融池沿z轴(高度)方向进行分层，其中，裂变产物主要聚集于氧化物层。将轻金属层分为5层、氧化物层分为12层、重金属层分为4层。每层沿半径方向分为11层，沿圆周方向分为18层。轻金属层分989个燃耗区域，氧化物层分2 015个燃耗区域，重金属层分287个燃耗区域，共3 291个燃耗区实现对下封头熔融池三层结构的完全分区和填充[5]。

严重事故下，压力容器被两相流体淹没并发生沸腾换热。为探索两相流边界条件中产生的气泡可能对中子输运造成的影响，本文采用弦长抽样方法，将气泡视为外部冷却水基体中的弥散介质，对下封头外侧两相流体边界条件进行建模[14]。三层熔融池的下封头及外部气液两相流模型如图3所示。

图3 熔融池燃耗区划分策略

3 计算结果与分析

3.1 反应堆运行时刻选取

反应堆运行期间，中子变化复杂，核素分布多样，因而在运行任一时刻发生严重事故，形成的熔融池皆具有不同的释热特性。本文选取BEAVRS百万千瓦级压水堆满功率运行中的数个时间点作为严重事故熔融池示例，分别为装料后运行5、30、40、70、150、200、250、300 d。通过DEPTH程序进行BEAVRS全堆燃耗计算。基于相应运行时刻的核素信息，选取重要核素作为熔融池初态核素组成边界条件，计算熔融池释热功率[15]。

3.2 熔融池时序模型构建及分析

对熔融池体积热源的模拟，一方面要考虑由于核素衰变释放的衰变热，另一方面要考虑熔融池中裂变碎片及自发裂变核素等释放中子、残余核燃料裂变等的核反应释热。

通过RMC程序在熔融池内初始化点中子源，能有效模拟熔融池中的中子输运。RMC程序设置每轮迭代采用10万粒子数，20个非活跃代和100个活跃代，收敛误差为0.000 2，时间步长为0.05 d。

反应堆运行5 d和40 d后熔融池释热功率变化规律示于图4。由图4a可看出，运行5 d后，熔融池释热功率呈指数形式衰减，变化趋势与文献[7]计算结果相符。释热功率最大值出现在最初燃耗步，为2.5 MW，然后迅速下降，在第3燃耗步处下降到约50 kW且逐渐趋于平缓(图4b)，于第5 d衰变热功率降于初始的0.05%，可忽略。这体现了熔融池形成初期，熔融池内中子对熔融池释热功率存在影响。释热功率较低是由于可裂变核素尚未大量裂变并产生裂变产物，抑制了衰变热的产生。熔融池迁移初期的峰值对IVR包容失效的威胁需要得到关注。

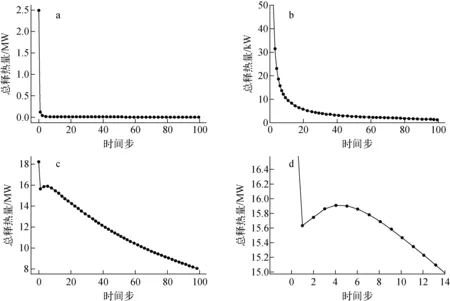
图4 熔融池释热功率变化规律

堆芯运行40 d后，熔融池5 d内以及1～2 d内的衰变热总功率变化趋势与曲线极值处的变化规律分别示于图4c、d。由图4d可看出，最大释热功率出现在约18 MW处，随后在第2燃耗步陡降于16 MW以下，又于第3燃耗步重新上升，在第0.2 d达到极值，再以指数衰减形式持续下降。极值的产生使释热衰减趋势减缓，这反映熔融池中裂变产物的衰变释热主导了释热功率变化。

堆芯运行30、70、130、200、250、300 d的熔融池释热功率与时间关系曲线示于图5。该模型燃耗步设置为30步，前10步时间步长为0.1 d，后20步时间步长为0.2 d，模拟了5 d内的衰变热功率变化情况。图5显示，随着运行时间的增加，熔融池释热功率增加。装料初期由于核燃料未完全消耗，导致所形成熔融池中裂变产物较少，衰变热释热功率较低。另一方面，运行250 d与运行300 d的熔融池释热功率曲线完全重合，说明熔融池内核素组分在运行250 d后已趋于稳定，计算最大释热功率为22 MW。

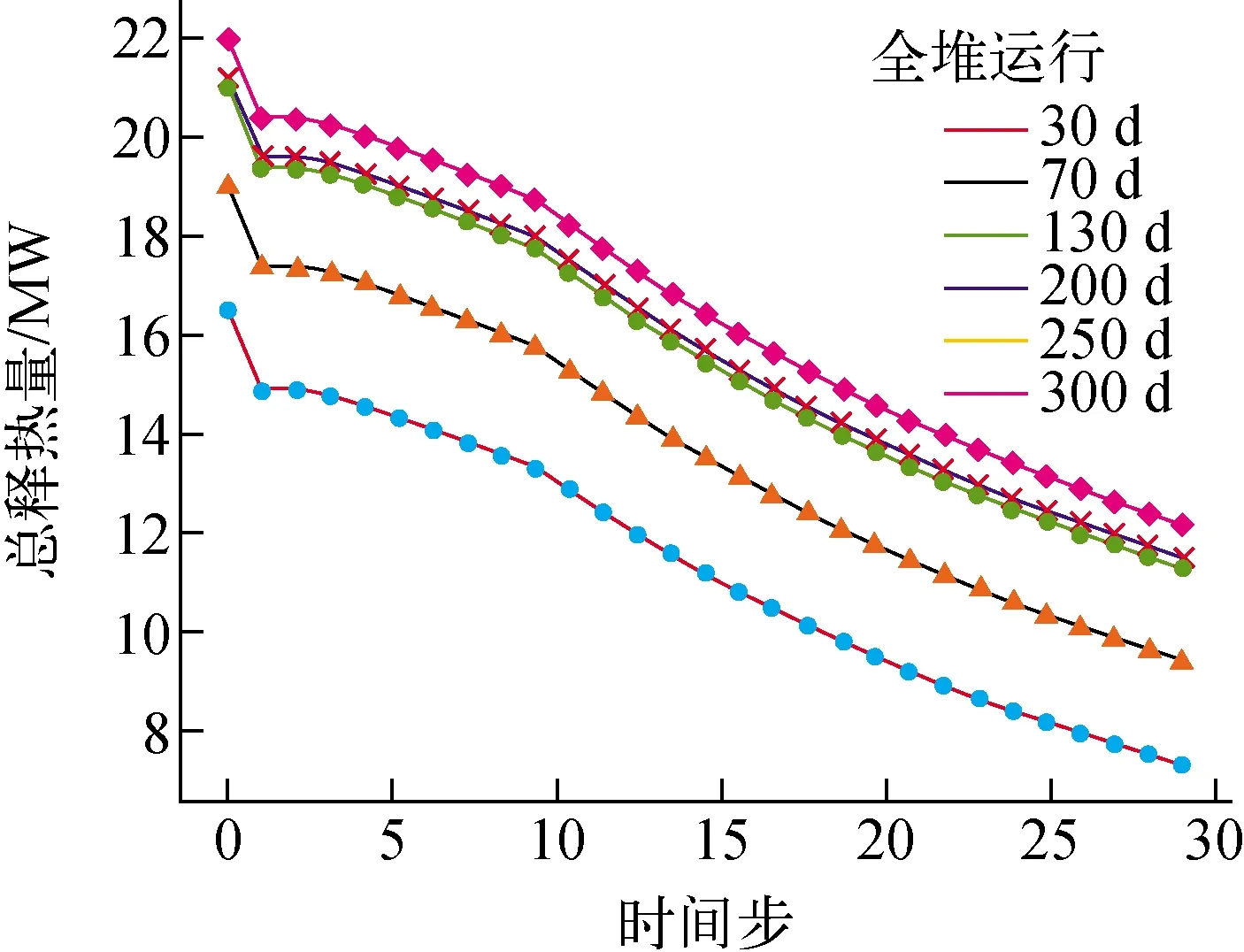
图5 运行不同时间熔融池释热功率变化曲线

运行300 d后熔融池截面内部栅元释热功率密度分布随时间的变化示于图6。图6显示，熔融池形成初期(0.1 d)由于熔融池内中子的影响，中心部分释热功率相对较高，有较大的功率密度；于0.3 d时各栅元功率密度尚有微弱差异，随后趋于均匀并稳定下降。这反映出随着裂变产物的逐渐衰变，燃料裂变的释热影响可被忽略，释热逐渐被裂变产物衰变释热主导。轻金属层中因存在部分轻裂变产物有少量衰变释热，功率密度相对于氧化物层与轻金属层可忽略。

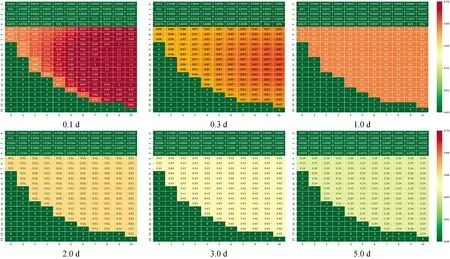
图6 运行300 d后熔融池释热功率密度变化规律

4 结论

本研究采用反应堆蒙特卡罗软件RMC及燃耗/衰变热计算模块DEPTH，对严重事故下熔融池内热源的变化规律进行了计算，并基于得到的数据进行曲线拟合，得到了时序模型。通过研究，得到如下结论。

1)考虑熔融池内由于活化裂变碎片、自发裂变核素等释放出中子，初期热源分布呈中心高于四周的特性，体现了熔融池内的中子输运影响熔融池核素组成，并主导熔融池形成初期的释热变化。

2)反应堆运行不同时刻形成的熔融池，释热功率变化为相似的指数衰减趋势，其值则随堆芯中裂变反应程度不同而发生改变。全堆运行250 d时，熔融池材料组成达到稳定，最大释热功率达22 MW，裂变产物衰变主导了熔融池形成后期的释热变化。

3)以往的研究认为，熔融池内热源仅存在于下封头氧化物层中，而反应堆运行期间可能产生轻核素，如Zr的同位素存在于轻金属层且放出衰变热。轻金属层作为热源对熔融池传热、聚集效应、下封头壁面蠕变等产生的影响需进一步验证。

本研究结果及时序模型可用于更精确地反映堆严重事故诊断及IVR性能模拟，为IVR的性能测试及设计提供数据支撑。