丝网芯内钠薄液膜蒸发与毛细特性研究

马誉高，张英楠，余红星，黄善仿,*

(1.清华大学 工程物理系，北京 100084；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

碱金属热管是一种利用毛细力驱动的高效非能动传热元件，主要应用于核能、航空航天等领域[1-4]。由于特种用途对于几何尺寸和重量的严格限制，碱金属热管管径通常较小(小于20 mm)，在该尺寸下一般采用金属丝网芯结构。丝网芯提供的毛细力是热管内工质自然循环的最终动力来源。

毛细力由丝网内的液膜形态决定，而液膜形态受丝网几何构型及工质与丝网的润湿特性影响。其中，丝网芯的几何构型由丝径、孔径等参数决定，工质与丝网的润湿特性受丝网与工质间分子作用力、界面形态、粗糙度和运行温度等因素影响。

在理论方面，已有大量学者针对毛细孔内蒸发薄液膜的传热传质过程开展了研究，其难点在于液膜与固体接触线的微观形态描述。当前的主流理论认为，在宏观的三相接触点处吸附有纳米级厚度的前驱膜。前驱膜理论解决了三相点直接相交带来的应力奇异性问题(Huh-Scriven佯谬[5])，该理论已在实验上得到了证实[6-11]。1976年，Wayner等[12]基于前驱膜理论，提出了相变传热中接触线上的吸附和毛细管冷凝模型，并系统性地建立了一维液膜传热传质本构方程。Wayner将液膜分为3个区域，包括平衡液膜区、蒸发薄液膜区和本征液膜区。在平衡液膜区，存在纳米级厚度的静止液膜；在蒸发薄液膜区，液膜开始流动导热，并在气液界面发生相变，液膜厚度上升，液膜受分离压力和毛细力的共同作用；在本征液膜区，液膜的曲率趋于定值，液膜主要受毛细力的作用。Wang等[13-14]、寇志海[15]、金鑫[16]以及Hanchak等[17]基于Wayner模型进行了进一步研究，针对非极性工质，发展了一维毛细孔蒸发弯月面液膜理论，对氨、甲醇、戊烷和正辛烷等非极性工质进行了分析，考虑过热度、孔径、蒸发冷凝系数和固液界面滑移等因素对液膜的传热传质和润湿特性的影响，对初始液膜厚度进行了敏感性研究。在这一阶段的研究中，由于非极性工质热导率低(一般低于丝网芯材料2个数量级)，传热过程通常简化为一维导热模型。Tipton等[18-19]在Wayner理论的基础上，进一步考虑了分离压力的电子分量(电场力)，对圆柱孔内的钠液膜进行了计算。分析表明，在液态金属薄膜的传热传质与润湿过程中，电场力的作用不可忽略。

为进一步研究碱金属工质在丝网芯中的毛细和浸润特性，本文以前驱膜理论和蒸发液膜理论为基础，考虑钠工质的高导热率特性与丝网芯的圆柱几何结构，基于广义Young-Laplace方程、Hertz-Knudsen-Schrage方程、Kelvin方程和稳态导热方程，建立液态钠在丝网芯内的蒸发薄液膜传热传质与铺展模型，对液态钠工质在丝网芯表面的浸润现象和毛细现象进行分析，并探究不同运行参数对钠液膜传热传质与毛细特性的影响。

1 模型与方法

本文基于前驱膜理论和蒸发液膜理论建立微观液膜模型。计算模型包括广义Young-Laplace方程、Hertz-Knudsen-Schrage方程、Kelvin方程和稳态传热方程。

在对纯液态金属工质分析中，考虑其分子特性对分离压力的影响，以及高热导率对液膜和壁面横向传热的影响。同时考虑丝网芯几何形状对液膜分布的影响，在一维平板模型的基础上建立一维圆柱模型。使用Bond数(Bo)衡量重力与表面张力的相对效应：

Bo=ρgL2/σ

(1)

其中：ρ为液相密度；g为重力加速度；L为特征尺寸，取丝网孔径；σ为表面张力。

当丝网孔径达到100 μm以下时，Bo降低至10-3量级，此时表面张力σ远大于重力，因此忽略丝网内液膜所受重力。本文采用的基本假设为：1)工质和壁面热物性参数为常数；2)气相工质为饱和蒸汽；3)液相工质的流动状态为不随时间变化、不可压缩层流流动；4)忽略热毛细力对传热传质的影响以及马兰戈尼对流效应。

1.1 压力控制方程

毛细蒸发薄液膜模型需要首先建立气液界面两侧的压强关系。Young和Laplace在1805年提出了Young-Laplace方程，认为气液界面两侧的压强差为毛细压强[5]。随着研究的深入，广义Young-Laplace方程考虑了分离压强，认为气液界面两侧的压强差是由毛细压强pc和分离压强pd共同决定的：

pv-pl=pc+pd=pc+pd,vdw-pd,ele

(2)

式中：pv为气相压强；pl为液相压强；pd,vdw为范德华分量；pd,ele为电子分量。式(2)表明，在常物性的假设下，毛细压强pc和分离压强pd只与液膜厚度的0～2阶导数有关。对于液态钠工质，毛细压强pc与气液界面的曲率有关；分离压强pd与液膜的厚度有关，包括范德华分量pd,vdw和电子分量pd,ele。

对于任意的气液界面，毛细压强pc的表达式为：

pc=σ(K1+K2)

(3)

其中，K1和K2为曲面上任意两个互相垂直平面的曲率，两个曲率之和为定值[20]。在不同的曲面和维度下，曲率的取值也不完全相同。如在毛细管中，毛细管半径为r，若假设曲面为球面，则K1=K2=cosθ0/r；若曲面不为球面，则K1=δ′/(1+δ2)1.5、K2=δ/(r-δ)(1+δ2)0.5，其中δ1为液膜厚度。在一维模型下，K1=K=δ′/(1+δ2)1.5、K2=0。

在一维模型下，分离压强的范德华分量和电子分量具体表达式为：

(4)

1.2 蒸发质量通量

在液膜中所传导的热量，除少部分用于提供工质在流动中升温所需的焓变，绝大部分用于工质在气液界面发生蒸发相变。计算气液界面上净蒸发质量通量最常用的方程为Hertz-Knudsen-Schrage方程[15]：

(5)

其中：m″为蒸发质量通量；α为蒸发冷凝概率；M为液相原子质量；Rg为气体常数；p为压强；T为温度，下标v表示气体，lv表示气液交界面；pv_equ为气液界面平衡蒸汽压；psat为气相饱和压强。

若气液界面存在曲率，且满足薄液膜的假设，则毛细压强和分离压强对气液界面平衡蒸汽压的影响不可忽略。基于Kelvin方程对气液界面平衡蒸汽压进行修正[5]：

(6)

其中气相饱和压强可通过相应的热物性方程进行计算。可见，当毛细压强与分离压强之和越大，越倾向于使液膜脱离壁面时，对工质蒸发的抑制程度越强；反之，则促进工质的蒸发。若已知参考温度和相应的参考饱和压，当气液界面温度与参考温度差异较小时，也可通过Clausius-Clapeyron方程[5]计算：

pv_equ(Tlv)=psat_ref(Tsat_ref)·

(7)

蒸发质量通量不仅与毛细压强和分离压强有关，同时也与液相压强的1阶导数有关。基于不可压缩层流流动的假设，同时假设固液界面无滑移、气液界面无剪切力，液相压强与蒸发质量通量可通过如下表达式计算：

(8)

其中：ν为液体黏度；θ为接触角。

对式(8)求导，可得到：

(9)

基于上述分析，式(2)～(9)在液相压强、毛细压强和分离压强与蒸发质量通量之间建立了联系，从而实现液膜润湿特性与传热传质的耦合计算。

1.3 传热模型

在对水和有机物等非极性工质进行薄液膜分析计算时，往往将壁面边界假设为定壁温边界条件，不考虑横向传热[14]。这是因为与金属材质的壁面相比，水和有机物等非极性工质的热导率非常小，热量几乎全部通过壁面传导，壁面温度的变化在计算中可忽略，因此定壁温的假设合理。但对于液态碱金属工质，液膜热导率与壁面热导率相当，甚至高于壁面热导率。在这一工况下，液膜和壁面的横向传热不能忽略，温度梯度的主方向为计算方向，定壁温边界条件也不再适用，需要建立新的传热方程。

忽略厚度方向上的温度梯度，则在xi处，壁面和液膜的温度均为定值，即：

(10)

本文模型中，不同的传热路径对应不同的热阻，从而建立工质液膜的热传导模型。

1.4 接触角

在丝网芯热管中，影响丝网芯抽吸能力的一个重要指标是接触角。确定不同工况下接触角的大小、分析接触角的影响因素，是微观液膜模型实现的主要任务之一。赵亚博[5]提出了两种计算接触角θ0的方法，第1种为微观方法，设分离压强pd的不定积分为Π，即Π′=pd，通过修正的Frumkin-Derjaguin方程计算接触角：

(11)

第2种为宏观方法，即选取蒸发液膜区和本征弯月面交界处位置的斜率作为接触角。

这两种方法均存在一定缺陷，微观方法的缺陷在于难以确定合适的平衡液膜厚度以及在平衡液膜厚度下液膜所受到的力的种类和具体表达式；而在宏观方法中，对于判别液膜进入本征弯月面的标准尚未统一，通过主观判断会引入较大的不确定性。

因此，本文提出了第3种计算接触角的方法，即假设在距离平衡液膜区足够远的位置，气液界面曲率为定值，沿圆弧对气液界面进行延伸，直至与壁面相交，认为气液界面与壁面在这一点的夹角为接触角。若二者相切或相离，则认为接触角为0。

2 模型验证

本文对微观液膜模型进行校核。Hanchak等[17]使用显微反射法测量了正辛烷蒸发薄液膜在毛细孔内的液膜厚度变化，测量精度为±1 nm。实验中，正辛烷为非极性有机工质，因此分离压力只需考虑范德华分量；其热导率较小，不考虑横向传热，采用定壁温模型。正辛烷工质的物性参数列于表1，通过式(7)计算气液界面温度的饱和压强。

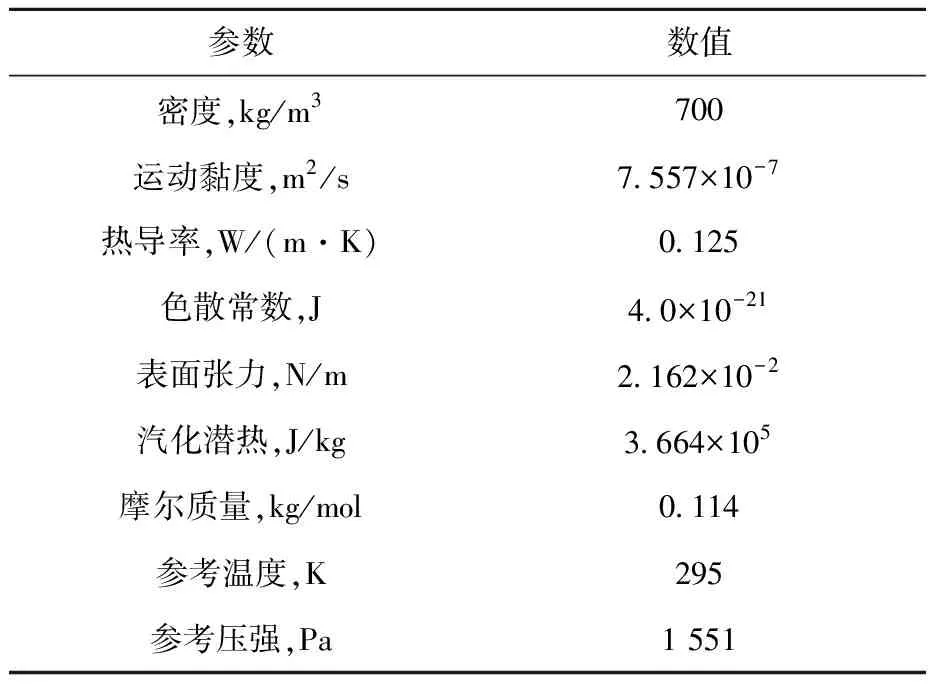
表1 正辛烷工质物性参数

利用微观液膜模型计算不同工况时所使用的运行参数列于表2，其中蒸发冷凝系数、运行温度和过热度均与Hanchak等[15]的结果保持一致。不同工况下微观液膜模型计算结果与实验案例的液膜厚度分布示于图1，实验误差棒高度为±10 nm。在微观液膜模型中，固定初始液膜厚度为20 nm，通过调节初始液膜厚度2阶导数，得到不同的液膜厚度分布。Hanchak等也对实验结果进行了数值模拟，其模拟结果与实验比对的最大误差为35 nm，平均误差在10 nm以内。本文所构建的微观液膜模型最大误差为35 nm，平均误差在10 nm左右，基本达到相同水平，验证了本文模型的稳定性与准确性。

图1 正辛烷工质微观液膜模型与实验案例液膜厚度分布对比

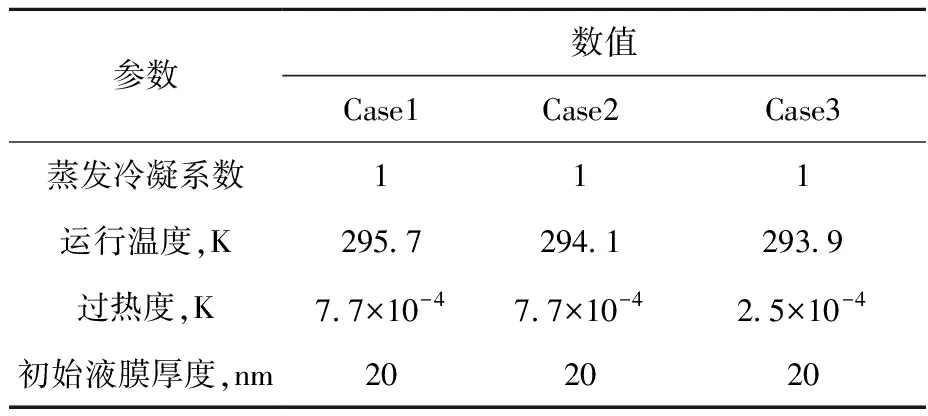
表2 正辛烷工质运行参数

在模型层面，液态钠和正辛烷的差异性主要体现在工质热物性和分子作用力种类上，但控制方程的形式并未改变。

3 蒸发薄液膜参数敏感性分析

本文将对影响液态钠薄膜的传热传质与润湿特性的运行参数进行逐个分析，包括运行温度、过热度、蒸发冷凝系数、丝网芯尺寸和液膜位置。其中过热度的定义为三相接触线处液膜温度和运行温度(即气相温度)的差值。本文的敏感性分析将基于基准运行参数(表3)展开。

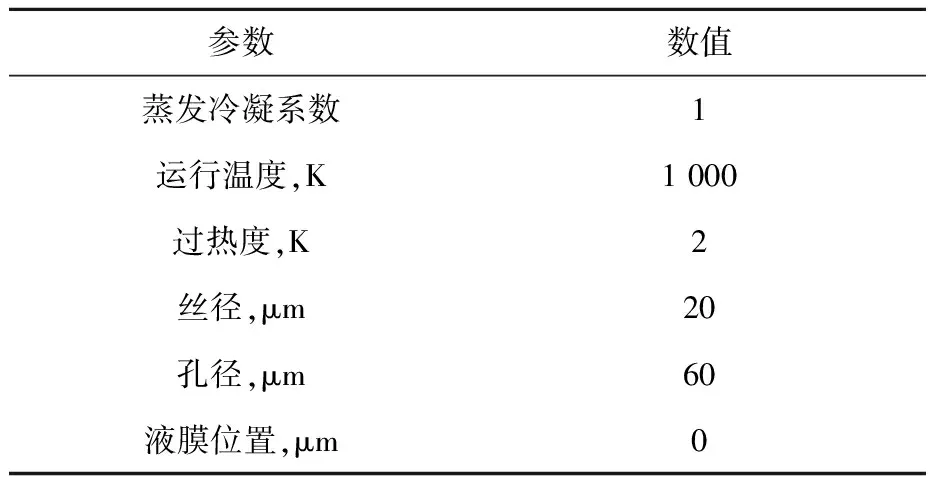
表3 基准运行参数

3.1 运行温度、过热度和蒸发冷凝系数的影响规律

首先在一维平板模型下，对运行温度、过热度和蒸发冷凝系数进行分析。在其他学者[13-17]的研究中，这3个参数已被广泛分析，结论也较统一，且普遍适用于目前已知工质。在不同运行温度、过热度和蒸发冷凝系数的工况下，计算得到的热流总量列于表4，液膜厚度和蒸发质量通量分布示于图2。可见，在不同运行温度、过热度和蒸发冷凝系数下，液膜厚度分布趋势基本一致；蒸发质量通量分布趋势相似，但数值相差较大。计算的运行温度区间为800～1 200 K，接触角从7.5°上升至9.5°，热流总量从10 W/m上升至2 090 W/m；过热度区间为0.1～10 K，接触角从7.5°上升至9.0°，热流总量从7.5 W/m上升至805 W/m；蒸发冷凝系数区间为0.001～1，接触角从7.5°上升至8.0°，热流总量从0.05 W/m上升至155 W/m。

表4 不同运行温度、过热度、蒸发冷凝系数工况下的热流总量

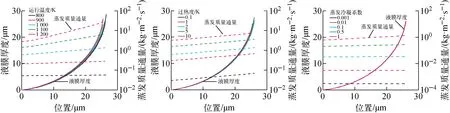
图2 运行温度、过热度和蒸发冷凝系数对液膜厚度和蒸发质量通量分布的影响

综上，运行温度、过热度和蒸发冷凝系数对接触角基本无影响，对热流总量有量级上的影响，即运行温度越高，热流总量越高；过热度越大，热流总量越高；蒸发冷凝系数越大，热流总量越高。这一结论也可从液态钠工质的热物性[23]及式(6)中得到体现。

3.2 丝径、孔径和液膜位置的影响规律

对上述一维平板模型参数分析的结论同样适用于一维圆柱模型。在一维圆柱模型中，除丝径和孔径外，液膜位置(即三相接触点在弧上的位置，液膜位置减小代表液膜后退)也会对计算结果产生影响，这在一维平板模型中无法考虑。如在一维平板模型下，曲率半径R和孔径Rc、接触角θ0的关系为：

R=Rc/cosθ0

(12)

而在一维圆柱模型下，还要考虑水平倾角φ和丝径Rw，如图3a所示。

(13)

可见，曲率半径很大程度上取决于液膜位置。对于简单方形毛细孔模型，其俯视图是密接正方形。假设三相接触线的高度相同，且曲率半径R1=R2=R，则单孔毛细力F的表达式为：

(14)

液膜在丝网内后退的过程如图3b所示。可见，在液膜后退的过程中，气液界面在计算方向上的投影面积先下降后上升，曲率半径变化趋势与具体的接触角和水平倾角有关。当水平倾角大于90°时，液相工质力学平衡稳定性差，液膜难以在这一几何下维持稳定。400目不锈钢丝网下单孔毛细力随接触角和竖直角(竖直角为水平倾角与接触角之和，反映三相接触点在圆柱截面上的位置)的变化示于图4，运行参数与基准工况参数相同。图4中，实线位置的水平倾角小于90°，液膜稳定性较好，接触角越大，毛细力越大；虚线位置的水平倾角大于90°，液膜稳定性较差，接触角越大，毛细力越小。可见，在不同的接触角下，随着竖直角的增加，毛细力均出现先上升后下降的变化趋势，且接触角越大，极值点出现的竖直角越大，数值也越大。如果只考虑水平倾角小于90°的工况，则当接触角相同时，毛细力随着竖直角单调上升。从前文分析可知：在运行温度较高的工况下，液态钠工质的润湿性较好，接触角较小，因此毛细力随液膜接触线位置的变化存在拐点。因此在一定范围内，液膜在丝网内回退将提升毛细力，但当液膜进一步在丝网芯内部回退时，便有可能发生液膜接触线位置下降同时毛细力下降的正反馈现象，导致局部干涸。

图3 一维圆柱模型(a)和液膜后退过程(b)示意图

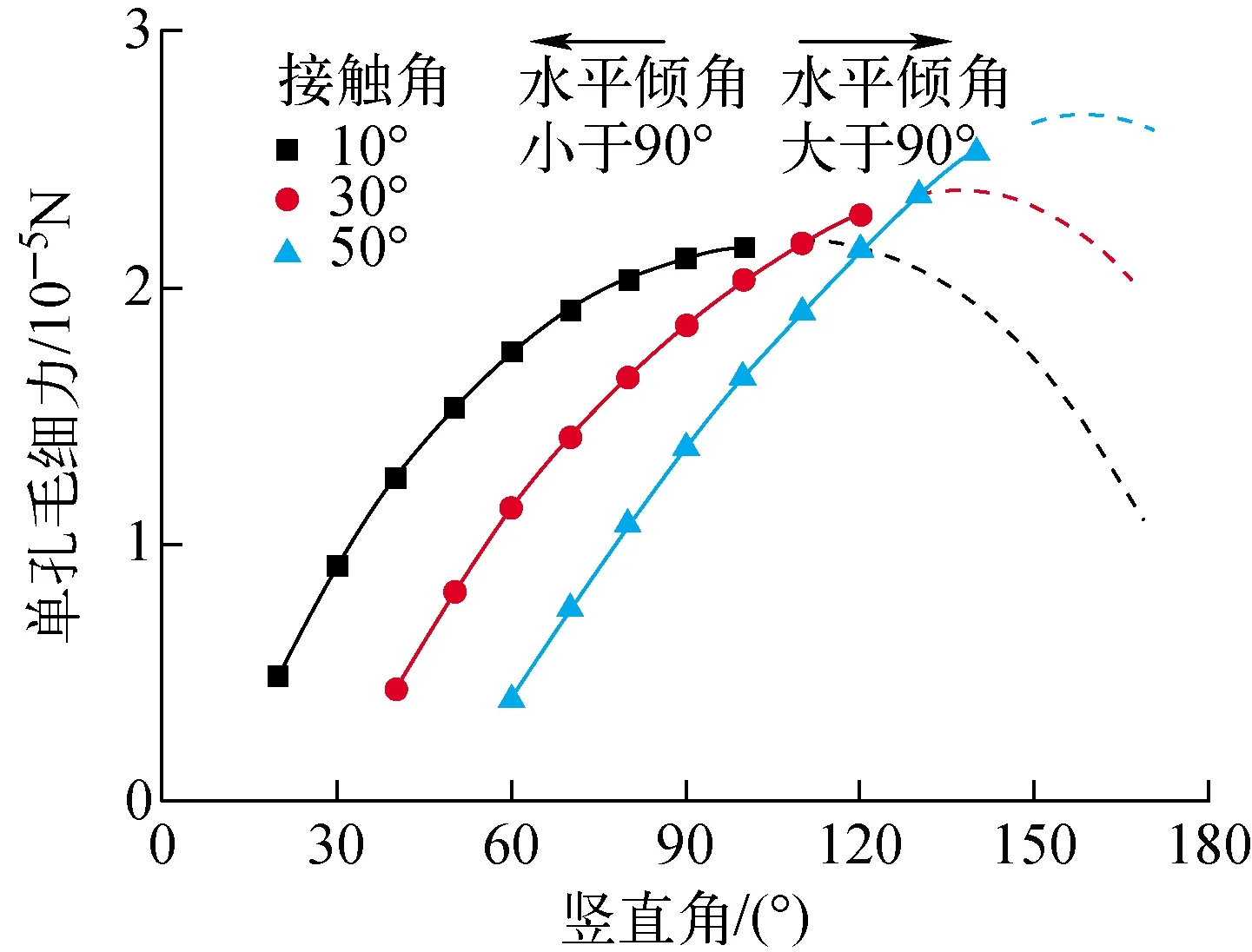
图4 单孔毛细力分布

不同丝径、孔径和液膜位置下计算得到的热流总量列于表5。可见，这些参数对液膜厚度分布和蒸发质量通量分布产生了影响。丝径区间为10～50 μm，热流总量从120 W/m下降至15 W/m；孔径区间为40～80 μm，热流总量从35 W/m上升至175 W/m；液膜位置区间为3～-1 μm，热流总量从65 W/m上升至225 W/m。

表5 丝网芯尺寸工况

对于不同的丝径和孔径，从孔隙率角度考虑，孔隙率越大，气液界面的面积越大，从而影响蒸发质量通量分布和热流总量。因此，丝径越大，热流总量越低；孔径越大，热流总量越高；液膜越后退，热流总量越高。不同丝径、孔径和液膜位置下的液膜厚度和蒸发质量通量分布示于图5。在其他条件不变的前提下，液膜朝着丝网芯内部后退，接触角上升的同时，传热面积增大，传热传质能力上升，毛细孔能提供的毛细力先上升后下降。因此在输入热流的一定变化范围内，液膜能通过调整自身的位置，在一定范围内契合丝网芯所需的蒸发量和力学平衡，体现了液膜的动态调整能力。但动态调整能力存在范围，而范围的大小取决于工质种类与丝网芯尺寸。

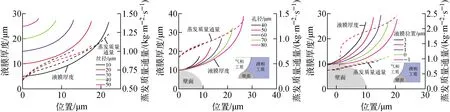
图5 丝网芯尺寸对液膜厚度和蒸发质量通量分布的影响

4 结论

本文基于前驱膜理论和蒸发液膜理论建立了微观液膜模型。通过对运行参数进行敏感性分析，研究了各参数对液膜传热传质与润湿特性的影响。运行温度、过热度和蒸发冷凝系数对接触角基本没有影响，但对热流总量有量级上的影响。运行温度越高，热流总量越高；过热度越大，热流总量越高；蒸发冷凝系数越大，热流总量越高。丝径越大，热流总量越低；孔径越大，热流总量越高。

液膜接触线位置与丝网芯的动态调整能力有关。在液膜在丝网内回退的过程中，毛细力呈先上升后下降的变化趋势。因此在一定热流范围内，液膜在丝网内回退将提升毛细力，从而具有动态调整能力，随输入热流的变化来改变液膜接触线位置，能自动适应所需的蒸发量和力学平衡。但由于毛细力随液膜接触线位置的变化存在拐点，因此在热流较高的工况下，有可能发生液膜接触线位置下降的同时毛细力下降的正反馈现象，导致液膜脱离丝网芯，并发生干涸。

值得指出的是，文献中碱金属薄液膜蒸发实验研究稀缺，因此本文模型采用正辛烷蒸发薄液膜实验结果进行了初步验证。后续将开展液态钠液膜相关的实验研究，结合理论模型进一步探索由于工质变化带来的特殊现象。