定位格架下游湍流特性测量研究
曲文海,陈仕龙,黄慧剑,熊进标
(1.上海交通大学 核科学与工程学院,上海 200240;2.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)
典型压水堆核燃料组件中安装了数个带交混翼的定位格架,既能支撑棒束燃料组件,亦能增强子通道内部和子通道之间的二次流和湍流脉动。子通道程序亟需精确的子通道交混模型[1-2]。CFD模拟是燃料组件设计的重要方法之一,可用于研究格架交混效应,但仍需大量实验数据验证[3-5]。
Xiong等[6-7]使用激光多普勒测速仪测量了3×3和6×6棒束内的三维流场,并讨论了雷诺数效应。Wang等[8-9]在水和氟化乙烯丙烯共聚物(FEP)折射率补偿技术基础上测量了光棒束内轴向流场,并用CFD方法模拟棒束通道内流场。以上研究揭示了光棒束通道内的湍流特征。Nguyen等[10-12]使用基于水和FEP折射率补偿技术的三维粒子成像测速仪(PIV)测量了5×5棒束通道内定位格架下游的流场,获得一个纵截面上三维速度场和湍流特征。Chang等[13-14]使用激光多普勒测速仪(LDV)测量了分流型交混翼和旋流型交混翼定位格架下游横向速度场,获得了交混翼产生的涡结构特征和湍流脉动特征。Li[15]使用水和FEP折射率补偿技术辅助PIV测量定位格架下游的轴向和横向流场,获得了格架下游流场特征。Kim等[16]使用PIV方法和基于有机玻璃与碘化钠水溶液的折射率补偿技术,测量了4×6棒束通道内的纵向速度场。为从光路上消除常规PIV测量中存在的视角误差,Xiong等[17]使用远心镜头测量格架下游横向流场。Qu等[18-20]对基于FEP和水折射率补偿技术的二维PIV方法,进行了系统的误差和不确定度分析,在此基础上获得了定位格架下游的横向流动和湍流沿程变化特征以及雷诺数效应,并开发了滑移式压降测量系统,获得了子通道横向压降。Xiong等[21]基于流场和压降实验数据,开发了子通道交混模型和阻力模型。
在上述研究基础上,本文使用基于FEP和水折射率补偿技术的二维PIV方法,获得不同雷诺数下棒束通道内定位格架下游多个横截面上的高精度精细化横向流场实验数据,分析定位格架下游横向湍流特征和雷诺数效应。
1 实验装置
本实验在上海交通大学中型热工水力回路上开展,该回路包括一个实验回路和辅助的冷却回路。5×5棒束实验段和PIV布置如图1所示,棒直径D=9.5 mm,棒间距P=12.6 mm,子通道水力直径Dh=11.78 mm。三维坐标系定义如图1c、d所示,坐标原点位于格架条带上平面的中心棒圆心,z轴与中心棒轴线重合,正方向沿着主流方向,x轴与y轴沿水平方向。棒束上安装了1个交混翼倾角30°的定位格架,定位格架交混翼的设计参考了文献[22]中的交混翼设计思想,尺寸如图2所示。PIV系统包括1台30 mJ高频激光器(最高频率为10 kHz),1台1 280×800像素高速相机(最高频率为7 400 Hz,像素尺寸dr=20 μm),1台200 mm定焦镜头,1台三维位移平台(行程1 000 mm、1 000 mm、600 mm,精度0.01 mm),1台同步器和1套PIV图像处理软件。示踪粒子为直径dp=20 μm的聚苯乙烯基吡啶树脂(PSP)粒子。实验在暗室中进行,横向速度测量时光学系统图像放大倍数M=0.6,激光面厚度Δz=3 mm。纵向速度测量时光学系统图像放大倍数M=0.4,激光面厚度Δz=1 mm。横向测量面位于z=1Dh~28Dh范围,覆盖中心棒周围的4个中心子通道,横向空间分辨率为0.275 mm。纵向测量面位于y=-1.5P截面上,覆盖z=1Dh~25Dh的范围,空间分辨率为0.32 mm。实验段进口压力为0.15 MPa,温度为25 ℃,4个试验工况的主流平均速度Wb分别为0.5、1、2和3 m/s,对应子通道雷诺数分别为6 600、13 200、26 400、39 600。定义三维坐标系原点于格架条带顶部平面的中心棒圆心处。
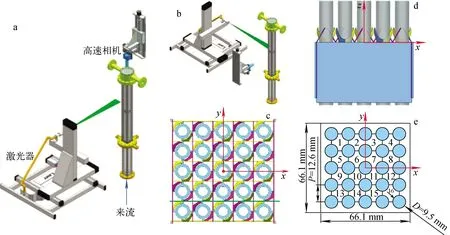
a——横截面测量PIV布置;b——纵截面测量PIV布置;c——纵截面位置;d——格架局部;e——棒束横截面

a——格架尺寸;b——交混翼尺寸
2 实验结果分析
三维平均速度、脉动速度均方根定义如下:
(1)
(2)
(3)
(4)
(5)
(6)
式中:U、V、W分别为x、y、z方向的平均速度;ui、vi、wi分别为x、y、z方向的瞬时速度;N为采样数量;Urms、Vrms、Wrms分别为x、y、z方向的脉动速度均方根。对平均速度和脉动速度均方根以Wb进行归一化。
2.1 误差和不确定度分析
系统误差主要为视角误差和当地速度梯度误差[18],随机误差主要为粒子出平面运动误差,湍流统计量还存在采样数量误差。纠正系统误差后,湍流统计量不确定度由粒子出平面运动误差和采样数量误差决定。平均速度和湍流脉动速度均方根的测量结果最大不确定度小于1%的主流平均速度。
视角误差εp的计算公式为:
(7)
式中:|Vout|为垂直于测量面的速度分量;z0为相机的物距。
粒子出平面运动误差εout的计算公式为:
(8)
式中:Δt为激光脉冲间隔时间,即瞬时速度测量时间;Δz为激光厚度。
平均速度和脉动速度均方根的采样数量误差εN,V、εN,Vrms的计算公式为:
(9)
(10)
为使采样数量误差降低到1%Wb以内,采样数量取为N=5 000。经过系统误差纠正,平均速度不确定度εV由采样数量误差决定,脉动速度均方根不确定度εVrms由粒子出平面运动误差和采样数量误差决定:
(11)
(12)
2.2 横向流场分析
Re=39 600工况下,定位格架下游横向流场如图3所示。在z=1Dh处,1对分流型交混翼在子通道内产生了1对同转漩涡对和绕棒横向速度,U峰值约为40%Wb,V峰值约为30%Wb。随着流动发展,子通道内1对漩涡逐渐耗散扩大融合,在z=5Dh处形成1个覆盖子通道的大漩涡,U峰值约为25%Wb,V峰值约为28%Wb。在z=10Dh处,U峰值约为15%Wb,V峰值约为12%Wb。该漩涡在沿程发展中逐渐减弱消失。在z=28Dh处,U、V峰值约为5%Wb,横向速度分布趋于光棒束充分发展。

a——z=1Dh;b——z=5Dh;c——z=10Dh;d——z=28Dh
纵截面y=-1.5P上的横向速度如图4a所示,相邻两个子通道内正交布置的交混翼片产生方向相反的横向速度。最大横向速度出现棒间隙处,子通道中心附近横向速度较小,横向速度向下游逐渐衰减。在z=1Dh~5Dh区域,横向速度大小显示出子通道内双涡结构转变为单涡结构的现象,随后逐渐耗散。纵截面y=-1.5P上的横向脉动速度均方根如图4b所示,在0~1Dh区域,横向脉动速度均方根分布与交混翼分布一致。在z=1Dh处,横向脉动速度均方根分布与二次流双涡结构一致,Urms有两个峰值出现在子通道内,约为32%Wb。在z=1Dh~5Dh区域,横向脉动速度均方根随着子通道内双涡结构转变为单涡结构而迅速耗散,在z=2Dh处,Urms峰值约为35%Wb;在z=5Dh处,Urms峰值约为15%Wb。随后横向脉动速度均方根缓慢耗散。

图4 Re=39 600时纵截面上的横向速度(a)与横向脉动速度均方根(b)
横向脉动速度均方根分布如图5、6所示,分布模式与涡结构分布一致。在z=1Dh处,横向脉动速度均方根峰值出现在双涡结构处,因为涡结构内强剪切流动产生了强湍流脉动,Urms峰值约为20%Wb,Vrms峰值约为25%Wb。随着双涡结构耗散,横向湍流脉动急剧降低。在z=5Dh处,单涡结构在子通道中心产生强湍流脉动,并逐渐耗散,Urms峰值约为12.5%Wb,Vrms峰值约为12%Wb。横向脉动速度分量呈现出与交混翼分布一致的棋盘式分布。在z=28Dh处,Urms峰值约为4%Wb,Vrms峰值约为3%Wb,横向脉动速度趋于光棒束充分发展分布。
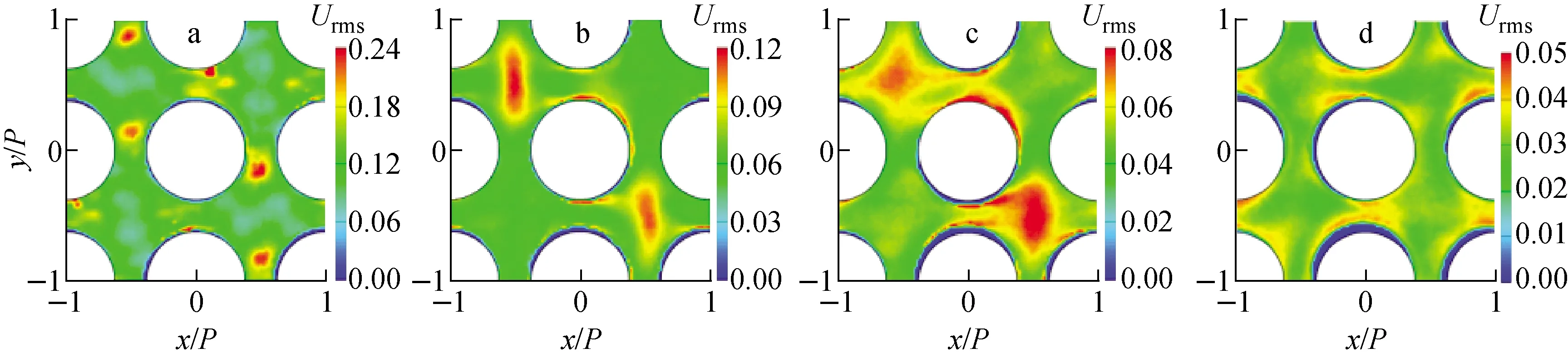
a——z=1Dh;b——z=5Dh;c——z=10Dh;d——z=28Dh

a——z=1Dh;b——z=5Dh;c——z=10Dh;d——z=28Dh
2.3 轴向流场分析
定位格架下游1Dh~12Dh的轴向平均速度如图7a所示。在格架近场,交混翼显著改变了轴向速度分布。在x∈[0,1]范围子通道内,轴向速度在交混翼根部受到指向x轴的交混翼片阻碍显著减小,随后沿着交混翼片方向逐渐增大,在子通道中心(x=0.5P)达到峰值。在x∈[-1,0]范围子通道内,由于交混翼片指向y轴方向,轴向速度未受到交混翼片的阻碍而在子通道中心达到峰值,轴向速度在棒间隙(x=0P)处受交混翼根部阻碍出现谷值。在z=1Dh处,轴向速度峰值位于子通道中心附近,约为117%Wb,最小值位于棒间隙附近,约为85%Wb;在z=2Dh处,轴向速度峰值位于子通道内,约为108%Wb,最小值位于棒间隙附近,约为90%Wb;在z=5Dh处,轴向速度峰值位于子通道中心附近,约为110%Wb,谷值位于棒间隙附近,约为95%Wb;在z=10Dh处,轴向速度峰值位于子通道中心附近,约为105%Wb。
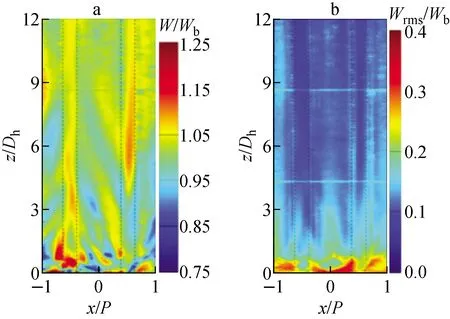
图7 y=-1.5P、Re=39 600的归一化轴向平均速度(a)和脉动速度均方根(b)
定位格架下游1Dh~12Dh的轴向脉动速度均方根分布如图7b所示。在格架近场,轴向脉动速度均方根分布与交混翼方向一致,并在棒间隙附近达到峰值,在子通道中心附近的值较小。随着流动发展,轴向脉动速度均方根迅速衰减。在z=1Dh处,轴向脉动速度均方根峰值在棒间隙处,约为20%Wb,谷值位于子通道中心,约为15%Wb。在z=1Dh~5Dh范围,轴向脉动速度均方根迅速耗散,随后缓慢耗散。在z=2Dh处,轴向脉动速度均方根峰值位于棒间隙处,约为18%Wb,谷值位于子通道内,约为12%Wb;在z=5Dh处,轴向脉动速度均方根峰值位于棒间隙处,约为15%Wb,谷值位于子通道中心,约为10%Wb;在z=10Dh处,轴向脉动速度均方根峰值位于棒间隙处,约为15%Wb,谷值位于子通道中心,约8%Wb。
2.4 雷诺数效应
雷诺数效应如图8、9所示,在格架近场,格架交混效应强于雷诺数效应,掩盖了雷诺数对横向速度的影响。随着流动发展,格架交混效应衰减,雷诺数效应逐渐表现出来。总体上随雷诺数的增加,横向平均速度增大,横向脉动速度均方根减小,并趋于雷诺数无关的自模化区。雷诺数效应对脉动速度均方根的作用更明显。如图8所示,在z=1Dh处,各雷诺数下横向平均速度相差无几;在z=5Dh处,横向平均速度随着雷诺数增大而增大,Re=6 600时最大横向平均速度为20%Wb,而Re=39 600时最大横向平均速度为23%Wb;在z=10Dh处,横向平均速度随着雷诺数增大而增大,Re=6 600时最大横向平均速度为10%Wb,而Re=39 600时最大横向平均速度为16%Wb;在z=28Dh处,横向平均速度随着雷诺数增大而增大,Re=6 600时最大横向平均速度为5%Wb,Re=39 600时最大横向平均速度为7.5%Wb。如图9所示,在子通道中心线y=0.5P上,在z=1Dh、5Dh、10Dh处,横向脉动速度均方根无明显的雷诺数效应。在z=28Dh处,横向脉动速度均方根随着雷诺数的增大而减小。

a——z=1Dh;b——z=5Dh;c——z=10Dh;d——z=28Dh
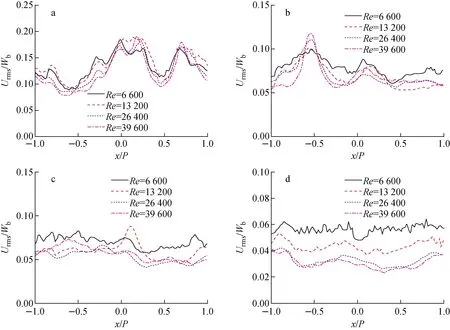
a——z=1Dh;b——z=5Dh;c——z=10Dh;d——z=28Dh
本文实验获得了丰富的横向流场和湍流脉动场的实验数据,能够解释定位格强化子通道交混的机理,能够用于开发精细的子通道交混模型,为子通道分析程序提供基于实验数据库的交混模型,提高子通道分析程序的预测能力和精度。
3 结论
本文使用基于水和FEP折射率补偿技术的二维PIV方法,在4个不同雷诺数下测量带交混翼格架的5×5棒束通道内横向流场,得到以下结论:1)定位格架下游二次流结构经历了双涡结构向单涡结构的转变及单涡结构衰减过程,湍流统计量沿程变化均受涡结构演进影响;2)横向平均速度和脉动速度均方根受雷诺数效应和格架交混效应影响,格架近场以格架交混效应影响为主,格架远场以雷诺数效应影响为主。

