小型无人飞行器的GNSS/INS紧组合观测模型算法

申红雪， 丁国强

(1.郑州轻工业大学 软件学院，河南 郑州 450002;2.郑州轻工业大学 电气信息工程学院，河南 郑州 450002)

0 引 言

将运载体从起始点引导到目的地的技术或方法称为导航[1]，导航系统提供的信息主要有姿态、方位、速度和位置，甚至还包括加速度和角速率，这些信息可用于运载体的正确操纵和控制。随着技术的发展，导航系统的种类越来越多，比如惯导系统(Inertial Measurement Units, IMUs)、卫星导航系统(Global Navigation Satellite System, GNSS)(如GPS)、磁罗盘、里程仪/多普勒测速仪/空速计、气压高度表/雷达高度表、地标点/地图匹配等[2]。这些导航系统各有特色，优缺点并存，如惯导系统的优点是自主性强、动态性能好、导航信息全面且输出频率高，但其缺点是误差随时间不断累积，长期精度差；卫星导航系统的优点是精度高、误差不随时间增大，缺点是导航信息不够全面、频带窄、信号容易受到干扰、在室内等环境下接收不到卫星信号而无法使用。在许多对导航性能要求苛刻的任务中，无论是精度还是可靠性要求高，任何单一的导航系统可能都无法满足要求，这就需要使用多种导航系统同时对运载体进行导航信息测量，再对所有测量信息作综合处理(包括检测、结合、相关和估计)，从而得到更为准确和可靠的导航结果。这种对多种导航信息作综合处理的技术称为组合导航技术。从上述对惯导和卫星导航的优缺点描述中可以看出，两者性能具有非常强的互补性，因而惯性/卫星组合导航被公认为是最佳的组合导航方案[3]，采用多元导航设备，如磁力计、全球导航卫星系统接收机等与IMU组件组合而成的组合导航系统将会为舰船和飞行器等运载体提供更加精确的运载体位置、速度和姿态角信息，能够进一步提高和改善运载体的导航性能[4]。

近几年来关注更多的是基于非线性稳定性理论[5]提出的非线性观测器算法，它具有更好的灵活性，这类观测器模型要求直接的姿态观测信息，或者比较观测向量和参考向量实施姿态计算，其基本原理由文献[6]提出，如文献[7-8]将其应用到导航系统计算中，相比扩展Kalman滤波方法，利用非线性观测器方法的主要优势在于避免非线性系统函数的线性化操作，从而避免非线性函数的高阶截断误差对计算精度的影响；非线性观测器能够获得收敛界，提供稳态收敛保证，观测器整定参数更加直接有效，并且在非线性观测器中，传感器模型噪声经由滤波器参数适当整定后的反馈增益矩阵表达出来，这样做的好处是可以有效控制滤波器带宽。相比扩展Kalman方法[9]，非线性观测器方法对非线性系统状态参数计算具有较好的稳定性能，系统动态模型方程不需要线性化，计算量小，相比MEKF方法，其计算量减小23.6%[10]，在快速机动场合中可以获得较好的实时跟踪效果。

目前GNSS/INS组合有很多种模式方法，相关的文献也有很多，如松组合模式[11]，它利用INS和GNSS的位置组合方法，GNSS提供的位置信息实时修正INS输出的位置量，而更进一步的GNSS/INS紧耦合系统[12]则是利用GNSS导航天文中的伪距和伪距率观测信息实时辅助修正组合系统的注入项，来自于C/A码或者载波相位的伪距信息和伪距率测量信息中包含测量干扰或者误差，如时钟误差、电离层误差和多路径效应等，对时钟误差作为系统状态变量计算，进一步提高系统计算精度，对载波相位测量中引入整周模糊度的固定保持计算方法。

文中提出一种GNSS/INS紧耦合观测器模型方法，利用GNSS伪距伪距率测量辅助INS导航系统，通过构建姿态估计器模型，级联了卫星基座的伪距伪距率平移运动观测器模型，在模型中把卫星和接收机的时钟误差作为系统变量参与计算，提出一种新型的整周模糊度计算方法和伪距伪距率代数解计算方法。由计算机仿真验证，文中GNSS/INS紧耦合观测器模型方法的计算效率高，在巡航导弹制导应用中具有较好的实时性和较高的计算效率。

1 系统传感器配置及其模型

文中主要目标是设计RTK GNSS/INS紧耦合模型系统，估计计算运载体的位置、线速度和姿态信息(PVA)，惯性测量组件安置在载体坐标系(b系)中，卫星测量系统的导航电文提供伪距、载波相位观测量等信息，采用GNSS双接收机模式，一个接收机位于地面站(Base station)，一个接收机固定在运载体(Rover)上，考虑基于固定或者实值模糊度方法计算RTK基线解，并且假设地面站接收机位置是已知固定的，那么卫星广播信号来自于地面基站和运载体接收机两部分。定义载体坐标系b，地球协议坐标系e系(ECEF)和惯性坐标系i系(Earth-centered Inertial Frame, ECI)，那么在地球系中可以获得一组载体动力学方程[13]为

(1)

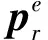
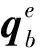
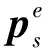
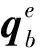
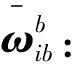
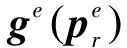
四元数描述导弹载体姿态，如q:=[r;s]，其中r是标量，s∈R3是三维向量，具有范数‖q‖=1；两个四元数的乘积表示为，q1⊗q2，定义为

(2)

对于列向量x，x∈R3，其组成的斜对称矩阵可表示为

(3)

那么两个向量的叉积，如xa，xb，可表示为S(xa)xb。由四元数表达的旋转矩阵表示为

(4)

基于捷联假设IMU组件固定于载体系b中，惯性传感器模型为

(5)

其中bb表示速率陀螺仪偏差，满足条件‖bb‖2≤Mb，Mb是已知误差边界。

磁力计模型描述地球磁场三维向量[13]为

(6)

利用RTK技术要求两个接收机，其中载体中固定的运动接收机观测的GNSS伪距观测模型为

(7)

式中：i——第i个卫星;

yi——伪距观测量；

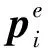
β——待估计的偏差向量，β∈Rn;

ζi——描述了偏差向量元素对距离观测量的影响。

当考虑到Doppler偏移或者GNSS信号跟踪时，需要进一步伪距率观测量，这样做也是为了系统整理组合系统中的偏差误差影响，伪距率观测模型为

(8)

φi——偏差误差向量β元素对伪距率观测量的影响。

从前面的伪距和伪距率观测向量方程可以看到，伪距伪距率方程是非线性的，很有必要从降低计算量角度探究伪距伪距率方程的二次特性来获得相对简化的代数解问题。

(9)

若假设已经获得4个伪距观测向量yi(i=1,2,3,4)，以及3个线性不相关的视线向量，且有

和

且假设对所有的i=1,2,3,4，ζi=1，那么可定义

来给定

其中

(10)

其中

W=diag(1,1,1,-1)，

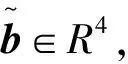
(11)

应该说明的是这里仅考虑缓慢时变系统误差效应，快速变化误差如高频噪声等被忽略，因为快速时变噪声项可由增益整定处理或者高速时变噪声不影响观测器结构。另外注意到伪距率方程在已知观测基站或者接收机位置时成为线性方程，很容易求解计算速度，在典型的伪距观测系统中，其余的观测误差很小，那么利用前面的定理很容易获得观测器的位置和速度初始化，即使有较小的位置和速度初始化误差也是可以接受的，为了计算方便，文中给出载波相位误差假设，在所有时间段内，对所有的卫星i=1,2,…,m，满足

2 非线性姿态观测模型

本模型的计算目标是利用卫星的伪距观测量辅助，在载体系(b系)中的惯性测量组件(IMU)和卫星导航系统组成紧耦合模式，估计载体位置、线速度和姿态信息(Position，Velocity，Attitude，PVA)。卫星导航系统的导航电文提供了伪距、载波相位测量信息。为了计算表达方便,首先定义载体坐标系b系，地球协议坐标系e系和惯性导航坐标系i系，并且标记r代表运动载体，s代表卫星基站。

2.1 姿态观测模型

(12)

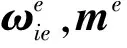
姿态观测四元数误差定义为

‖χ(t)‖2≤κe-λt≤‖χ(0)‖2,

(13)

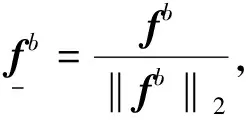
可以表示为

从而注入项表达式可写为

(14)

2.2 平移运动观测模型

引入伪距和载波相位观测方程，φ表示载波相位观测量，单位是m，其与载波周期的关系为

φ=λφcycles，

其中λ表示载波信号的波长，那么第i个卫星的伪距观测量可表示为

(15)

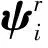
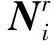
βr——接收机钟差，可以表达为

βr=cΔc;

Δc——卫星与接收机时钟间的时钟偏差；

对于运动载体和基站来说,环境误差都是一样的，因此有

和

考虑运动载体与卫星基站间的单差分观测问题，它们接收第i颗卫星的观测信息，若进一步考虑消除环境误差因素，那么单差分伪距和载波相位观测的差分表达式为

Δρi=Δψi+Δβ,

Δφi=Δψi+ΔΝiλ+Δβ,

(16)

其中

Δβ=βr-βs，

表示运动载体与基站之间的几何基线；消除钟差Δβ的方法可以采用在同一历元中除了第i颗卫星之外的第j颗卫星辅助的二次差分观测方法实现，

∇Δρij=∇Δψij,

∇Δφij=∇Δψij+∇ΔΝijλ,

(17)

其中

∇Δρij=Δρi-Δρj，

∇Δψij=Δψi-Δψj，

∇Δφij=Δφi-Δφj，

∇ΔΝij=ΔΝi-ΔΝj。

实现这样目的关键问题是两个接收机接收到的来自两个卫星的信号是同步性问题，否则卫星与接收机之间的几何距离在观测过程中会发生改变，导致差分观测量不够精确，涉及到卫星信号的整周模糊度计算问题，文献中已经有很多种整周模糊度的计算方法，文中讨论一种称之为“Fixing & Hold”的整周模糊度计算方法。

模糊度计算方法要求卫星基站和接收机至少同时跟踪5颗卫星的信号，m≥5，模糊数可以看作一个复合变量表达为模糊数向量

考虑单差分观测量或者双差分观测量的初始模糊数向量可由前面的伪距误差量和载波相位误差量表达式相减获得

(18)

式中：Δρ，Δφ——单差分伪距观测量;

∇Δρ，∇Δφ——双差分伪距观测量。

利用这两个方程可以平均估计计算在一段时间内历元间的模糊数差分值，但是这两个式子仅可以用于对初始模糊度的估计计算来确定每一个新卫星的星座位置，并且卫星经由一段时间失锁或者遮挡后，再次被捕获时也可以采用这种初始模糊度估计计算方法来确定。

文中把模糊度向量作为观测器状态变量的一部分，可以实现实值模糊度的估计计算，在每一个历元中对模糊度向量估计值进行更新操作，在双差分观测情形中,可以测试模糊度实数估计值由一个整数集合最小化过程是否收敛到一个实数值来检验，如

(19)

(20)

(21)

判断是否成立，若该比率远大于某个阈值，检测结果被接受，那么相应于Ω1的整数被选择出来作为固定的模糊度估计值，则有

(22)

此模糊度检测过程在每一个历元中都会被执行一遍，它利用直到当前历元的所有模糊度数值做出决策，可以做到无遗漏决策判断过程。

考虑载体坐标系b与地球协议坐标系e之间的旋转，以及陀螺仪偏差和加速度计偏差，根据前面假设，在RTK GNSS观测系统中考虑使用双接收机配置，分别列出基站接收机和运动接收机的位置方程，根据前面的位置方程，在位置观测量设计中考虑伪距误差和载波相位误差量的影响，引入运动载体位置量和伪距载波相位误差的相关增益矩阵算子，可以获得相应的位置观测方程；在基本速度方程的基础上考虑运动载体速度观测和伪距误差、载波相位误差的相关增益矩阵算子，可以获得速度观测方程；根据姿态注入项影响，引入辅助变量ξ来构造加速度计比力观测方程[18]，同时把钟差和整周模糊度向量作为系统状态变量设计出它们的观测方程，整个系统模型算法数据流程如图1所示。

图1 GNSS/INS紧组合的姿态平移运动观测器模型

比力估计表达式可由转换运动观测器获得，转换运动观测器方程为

(23)

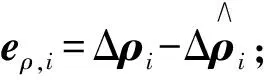
(24)

其中几何距离差分估计项为

(25)

那么观测误差可表达为

(26)

由此引入系统估计误差向量为

(27)

其中

(28)

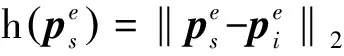
(29)

(30)

利用同样的步骤开展运动载体相关项的Taylor级数扩展逼近计算，可以获得直接的伪距观测误差量的Taylor级数扩展逼近表达式为

(31)

其中

(32)

式中:h.o.t——Taylor级数展开式的高阶项。

在观测增益选择中可以忽略，式(32)中Cρ,i的行向量表达式为

(33)

其中1i,m=[0,…,1,…,0]表示其中第i个元素非零，且有

(34)

由此可以获得系统误差动力学方程为

(35)

其中矩阵

矩阵C是一个2m行的时变矩阵，

C=[Cρ,1;…;Cρ,m;Cφ,1;…;Cφ,m]，

并且式中干扰项定义为:

(36)

(37)

(38)

其中χ是由四元数的向量部分r和陀螺仪偏差b组成的复合变量，

χ=(r,b)，

(39)

同时也应该看到对于一些常数γ3>0来说，满足

‖ρ2(t,χ)‖2≤γ3‖χ‖2

条件。

另外噪声项

ε=(εy,1,…,εy,m;εv,1,…,εv,m)

的线性化结果导致了附加干扰项ρ3(t,x),满足

条件等式。

3 系统Riccati方程的迭代计算过程

转换运动观测器方程可以利用修正-预测方法实施离散化操作，观测器方程组被分成由注入项组成的线性修正部分和非线性预测部分，在IMU采样时预测部分预测计算卫星观测量，预测计算卫星观测量来更新低速修正项部分；在IMU采样中姿态观测量实施欧拉角积分计算。因此整个观测系统误差方程被分成三个时间段开展修正预测计算步骤，其中IMU中姿态观测量和转换运动观测器的预测部分以IMU采样频率速度执行快速计算过程；转换运动观测器的修正部分以卫星导航电文的接收速率来执行，其中在接收导航电文数据中要求获得卫星位置估计数据，可以利用卫星广播星历数据来估计计算。另外，卫星的视线向量随时间变化缓慢，转换运动观测器的增益矩阵K可以较低速率实时更新操作。从降低计算负担角度来说，观测器增益可以数分钟而不是以GNSS接收频率来实施更新操作。

利用前面步骤中已经确定的增益矩阵和方差矩阵来迭代计算离散时变Riccati方程，其步骤分为方差矩阵预测、增益矩阵计算和方差矩阵估计三个步骤完成,

(40)

式中：Ad——矩阵A的离散化表达。

将GNSS频率作为采样频率，系统状态变量为n维，系统状态变量的初始方差为Q>0，观测向量的初始方差阵为R>0，其由伪距噪声方差组成对角元素，观测器可由系统状态变量的初始方差矩阵Q来整定，对应于位置量和线速度量的噪声元素设置得比较小,以利于获得平滑估计，而比力噪声分量元素设置的相对要大，同时最重要的是相应于时钟偏差的元素要设置得足够大,以确保估计操作的快速收敛[18]。根据传感器配置情况，设置系统状态变量噪声方差矩阵

(41)

观测噪声方差矩阵

R=diag{RΔρ,RΔψ,RΔv}。

(42)

4 系统仿真验证

4.1 仿真设置

以六旋翼飞行器作为运动载体，飞行器装备了Xsens MTi 惯性测量组件ADIS 16488 IMU, 它由中等精度的陀螺仪、加速度计以及磁强计组成，其中陀螺仪具有20°/h(1σ)的偏差稳定度，其工作频率是410 Hz；u-Blox LEA-6T GNSS接收机以工作频率5 Hz输出伪距观测量，同时还有一个在地面上相对固定位置的GNSS接收机通过实时动态定位(RTK)计算提供导弹基准位置信息，飞行器上的接收机和地面站接收机具有同样特性，从而构成无人飞行器载体GNSS/INS紧组合观测模型实验测量平台。若在直角坐标系中目标在空中做机动运动，初始时刻相对运动位置为[50 km,60 km,25 km]，相对运动速度为[-18 00 m/s,-1 200 m/s,-500 m/s]，加速度矢量为[5g,6g,8g]，其中g表示目标位置的重力加速度，导弹相对于运动目标的航迹如图2所示。

图2 无人飞行器实验平台

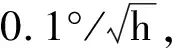
导弹载体观测模型方程中的整定参数可由时变Riccati方程迭代计算获得，设置如下：

k1=0.50，

k2=1.75，

kI=0.008，

kpp=0.06I，

kvp=0.11I，

kξp=0.006I,

θ=2，

λ=0.190 3 m，

其中I表示单位对角矩阵，还有投影算子参数

Mb=0.008 7，

增益矩阵选择为

Kp=diag{0.08,0.04,0.06}。

作为钟差初始值。

4.2 仿真数据分析

无人飞行器运动轨迹数据如图3所示。

图3 无人飞行器运动轨迹数据

由图3可以看出，无人飞行器运动轨迹为比较系统模型算法性能，同时给出GNSS实时测量的估计数据，以及实际测试中的无人飞行器飞行轨迹数据。

系统模型算法计算误差数据和实际测量误差数据比较如图4所示。

实验采用北东地坐标系，由图4可以看出，模型算法计算三个方向的位置误差波动比较小，误差数据收敛快，数据计算稳定性较强，系统模型算法计算获得的路径轨迹数据跟踪实际数据效果比较好。

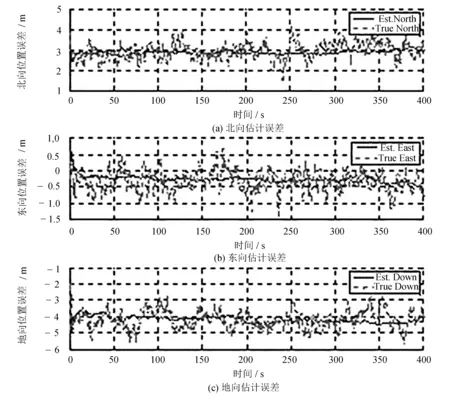
图4 无人飞行器位置误差数据比较

无人飞行器姿态数据比较如图5所示。

图5 无人飞行器姿态数据比较

由图5可以看出，无人机载体姿态角实验数据为了比较方便，显示了实际测试的姿态角数据和系统模型算法计算获得的姿态角数据，特别是利用磁力计测量的航向角数据。

无人飞行器姿态方差数据如图6所示。

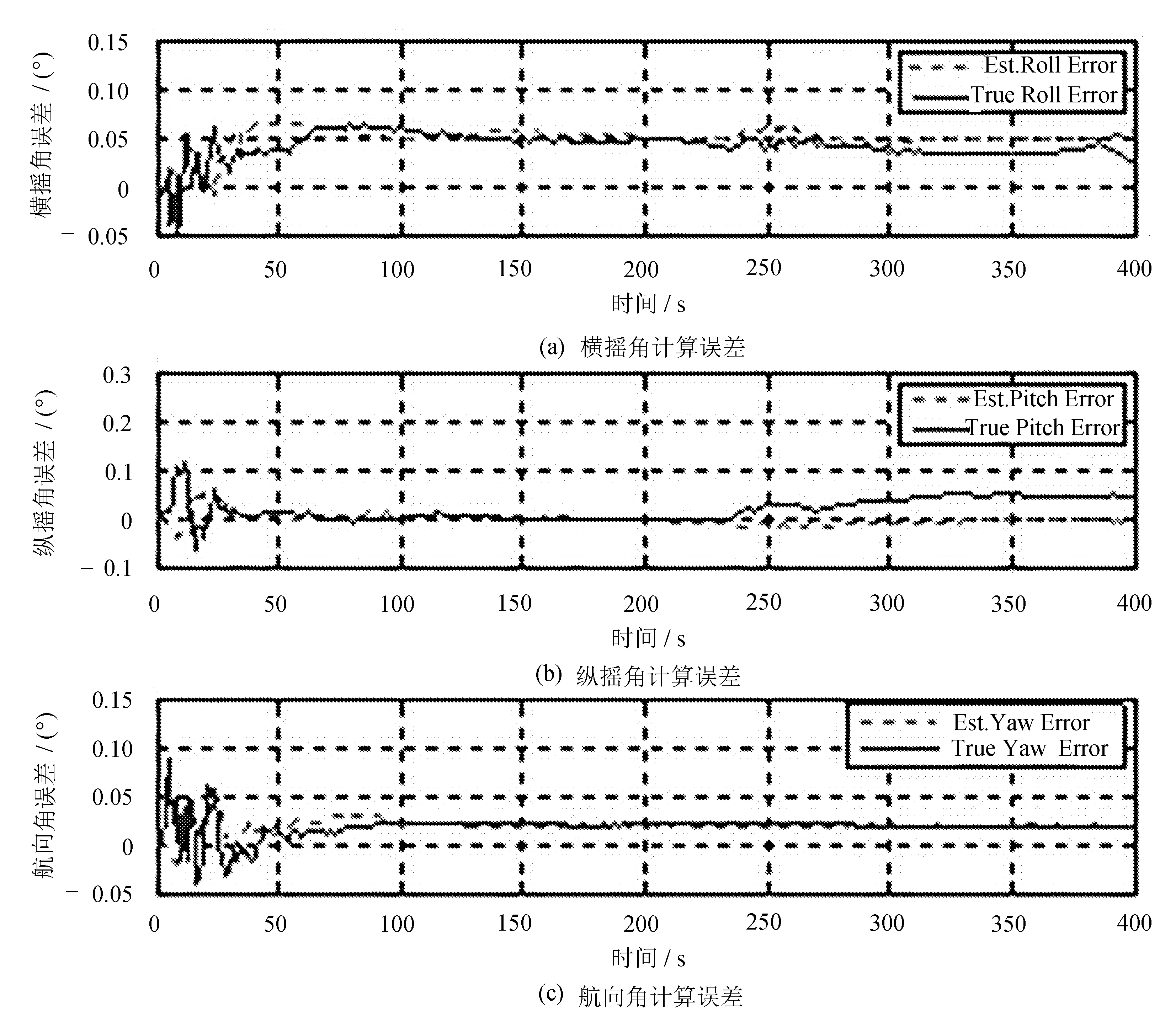
图6 无人飞行器姿态方差数据

由图6可以看出，系统模型算法计算的姿态角误差收敛快，表现出较强的计算稳定性，但是姿态误差角实际测量数据长时间后明显发散。另外与经典的MEKF[19]算法相比，文中提出的多矢量观测模型算法具有较小的计算量，MEKF算法需要经过333 625次乘法和339 770次加法运算，而多矢量观测模型算法仅需要81 738次乘法和63 478次加法就可以完成算法计算流程，计算效率提高23.6%。因此，文中多矢量观测模型算法计算效率高，很适合载体高速机动运动过程中的快速计算要求。

通过数据对比表明，文中提出的多矢量观测模型算法计算效率高，计算精度优于常规算法，特别适合于运动载体高速机动运动场合。

5 结 语

提出一种无人飞行器高速运动载体的RTK GNSS/INS紧组合多矢量观测器模型，基于非线性稳定性理论，利用非平行多观测矢量方法构建运动载体姿态观测器和平移运动观测器模型，模型中充分考虑IMU组件中的陀螺仪、加速度计和磁力计的观测数据及其偏差影响，采用单差分GNSS方法和扩展整周模糊度变量方法获得一种新型的无人飞行器平移运动观测，利用Kalman滤波的预测修正步骤计算系统方差矩阵的Riccati解。经由无人飞行器实验平台测试，文中提出的多矢量观测模型算法计算量小，计算精度满足小型无人飞行器飞行技术要求，验证了文中模型算法的有效性及其在实际使用中的巨大价值。