基于自适应模糊神经网络的氩氧精炼终点碳含量内模控制
马海涛, 姜保良, 吴佳玉, 冯雪雯, 关常君
(长春工业大学 电气与电子工程学院,吉林 长春 130012)
0 引 言
在氩氧精炼低碳铬铁过程中,终点碳含量是整个吹炼工艺的核心,由于冶炼过程高温、多相、环境复杂,存在不可测扰动对碳含量的影响很大,常规控制方法很难达到令人满意的控制效果,作为搅拌作用的氩气,不参加化学反应,但其吹入量会直接影响铁水温度,使铁水温度降低,也会降低一氧化碳分压,进而影响脱碳速率,尽管供氩速率可以测量,但其速率对铁水脱碳速率的影响无法定量估计,所以供氩速率对脱碳过程的影响不可测量。在工业过程中,对于过程扰动无法测量或难以测量这类过程控制,一般采用结构简单、易于在线调节的内模控制(Internal Model Control,IMC)方法,但传统内模控制方法,控制器滤波参数一成不变,导致此方法较难获得理想的控制效果。文中采用一种自适应模糊神经网络的内模控制方法,通过模糊控制器输出在线修正控制器滤波参数,利用结构增减算法优化网络结构,实现规则层神经元动态优化,在线获取一个结构紧凑、泛化性能好的网络,可以获得较好的控制效果[1-3]。
1 控制方案
在氩氧精炼低碳铬铁终点碳含量控制过程中,采用过程扰动无法测量或难以测量这一类过程控制对象较适用的内模控制方法,它具有结构简单、易于在线调节等优点,
针对滤波器参数一成不变,影响控制效果这一弊端,引用一种自适应模糊神经网络控制器,通过模糊控制器的输出在线修正滤波器参数,并利用结构增减算法优化网络结构,实现规则层神经元动态优化,在线获取一个结构紧凑、泛化性能好的网络,可以获得较好的控制效果。
铁水碳含量控制系统组成如图1所示。
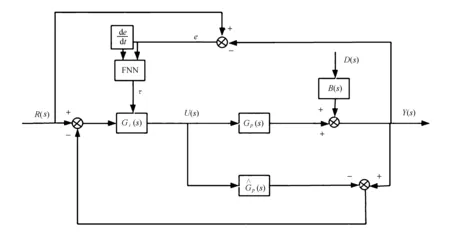
图1 控制系统组成
图中:Gp(s)——被控对象;
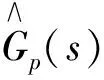
Gi(s)——内模控制器;
FNN——模糊神经网络控制器;
R(s)——铁水碳含量设定值;
Y(s)——铁水碳含量实际输出值;
e——铁水碳含量的期望值与实际值的误差量;
D(s)——氩气对脱碳速率的干扰。
2 内模控制器设计
(1)
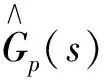
(2)
(3)
(4)
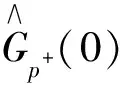

Tf——滤波时间常数。
实际推理控制器形式为
(5)
由图1可以得出,在实际推理控制器的作用下,系统输出为
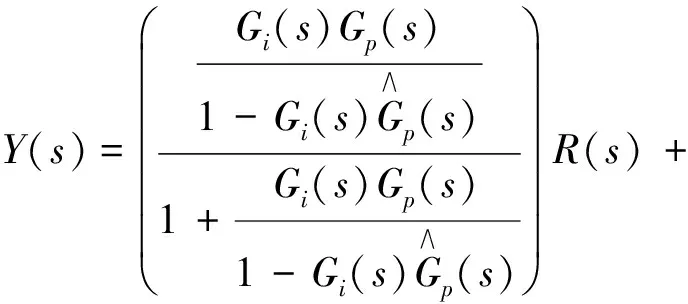
(6)
在模型准确的条件下,系统输出为
Y(s)=Gf(s)R(s)+[1-Gf(s)]B(s)D(s)。
(7)
式(7)中滤波器的稳态增益为1,因而,在设定值阶跃作用下,系统输出的稳态偏差为
R(0)-Y(0)=0。
(8)
在不可测阶跃扰动作用下,输出的稳态偏差为
Y(0)=0。
(9)
系统仍具有很好的稳态性能。
3 自适应模糊神经网络控制器设计
如果在整个控制过程中,滤波器参数值一成不变,势必会影响控制效果,如果仅采用模糊神经网络对滤波器参数进行在线调整,由于冶炼环境复杂多变,参数不变及结构不变的网络无法满足滤波器在线调整要求,文中采用自适应模糊神经网络动态调整内模控制器滤波参数,优化了现有模糊神经网络,优化算法包括两个模块,结构调整模块和参数学习模块,结构调整采用对网络神经元进行增减处理,根据神经元的重要代表性指标,判断其是否被删减,利用激活强度,判断其是否被增添,同时,参数学习方式采用梯度下降法[4]。
3.1 结构修剪算法
为防止神经网络结构处于过度增长,造成冗余,根据生物细胞学,神经元通常不能一直保持兴奋,文中以活跃度为依据,将持续不兴奋神经元舍弃,在线修剪网络结构。假设在初始条件,ρ表示全部神经元不兴奋阈值,重要性值是1。对所有神经元激活强度进行推算时,如果出现修剪阈值大于激活强度的情况,需要对这个神经元进行重要性删减,计算公式为:
(10)
Is (11) 式中:τ——衰减常数; Is——第s个神经元激活强度,初始值为1; Isth——修剪阈值范围,满足Isth∈(0,1); ρ——预设的激活强度阈值,ρ∈(0,1)。 在t时刻,如果预设的修剪阈值Isth大于当前规则层神经元激活强度Is,并且满足式(11),此神经元被删减。 为了避免经过删减的模糊规则干扰神经网络,并且保持网络输出恒定状态,需要对模糊神经网络参数进行补偿处理。在t时刻,假设神经元满足修剪条件,被删减的神经元用s表示。v表示距离此神经元欧几里得度量较小的神经元,新增神经元参数为: (12) (13) (14) (15) v——与神经元s欧几里得度量最小的神经元; cv,σv,ωv——神经元v调整前参数; 将激活强度作为结构增长判别依据,激活强度代表这个神经元对网络调节能力,激活强度大,表示这个神经元对网络调节能力强;反之代表调节能力较弱。如果设定增长临界值大于所有数据对神经元激活强度,则需要对网络结构进行调整,下式为增长评价指标定义,可以满足增添环境变化规则的需求。 (16) 最大激活强度为 (17) 式中:r(t)——此时规则层神经元个数,j=1,2,…,r。 若满足增长条件 Ig 需要增加1个神经元 r(t+1)=r(t)+1。 新增神经元参数被更新为 σnew=σg, (18) (19) (20) 式中:cnew,σnew,ωnew——新增神经元参数; σg,cg——更新后神经元宽度及中心; x(t)——当前输入样本; g——与此时欧几里得度量最小神经元; yr——当前训练样本设定值; y——当前训练样本实际输出值。 仍然采用梯度下降法对改进后网络进行参数学习。 3.3.1 隶属度函数中心值cij更新 (21) (22) 3.3.2 隶属度函数宽度值σij更新 (23) (24) 3.3.3 隶属度函数权值ωpq更新 (25) (26) 4.1.1 自适应模糊神经网络仿真分析 1)初始化推理层宽度、中心和输出权值参数,设定铁水终点碳含量值、修剪阈值Isth、增长阈值Igth、学习率η,规则层神经元个数初始值设定为3; 2)通过100组实验数据训练神经网络,依据式(21)~式(26)更新推理层参数值。网络输入是铁水终点温度实际输出与设定值偏差以及偏差变化率,计算此时网络输出; 3)计算神经元最大激活强度,从而判定此神经元是否满足增长指标,如满足,则增长神经元个数,依据式(18)~式(21)设置新增神经元宽度、中心与权值参数;否则,返回4); 4)根据修剪指标判断规则层神经元是否满足删减条件,如满足,则删除当前规则。神经元参数更新见式(12)~式(15); 5)如果数据训练完毕,则结束循环;否则,返回2)进行重复训练。 采用二阶系统模型验证改进型模糊神经网络的有效性, (27) 采用离线训练得到c,σ,ω参数作为初始值,输入信号为幅值等于2的阶跃信号,采样周期为10 ms,仿真时间为10 s。 将改进型FNN控制器与传统FNN控制器进行仿真对比,仿真结果如图2所示。 图2 对比仿真曲线 图2结果表明,改进型FNN控制器动态性能与稳态性能都优于传统FNN控制器。 4.1.2 控制方法仿真分析 利用Matlab7.0中Simulink创建描述系统输入与输出之间关系模型。将初始碳含量设定为8%,设定目标碳含量为0.5%,一旦铁水中碳含量低于0.5%,则立刻将作为系统输入的供氧速率大小调整为0。氩气流量对铁水碳含量的影响作为系统不可测干扰信号,符合工程实际情况,为体现模糊神经网络内模控制对本系统的适用性,分别采用内模控制、模糊神经网络内模控制对铁水碳含量进行对比仿真分析,数学模型采用所建模型,供氩速率与碳含量关系模型[5-6]为 (28) 供氧速率与碳含量关系模型[7-8]为 (29) 仿真结果如图3所示。 图3 模型匹配下铁水中碳含量IMC与AFNNIMC对比仿真曲线 从图3可以得出,在模型匹配情况下,铁水碳含量控制过程中,自适应模糊神经网络内模控制:调节时间729 s,稳态偏差为0;内模控制: 调节时间939 s,稳态偏差为0。 实验平台采用某铁合金厂为试验基地,以氩氧精炼铁合金所需相关设备为控制对象,以工艺试验参数为依据,由项目组设计研发的一套完整的氩氧精炼铁合金生产过程DCS控制系统,系统包括顶枪供气系统、倾动控制系统、加料控制系统、除尘监控系统、铁水温度在线检测系统等。系统采用二层功能层次结构,选择西门子公司S7-300系列的CPU,以S7300 CPU为核心配以相应的功能模块组成三套完整的独立控制系统,在顶层采用西门子MP377-15触摸屏作为监控中心,与底层各S7-300 CPU通过PROFIBUS-DP与MPI总线组成实时通讯网络,从而实现了分散控制、集中管理与监控的功能,氩氧精炼铁合金DCS控制系统如图4所示。 图4 氩氧精炼铁合金DCS控制系统 为验证文中提出控制方法的有效性,进行了多组冶炼低碳铬铁实验,实验目标为冶炼过程铁水温度不超过炉体最大承受温度1 923 K,以保证炉体寿命,不发生喷溅现象的前提下,铁水碳含量达到0.5%,部分实验结果见表1。 表1 部分实验结果 文中控制方法在保证冶炼过程铁水温度不超过炉体最大承受温度1 923 K的前提下,在冶炼过程不发生喷溅现象,铁水碳含量达到0.5%的终点碳含量误差要求下,缩短了低碳铬铁合金的平均冶炼时长,提高了冶炼效率。 在氩氧精炼铁合金过程中,针对冶炼过程所吹氩气影响铁水脱碳速率,且对碳含量的干扰影响不能在线测量的问题,文中采用自适应模糊神经网络内模控制方法对冶炼终点碳含量进行控制,设计了内模控制器,针对滤波参数一成不变,当数学模型不匹配时,影响系统控制性能的缺点,通过自适应模糊神经网络实时在线调节滤波器参数,改善了系统的控制效果。仿真与实验结果均表明,对于氩氧精炼终点碳含量的控制,文中控制方法具有良好的鲁棒性、抗干扰性能以及目标值跟踪特性,在满足复杂工况生产需求的前提下,提高了冶炼效率。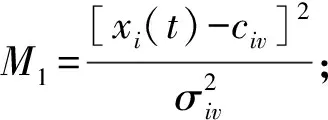
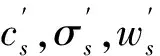

3.2 结构增长算法
3.3 参数学习算法
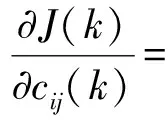

4 仿 真
4.1 仿真分析


4.2 试验研究


5 结 语

