基于NSELPSO 的机械手轨迹跟踪控制研究

齐 港 赵超阳

（广西大学机械工程学院,广西 南宁 530004）

机器人系统是复杂的非线性系统,其具有时变、强耦合和非线性等动力学特性[1]。近些年,将滑模控制、神经网络控制、智能优化算法等方法结合应用到机械手轨迹跟踪控制中,实现轨迹跟踪精度和提高控制器性能已成为机器人领域的研究热点[2-3]。徐传忠等将反演方法与滑模控制结合,设计的控制器减弱了滑模控制的抖振,使滑模控制减少对动力学模型信息的依赖,实现了对关节的轨迹跟踪控制[4]；文献[5]和文献[6]分别使用和声搜素优化算法和权重改变的粒子群算法去优化RBF 神经网络控制器,降低了系统抖振并进一步提高了控制器性能。本文设计了一种基于改进的混合粒子群优化算法（NSELPSO）的神经网络控制器,通过Matlab/Simulink 中仿真对比分析,验证了该控制器对机械手轨迹跟踪的可行性。

1 机械手动力学及控制器介绍

1.1 动力学模型

对于多关节机械手模型,其动力学方程为：

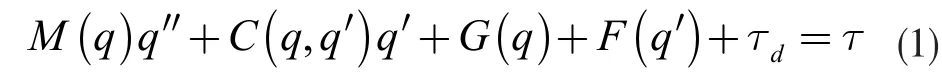
公式（1）中：q∈Rn为关节角位移量,q′和q′′分别是速度和加速度向量,M(q)为机器人的惯性矩阵,C（q,q′）为机器人的哥氏力和离心力矩阵,G(q)为作用在关节上的重力矢量,F(q′)为摩擦力构成的矩阵,τd为建模误差、参数变化和外加扰动等不确定因素构成的矩阵,τ 为控制力矩构成的矩阵[5]。机械手模型如图1 所示。

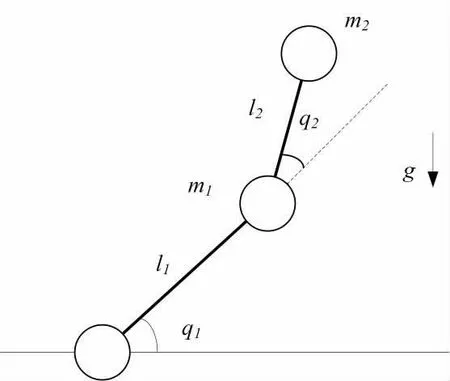
图1 二关节机械手模型

式（1）中：

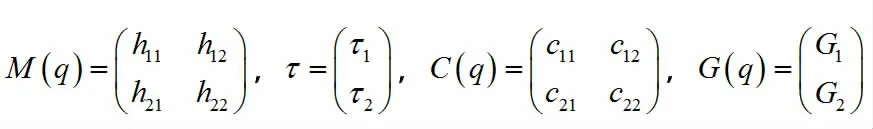
1.2 RBF 神经网络控制器

本文采用RBF（径向基函数）神经网络滑模控制器,设计滑模面函数r 为[7]：

其中, qd为期望轨迹, q 为实际轨迹,滑模面参数Λ为元素均正的对角矩阵。

结合式(1)和(2)易得：

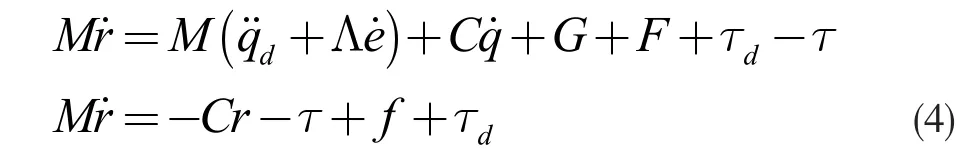
其中,

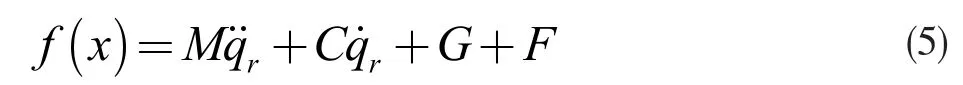
由式(5)可知,f(x)含有关于机械手模型中动力学方程的所有信息,本文通过RBF 神经网络对该模型的f(x)进行逼近。

采用RBF 网络对f(x)逼近,网络算法为：

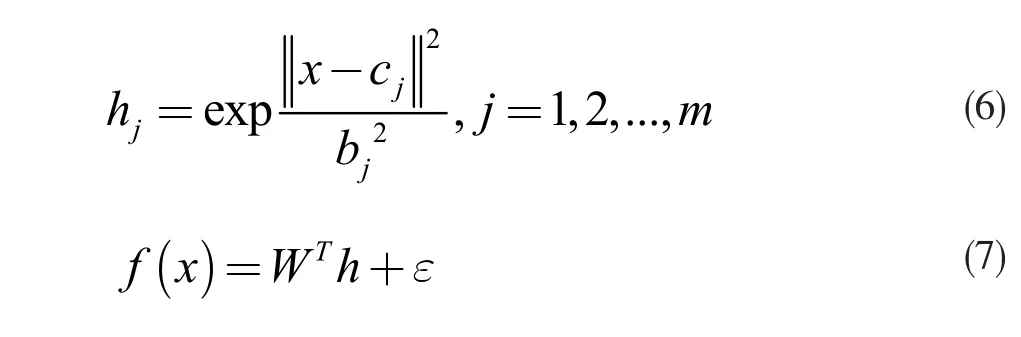
其中x 是网络的输入向量,W 是理想的权值,ε 是一个很小正数,h=[h1,h2,...,hm]T是隐含层输出向量。

2 优化实现

2.1 优化原理

改进混合粒子群算法（NSELPSO）的原理是在基本粒子群迭代后将粒子按照适应度值进行排序,将种群中位置和速度最好的一半粒子去替换种群中最差的一半粒子,仍保留粒子中原始最优适应度值[8]。

在RBF 神经网络去逼近非线性函数时,式(6)中控制参数b 和c 的选取对网络的逼近效果影响很大,若两个参数选择不合适,高斯基函数就得不到有效映射,使得网络逼近失败。因此,本文基于混合粒子群算法对控制参数b 和c 的选取进行优化,提高控制器的轨迹跟踪效果。优化流程图如图2 所示。

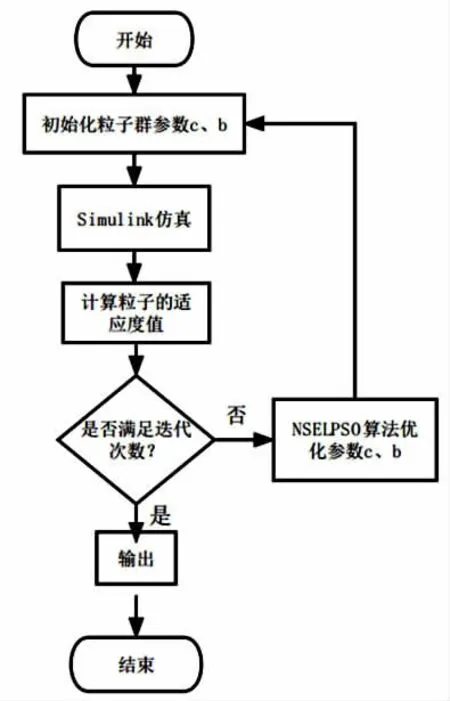
图2 控制器优化流程图

2.2 优化过程

设置控制参数c 中元素寻优范围（-3,3）,b 中元素范围（0,15）,定义适应度函数E 为整体逼近输出和实际输出的相对误差绝对值总和：

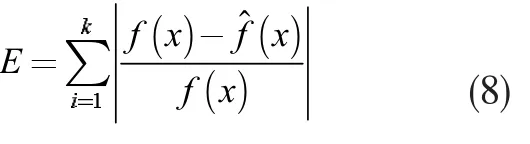
选取粒子数为40,优化迭代300 次,选择与文献[9]的参数设置进行对比,最终经NSELPSO 优化后参数设置为：

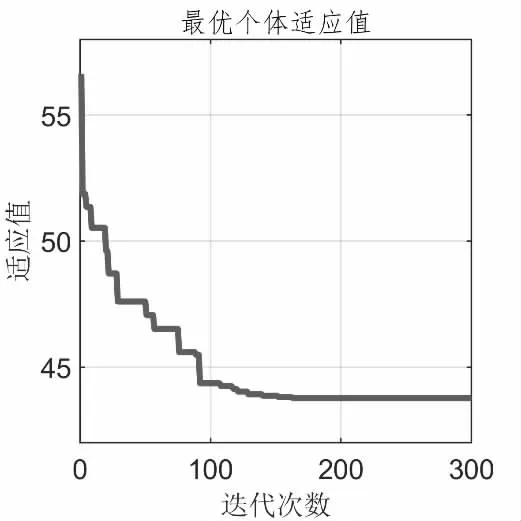
图3 迭代曲线

3 实验和讨论

以式（1）的动力学方程为控制对象,其参数设置为：

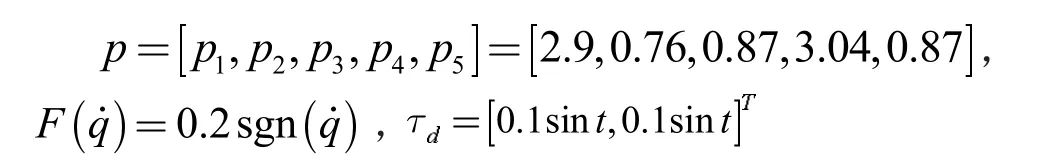
选取2 个输入向量,7 个隐含层输出向量,1 个输出的RBF 神经网络结构,输入为z=,网络初始权值为0,理想跟踪轨迹为q1d=q2d=0.1sint,初始状态

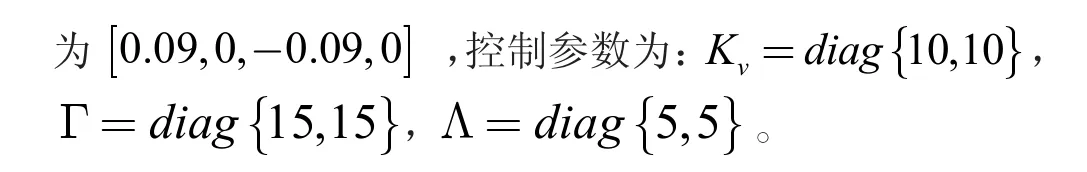
对比分析分别利用改进混合优化算法（NSELPSO）和基本粒子群算法（PSO）对机械手的轨迹跟踪控制效果,仿真结果如图4、5 所示。

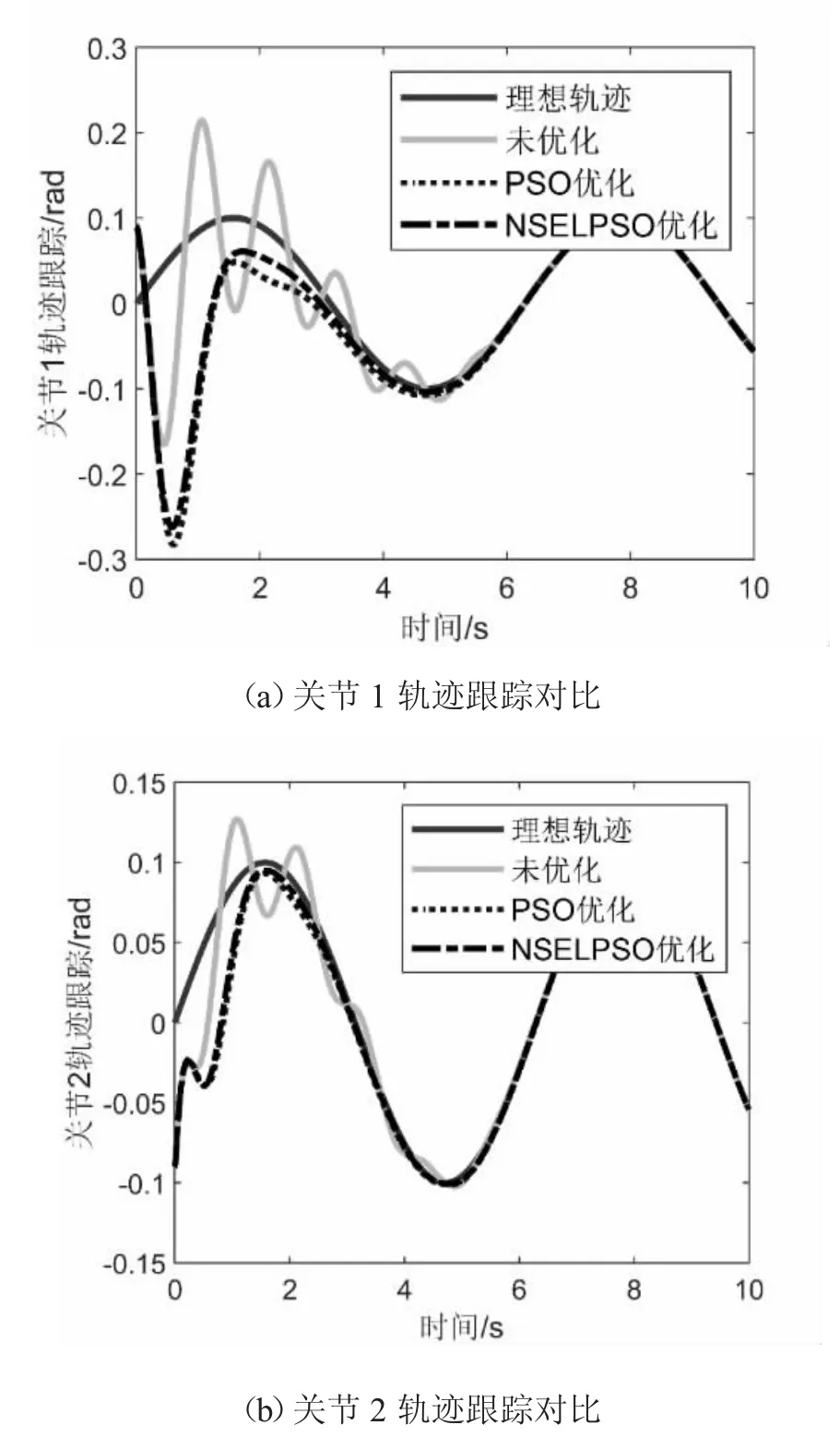
图4 关节跟踪轨迹仿真对比

由图4 可知,经优化后的神经网络控制器对关节的轨迹跟踪精度得到了很大提高,本文提出的NSELPSO方法则进一步提高了关节轨迹跟踪精度。由图5 可知,虽然被优化后的控制器受到关节角速度跟踪误差的影响起始跟踪误差比较大,但误差收敛时间明显提高了。并且用NSELPSO 方法优化后的控制器关节跟踪误差减小,且更平稳、更快地收敛。

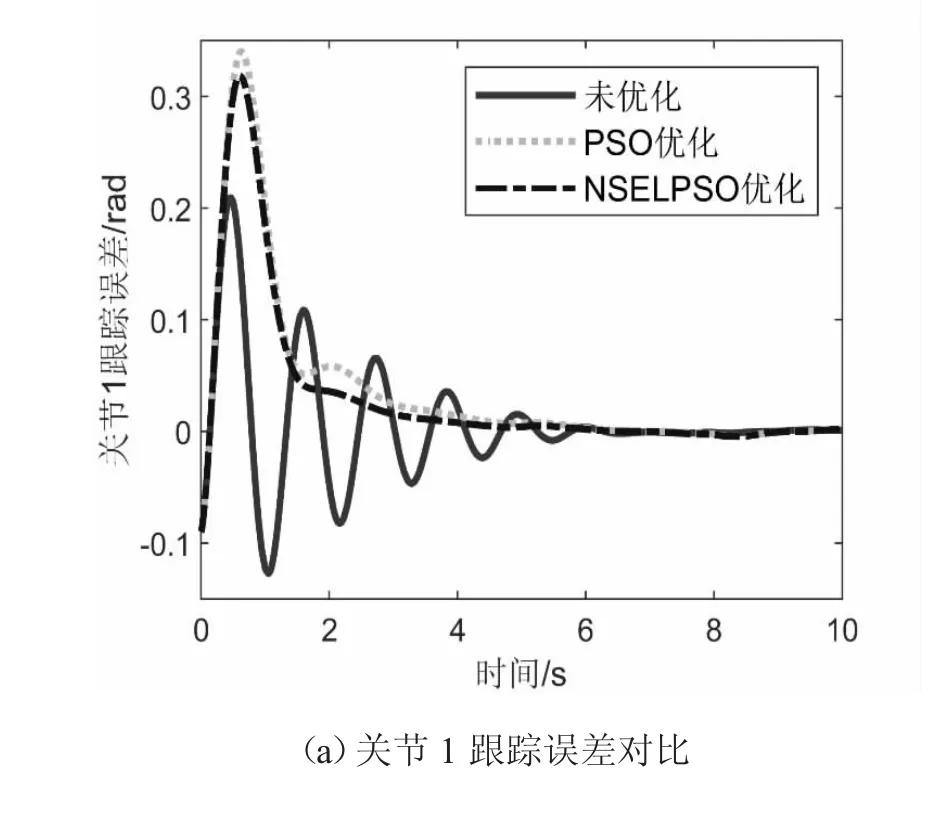
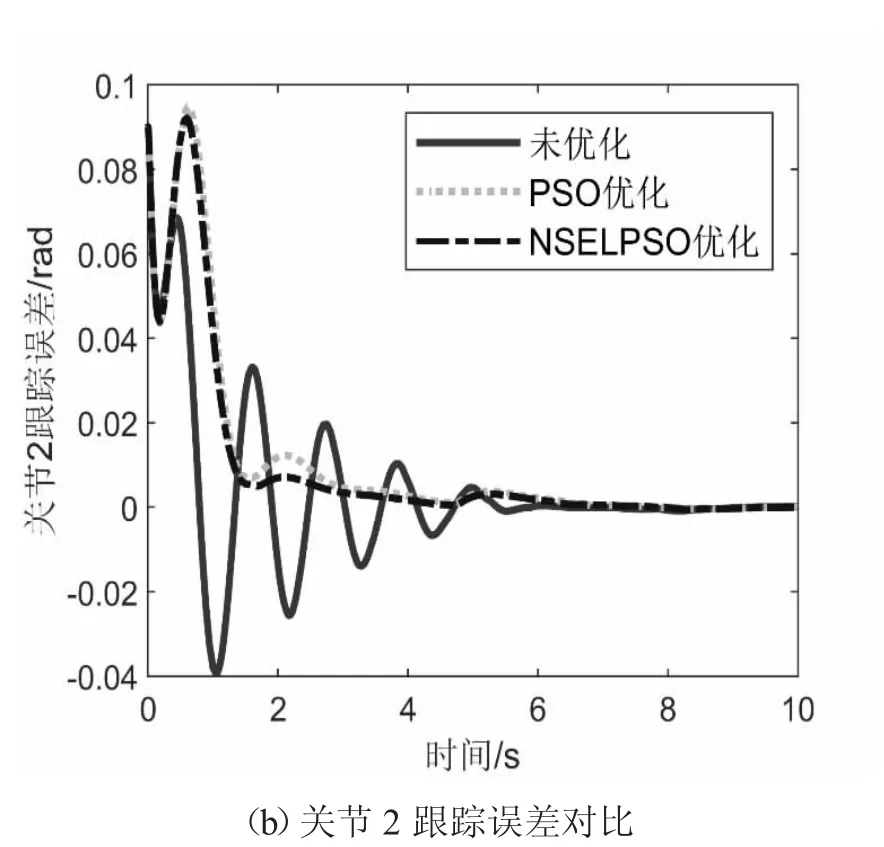
图5 关节跟踪误差仿真对比

4 结论

4.1 本文提出了一种结合混合粒子群算法的RBF 神经网络滑模控制器,通过算法优化神经网络的控制参数,提高了对机械手模型不确定项的逼近能力,进而提高了控制器性能。

4.2 阐述了一种RBF 神经网络控制器的优化实现原理,并在此基础上运用了改进的混合优化算法实现了控制器的优化。在仿真结果上,与未优化控制器和用单一算法优化的控制器,NSELPSO 算法优化效果更明显。

由仿真结果可见,采用改进混合粒子群算法优化后的控制器具有较好的轨迹跟踪性能, 并削弱了滑模控制系统中存在的抖振现象。