基于小波神经网络的暖通空调系统短期热负荷预测

李明柱，纪田雨，李亚男，陈灏馨

吉林建筑大学 市政与环境工程学院,长春 130118

0 引言

根据国际能源署(IEA)统计,建筑业已成为世界最大的能源消费行业,占世界最终能源消耗的32 %[1].中国建筑运行的总商品能耗约占全国能源消费总量的20 %[2].由此可见,建筑节能在暖通空调领域的潜力很大.短期(即预测时间小于1周)负荷预测是建筑节能的基础[3-4].暖通空调系统需要精确的负荷预测来指导运行优化[5]、诊断系统故障[6].目前,对短期冷负荷预测方法的研究大致可分为基于物理模型的方法和基于数据驱动的方法两类.基于物理模型的方法依赖于物理原理和建筑及其系统的详细信息来表征建筑热行为.物理模型可以捉拿实际的建筑热响应的各种影响因素,但它需要大量详细的建筑信息(如建筑围护结构信息和建筑设备的选择),如物理原理的假设得不到满足[7],模型的性能可能就不一致.而基于数据驱动的方法主要依靠建筑物的运行数据来发现建筑负荷与相关变量(如室外温度、室外相对湿度、室内占用率等)之间的关系,以这种方式开发的模型被称为灰盒模型[8]或黑盒模型.以往研究表明,机器学习和人工智能领域的预测技术,如支持向量回归[9]和人工神经网络[4,10],在建筑能耗预测中取得了较好的效果.各种研究也表明,与线性方法相比,如多元线性回归、自回归滑动平均模型等非线性方法可以获得更准确的结果[11-12].数据驱动模型,特别是黑盒模型的主要优点是建模过程更加高效和灵活.已有国内外学者运用神经网络来预测建筑负荷[13-15].由此可见,人工神经网络(Artificial neural network,缩写ANN)预测建筑负荷已有广泛的应用.Li等[16]人对反向传播(BP)算法神经网络、径向基函数(Radial basis function,缩写RBF)神经网络和广义回归神经网络(General regression neural network,缩写GRNN)3种神经网络冷负荷预测精度进行了对比,其中BP神经网络中Sigmoid函数不能保证解的唯一性,且Sigmoid函数不能定量地确定逼近所要求的分辨尺度,故BP神经网络的设计具有盲目性.国内外学者希望建立一个能够克服Sigmoid网络缺陷的神经网络.小波神经网络(Wavelet neural network,简称WNN)由此产生.

数据驱动方法的预测精度主要由作为模型输入的变量和用于模型开发的预测技术的两个因素决定.由于暖通空调系统负荷呈现较强的随机性和非线性,输入变量需要不同规律的叠加.小波变换利用多尺度分析特性将负载信号分解成多个频段信号,可提高输入变量的数据质量.近年来,小波变换已与支持向量机结合来预测暖通空调系统的负荷.周旋等[17]人结合小波分解(Wavelet decomposition,缩写WD)与支持向量机(Support vector machine,缩写SVM)对办公大楼负荷进行预测,所获结果与仅用支持向量机(SVM)预测结果相比,小波分解-支持向量机(WD-SVM)法预测精度比支持向量机(SVM)法的预测精度提高了33.6 %,其原因是小波变换提高了预测精度.

本文拟提出基于小波神经网络(WNN)的暖通空调系统热负荷预测模型,其模型预测过程是利用小波分解法先把初始热负荷信号分解成低频信号和高频信号,然后再对分解后的各分量个别地进行人工神经网络预测,最后通过不同频带的预测量值来重构小波,并获得热负荷最终预测值.

1 小波神经网络

1.1 小波分析原理

小波分析是统筹时域和频域局部化分析方法,通过对小波函数进行伸缩平移对信号进行多尺度精细化分析,获得反映原始信号变化情况的高频信号和反映原始信号变化规律的低频信号.小波分析具有使用各种不稳定信号的灵活性.用于小波变换的小波函数ψ(x)具有振动特性,能迅速衰减为零,其定义见式(1).

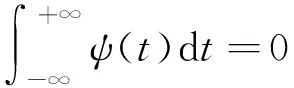
(1)

小波分解可将离散数据(冷热负荷数据是离散的)转换成不同频率的多个频带的信号,低频信号反映了原负荷的基本变化趋势和变化规律,高频频带反映了原负荷的随机变动状况.小波分解法的分解式为S=A3+D3+D2+D1,其分解过程如图1所示,即将初始信号

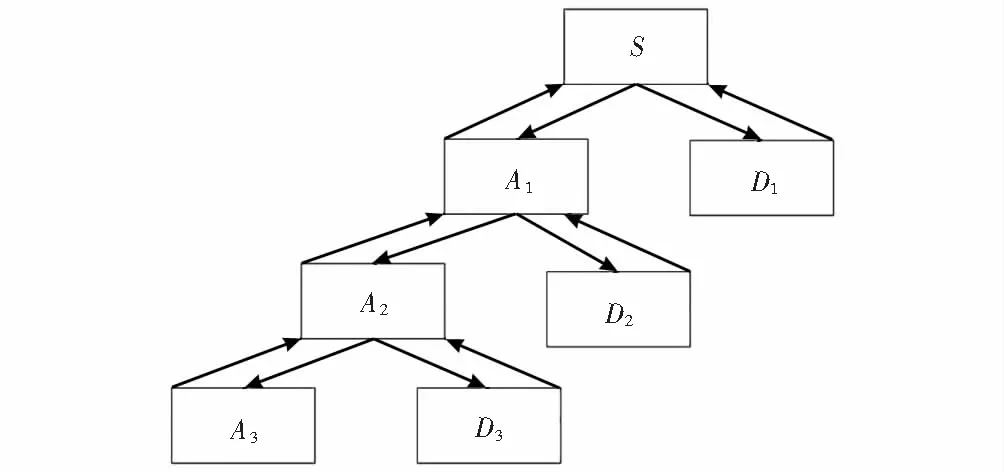
图1 小波分解与重构原理Fig.1 Principle of wavelet decomposition and reconstruction

S分解成1个低频信号A1和1个高频信号D1.高频信号D1不再分解,低频信号A1再次分解得到1个新的低频信号A2和高频信号D2,分解过程持续至出现新的、平滑的低频信号为止.信号f(x)的离散小波定义由下式给出：

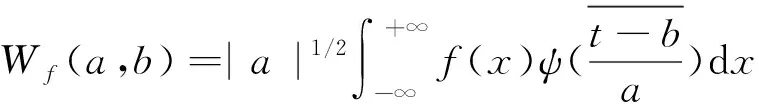
(2)

式中，a为尺度参数;b为平移参数.

由预测模型获得对应的预测值后,如不对不同频带信号的预测值进行小波重构,则不能得到最终的预测值.高频带的预测值D3′和低频级的预测值A3′被重构为A2′,重构过程持续至A1′和D1′被重构且获得信号的预测值S′为止.信号f(x)的离散小波逆变换定义由下式给出：

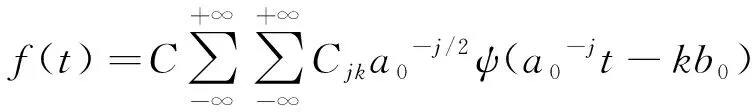
(3)

式中,C为常数;Cjk为小波变换系数;a为尺度参数;扩展步长a0≠1是固定值;b为平移参数;b0为平移参数初始值;j∈Z.

1.2 人工神经网络

人工神经网络模仿人脑的工作原理执行学习和预测任务.神经网络是基于生物学有着与人类神经系统相似的构造.反向传播神经网络(Back propgation neural network,缩写BPNN)是目前应用最广泛的多层人工神经网络.从输入层到隐藏层以前馈方式连接到输出层的BP算法的设计目标是使预测输出和期望输出间的均方误差最小化.本文采用3层BPNN,由输入层、隐藏层和输出层构成.输入层接收来自外部源的信息,并将该信息传递到网络以进行处理；隐藏层从输入层接收信息后,进行所有的信息处理;输出层接收从网络处理的信息,并将结果发送给外部接收器，其原理如图2所示.

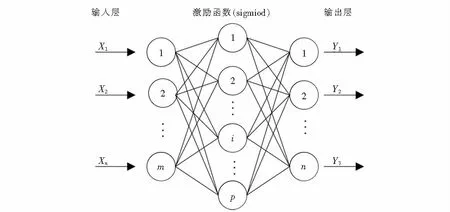
图2 BP神经网络原理Fig.2 Principle of BP neural network

输入层神经元的输出表示为:

Oij=Xij,i=1,2,…,nj=1,2,…,m

(4)

隐藏层神经元的输出表示为：

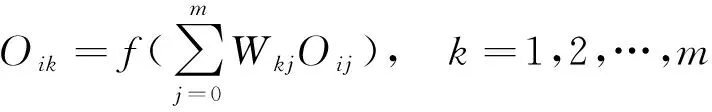
(5)

输出层神经元的输出表示为：

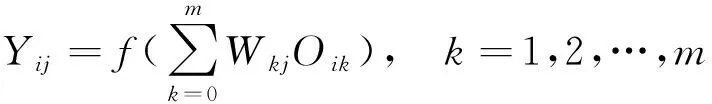
(6)

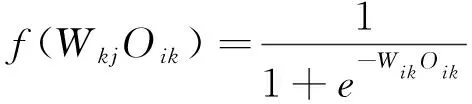
(7)

式中,Xij为神经元输入;Oij为输入层神经元输出;m为隐藏神经元数,个;Wkj为第j个输入神经元到第k个隐藏神经元的连接权值;Oik为隐含层神经元输出;f(wkjOik)为Eq给出的sigmoid传递函数;Yij为神经元输出.

1.3 小波神经网络

WNN是基于小波分析理论构成的分级、多分辨率的人工神经网络模型.也就是说,用非线性小波函数代替正常非线性激发函数(例如Sigmoid函数),并从相应输入层到隐藏层的权重和隐藏层的阈值分别由小波函数的比例伸缩系数和时间平移系数代替，小波网络充分结合了两个优点，能够避免陷入局部极小值收敛速度快，并可对输入变量进行时间频率局部分析,其原理如图3所示.

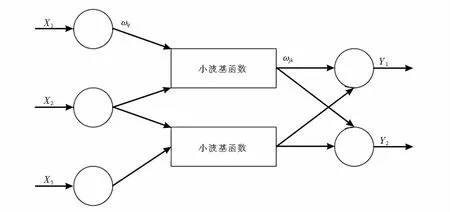
图3 WNN原理Fig.3 WNN Principle

2 基于WNN的暖通空调系统负荷预测模型

2.1 数据来源

本文以吉林省图书馆的暖通空调系统为研究对象.该图书馆占地面积45 000 m2,总建筑面积53 400 m2,地下1层,地上5层,采用“地源热泵+备用电锅炉+城市集中热力网补偿”的复合源热泵系统为建筑物冬季供暖夏季供冷,其中夏季冷负荷4 140 kW，冬季热负荷4 820 kW.

本系统采用4台麦克维尔WPS450.3C单螺旋杆式热泵机组,备用电锅炉2台对建筑物进行冬季供暖,冬季工况辅助热力网进行调峰;夏季供冷开启3台热泵机组.为调节平衡地下土壤源温度场,夏季工况时采用3台换热量为1 100 kW的翅片式热补偿器向土壤层中补充热量,以平衡季节性冷热负荷.

热负荷预测样本由训练样本和测试样本两部分组成,其中训练样本为长春典型气象年2016年1月26日至2月18日的气象数据及其模拟负荷计24天17 280个样本数据、测试样本为2016年2月19日～24日实际气象数据及其模拟负荷计6天4 320个样本数据.以下所述实际负荷的平均值为DesignBuider软件构筑事例建筑模型的模拟结果.以20 min/次的频率收集该系统的数据,包括记录在传感器中的复合源热泵系统在内的各种运行数据,本文以复合源热泵机组为对象进行热负荷预测.

2.2 数据预处理

数据分析之前,要将数据归一化,对处理后的数据进行分析.由于原始数据中存在一部分异常值,故为了不影响数据的时序性,需剔除数据中的异常值,本文采用零值填充的方法补全.

对数据进行标准化处理,其目的是使得预处理的数据被限制在一定的范围内,消除奇异样本数据产生的不良影响.数据经归一化处理后,可加快收敛速度.本文采用最大-最小标准化对原始数据进行线性变换即原始值x通过最大-最小标准化映射到[0, 1]区间,得到标准化后的值x′,其表达式为：

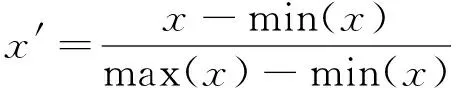
(8)

式中，x′为标准化后原始数据;x为原始数据;max(x)为原始数据中最大值;min(x)为原始数据中最小值.

预处理后的数据用于小波分解和训练建模，数据处理结果见表1和图4，数据处理过程使用软件IBM SPSS Statistics 24.0,描述性统计表为SPSS导出结果.

表1 热负荷数据和归一化处理数据描述性统计Table 1 Descriptive statistics of heat load data and normalized processing data

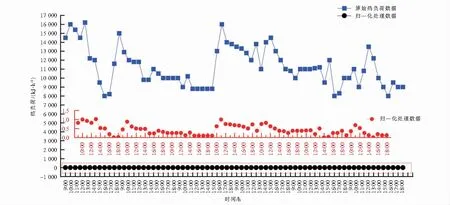
图4 原始热负荷数据预处理结果Fig.4 Preprocessing results of original heat load data

2.3 训练建模

在得到预处理的能耗序列数据后,对原始能耗数据进行小波分解(小波分解尺度选为2级,小波基函数采用db4),对A3,D3,D2和D1分别构建基于WNN的训练模型.根据数据集的划分,取前80 %(17 280个)的数据作为训练集,取剩余的后20 %(4 320个)的数据作为测试集;将训练集的数据输入WNN模型,获得了复合源热泵机组的热负荷预测模型,其预测流程如图5所示.

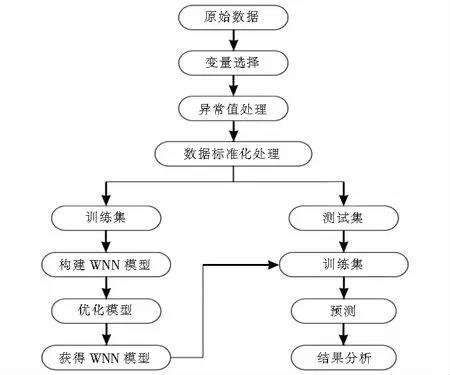
图5 WNN模型预测流程Fig.5 WNN model prediction process

2.4 负荷预测评价标准

本文以平均绝对误差(Mean absolute error,缩写MAE)和均方根误差(Root mean square error,缩写RMSE)作为反映模型预测值与真实值之间误差实际情况和衡量预测值与真实值之间偏差的评价指标.

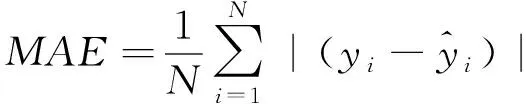
(9)

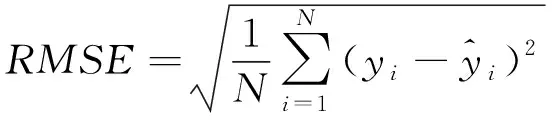
(10)

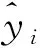
3 预测结果与分析

3.1 小波分解结果

很多研究表明,DbN小波基函数适用于分析时序问题,故本文采用DbN小波基函数进行分解.小波分解时需有合适的小波基函数及小波分解尺度.通常情况下,消失差距(N为小波消失矩)越大,高频系数愈小,小波分解后的图像能量越集中,正则性(函数平滑度)越好，小波分解后的效果会更好.因此,小波的正则性和紧迫性是相矛盾的.图6为2月1日～7日初始热负荷信号逐时变化曲线,图7为2月1日～7日Db1～Db5小波基函数下低频段热负荷逐时变化曲线.

图6 2月1～2月7日间初始热负荷信号逐时变化曲线Fig.6 Hourly change curve of the initial heat load signal during February 1～7

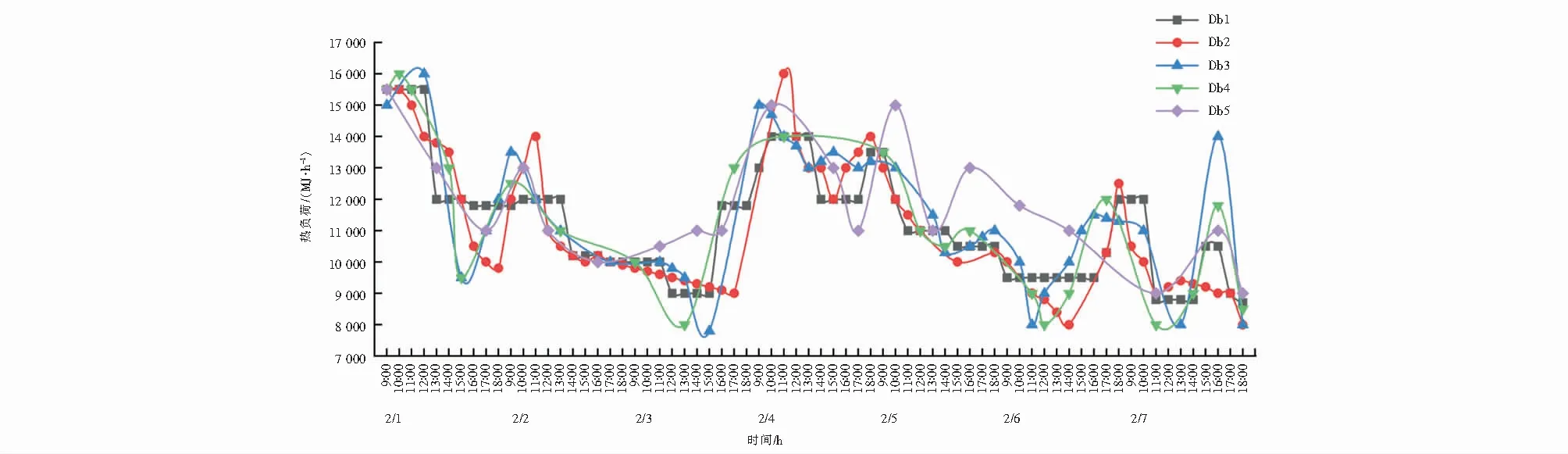
图7 2月1日～2月7日间Db1～Db5小波基函数下低频段热负荷逐时变化曲线Fig.7 Hourly change curves of thermal load in low frequency band under db1-DB5 wavelet basis function during February 1～7

小波基函数DbN的N越大,小波分解的平滑度和定位能力越好,意味着可更有效地监视奇异点.但是N值过大,会产生模糊的分析结果,计算量也会增加.图7显示,使用Db1,Db2和Db3小波基函数时,低频段曲线不平滑.另外,初始信号曲线的形状也有一定程度的破坏.如使用Db4小波基函数,低频段曲线会变得十分平滑,能很好地反映初期信号曲线的变化倾向.如再增加N值,低频段曲线的变化会减小，这表明没有持续增加的意义.因此,本文选择Db4小波基函数,对初始热负荷信号进行小波分解.图8为2月1日～2月7日小波基函数Db4下1～4级分解尺度的低频段热负荷逐时曲线.

图8 2月1日～2月7日期间小波基函数Db4下1～4级分解尺度的低频段热负荷逐时曲线Fig.8 Hourly variation curves of thermal load in low frequency band at the level 1～4 decomposition scale under wavelet basis function Db4 during February 1～7

在小波分解过程中,小波分解尺度不能过大或过小.当小波分解尺度过小时,无法完全有效地提取初始信号不同频带的信号;而当小波分解尺度过大时,如小波分解比例过大,各模型都会引入一定的误差,最终重建结果可能会产生较大误差.

小波分解尺度定为1级时,低频段曲线不会充分平滑，小波分解尺度定为3级或4级时,低频曲线的形状会被破坏.如将小波分解尺度定为2级,则低频段曲线保持初始信号曲线的周期性,非常平滑,从初始信号中提取的信息也足够.因此,本文对热负荷序列进行小波分解时,将小波分解尺度定为2级.

3.2 模型预测、训练测试结果分析

图9为2月23日WNN模型预测热负荷、BP模型预测热负荷和实测热负荷逐时变化曲线.图9表明,WNN模型和BP人工神经网络模型对热负荷的预测整体表现出较高的准确度,10∶00时之前上述模型的预测值与实测原始数据误差较大,10∶00时及其之后则拟合度较好.通过两种模型的对比,表明WNN模型的预测值与实测原始数据误差整体小于BP模型且较稳定.取前 80 %(17 280个)的实测原始数据作为训练集,取剩下的后20 %(4 320个)的实测原始数据作为测试集,由式(9)～式(10)算得两种模型预测热负荷的平均绝对误差MAE和均方根误差RMSE,见表2.由表2可知,WNN模型的MAE和RMSE均小于BP模型的对应指标,其预测精度高于BP模型预测精度.因此,在应用了数据多尺度分析之后,小波分析可从实测原始数据中提取更多的有效信息.

图9 2月23日WNN模型预测热负荷、BP模型预测热负荷和实测热负荷的逐时变化曲线Fig.9 Hourly variation curves of WNN model forecast thermal load,BP model forecast thermal load and measured thermal load on February 23

表2 WNN和BP模型预测短期热负荷的MAE和RMSETable 2 MAE and RMSE of short-term heat loads forecast by WNN and BP models

4 结论

(1) 小波神经网络充分结合了小波分析和神经网络的优点,即逼近能力强、收剑速度快、网络参数(隐层节点数和权重)的选取有理论依据,有效避免局部最小值.

(2) 本文采用改进后的反向传播(BP)神经网络也亦WNN来构造出相应的预测模型,并对WNN 和 BP神经网络模型的预测结果进行了分析.结果显示,基于WNN模型的预测值的MAE和RMSE均优于BP模型,预测值与实测值拟合得很好,MAE为8.537,RMSE为12.936,具有较高的预测精度,其精度已明显优于单纯的BP神经网络模型.由图8可以看出,小波网络模型的预测精度较高,具有较好的学习性和鲁棒性.

(3) WNN对暖通空调系统热负荷提前24 h预测,能显著提升预测精度,便于实时调节暖通空调系统运行策略,达到建筑节能的目的.