让作业融合学习

李国瑛

“双减”背景下，作业已从传统意义的课后训练，发展成为教师引导学生开展自主学习、承载学习内容、体现学习方式、实施过程性评价的具有独立意义的学习活动，即作业要融合到学习中。在教学实践中，笔者对教学内容深度加工，将它转化为能引发学生深度学习的学习材料，借助学习单，通过独立探究作业、合作分享作业、拓展与挑战作业等不同形式的作业，引导学生经历丰富多彩的深度学习活动，从而发展数学学科素养。下面，笔者以北师大版教材数学四年级上册“乘法分配律”一课为例，来阐述将作业融合到学习中，帮助学生经历知识的形成与建构过程。

一、复习作业，初步感悟

在解读教材时，笔者思考：学生的现有水平是什么？未来要达到的水平是什么？从而根据学生的最近发展区，以学习单的形式设计可以帮助学生与自我认知基础对话的作业。

师：孩子们，我们前两节课学习了乘法的两条运算定律，分别是乘法交换律与乘法结合律。其实乘法还有一条重要的运算定律——乘法分配律（板书：乘法分配律）。

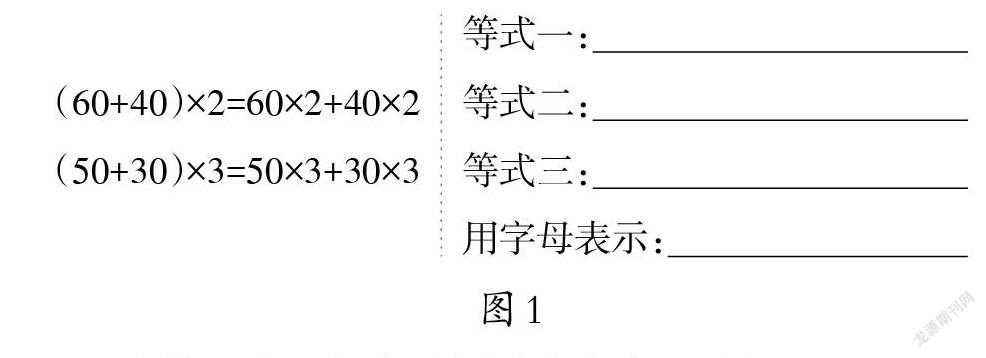
课件呈现学习单中的复习作业：运动会前，老师去购买运动服，一套男装（上衣60元、裤子40元），一套女装（上衣50元、裤子30元）。问题1：买两套男装需要多少元？问题2：买3套女装需要多少元？分别用两种不同的方法解答，完成后与同桌互相批改并分享列式解答的理由。

学生独立完成后教师请一个学生带上自己刚才完成的学习单来分享。

生（通过实物投影仪展示学习单，边分享边在学习单的算式下面画线）：我是这样想的，男装可以先算出2件上衣和2条裤子分别要多少元，再将其相加，算式是：60×2+40×2=200（元）;也可以把1件上衣和1条裤子搭配成1套，算出1套衣服的价钱，再算2套的价钱，算式是：（60+40）×2=200（元）。算女装的价钱与男装的方法是一样的，可以将上衣与裤子分开算，算式是50×3+30×3=240（元）;也可以将上衣与裤子搭配成1套算，算式是（50+30）×3=240（元）。

师：无论是算男装还是女装的总价，都可以用两种不同的方法解答，于是得出了下面这样两组等式：（60+40）×2=60×2+40×2，（50+30）×3=50×3+30×3。

在这个作业中，笔者创造性地将教材中求墙砖块数的情境问题，调整为购买男女生服装求总价的问题，以复习作业的形式呈现，这一问题更贴近学生的生活，可以充分激活学生的已有知识与生活经验，帮助他们结合生活体验，想到上衣、裤子分开算或者上衣、裤子搭配成套算这两种不同的方法，在解答实际问题的过程中初步感悟乘法分配律。

二、探究作业，整体构建

（一）探究乘法分配律

复习作业让学生对乘法分配律有了初步感悟，笔者思考的问题是：如何通过学习单将有逻辑意义的探究作业作为支架，帮助学生与作业对话，探究乘法分配律呢？

教师利用课件出示学习单中的独立探究作业一（如图1），问学生：观察左边的等式，你们能再写出几组这样相等的式子吗？（至少写3组），并试着用字母表示有这样特点的式子。完成后和同桌互相检查等式是否正确。

（学生独立完成后与同桌分享写法）

师：我们来分享几个同学写的等式，请你们在观察的同时用手势表示赞成还是反对。

（教师依次在实物投影仪上展示3个学生的学习单，其他学生口算后用手势表示对错）

师：从刚才分享的学习单中，同学们举例的等式都不一样，但这些算式的特点都相同。具有这样特点的算式写得完吗？你们现在能用最简单的数学语言表达这些算式的特点吗？思考后和同桌互相交流。

生：两个数的和乘一个数，可以把这两个数分别乘这个数，再把两个积相加。

生：两个数的和同一个数相乘，等于这两个加数分别乘这个数，所得的积相加。

师：你们的表达有所不同，但都简洁地表达了这些算式的特点。像这样，两个数的和乘一个数，可以把这两个数分别与这个数相乘，所得的两个积相加，结果不变，这个规律就叫乘法分配律。如果用a、b、c分别表示这3个数，你们会怎样用含有字母的式子表示乘法分配律？

生：（a+b）×c=a×c+b×c。

师：这样含有字母的式子就简洁地表达出了乘法分配律。

在独立探究作业中，笔者既呈现了复习作业中写出的两组等式，又提出了要学生再写3组等式及在此基础上用含有字母式子表示的要求，学生既要观察发现两组算式的特点，还要思考如何举例，在举例的过程中发现这样的等式写不完，于是就有了要用含有字母的式子去表达这一规律的需求，建立乘法分配律的模型。在表达规律时，学生既有数学语言的表达，又有含字母式子的表达，从而感悟到用字母式子表达规律的简洁性。

（二）解释乘法分配律

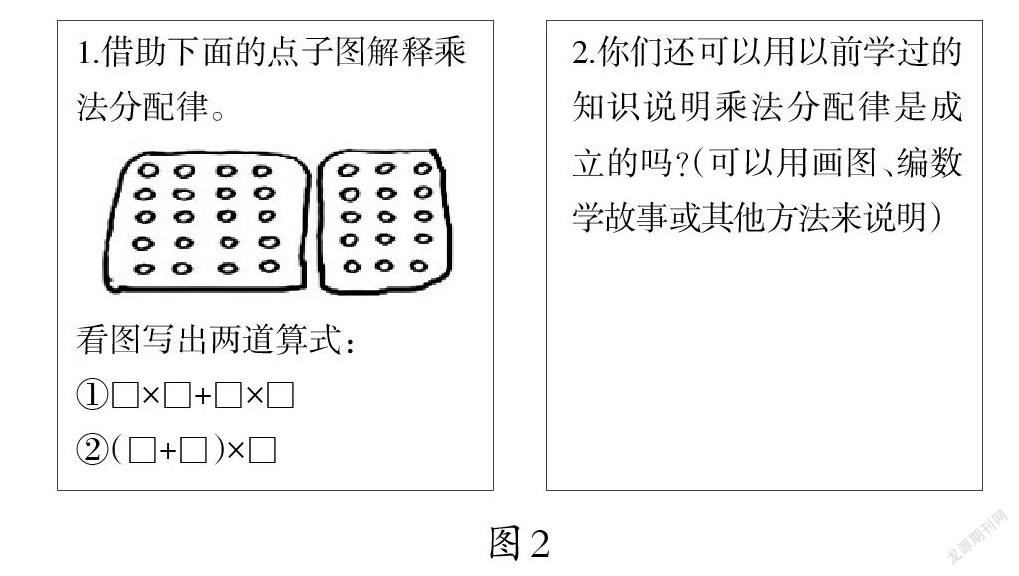
在建立了乘法分配律的模型后，笔者没有止步于此，而是思考如何通过作业提供学习材料，激活学生用已有经验去解释、应用规律，沟通新旧知识的联系的兴趣。于是笔者安排独立探究作业，有意识地给学生搭建了“借助二年级学习乘法时熟悉的点子图解释乘法分配律”支架，有了这个支架，学生再去理解乘法分配律就有了支撑，不同的学生会有不同的思考与方法。

师：同学们，乘法分配律是我们今天学习的新知识。学到这里，你们有没有发现，其实从二年级开始，我们就已经多次用过乘法分配律。

生：我想起来了，学习乘法时用到点子图。

师（课件出示学习单中的独立探究作业二）：如图2，这幅点子图就可以很好地解释乘法分配律。请你们看图完成算式，完成后思考还可以用以前学过的哪些知识来解释乘法分配律。

在学生独立完成探究作业后，他们会出现不同的解释方法。这个时候有两种反馈方案，一是让不同的学生分享想法;二是引导学生合作分享。笔者选择了方案二，因为方案二可以引导学生对比自己独立学习时想到的方法进行二次学习，从而完成新知识的整体建构。

师（课件呈现学习单中的合作分享作业）：我在巡视中发现，你们经过自己的努力想到了很多方法去解释乘法分配律是成立的。我把这些方法都整理到了合作分享作业中，请你们边看边思考：哪些方法是自己想到的？哪些不是？用最简单的数学语言和同桌说说赞成或反对的理由。

……

三、拓展作业，深度学习

师：同学们，学习到这里，我们探究了乘法分配律，并用以前学过的知识从不同的角度去解释了乘法分配律，为你们的努力点赞。学习就是要在有收获的同时，又产生了新的疑问，这才是真正的學习。此时，你们有了新的问题吗？（停顿等待）

生：我在想，学习了运算定律可以用它进行简便运算，那么乘法分配律是不是也可以让一些计算变得简便呢？

生：刚才学习的乘法分配律都是两个数的“和”乘一个数，如果是三个数或者更多个数的“和”乘一个数，还成立吗？

生：我又想到了新的问题，如果是两个数、三个数或者很多个数的“差”乘一个数，乘法分配律还成立吗？

师：因为我们一直在思考中学习，所以在学习中不断有新的问题要探究，真好。你们能想办法证明乘法分配律对几个数的“和”或“差”乘一个数是否成立吗？

教师课件出示学习单中的拓展与挑战作业：用举例的方法证明几个数的“和”或“差”乘一个数，乘法分配律是否成立。完成后和同桌分享学习成果。

在课堂教学中，教师要不断地促使学生提出新问题。当学生提出了有价值的问题时，教师要顺水推舟，以拓展作业的形式，放手让学生自发去验证。因为有了前面的学习基础，这一验证反而不难，绝大部分学生都在举例中很好地验证了乘法分配律对多个数的和或差与一个数相乘同样适用。这一作业始于学生的疑问，很好地引导学生的学习走向深入。

（作者单位：浙江省永康市解放小学）