动态连续时间网络表示学习

王 岩，任 浩，王 喆

吉林大学 计算机科学与技术学院，长春 130000

真实世界复杂系统实体之间的交互或者连接可以自然地表示为网络或者图，如互联网和万维网[1-3]、科学引用和合作系统[4-5]、传染病学[6-9]和通信系统[10]等。网络中的节点表示系统中的不同实体，连边代表实体之间的关系。网络结构有助于更直观地了解现实世界中实体之间的关系。例如，利用网络结构表示的社交网络数据，能够很清楚地表示社交网络中用户关注和被关注信息；在蛋白质相互作用网络里，连边展示了蛋白质间能否相互反应。对网络进行分析可以进一步了解网络的深层信息，例如链接预测、社区发现、节点分类等都得益于网络分析技术的发展。但是，由于网络可能包含数十亿个节点和连边，在整个网络上执行复杂的推理过程很难实现，并且网络结构数据不能直接作为机器学习算法的输入，所以如何对网络结构数据进行表示是一个重要问题。

传统的方法是在网络邻接矩阵的基础上进行分析研究。最直观的思路就是利用one-hot向量来表示网络的邻接矩阵，one-hot向量可以直接将网络中的每个节点编码成向量，并且向量维度与网络中节点的个数相同。这种方法虽然简单，但由于网络邻接矩阵高维稀疏，因而随着网络规模的增大，会耗费大量的时间和空间，并且one-hot向量不能准确表达出节点之间的相连关系。

随着表示学习技术在自然语言处理领域的不断应用，研究者开始将网络中的节点表示成低维稠密的向量。并且网络结构中相近的节点应具有相似的向量表示。向量表示的相似性一般用向量间的余弦或者欧氏距离表示。网络表示学习就是研究在尽可能保留原始网络结构信息的基础上，把网络结构数据转换为低维实值向量，并将其作为已有的机器学习算法的输入[11]。网络表示学习为揭示网络结构和执行各种网络挖掘任务提供了一种有效的方法。例如，节点的向量表示可以作为特征输入支持向量机（SVM）等分类器用于节点分类任务，同时，节点表示也可以转化成欧式空间中的点坐标，用于可视化任务[12-14]。网络表示学习不仅避免了传统方法的复杂计算，还提高了算法性能。

现有的大多数网络表示学习方法[15-17]通常关注静态网络结构，其中节点和边是固定的，不会随着时间而改变，并没有考虑网络的动态变化。但是现实世界大多是动态网络，其连边和节点都是随着时间不断变化的。这些时序信息是动态网络的重要部分，是网络演化机制的体现。例如，在社交媒体中，随着时间的推移，友谊关系的发展，电子邮件和短信等交流活动不断涌现。在推荐系统中，每天都会出现新产品、新用户和新评分。在计算金融中，交易是流动的，供应链关系是不断发展的。而静态网络表示学习方法不能根据时序信息更新节点表示，并且当网络发生变化时需要重新训练所有的节点表示。同时忽略时间信息可能会导致节点表示的不准确性。如图1所示，节点v1、v2、v3代表三个用户，假设从用户v1到用户v2有一封电子邮件ei=(v1,v2)，从用户v2到用户v3有一封电子邮件ej=(v2,v3)，同时T(v1,v2)为电子邮件ei=(v1,v2)的时间。因为T(v1,v2)=1＜T(v2,v3)=3，所以电子邮件ej=(v2,v3)可能反映了电子邮件ei=(v1,v2)的信息。但是T(v2,v3)=3＞T(v3,v1)=2，因此电子邮件ek=(v3,v1)不能包含电子邮件ej=(v2,v3)的信息。同时ek=(v3,v1)只能出现在ej=(v2,v3)前，如果不考虑连边产生的时间信息随机进行选择，很可能会导致结果出现偏差，这也说明了对实际序列进行建模的重要性。

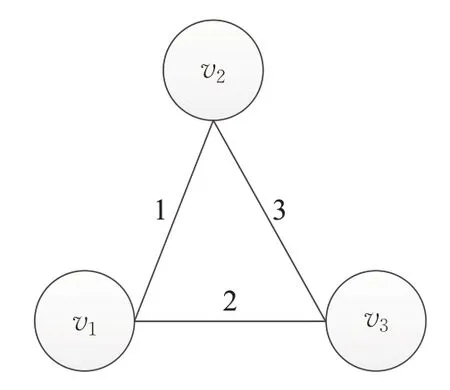
图1 电子邮件网络Fig.1 Email network

同时现有的动态网络表示学习方法[18-23]是将静态网络表示学习算法应用于动态网络中的每个快照，即记录相隔一定时间间隔的特定时刻的网络结构，并不能捕捉每个时间间隔内网络结构的具体演变过程，并且训练的时间复杂度会随着网络中顶点数量的增加而线性增加。

本文针对动态网络中节点之间建立连边的时间信息，学习适当的网络表示问题，以提高网络演化的预测准确性。通过描述了一个将时间信息合并到网络表示学习方法中的通用框架，能捕捉动态网络在连续时间上的演变特性，得到一个描述时序信息变化的网络表示。在随机游走过程中加入时间信息，尊重连边建立的先后顺序。同时考虑历史邻居的活动会影响当前节点的选择，建立模型考虑其影响变化。将采样得到的随机游走序列通过Skip-gram神经网络模型[24]训练得到节点的向量表示。本文使用网络分析任务——链接预测和节点分类来衡量网络表示学习算法的性能。

1 基于随机游走的动态连续时间网络表示学习模型

1.1 相关模型及定义

1.1.1 相关模型

（1）Word2vec[25]模型。Word2vec模型能够通过给定文本学习词向量表示，其基本思想是利用神经网络，通过训练，将文本中的单词转换到低维、稠密的实数向量空间中，通过向量空间中的向量运算来简化文本内容上的处理。例如文本的语义相似度可以通过向量空间上的相似度来衡量，可以用于自然语言处理中的很多工作，包括同义词寻找、词性分析等。

Word2vec包含CBOW和Skip-gram两种语言模型。这两种模型在借鉴自然语言处理模型的基础上进行了简化以便于计算，是包含了输入层（Input）、投影层（Projection）和输出层（Output）的三层神经网络。如图2所示。

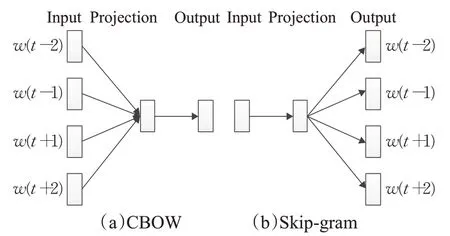
图2 CBOW模型和Skip-gram模型Fig.2 CBOW model and Skip-gram model

训练过程可以简述为：若给定某一语料库，使用一个固定长度为c的滑动窗口来遍历整个语料库，每次从整个语料库中抽取出一段语料进行训练。假设c=2，则每次的训练语料为wt-2、wt-1、wt+1、wt+2来预测词wt，训练过程如图2所示。输入层为wt的上下文wt-2、wt-1、wt+1、wt+2各个词向量，投影层是对输入层所有词向量进行累加求和，输出层通常采用层级Softmax或者负采样算法来表征已知上下文wt-2、wt-1、wt+1、wt+2的条件下wt出现的概率。Skip-gram模型的基本思想与CBOW相反，是使用某一词wt来预测上下文wt-2、wt-1、wt+1、wt+2，训练过程与CBOW模型类似。

（2）网络表示学习模型。网络表示学习是一种网络数据表示方法，将原始高维、稀疏的网络映射到低维稠密的空间中，并保留原始网络中的结构特性。通常关注节点向量化，即对于图G=(V,E)，学习一种映射f:Vi→Zi∈RD。其中Zi是一个将网络中节点映射后输出的表示向量，Zi的维度远远小于节点个数，即D＜＜|V|。图3表明了网络表示学习是所有基于复杂信息网络的分析任务的基础。

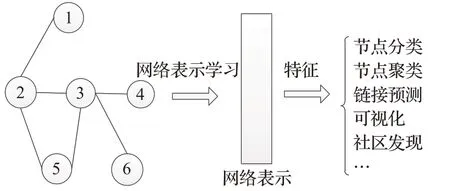
图3 网络表示学习过程示意图Fig.3 Network representation of learning process diagram

（3）基于随机游走的网络表示学习。Perozzi等人提出DeepWalk[15]算法第一次把深度学习领域的研究成果应用到网络表示学习中。首先证明了网络中节点随机游走的分布规律与自然语言处理问题中句子序列在其所用语料库中出现的规律服从类似的幂律分布。也就是说，如果在整个网络中的点遵循幂律分布，那么在某个随机游走的点上也遵循幂律分布。因此可以认为在网络上进行随机游走生成的序列的特性与NLP处理问题的对象很类似，从而将NLP中的词向量模型，用于网络节点中学习其向量表示。其整体思路是，在网络中进行长度一定的随机游走并且得到一系列等长度的随机游走序列，其中采样得到的每一个随机游走序列可以看作自然语言处理中的句子，通过Skip-gram模型中训练，得到节点的向量表示，并在网络分析上获得了很好的表示效果。由此得出，当对网络中的节点进行随机游走时，相比矩阵分解等方法，随机游走只需要依赖节点的局部信息而不需要将网络中所有节点的拓扑结构信息都存入内存，从而大大节省内存空间，并且可以有效降低邻接矩阵的方差和不确定性。同时随机游走可以记录网络的变化，即对网络中变化的节点和连边进行随机游走，而不需要重新计算网络中的所有节点表示。算法的整体框架如图4所示。

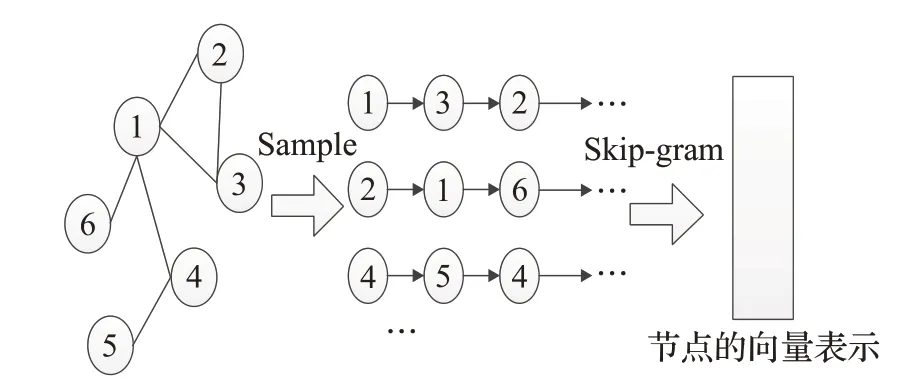
图4 基于Skip-gram的网络表示学习框架图Fig.4 Network representation learning framework based on Skip-gram

1.1.2 相关定义

定义1动态离散时序网络（dynamic discrete temporal network，DDTN）。在时序上对动态网络等间隔取快照，从而得到网络演化的离散序列，定义为DDTN={G1,G2,…,GT}其中Gt={Vt,Et}。如图5所示。这种表示方法相当于将动态网络拆解成单个静态网络序列，并不能捕捉所取间隔内网络的变化。

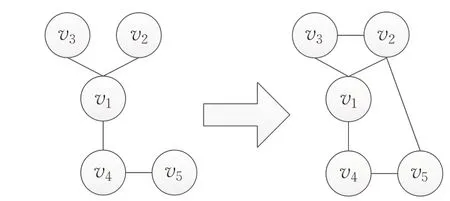
图5 网络演化过程中的两个快照Fig.5 Two snapshots of evolution of network

定义2动态连续时间网络（dynamic continuous temporal network，DCTN）。给定一个网络G=(V,ET,Φ)，V为节点集合，用ΕT⊆V*V*R+表示顶点关于时间信息的边的集合。用映射函数Φ:E→R+将边映射到时间戳上。例：图6中，Φ(v2,v5)=8。

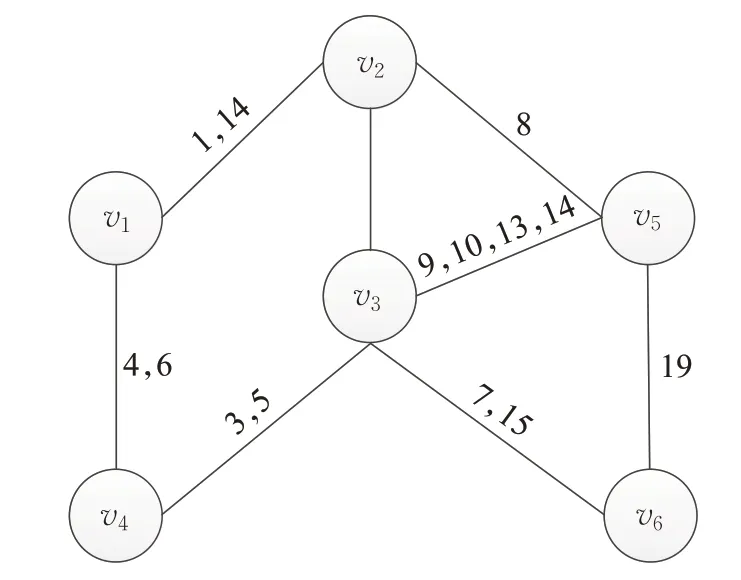
图6 动态连续时间网络Fig.6 Dynamic continuous temporal network

定义3时序邻居（temporal neighbor）。节点v在时间点t的时序邻居表示为Nt(v)，在传统网络的邻居节点集合的基础上，集合中的每个邻居节点w都对应一个时间戳t＇组成（节点，时间点）对。含义是节点v和邻居节点w在时间戳t＇连接。要求邻居节点所对应的时间戳t＇要大于此时时间点t。即：

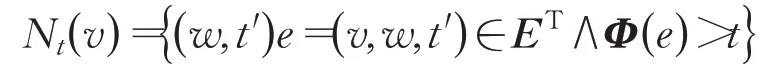
如图6所示，v3在t=3的时序邻居是{v2,v4,v5,v6}，在t=13的时序邻居是{v5,v6}。

定义4时序游走（temporal walk）。一个时序游走就是一个节点序列，要求其满足时间顺序：即节点是按照时间先后进行游走。也就是时序游走序列(v1,…,vi,vi+1,vi+2,…,vk)中Φ(vi,vi+1)≤Φ(vi+1,vi+2)如图6所示，当前时刻t=16时，v6到v3没有合法的游走序列，因为v6和v3建立连接的时间在t=16前；当前时刻t=13时，v3到v6有合法的序列，因为v3在t=13的时序邻居为{v5,v6}。

1.2 动态连续时间网络表示学习模型

1.2.1 问题定义

给定一个动态连续时间网络G=(V ,ET,Φ)，目标是学习一个函数f:V→RD，将节点映射到D维的空间中。D维的表示向量是基于时间信息得到的网络演化相关的网络表示，并且适用于下游的机器学习算法。

1.2.2 连续时间随机游走

给定源节点u，模拟长度为l的连续时间随机游走过程。ci为游走的第i个节点，起始节点c0=u。当前节点v在时间t时，c 服从以下分布：

其中，πvw是节点v和w之间的非正则化转移概率，Z是正则化常数。

1.2.3 采样策略

有偏随机游走是根据权重Wvw来选择下一个采样节点，即πvw=Wvw。考虑到不同历史邻居对当前节点选择下一个时序邻居节点的影响不同，且影响会随着时间的增长而逐渐衰弱，定义在t时刻，当前节点v和历史邻居节点h之间的权重：

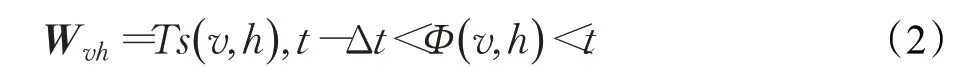
其中，Ts( v ,h)是在( t -Δt,t)时间内，节点v和历史邻居节点h建立连接的次数。因此在t时刻，当前节点v与时序邻居节点w之间的权重可以定义为：

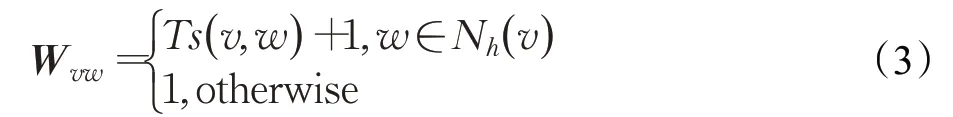
式中，Nh(v)是在( t -Δt,t)时间内，与节点v建立连接的历史邻居节点的集合。

1.2.4 时序窗口大小

由于时序游走会保留时间，遍历时可能会耗尽时间有效的边。因此，本文没有对采样的时序游走长度施加严格的限制，只需要每个时序游走最小长度为ω（ω相当于skip-gram的窗口大小），最大长度为L，以适应较长的游走序列长度。

1.3 学习DCTN节点嵌入

给定一个时序游走St，将学习节点嵌入的任务表示为最大似然优化问题，使用Skip-gram架构，需要优化的目标函数为：

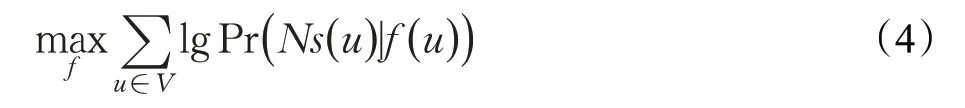
式中，Ns()u⊂V表示源节点u通过采样策略S所得到的网络节点序列。

算法流程如下：

算法1DCTNE算法

输入：G=(V ,ET,Φ)，向量维度D，每个节点生成节点序列的次数γ，生成节点序列最大长度L，窗口大小ω，时间间隔Δt。

输出：节点的向量表示矩阵H∈RD。

算法2时序有偏随机游走tiwalk

输入：G＇=(V ,ET,Φ,π)，起始节点u，序列长度L。

输出：节点采样序列walk。

2 实验结果与分析

2.1 数据集和参数设置

（1）emails数据集

该网络是利用欧洲一家大型研究机构的电子邮件数据生成的。边代表机构成员之间的电子邮件沟通。有向边( )

u,v,t是指机构成员u在t时刻发送电子邮件给成员v，该网络包含986位成员，时序边332 334条，根据成员所属部门的不同将所有成员进行分类。

（2）CollegeMsg数据集

该数据集是由加利福尼亚大学在线社交网络上发送的信息组成。用户可以在网络上搜索其他人，然后根据个人信息发送消息。边( )u,v,t指用户u在t时刻给用户v发送了一条消息。该数据集中有1 899个用户，时序边59835条，根据用户研究学科不同进行分类。

（3）friends数据集

该数据集是Facebook朋友关系图，其中节点是用户，用户之间的边代表朋友关系。该网络包含来自不同工作领域中的63 731个用户，时序边1 269 502条。

（4）DCTNE参数设置

节点的特征向量维度D=128，节点生成节点序列的次数γ=10，生成节点序列最大长度L=40，窗口大小ω=5。

2.2 基准算法

（1）DeepWalk

受到word2vec的启发，DeepWalk使用网络中节点与节点之间的共现关系来学习节点的向量表示。DeepWalk在网络中使用均匀随机游走得到若干序列，这些序列相当于自然语言中的句子，然后对序列中的节点对用层级softmax和Skip-gram模型进行概率建模，使序列似然概率最大，并且通过随机梯度下降来学习参数。实验中，使用默认参数设置：窗口大小ω=5，每个节点进行10次随机游走，随机游走的序列长度为40，节点的特征向量维度D=128。

（2）Node2vec

Node2vec由两个超参数p、q来控制随机游走的广度和深度，使其在深度和广度中达到一个平衡，能够保留节点局部和宏观的信息。实验中使用参数：p=0.25,q=4，节点的特征向量维度D=128。

（3）LINE

LINE是一种基于邻域相似假设的方法。该方法将学习到的D维特征表示为两部分：第一部分在直接邻居节点上模拟广度随机游走来学习D/2维的特征；第二部分从距离源节点2-hop的节点中采样学习剩下的D/2维特征，其中节点的特征向量维度D=128。

2.3 评价指标

通过构建混淆矩阵给出各评价指标的定义，如表1。其中，TP（True Positive），真正例，把正例预测为正类；FN（False Negative）假正例，把正例预测为负类；FP（False Positive）假正例，把负例预测为正类；TN（True Negative），真反例，把负例预测为负类。

表1 二分类混淆矩阵Table 1 Two-class confusion matrix

根据表1四种评价指标，得到更科学的评价指标：

（1）精确率（precision），又叫查准率，指的是预测值为1且实际值也为1的样本在预测值为1的所有样本中所占的比例：

（2）召回率（Recall），又叫查全率，指的是预测值为1且实际值也为1的样本在实际值为1的所有样本中所占的比例：

（3）准确率（Accuracy），预测正确的样本数占总样本数的比例：

（4）F1分数（F1-score），又称平衡F分数，是精确率和召回率的调和平均数：

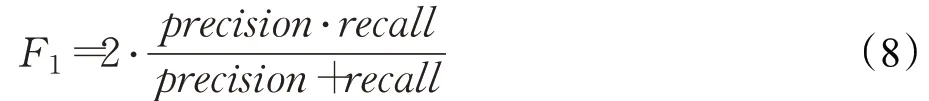
（5）Macro-F1和Micro-F1：针对多标签分类。

Macro-F1：计算出所有类别总的precision和recall，然后计算F1分数。

Micro-F1：计算出每一个类的precision和recall后计算F1分数，最后将F1分数平均。

（6）AUC（Area Under Curve）：被定义为ROC曲线下的面积。ROC曲线的横坐标为FP，纵坐标是TP，表示正例排在负例前面的概率。

2.4 实验效果与分析

2.4.1 链接预测

本文将链接预测作为二分类问题。在学习网络中节点向量表示V的基础上，通过Hadamard矩阵得到网络中边edge(u,v)的特征向量，即edge(u,v)=v⊗u，其中v⊗u=V*U，并预测在t时刻之后建立的边。将t时刻之后生成的边作为正样本，随机抽取t时刻之前的相同数量的边作为负样本。并且，在数据集上训练了一个逻辑回归分类器。链接预测的结果使用AUC值作为算法评价指标。实验结果如表2所示。

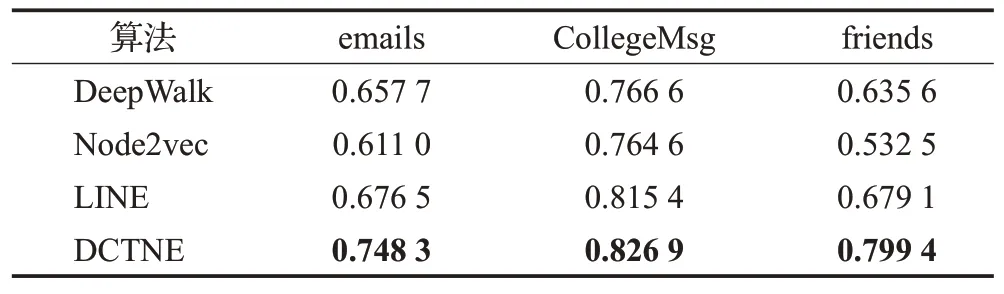
表2 链接预测的AUC值Table 2 AUC of link prediction results

在节点表示维度相同的条件下，将算法DeepWalk，Node2vec、LINE和DCTNE学习到的节点表示应用到链接预测任务效果中。实验中，DCTNE在emails数据集中的时间间隔Δt=2 000，在CollegeMsg数据集中的时间间隔Δt=2 000，在friends数据集中的时间间隔Δt=4 000。参数取值结果如图7所示。实验结果表明：DCTNE算法相较于算法DeepWalk、Node2vec、LINE将学习到的节点表示用于链接预测任务中效果较其他算法表现更好。在emails数据集上分别提高了13.7%、22.5%、10.6%，在CollegeMsg数据集上分别提高了7.86%、8.15%、1.41%，在friends数据集上分别提高了25.7%、50.1%、17.7%。DCTNE方法尊重了边缘形成的时间过程，将时间信息嵌入到节点表示中，从而在链接预测任务中优于其他算法。

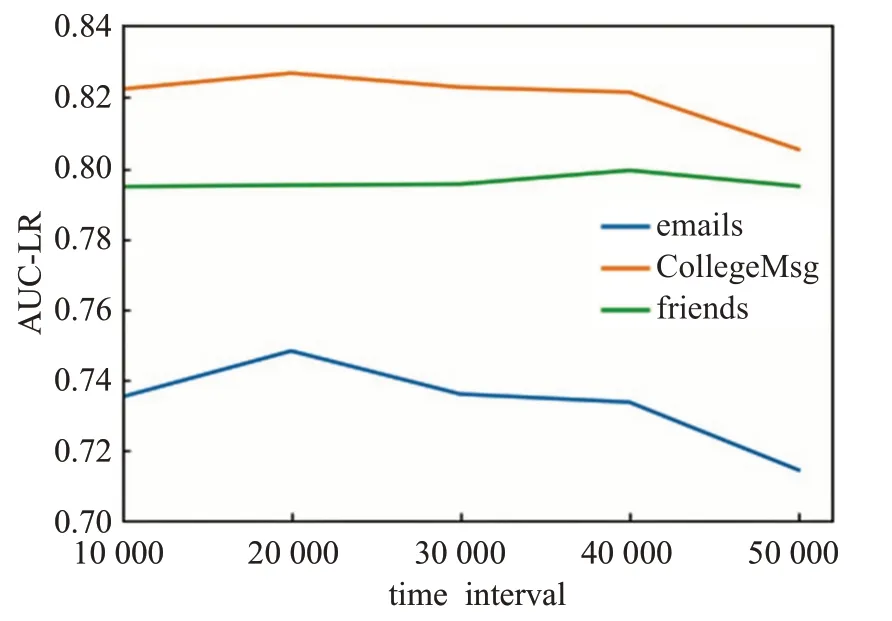
图7 不同Δt下链接预测的AUC值Fig.7 AUC of link prediction results under differentΔt

2.4.2 节点分类

节点分类是网络分析的重要组成部分，节点一般在网络中扮演着不同的角色。为验证DCTNE在节点分类任务上的有效性，在数据集emails、CollegeMsg和friends上执行多分类实验。对每个数据集分别使用DeepWalk、Node2vec、LINE、DCTNE学习表示向量，出于公平起见，上述方法均使用默认参数，表示向量维度为128。随机地将数据集划分为训练集和测试集，训练集比例为10%～90%，当训练集比例为10%时，测试集比例为90%，以此类推。使用XGBoost分类器对数据进行分类，并通过贝叶斯优化对分类器进行参数优化。由于这三个数据集的标签不是完全平衡的，使用Macro-F1分数作为性能度量，每个分类实验被重复10次得到平均分数，以减少分类器引入的噪声。实验中，DCTNE在emails数据集中的时间间隔Δt=3 000，在CollegeMsg数据集中的时间间隔Δt=2 000，在friends数据集中的时间间隔Δt=2 000。参数取值结果如图8所示。实验结果如表3～5所示。

表3 不同算法在emails数据集上的Macro-F1分数Table 3 Macro-F1 scores of different algorithms on emails dataset

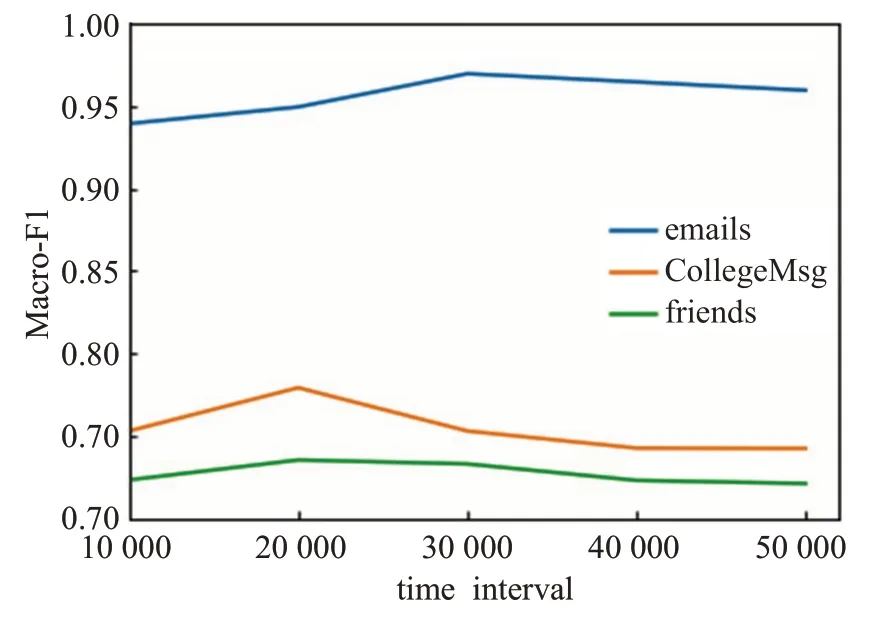
图8 不同Δt下Macro-F1分数Fig.8 Macro-F1 scores under differentΔt

从表中可以看出，DCTNE算法得到的节点向量表示的分类效果总体而言比DeepWalk、Node2vec、LINE算法得到的节点表示的分类效果好。实验结果证明，DCTNE算法学习到了网络的演化，有利于网络节点分类任务。

由于历史邻居会影响所捕获的邻居结构，且影响会随着时间t的增长而减弱。讨论时间间隔Δt在emails、CollegeMsg、friends三个数据集上的参数敏感性。实验结果如图7、8所示。从图中可以看出，DCTNE算法在三个数据集上的AUC值和Macro-F1分数在Δt的不同设置下结果不同，总体呈现先上升后下降的趋势。实验结果表明：当Δt取值较小时，游走序列会缺失部分信息，从而使实验结果准确率降低；当Δt取值较大时，游走序列会忽略近期历史邻居对当前邻居结构产生的较大影响，使得所有历史邻居对当前邻居结构的影响基本一致，忽略了由于时间而造成历史邻居对当前邻居结构的影响会随着时间增长而逐渐减弱的关系，从而使实验结果的准确率下降。

表4 不同算法在CollegeMsg数据集上的Macro-F1分数Table 4 Macro-F1 scores of different algorithms on CollegeMsg dataset

表5 不同算法在friends数据集上的Macro-F1分数Table 5 Macro-F1 scores of different algorithms on friends dataset

2.5 参数敏感性

3 结语

本文介绍了一种基于随机游走的动态连续时间网络表示学习算法，通过尊重边建立的时间信息来约束节点的随机游走序列。对于采样得到的节点序列通过Skip-gram模型得到网络的节点向量表示。实验结果证明：提出的算法DCTNE相比DeepWalk、Node2vec、LINE算法，能够考虑网络边缘建立连接的时间信息，从而很好地学习动态网络中的节点向量表示。同时适用于大规模网络数据集，且具有较强鲁棒性，即使在训练集比例较低时，仍优于其他对比算法。在未来的工作中，将进一步挖掘网络中节点之间的相互影响，结合节点标签信息和文本信息进行更准确的网络表示。