贯流式水轮机转轮叶片参数化设计与优化*

花 港,屈 波*,陈会向

(1.河海大学 能源与电气学院,江苏 南京 211100;2.河海大学 农业科学与工程学院,江苏 南京 211100)

0 引 言

转轮是将水流的水能转化为转动机械能的装置,转轮叶片的设计直接影响到水轮机组的整体效率和工作性能[1]。

传统的设计优化方法需要根据数值模拟计算的结果,进行反复修改和验证,耗费大量时间。随着计算机性能的提高和人工智能算法的发展,人们开始将智能优化算法应用于流体机械的优化设计。

罗兴锜等人[2]采用Bezier曲线对水轮机活动导叶叶片进行了参数化设计,用10个参数控制叶片前缘的形状,利用非支配排序遗传算法,减小了导叶的水力损失,提升了导叶表面的最低静压。朱国俊等人[3]采用Bezier曲线,对海流能水轮机叶片进行了参数化设计,用8个参数控制叶片压力面和吸力面的曲线形状,并运用径向基函数神经网络和非支配排序遗传算法,提高了翼型在不同工况下的升阻比性能。苗森春等人[4]采用B样条曲线,对单级离心泵叶片进行了参数化设计,用6个参数控制叶片型线,并使用遗传算法和反向传播(BP)神经网络,提高了离心泵在不同工况下的水力效率。王子瑞等人[5]采用Bezier曲线,对贯流式水轮机转轮叶片进行了参数化表达,用8个参数控制叶片骨线曲线,通过响应面分析和梯度寻优方法,提高了转轮叶片的效率。夏水晶等人[6]对轴流泵叶片进行了参数化设计,在叶片的5个不同截面分别选取进口角和出口角,用10个参数控制叶片形状,通过多岛遗传算法,提高了轴流泵的水力效率。JIANG B等人[7]采用Bezier曲线,对水泵水轮机转轮叶片进行了参数化表达,用5个参数控制叶片型线,通过粒子群优化方法,提高了水泵水轮机在最优工况下的效率和输出功率。

以上相关的研究结果说明,在水轮机叶片参数化设计方面,目前存在多种方法。同时,通过神经网络和遗传算法等方法对叶片的性能进行优化的手段也较为成熟,但其中仍然存在着参数化设计所需变量较多的问题,在优化的过程中难免会浪费大量的时间。

基于以上原因,笔者提出一种只需要4个变量的叶片参数化设计方法,通过改变叶片的部分位置的比例系数以控制叶片的形状,与之前的研究工作相比,在保证控制叶片形状的前提下,减少所需的参数数量,并通过BP神经网络和遗传算法,对某一贯流式水轮机转轮叶片进行优化设计,以期为水轮机叶片优化设计提供参考。

1 水轮机模型

笔者研究的贯流式水轮机的主要部分包括进水流道、前置导叶、转轮，以及后置导叶。

贯流式水轮机示意图如图1所示。

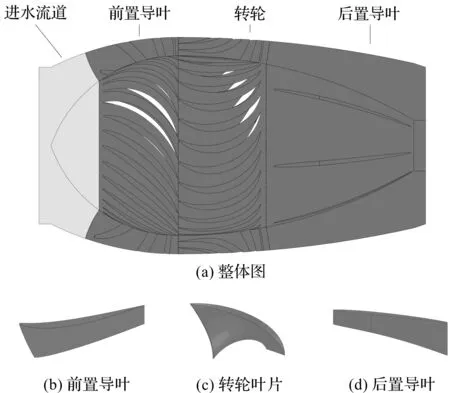
图1 贯流式水轮机示意图

该贯流式水轮机模型的主要参数有:

转轮直径D1为0.47 m,轮毂直径Dg为0.39 m;前置导叶叶片数为27,转轮叶片数为26;后置导叶叶片数为8;水轮机设计水头Hr为32.73 m,设计流量Qr为0.278 m3,设计工况转速n为750 r/min。

2 数值计算

2.1 控制方程

水流在贯流式水轮机的内部流动可以视为无热量交换的三维不可压缩黏性湍流,满足连续性方程和N-S方程[8-9]。

其中,连续性方程为:

▽·v=0

(1)

N-S方程为:

(2)

式中:p—流体压力;f—流体质量力;v—流体运动黏度;ρ—流体密度;v—流体流速。

此处,计算区域的模型建立与网格划分分别由SolidWorks和ICEM完成,并通过FLUENT对模型进行数值计算。其中,湍流模型采用k-ε模型[10,11]。

2.2 网格无关性验证

为保证数值计算结果的可靠性,笔者设置4种网格方案,计算时保持模型水轮机的进口压力和转速不变,并以模型水轮机在设计工况下的流量和效率作为网格无关性的验证标准。

网格划分方案如表1所示。

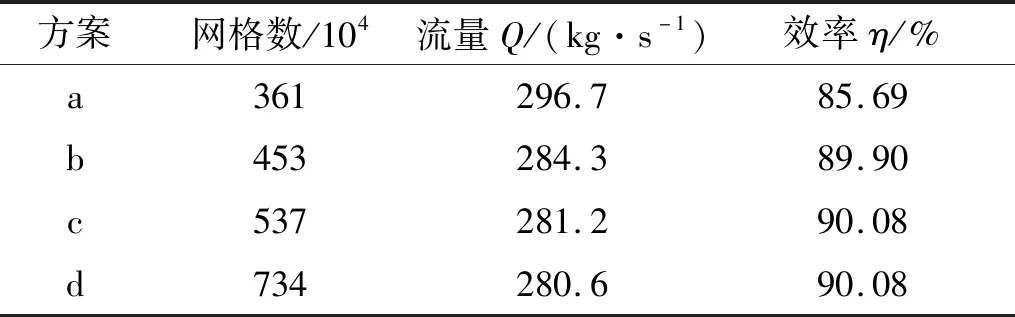
表1 网格划分方案

考虑到计算成本与准确性,笔者最终选取方案c为最终网格划分方案。计算域网格如图2所示。

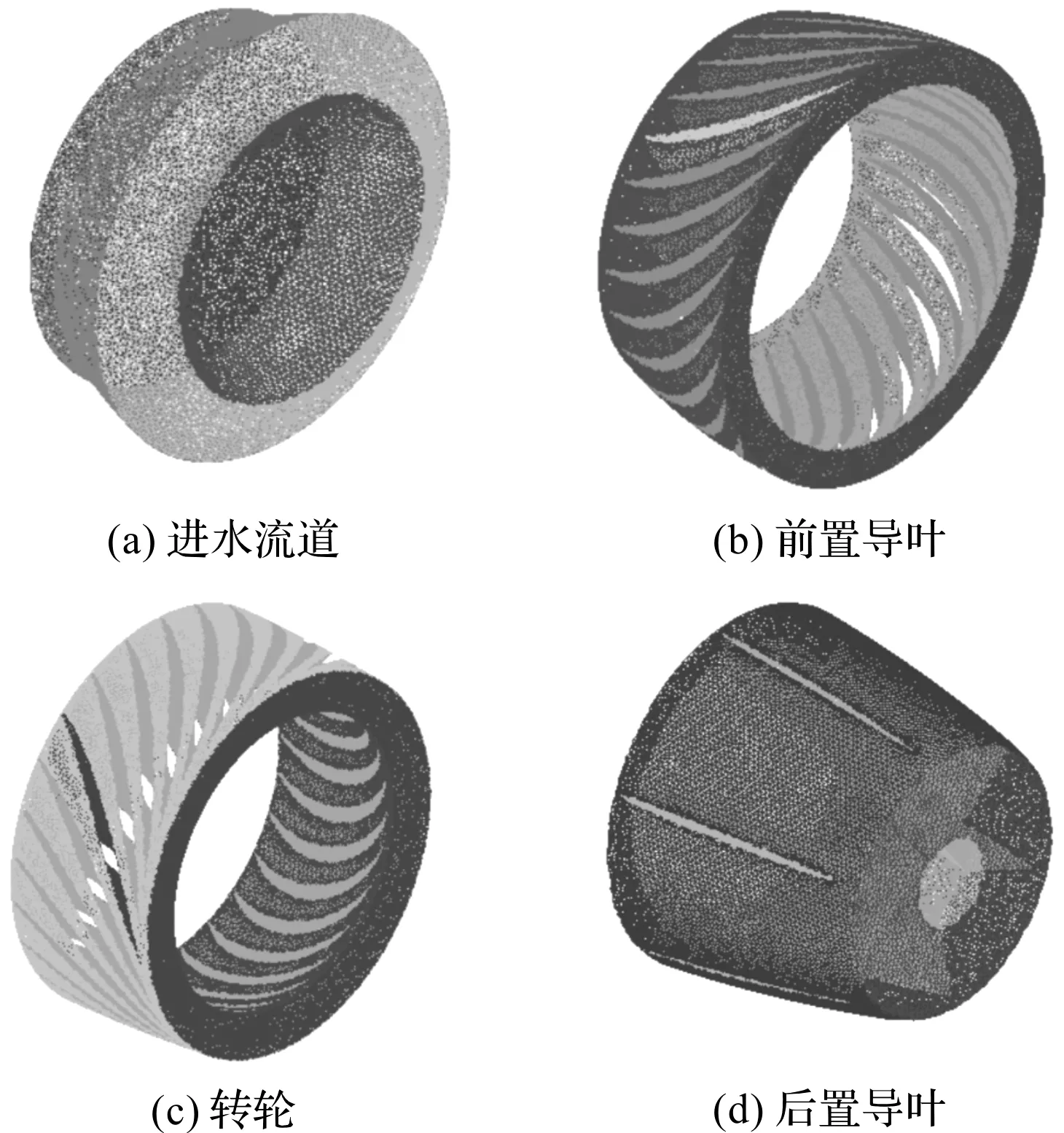
图2 计算域网格

2.3 边界条件

此处,水轮机的进出口边界分别设置为压力进口和压力出口,固壁面采用无滑移边界条件。

笔者将转轮区域设置为转动边界,壁面设置为无滑移边界条件,近壁区设置为标准壁面函数。为保证计算的收敛性,笔者将计算的监测残差设置为10-5。

3 叶片优化模型的建立

3.1 叶片的参数化造型

笔者在水轮机转轮的轮毂和轮缘间选取6个圆柱层截面,分别将其与转轮叶片曲面相交,得到6组转轮叶片翼型曲线。

转轮叶片三维结构示意图如图3所示。

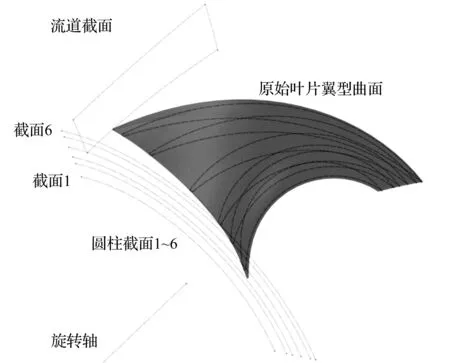
图3 转轮叶片三维结构示意图

笔者在保证各翼型曲线上的点P0位置保持不变的前提下,通过改变6个不同截面上的翼型,得到一个新的叶片翼型曲面。

二维翼型参数化示意图如图4所示。

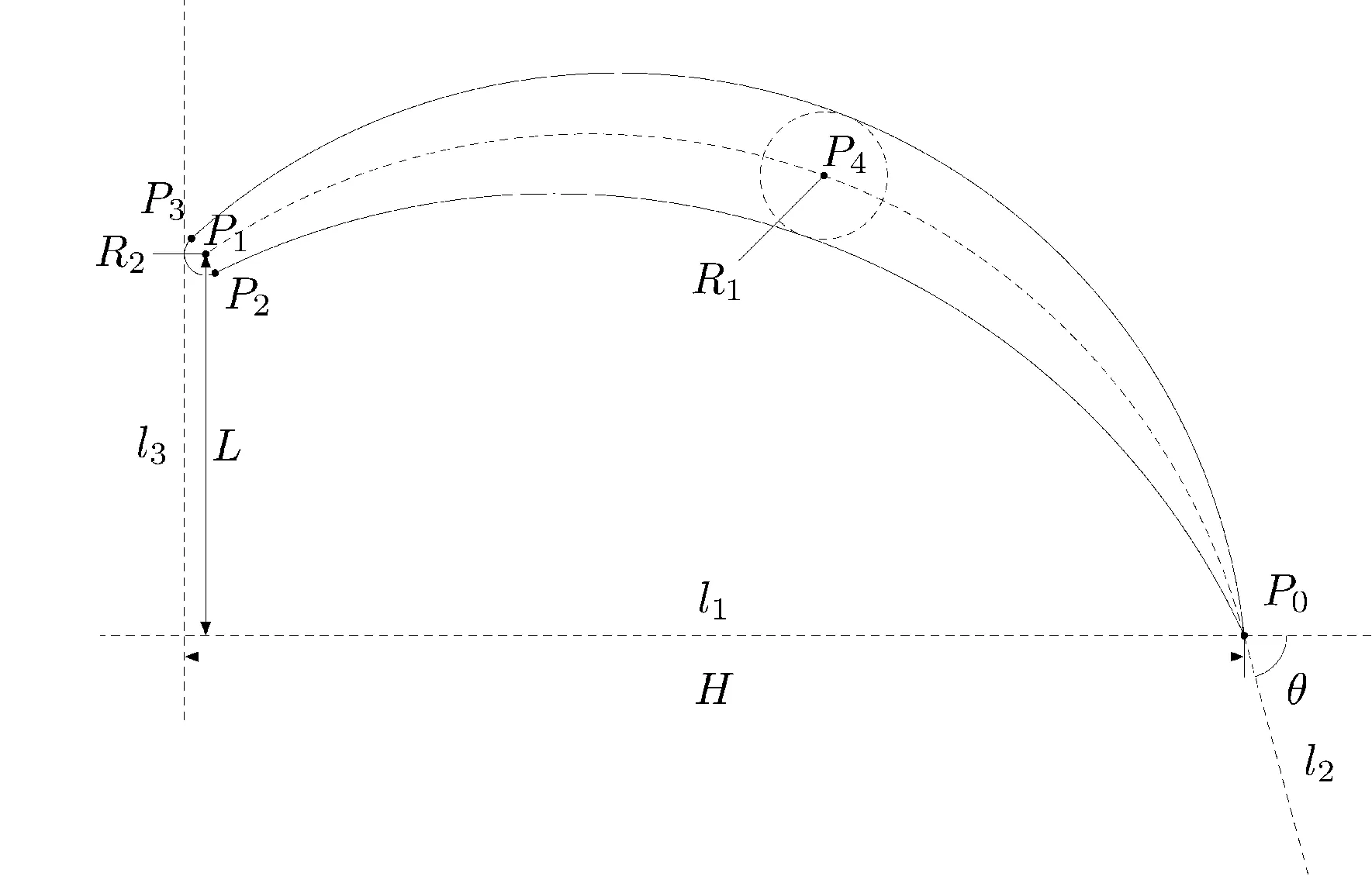
图4 二维翼型参数化示意图

笔者记新翼型在各截面上的参数为Xi,原始翼型在各截面上的参数为Xi0,其比值λX=Xi/Xi0。

此处,为减少变量个数,笔者令λHi=λR2i=1,i=1,2,…,6;记λR=λR1i,λθ=λθi。记λin=λL1=L1/L10,λout=λL6=L6/L60。

为保证叶片翼型曲面的连续性和光滑性,截面4的λL4需要满足下式:

(3)

笔者以截面到旋转轴的距离为x轴,Li值为y轴,由已知的3个点的数据,确定一条二次抛物曲线。其余各截面的Li值由二次抛物曲线的函数值决定。

轴面参数示意图如图5所示。

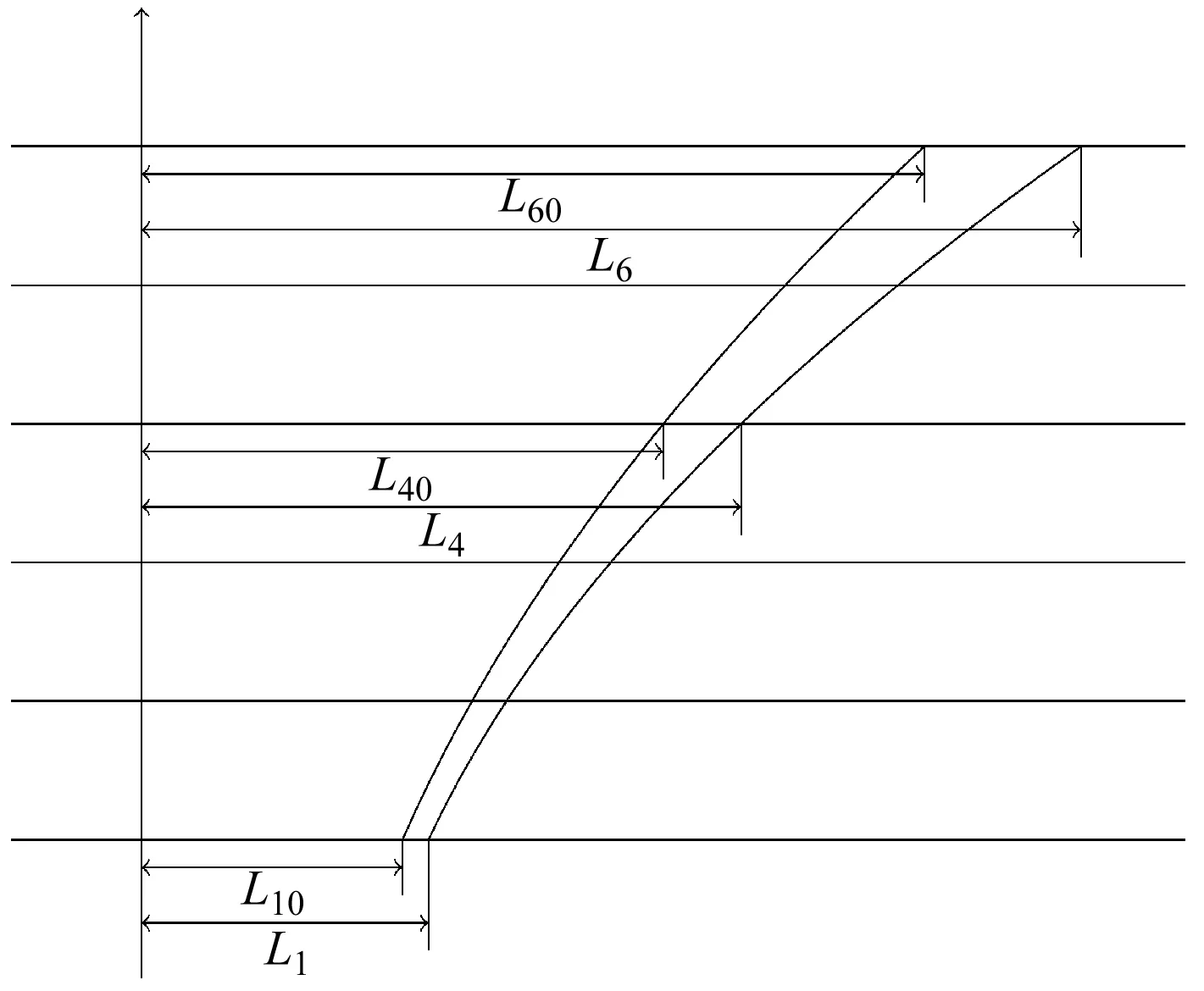
图5 轴面参数示意图

笔者采用上述原理,通过λR,λθ,λin,λout这4个变量,即可对叶片[12]翼型曲面进行控制。其中,λR代表叶片的厚度变化系数,λθ代表叶片后缘的出口角度变化系数,λin代表叶片轮毂的进口位置变化系数,λout代表叶片轮缘的进口位置变化系数。

与传统的水轮机叶片参数化设计过程中所需的变量个数相比,此处具有需要的变量个数较少。

设计变量的取值范围如表2所示。

表2 设计变量的取值范围

3.2 样本空间的建立

根据表2中各设计变量的取值范围,笔者建立神经网络训练样本空间,并采用SolidWorks进行几何建模,运用ICEM进行网格划分(网格划分采用表1中方案c的划分方法),通过FLUENT进行数值模拟计算,得到各样本点的水轮机效率。

试验设计与计算结果如表3所示。

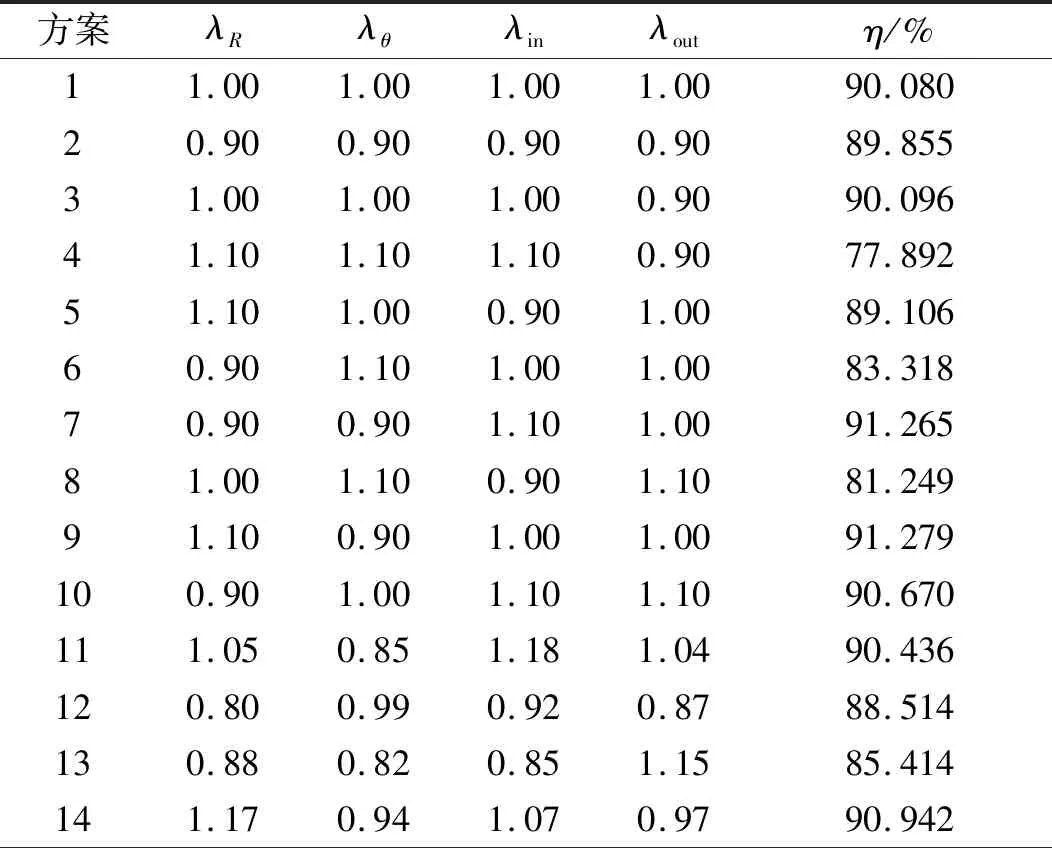
表3 试验设计与计算结果

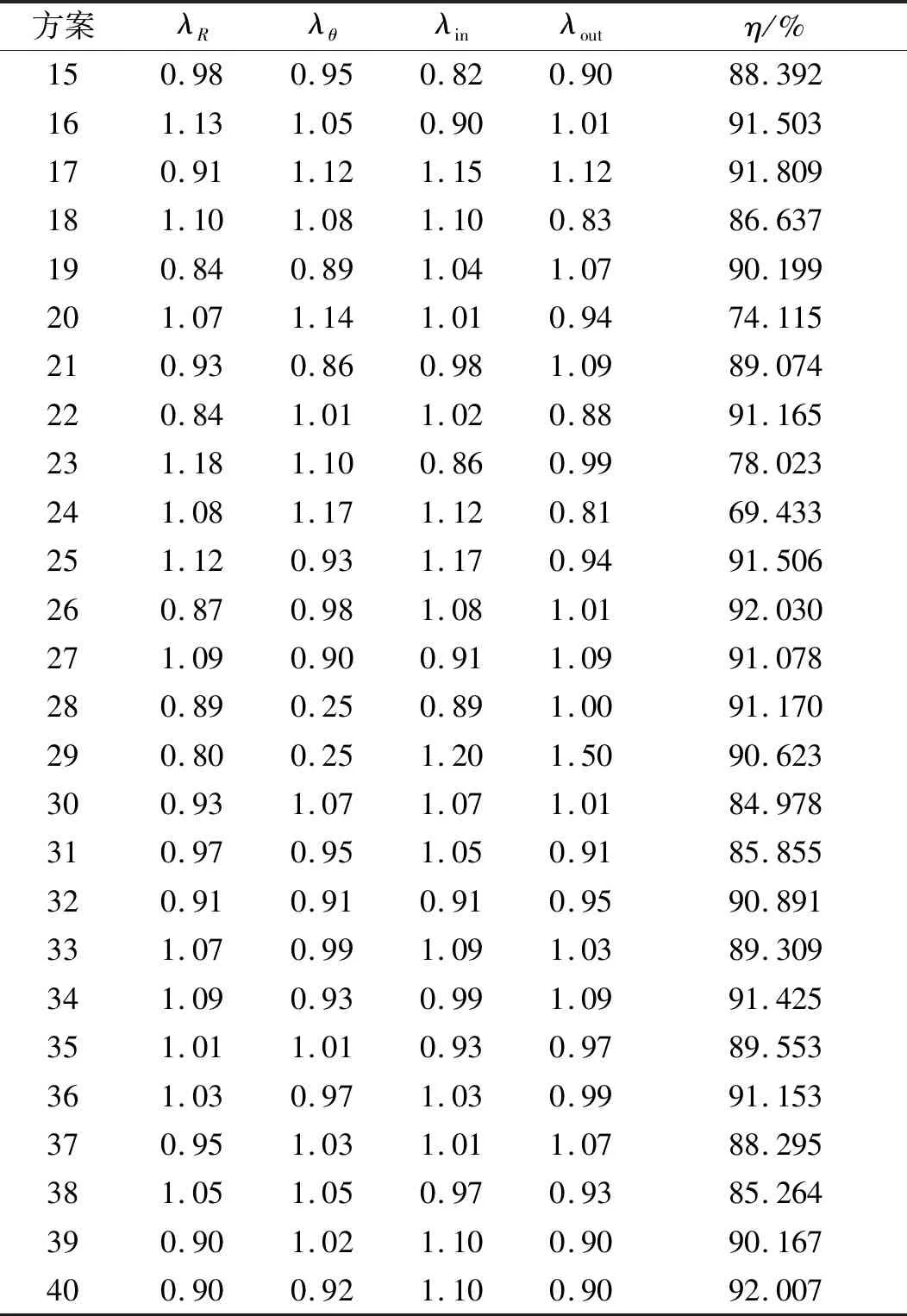
续表

3.3 预测模型的建立

BP神经网络[13,14]是应用最广泛的神经网络算法之一,其本质是根据误差反向传播算法训练的多层前馈网络。它具有较强的非线性映射能力和高度自学习、自适应的能力。笔者采用BP神经网络,建立对水轮机效率η的预测模型,并通过多次预测以减少误差。

在样本空间中,笔者选择80%的样本作为训练样本,20%的样本作为测试样本。

BP神经网络参数设置如下:训练循环次数为10 000,训练误差目标为0.000 001,学习效率为0.001。

测试样本的数值模拟值和预测值数据如表4所示。

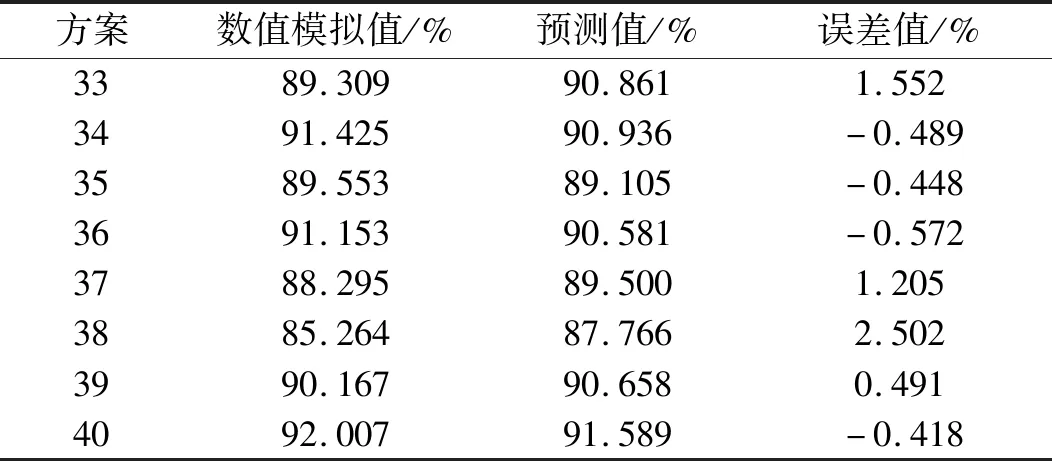
表4 测试样本的数值模拟值和预测值数据

此处的神经网络的复相关系数R2达到了0.95,可以认为满足工程要求,能够用该预测模型代替数值模拟进行计算。

3.4 遗传算法

遗传算法[15,16](GA)是一种具有自适应能力的、全局性的概率搜索算法,具有很强的鲁棒性和全局搜索能力。

此处笔者采用遗传算法,对水轮机的效率η进行优化。其中,优化中自变量分别为λR,λθ,λin,λout。

遗传算法参数设置如下:种群规模为40,进化代数为200,交叉概率为0.9,变异概率为0.01。优化过程中,遗传算法的适应度函数为水轮机效率,需要采用神经网络对其进行模拟。

优化结果对应的参数数据如表5所示。

表5 优化结果对应的参数

笔者根据优化得到的参数,做出优化后的水轮机[17]叶片翼型,并通过计算流体力学(CFD)数值模拟计算进行验证,得到实际水轮机效率为92.62%,优于样本空间的最优效率值。该结果证明了该优化算法的有效性。

优化前后,不同截面上的翼型曲线对比结果如图6所示。

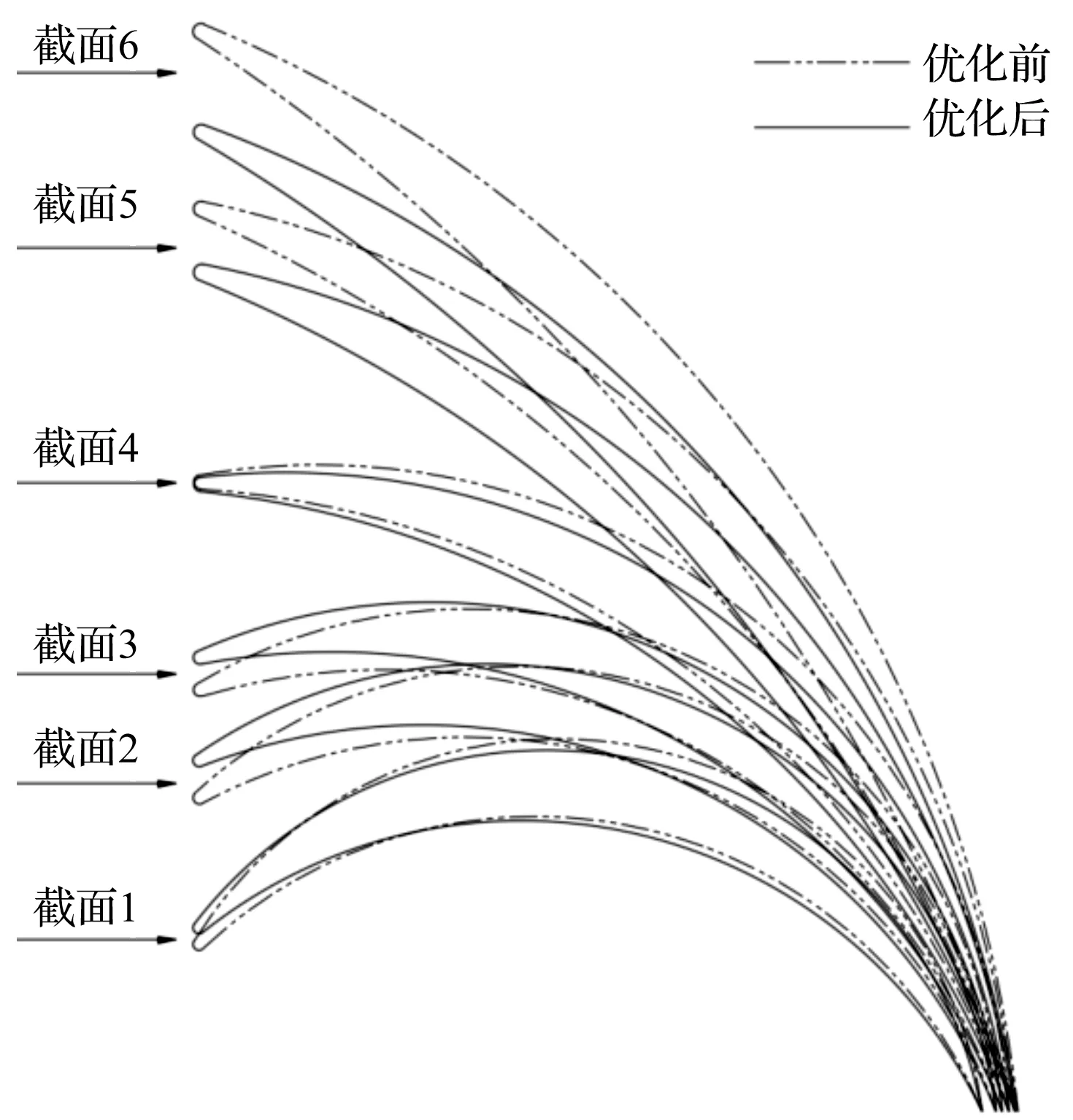
图6 优化前后不同截面上的翼型曲线对比

优化前后叶片形状的对比结果如图7所示。

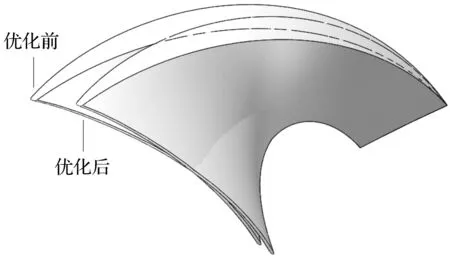
图7 优化前后叶片形状对比

优化前后叶片参数的结果对比如表6所示。

表6 优化前后叶片参数对比

4 优化结果分析

对比优化前后叶片的几何形状可知:优化以后,叶片的厚度和叶片后缘的出口角度有所减小,叶片在空间的扭曲程度也有所变化。这说明通过神经网络和遗传算法进行优化计算后,原先的叶片已经被优化,可以得到水力效率更高、水力性能更优的叶片。

为了分析优化前后叶片翼型曲线形状对水轮机转轮内部流场性能的影响,笔者选取了优化前后叶片上的2个截面的压力分布进行比较。

2个截面按转轮轮毂到轮缘的叶高方向定位分别为10%和90%。在叶片靠近轮毂的位置(10%叶高处),优化后叶片前缘处的最大压力小幅降低,叶片后缘处的最小压力小幅提高,压力面与吸力面的压差有较大的提高;在叶片靠近轮缘的位置(90%叶高处),优化后叶片前缘处的最大压力大幅降低,叶片后缘处的最小压力小幅提高,压力面与吸力面的压差增大。

优化前后叶片截面压力分布图如图8所示。

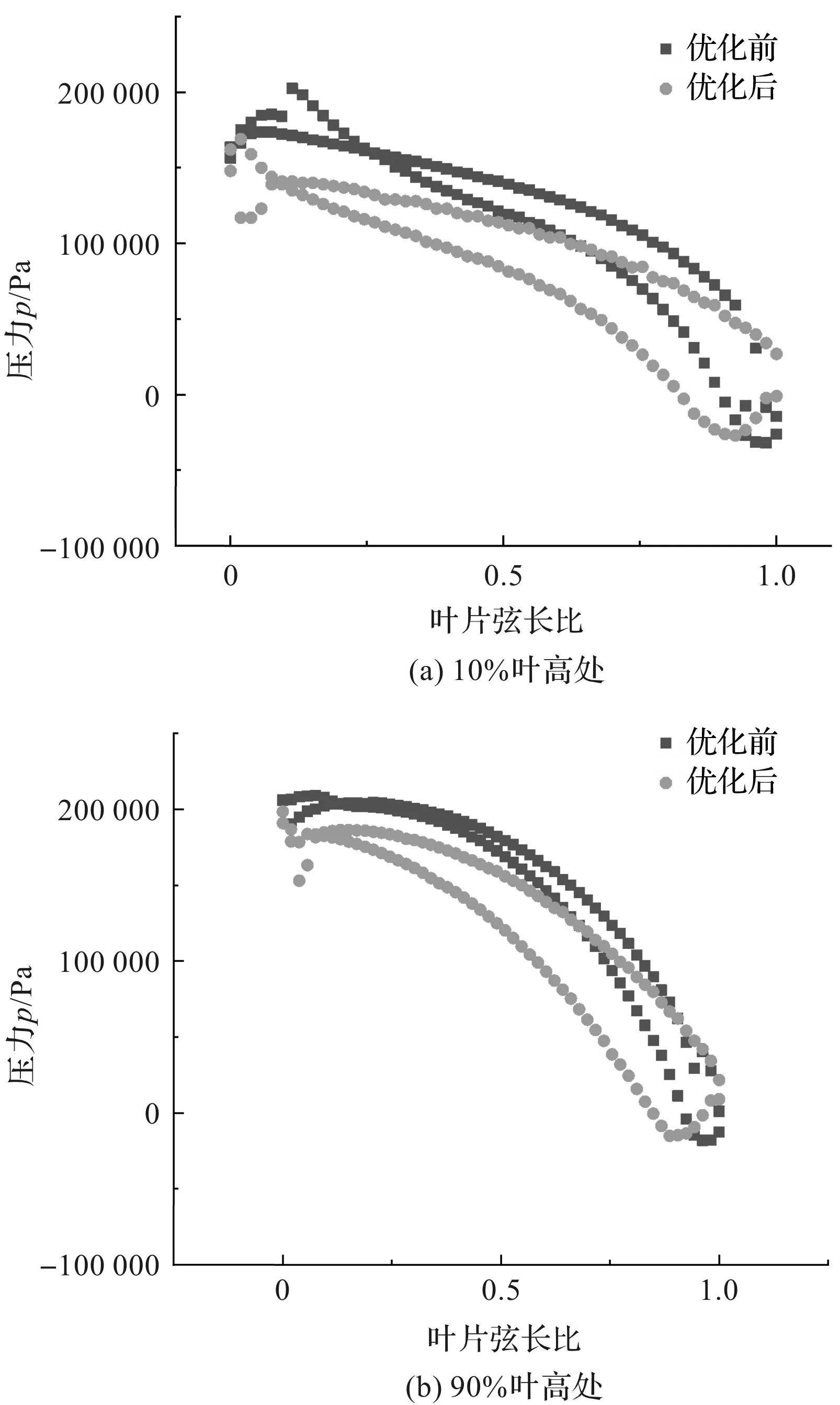
图8 优化前后叶片截面压力分布图

在优化前后,叶片压力面与吸力面的静压分布规律有一定的相似性,并且优化后的叶片的压力变化更加平滑。这表明优化后叶片的压力分布得到了有效的提升,在减小了叶片载荷的同时,提高了叶片的做功能力和气蚀性能,有利于机组的安全稳定运行。

优化前后叶片表面静压力云图如图9所示。

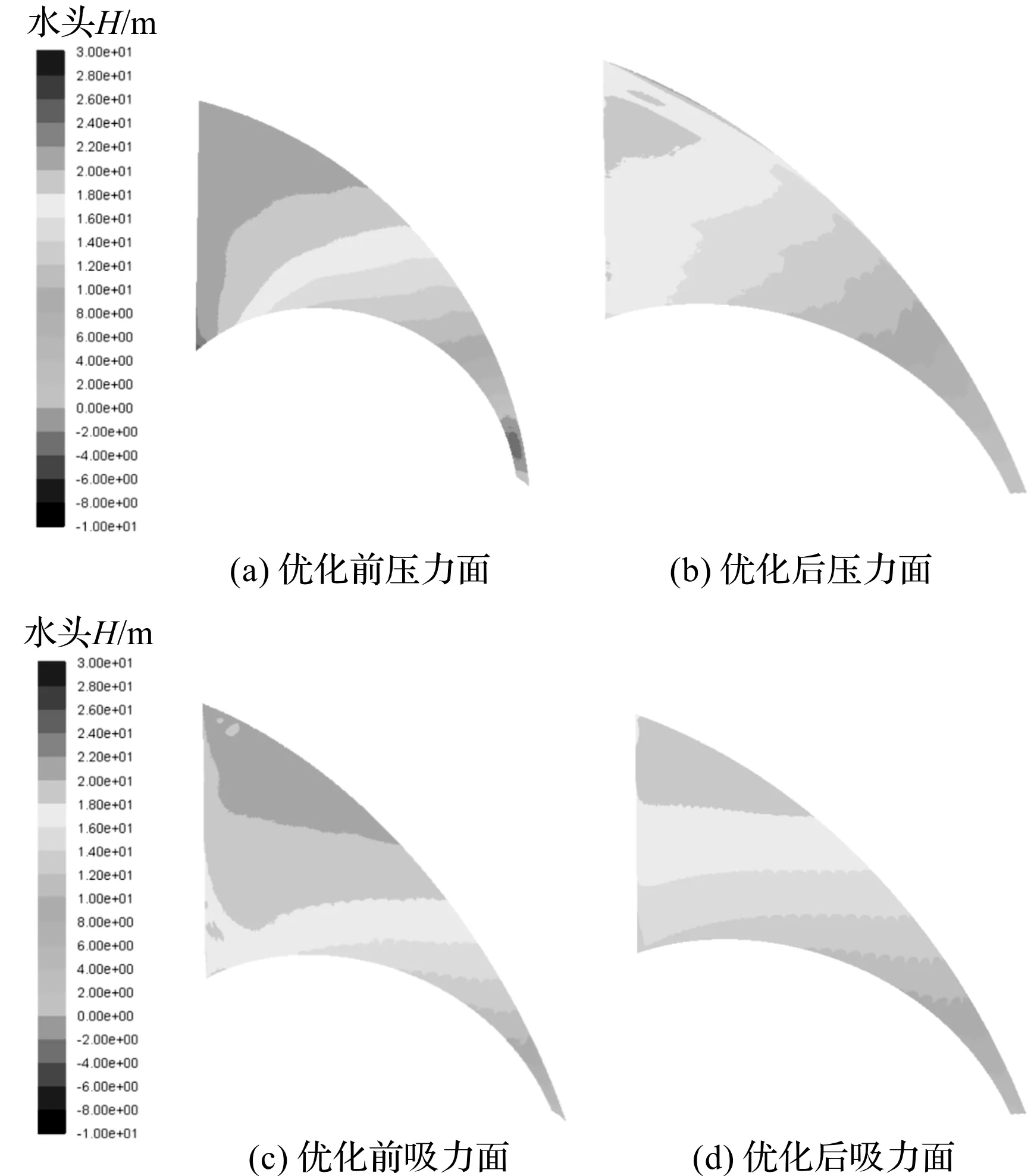
图9 优化前后叶片表面静压力云图

为了研究优化前后叶片在不同工况下的水力性能,笔者计算了优化前后水轮机在不同流量下的工作情况。计算结果表明,与优化前的叶片相比,优化后的叶片在1.0Qr、1.1Qr、1.2Qr这3个工况点具有较高的水力效率,而在0.8Qr、0.9Qr这2个工况点效率明显降低。

该结果说明,为了保持水轮机的高效运行,需要保持实际流量Q不低于设计流量Qr。

优化前后水轮机的性能曲线如图10所示。

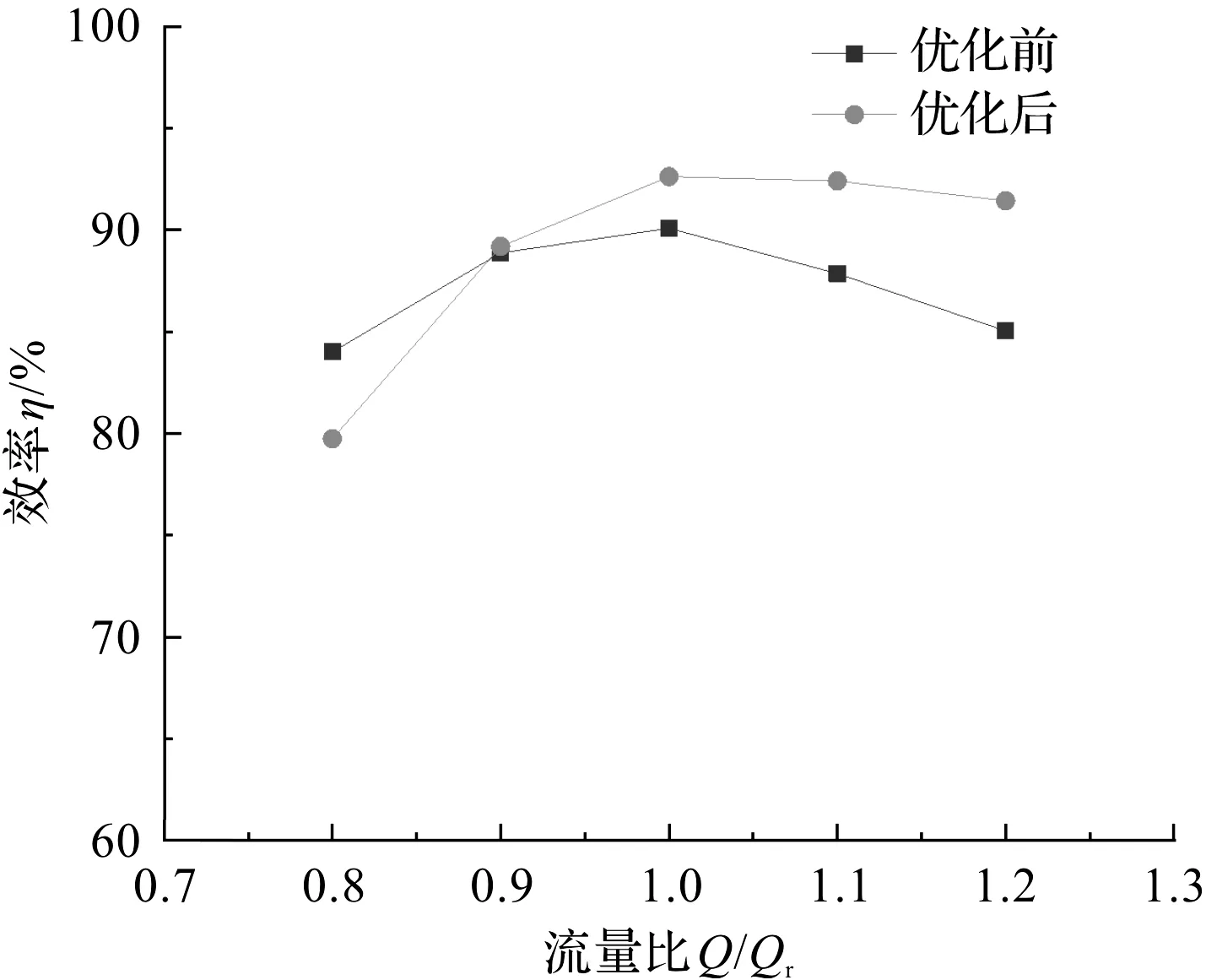
图10 优化前后水轮机性能曲线

5 结束语

在水轮机优化设计过程中,水轮机叶片所需变量多,且优化过程计算量大,为此,笔者提出了一种水轮机转轮叶片优化设计方法。

笔者首先对水轮机叶片翼型曲线进行了参数化设计,采用CFD得到了不同参数、相同工况下叶片的计算结果,并生成样本空间;结合BP神经网络和遗传算法,对水轮机的效率和水力性能进行了优化计算;最后对得到的优化结果进行了CFD数值模拟计算,并将其与原型叶片进行了对比分析。

研究结果表明:

(1)笔者使用二次曲线对叶片进行了参数化设计,通过改变叶片部分位置的比例系数,控制水轮机叶片的形状;其与传统的水轮机叶片参数化设计相比,减少了需要的参数个数,也减少了后续优化计算过程的运算量;

(2)在设计工况下,优化后的贯流式水轮机的水力效率提高了2.5%,叶片的压力分布情况得到了有效的提升,叶片的做功能力得到了提高,气蚀性能得到了改善;

(3)在流量略高于设计流量时,优化后的贯流式水轮机能够达到较高的水力效率。

在后续的研究中,笔者将进一步研究如何改善模型水轮机在低于设计流量的工况下效率迅速降低这一问题。