基于IWOA-LSSVM的联合收割机装配质量检测研究*

马毅臻,赵思夏,徐立友,陈小亮

(河南科技大学 车辆与交通工程学院,河南 洛阳 471003)

0 引 言

联合收割机是一种可以一次性完成作物收割、输送、脱粒、分离清选的大型农用复杂机械[1,2],其工作过程中的可靠性直接关系着农作物收获作业的质量和效率[3]。

由于收割机传动系统复杂,传动系统的装配故障会导致联合收割机工作过程中零部件磨损加剧,严重减少无故障工作时间[4]。因此,有必要对联合收割机的装配故障检测方法进行研究,以提高其工作的可靠性。

目前,针对旋转机械系统的故障诊断研究很多,其中的大部分研究都是采用智能算法构建起故障的诊断系统,然后再对机械系统的振动信号进行分析。作为一种多方法融合的模式识别过程,故障诊断通常包括4个步骤,即振动信号采集、信号预处理、故障信号特征提取、构建分类器[5]。其中,构建分类器是完成故障诊断工作的最后一环;同时,分类器的性能优劣会直接影响整个诊断过程的效果。

作为一种经典的监督学习方法,支持向量机(SVM)于1960年被推出,之后SVM得到了大量应用,常用于故障诊断系统分类器的构建[6,7]。

李运等人[8]提出了一种基于SVM的新异类故障检测方法,实现了对望远镜驱动系统的性能检测。周建民等人[9]通过构建优化后的SVM分类器,实现了对滚动轴承退化状态的识别。SUYKENS J A K等人[10]将最小二乘线性理论引入传统SVM中,将原始的SVM不等式约束转化为线性等式约束,并提出了最小二乘支持向量机(LSSVM),使其求解过程更加高效、简洁,提升了计算的速度和精度。

但是LSSVM的分类效果极易受到模型中各参数的影响,因此,一些学者采用遗传算法(genetic algorithm,GA)和粒子群算法(particle swarm optimization,PSO)优化LSSVM参数[11,12]。

但是,这些算法仍然存在局部能力弱、全局搜索能力一般、易早熟等缺点。

鲸鱼优化算法(WOA)[13]是2016年由澳大利亚学者MIRJALILI S提出的一种新的群智能算法。标准的WOA算法具有参数少、全局收敛性好等优点。

董东林等人[14]使用WOA来优化ELM,实现了对矿井突水水源的快速判别。谢丽蓉等人[15]利用WOA对LSSVM进行了优化,建立了超短期风电功率预测模型。

虽然WOA具有参数少、操作简单、寻优能力强等优点,但仍存在收敛精度低、容易陷入局部最优解等问题[16,17]。基于此,国内外一些学者对WOA进行了改进研究。

汤安迪等人[18]通过引入立方映射混沌算子改善鲸鱼种群,对无人机的航机规划问题进行了优化。刘浩然等人[19]提出了一种基于交叉变异算子和动态参数调整策略的WOA算法。郑威迪等人[20]用莱维飞行方法代替了原始WOA的参数随机选择方法,加快了WOA算法的收敛速度。孔芝等人[21]提出了一种基于自适应调整权重和搜索策略的鲸鱼优化算法,解决了算法的早熟问题。

虽然WOA已经广泛应用于多个领域,但在处理更加复杂的优化问题时,仍然存在寻优速度慢和易陷入局部最优解等问题。同时,一些学者在改进算法时,在算法的种群位置更新初期增加了权重因子,以增加种群的多样性,但这会造成收缩包围后期种群的更新变化速度变缓,使其无法很好地平衡局部搜索和全局搜索的能力。

针对上述问题中存在的不足,笔者在WOA基础上引入余弦控制因子和正弦时变自适应权重。在算法迭代初期,种群较为分散,余弦控制因子变化较慢有利于算法的全局搜索;在迭代后期,余弦控制因子变化速度增加,算法的局部搜索能力增强。而且,笔者仅在螺旋位置更新时加入正弦时变自适应权重,增强了算法全局搜索和跳出局部最优的能力。

笔者首先使用8个基准测试函数对改进的鲸鱼优化算法(IWOA)进行测试,然后采用IWOA对LSSVM进行优化,并将其与互补集合经验模态分解(CEEMD)[22]相结合,构建起联合收割机零部件装配质量检测模型,并将其在东方红4LZ-9A2联合收割机上进行试验,以验证检测模型的有效性。

1 鲸鱼优化算法

鲸鱼优化算法是一种通过模拟座头鲸气泡网捕猎行为的元启发式优化算法。其狩猎过程主要包括3个阶段:包围猎物、气泡攻击和搜寻猎物。

(1)包围猎物。座头鲸可以识别猎物,并且对其进行包围。

假设当前最佳种群个体的位置为目标猎物位置,或者最接近最佳的目标猎物位置,其余个体会朝着目标位置前进,并更新自身的位置,其位置更新公式为:

X(t+1)=X*(t)-A·D

(1)

D=|C·X*(t)-X(t)|

(2)

式中:A,C—系数向量;X*(t)—种群中最优个体所处位置;D—最优个体与当前个体位置X(t)之间的距离。

向量A与C的表达式分别为:

A=2a×r1-a

(3)

C=2·r2

(4)

(5)

式中:tmax—最大迭代次数;r1,r2—取值范围在[0,1]中的随机向量。

其中:a的值随t的增加从2线性下降到0。

(2)气泡攻击。捕食模型包括两部分:

第一部分是收缩包围,A的值随控制参数a而变化,为局部搜索阶段;

第二部分是螺旋位置更新,鲸鱼根据自身与目标之间的距离,以螺旋运动实现包围,其数学模型可表示为:

D′=|X*·(t)-X(t)|

(6)

X′(t+1)=D′·ebl·cos(2πl)+X*(t)

(7)

式中:D′—第i只鲸鱼到目标的距离;l—[-1,1]之间随机变换生成的参数;b—螺旋常数。

鲸鱼在攻击猎物时,收缩包围和螺旋位置更新同时进行,具有相同的发生概率。其具体数学模型为:

(8)

式中:p—[0,1]之间的随机数。

(3)搜索阶段。鲸鱼在攻击猎物时,会随机搜索猎物。

当|A|>1时,随机选取个体位置进行全局搜索以免进入局部最优解,其表达式为:

D=|C·Xrand-X(t)|

(9)

X(t+1)=Xrand-A·D

(10)

式中:Xrand—随机选择的鲸鱼个体位置向量;X(t)—当前个体的位置向量。

2 鲸鱼优化算法的改进

2.1 余弦控制因子

鲸鱼优化算法具有原理简单易懂、超参数少等优点,但在寻优过程中也需要平衡局部搜索和全局寻优的能力,即通过改变A的值进行调整。

由式(3)可知,A的值由参数a进行控制,a值越大,算法全局搜索能力越强;a值越小,算法局部搜索能力越强。

在标准的鲸鱼优化算法中,a的值为从2线性下降到0的参数。其在运行过程中容易陷入局部最优解,因此笔者在此处使用非线性控制因子,其表达式为:

(11)

从式(11)可以看出:在算法迭代前期,a值较大,且从2开始缓慢减小,以充分进行全局搜索;在算法迭代后期,a值减小，速度增加,局部搜索能力增强。

2.2 正弦时变自适应权重因子

文献[23]指出,权重因子较大时有利于算法的全局搜索,而权重因子较小时有利于算法的局部搜索,因此,为了有效平衡算法的局部搜索和全局搜索能力,笔者在算法更新位置时引入自适应权重因子,以此来提高算法的收敛速度和精度。

更改后的数学模型为:

(12)

其中,权重w(t)表达式为:

(13)

2.3 改进算法复杂度分析

时间复杂度体现了算法的运行效率,是评判算法性能优劣的重要因素[24]。在改进的鲸鱼优化算法中,鲸鱼算法的种群规模为N,个体的设置维度为n。

笔者设置最优个体初始位置与适应度初值的时间为t1,初始化鲸鱼个体位置每一维的时间为t2,则初始化阶段的时间复杂度为:

T1=O(t1+N(n·t2))

(14)

开始迭代以后,总的迭代次数为M。假设种群中每只鲸鱼计算目标函数适应度值的时间为f(n),与当前最有适应度值比较替换的时间为t3,系数向量A和C的计算时间为t4,则该阶段的时间复杂度为:

T2=O(N(f(n)+t3+t4))

(15)

假设种群中有m1只鲸鱼进行寻走觅食,位置更新时间为t5;m2只鲸鱼对猎物进行收缩包围,位置更新时间为t6;m3只鲸鱼进行螺旋位置更新,执行时间为t7;在进行位置更新时,引入的正弦时变自适应权重w(t),增加了t8的计算时间,头鲸螺旋游走攻击猎物N=m1+m2+m3,0≤m1,m2,m3≤N,则该阶段的时间复杂度为:

T3=O(N(m1(n·t5)+m2(n·t7)+
m3(n·(t7+t8))))

(16)

综上所述,IWOA的总的时间复杂度为:

T=T1+M(T2+T3)

(17)

此外,空间复杂度S(n)主要受种群规模和搜索空间维度的影响,可以表示为:

S(n)=O(f(n))=O(N×n)

(18)

2.4 算法性能测试

为了验证IWOA算法的性能,笔者采用8个基准测试函数进行测试,并将其与WOA算法进行比较,将两种算法所求的最优值均值和标准差作为评价指标。

笔者设置种群数为30,最大迭代次数为100,维度为30。

基准测试函数如表1所示。

表1中,F1～F4为连续单模态函数,F5～F8为非线性多模态函数。

表1 基准测试函数

考虑到实验结果的有效性和准确性,笔者将两种算法分别在8个基准测试函数上独立运行30次。

寻优计算的均值、标准差和运行时间如表2所示。

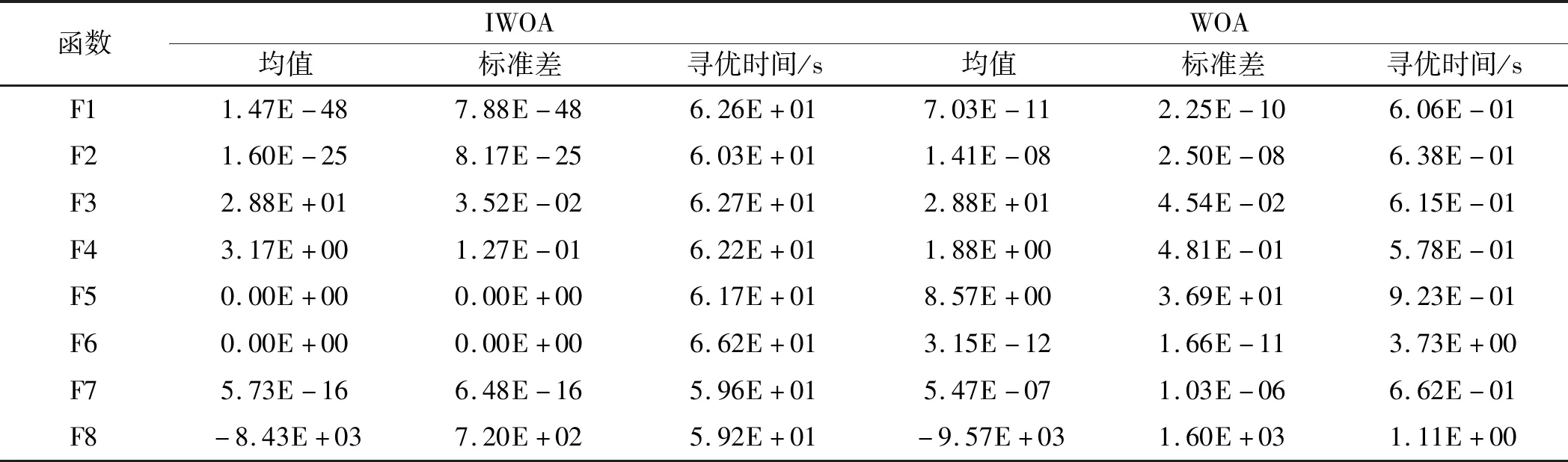
表2 实验结果对比

分析表2结果可知:

在8个测试函数中,IWOA算法的寻优能力比WOA算法要好;其中,F5和F6作为非线性多模态函数,一般情况下很难找到全局最优解,而IWOA算法不仅短时间内找到了最优解,并且达到了理论值;

从优化均值和标准差来看:IWOA算法明显优于WOA算法,因此,IWOA算法拥有更高的收敛精度和更好的寻优能力;

从运行时间来看:IWOA寻优时长要高于WOA,这是因为IWOA在引入余弦控制因子和正弦时变自适应权重系数后,增加了算法的复杂度,进而增加了寻优时长。

3 试验与分析

3.1 试验流程

此处的被测样机型号为东方红4LZ-9A2联合收割机,其发动机转速为780 r/min,联合收割机所有工作部件空载工作。信号采集装置为东华测试的DH5902型动态信号测试分析仪。传感器采用东华测试的IEPE压电式加速度传感器。

该试验的装配质量问题为人为手动注入,具体类型和影响分别为:(1)搅龙未对中,引起积粮和搅龙堵塞;(2)割刀未对中,造成收割机工作过程中漏割和割刀堵塞;(3)割刀传动压紧轮松动,造成割刀的动力不足。

装配质量问题的故障注入如图1所示。

图1 故障注入

笔者通过采集振动信号检测联合收割机装配质量情况,将随机振动信号时域频域特征和分解后的信息熵融合作为特征向量,利用IWOA-LSSVM模型对其进行分类。

联合收割机装配质量检测流程如图2所示。

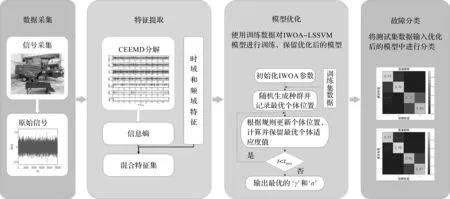
图2 装配质量检测流程图

由图2可知,联合收割机装配质量检测具体步骤如下:

(1)对联合收割机注入装配故障问题并进行信号采集;

(2)对原始信号进行样本划分,并使用CEEMD进行分解,得到若干IMF分量;

(3)利用相关系数选取IMF分量,提取各分量的信息熵和信号的时域频域特征,融合为混合特征集作为最终特征向量;

(4)将训练集数据输入IWOA-LSSVM中进行训练,得到最优模型并保存;

(5)将测试集数据输入优化后的LSSVM中进行分类。

3.2 IWOA-LSSVM的模型建立

最小二乘支持向量机的正则化参数γ和核函数参数σ直接影响着模型的分类准确率,因此,笔者使用IWOA对γ和σ进行优化。

IWOA-LSSVM模型如图3所示。

图3 IWOA-LSSVM流程图

由图3可知,IWOA-LSSVM具体流程如下:

(1)初始化算法参数,设置种群数量N,最大迭代次数tmax,对数螺旋常数b,随机数l等参数;

(2)在解空间内随机产生种群,将最小二乘支持向量机的分类精度误差作为个体的适应度函数,计算每个个体的适应度值,以适应度最优位置作为目标位置;

(3)更新参数a,A,C,l,p,根据规则更新鲸鱼位置得到最优位置,并记录保存;

(4)判断是否达到最大迭代次数,若满足条件,输出最优值和最优个体位置,否则返回步骤(2)继续搜索。

3.3 信号采集

笔者分别对正常信号和故障信号进行采集并进行时频域分析。

正常信号的时域图和频域图如图4所示。

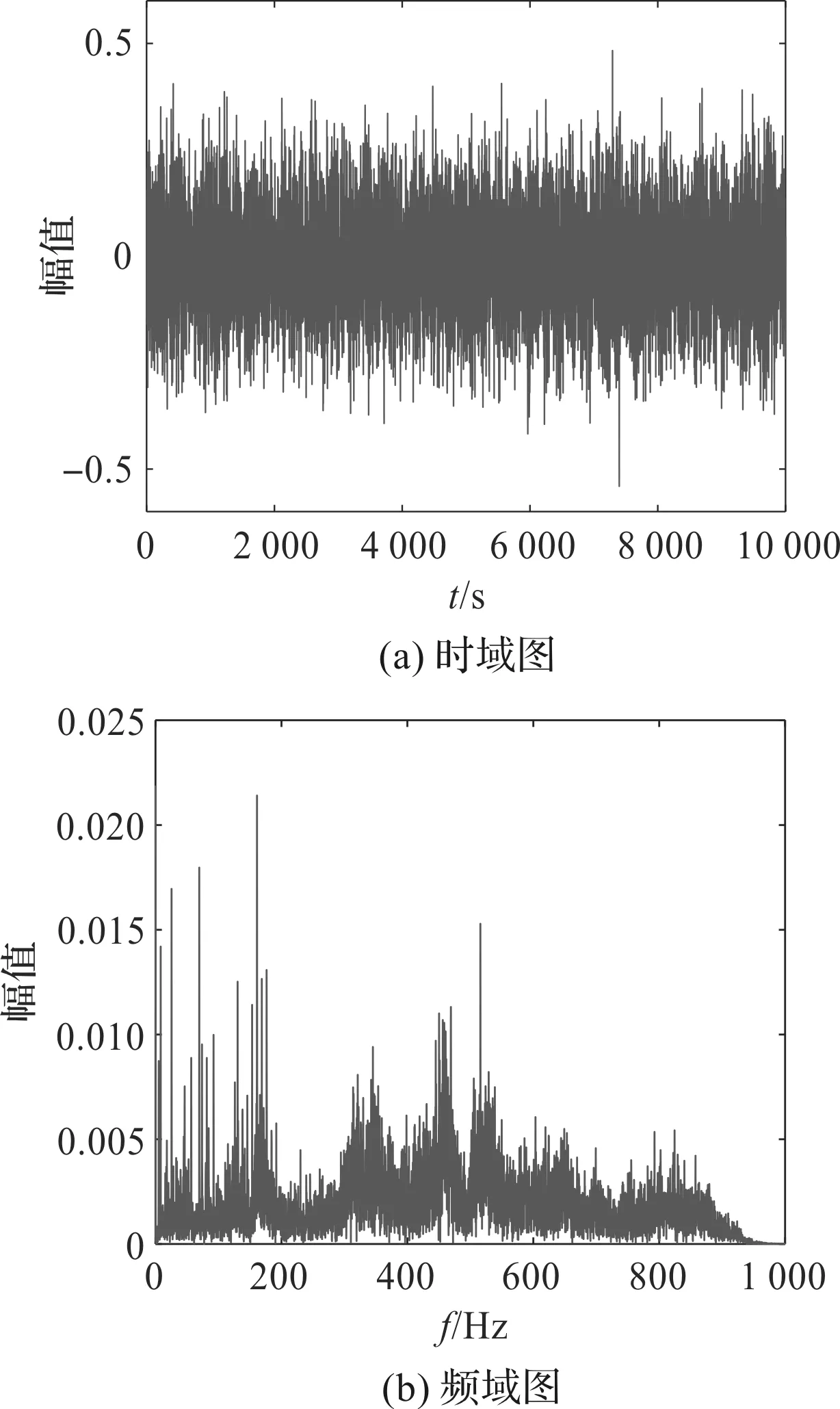
图4 正常信号的时域图和频域图

割刀故障信号的时域图和频域图如图5所示。

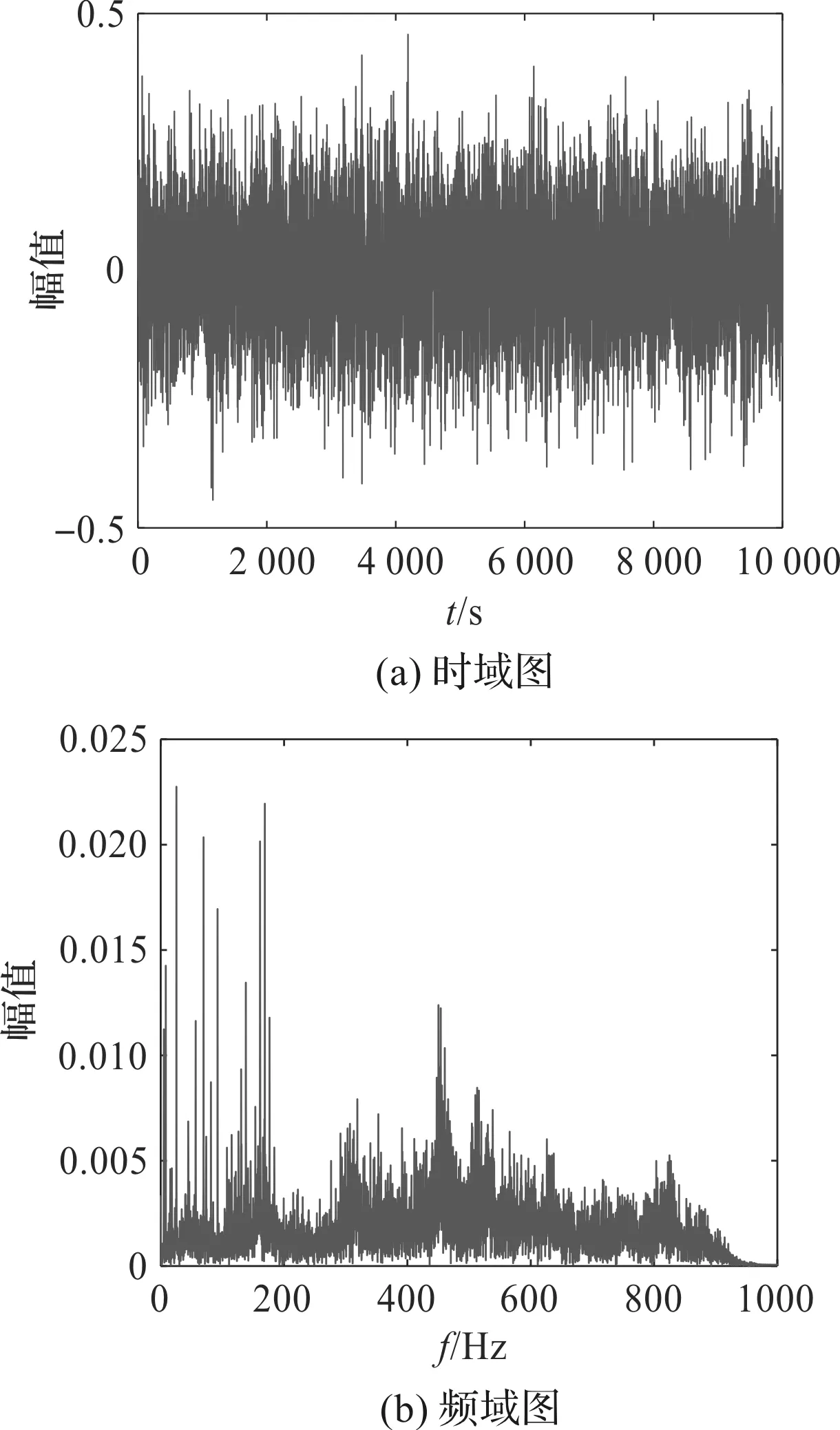
图5 割刀故障信号的时域图和频域图

通过对比图4和图5可以看出:正常信号和故障信号振幅对比不明显,时域部分通过观察难以对信号进行区分,而对比频域图可以发现联合收割机频域成分比较复杂,受到的干扰信号较多。仅靠时域频域特征难以准确对故障信号进行辨别。因此,笔者使用CEEMD对信号进行分解并提取信息熵和时域频域特征构造混合特征集。

3.4 特征提取

笔者使用CEEMD对正常数据和故障数据进行处理,并提取信息熵。单个样本数据长度为2 000。其中,类别1为正常状态;类别2为搅龙未对中故障;类别3为割刀未对中故障;类别4为割刀传动压紧轮松动故障。各类样本长度为200,总样本长度为800。

各样本中,1～150为训练样本,150～200为测试样本,训练样本总数量为600,测试本总数量为200。

其中,分类准确率为各类样本中的正确分类样本数与总体样本数之比。准确率计算方法为:

(19)

式中:ACC—准确率;N—总样本数;TP—将正类预测为正类数;TN—将负类预测为负类数;FP—将负类预测为正类数;FN—将正类预测为负类数。

数据集展示如表3所示。

表3 数据集展示

CEEMD分别对正常状态、搅龙故障、割刀故障和传动系统故障4类信号进行分解,得到多个IMF分量,并使用相关系数进行分析,选择出包含主要故障信息的IMF分量。原始信号与虚假分量、噪声的相关系数比较小,与真实分量的相关系数比较大。

在各工况下,原始信号与各阶IMF分量的相关系数如表4所示。

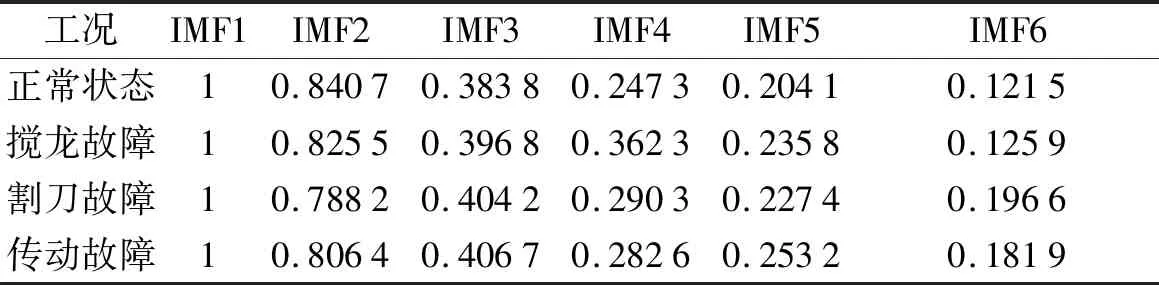
表4 相关系数表

在各工况下,原始信号与IMF6的相关系数均小于0.2,因此,笔者只对前5个IMF分量进行信息熵特征提取,将信息熵和信号的峰值、均方根值和波形因子等时域特征以及中心频率、频率均方根和频率峭度等频域特征融合为混合特征集,作为最终的特征向量。

3.5 基于IWOA-LSSVM的故障识别

笔者使用训练集对IWOA-LSSVM进行训练,利用测试集来验证已训练模型的精度。

为了验证笔者所提出的优化算法的有效性,笔者将其与粒子群算法(PSO)、遗传算法(GA)、WOA这3种方法进行试验对比。其中GA参数设置:p1=0.6,p2=0.01;PSO参数设置:c1=0.5,c2=0.3,w=0.9;4种算法的种群个体总数均设置为30,最大迭代次数为100。

各方法在使用不同特征时的分类准确率如表5所示。

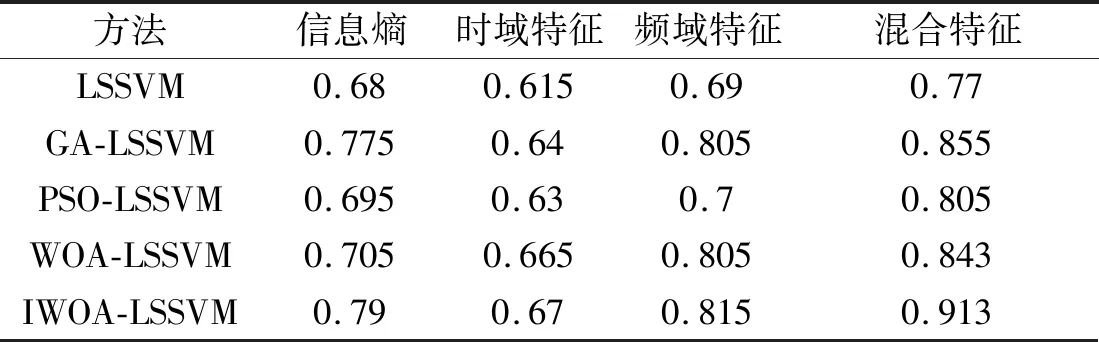
表5 使用不同特征的分类准确率 (%)

从表5可以看出,使用各类单一特征时,分类的准确率要低于使用混合特征集时的准确率。这是由于联合收割机振动信号比较复杂,振动测点的信号由多个部位振源激励耦合,振动测点的信号容易受到其他部位振动的干扰。

因此,使用单一特征无法准确识别出故障类型,笔者使用混合特征集作为最终的特征向量。

笔者使用混淆矩阵(confusion matrix)将测试集的分类结果可视化。各类方法测试集的混淆矩阵如图6所示。

图6 4种方法的混淆矩阵

从图6可以看出:测试集的4类样本中,类别1和类别2的分类准确率较高,类别3和类别4不易区分,分类误差较大。

图6(a)为使用PSO优化LSSVM的混淆矩阵,其中类别3的分类效果较差,有20个样本被误分为类别4;

图6(b)为使用GA优化LSSVM的混淆矩阵,其中类别3的分类准确率相比于PSO算法有所提高;

图6(c)为使用WOA优化LSSVM的混淆矩阵,其中类别3分类效果最差,有14个样本被误分为类别3;

由图6(d)可知:相比于WOA算法,IWOA对类别2、类别3和类别4的辨识度均有所提高,其中类别3的分类准确率提升约15%。

采用各类方法的适应度曲线如图7所示。

图7 适应度曲线

从图7可知:IWOA算法适应度值可以达到0.095,迭代至15次左右已找到最优解,且趋于稳定;与其他算法相比,IWOA不仅收敛速度最快,适应度值也最优。

因此,IWOA可以用于联合收割机的装配质量检测。

为了避免随机因素的干扰,笔者对所提出的模型进行稳定性和泛化能力分析,构建不同的测试集对各类方法进行10次试验,并记录平均准确率和标准差。

10次试验诊断结果如表6所示。

表6 10次试验诊断结果

10次试验诊断准确率如图8所示。

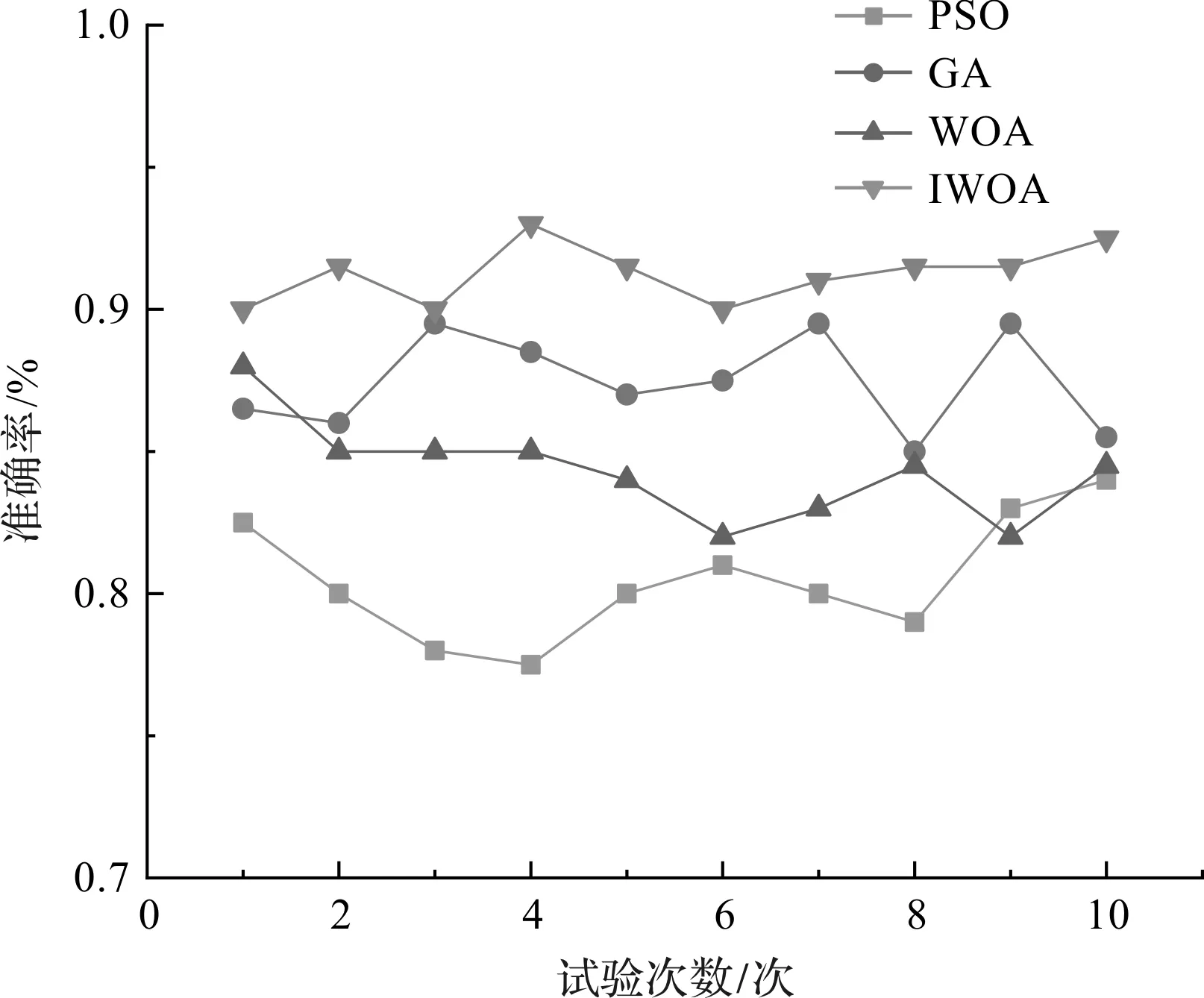
图8 10次试验诊断准确率

由表6和图8可以看出:笔者所提方法的平均准确率达到91.3%,相比于WOA提升了7%,说明WOA在迭代过程中无法很好地平衡局部和全局搜索能力,容易过早收敛,陷入局部最优;PSO平均准确率最低,仅为80.5%,远不如笔者所提方法;GA平均准确率虽然略高于PSO和WOA,但标准差较高,为1.63%。

笔者所提方法标准差仅为0.98%,相比WOA降低了0.68%,说明稳定性更好。

试验结果证明,笔者所提出的CEEMD-IWOA-LSSVM模型可以有效地识别联合收割机的装配故障类型。

4 结束语

针对联合收割机装配质量检测方面存在的不足,笔者首先采用IWOA对LSSVM进行了优化,并将其与CEEMD相结合,构建起了联合收割机装配质量检测模型,并将其在东方红4LZ-9A2联合收割机上进行了试验,以验证检测模型的有效性。

主要研究过程及结论如下:

(1)针对WOA易早熟、搜索能力不平衡等问题,引入非线性控制因子和自适应权重进行了改进;通过8种通用测试函数,验证了改进算法的一般适用性,其整体优化效果优于WOA算法;

(2)笔者对联合收割机的装配质量检测问题进行了研究,提出了一种基于CEEMD信息熵提取、时频特征融合和IWOA优化LSSVM相结合的联合收割机装配故障诊断方法;

(3)通过试验验证了收割机装配质量检测模型的有效性。

由对比分析结果可知,笔者所提方法虽然取得了最好的诊断效果,但91.3%的准确率仍存在提升空间。由于特征提取方法对诊断结果的影响较大,且数据量、模型迭代次数和批量样本数均会对最终结果产生极大影响,目前的模型仍存在一定的优化空间。

因此,针对以上优化结果,下一步笔者的研究思路包括:(1)增加故障类型和批量样本数量,提高模型的泛化能力;(2)使用更为先进的特征提取方法,提高诊断结果的准确率。