基于SVM的精密轴系成功子样数据包络分析

赵 雁，黄玥莹，王雅梦，徐 俊，柴灵芝，潘钢锋

（洛阳轴承研究所有限公司，河南 洛阳 471039）

1 引言

随着我国航天事业的快速发展，对精密轴系的运转性能、寿命及可靠性提出了更高的要求。然而，在对精密轴系开展寿命试验时，存在试验周期过长（3年以上）、无法加速试验、产品样本少的问题。因此，为了通过地面试验样本发现新研产品的问题，对新研产品进行筛选、优化，提高产品可靠性，有必要对精密轴系进行成功子样数据包络分析。

Charnes等提出了一种基于效率评价的数据包络分析方法，把单输入、单输出的工程效率概念推广到多输入、多输出同类决策单元的有效性评价中，避免主观因素、减少了分析误差。徐嫣等通过成功数据包络分析对航天产品进行质量管理和风险控制，并对产品后续生产进行指导。肖支才等利用自助法，通过Sigmoid类型的Boltzmann函数拟合修正传统的样本经验分布函数，对原始数据进行再抽样，将小样本问题转换为大样本问题再进行分析处理。然而，如果不能确定特性之间是相互独立的，需要考虑特性间的相关性，就需要借鉴多元控制理论图。谭超通过对多元控制图性能研究，分析了多元控制图在工程实践中的应用。多元控制理论图其理论基础是特性服从正态分布，因此采用传统的控制图方法进行包络分析时，往往需要先对特性的正态分布进行检验。

通过对前人的研究成果分析，可以发现目前数据包络分析方法存在只满足服从正态分布的特性，且不适用于小样本、多特性子样分析的问题，本文提出了一种基于支持向量机（Support Vector Machine，SVM）的精密轴系成功子样数据包络分析方法，该方法利用先前成功的样本信息，实现小样本、多特性数据包络分析，其训练样本不需要失败的样本，更适合多型号小批量研制模式的精密轴系，并通过试验验证了该方法的有效性。

2 基于SVM的精密轴系成功子样数据包络分析

基于SVM的精密轴系成功子样数据包络分析采用支持向量机计算核距离，通过对比新研样本核距离与成功子样核距离，判断新研样本是否在成功子样包络范围内，从而达到评估产品是否能满足任务要求的目的。分析方法流程如图1所示。

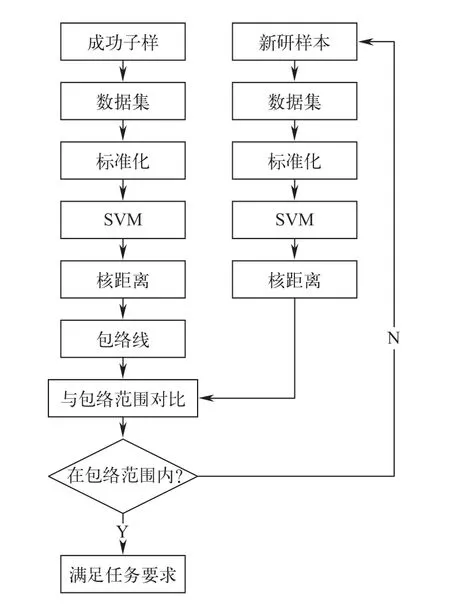
图1 流程图

2.1 SVM

SVM求解核距离的目的是寻找一个最优分类超平面。在分类问题中，超平面被用于确定正常样本和异常样本的边界，如果将超平面看作包络面，则可以把样本包络在尽可能小的多维空间内。因此，目标问题转变成求解含有所有样本数据容积最小的超球的中心O和半径R。求解约束为

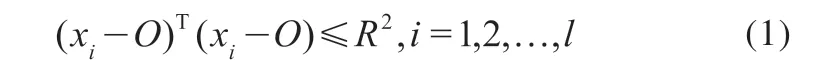
式中，x为训练样本，x∈R；l为训练样本数。

该问题可通过拉格朗日乘数法求解，通过采用高斯径向基函数作为核函数得出数据的边界，由支持向量求得的边界紧凑且灵活。

2.2 核距离的控制图（K图）

采样点和中心之间的距离是用来监控的有效指标，距离越远，说明参数偏离正常值的可能性越大，边界是正常与异常状态之间的边界值，从式 (1) 可知，新样本z与超平面中心O之间的核距离为

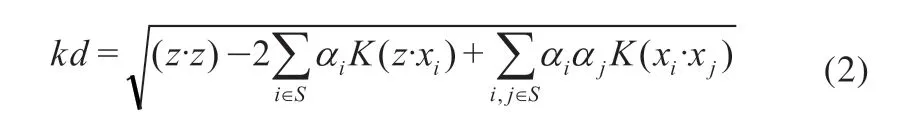
式中，K (·)表示采用高斯径向基函数的核函数。

高斯径向基函数为

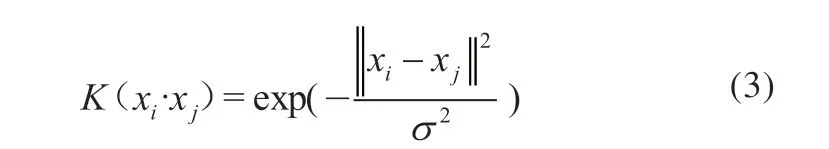
式中，σ为常数。

采用径向基函数构建K图的关键是确定常数σ，σ决定了支持向量集，σ越小，支持向量越多，超平面体积越小；σ越大，支持向量越少，超平面体积越大，利用启发式程序可以确定σ值。

部分正态分布的样本集，采用支持向量识别出最佳的边界。核距离的控制图（K图）如图2所示，图上的水平线相当于边界的核距离，可用K图监控关键参数、识别异常点而不受分布假设和样本量的限制。

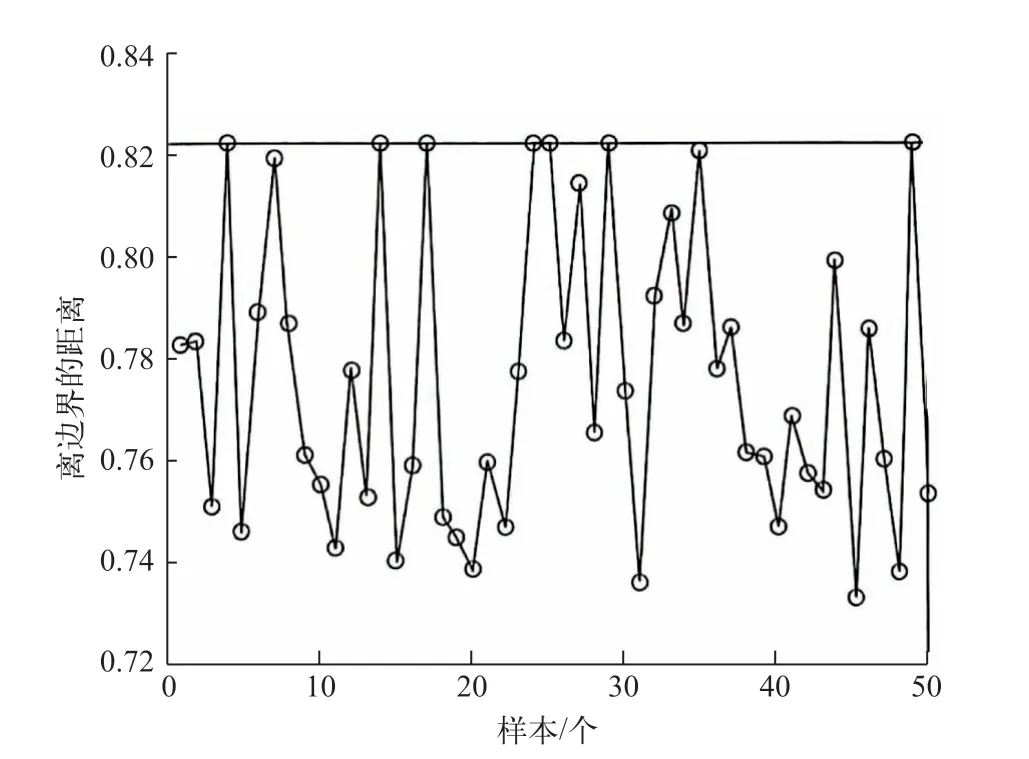
图2 K图

3 试验验证及数据分析

采用12组XX型号精密轴系进行地面试验，试验过程中通过运行状态检测及分析系统对试验样本运转性能进行全程监测（电流、功耗、温度和振动等），如图3所示。

图3 XX型号精密轴系地面试验

在38个月的地面试验过程中，试验样本运转性能良好，可以满足整机要求。地面试验完成后，对试验样本进行了拆解分析，通过拆解确定轴承沟道接触正常、润滑良好，最终确定试验的12组XX型号精密轴系为成功子样。

3.1 关键参数及特性确定

根据精密轴系运转性能主要受旋转支撑系统影响的特点，在关键参数的选取中重点围绕旋转支撑系统展开，并将关键参数分为关键性能参数（见表1）和关键工艺参数（见表2）。

表1 关键性能参数

表2 关键工艺参数

3.2 获取子样数据集

采用地面试验12组成功子样数据集和6组新研样本数据集，对关键参数进行测量、记录。

3.3 标准化处理

对12组成功子样和6组新研样本数据用Z-score标准化法进行标准化处理，标准化处理后的数据为

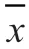
标准化处理目的是消除量纲和大小对数据的影响。

3.4 结果分析

（1）成功子样支持向量

采用高斯径向基函数（C=0.1），通过启发式程序，求出最优的σ =0.282 8；采用二次线性规划求解α，得出支持向量见表3。

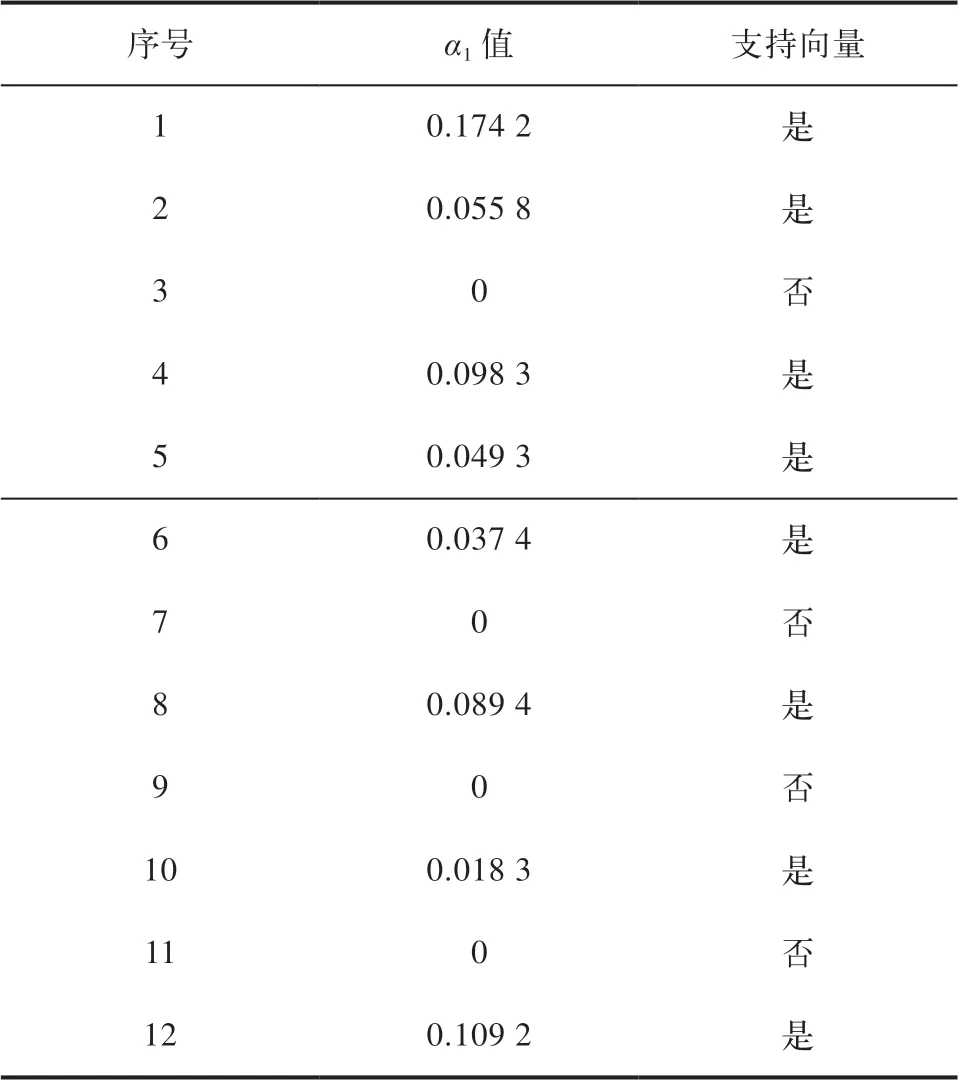
表3 成功子样支持向量求解结果

（2）成功子样核距离

由支持向量得出产品成功子样数据包络线

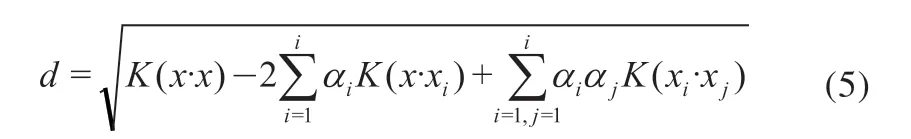
求解结果见表4，由表可知，基于成功子样数据包络线得出的包络线核距离为0.479 7。

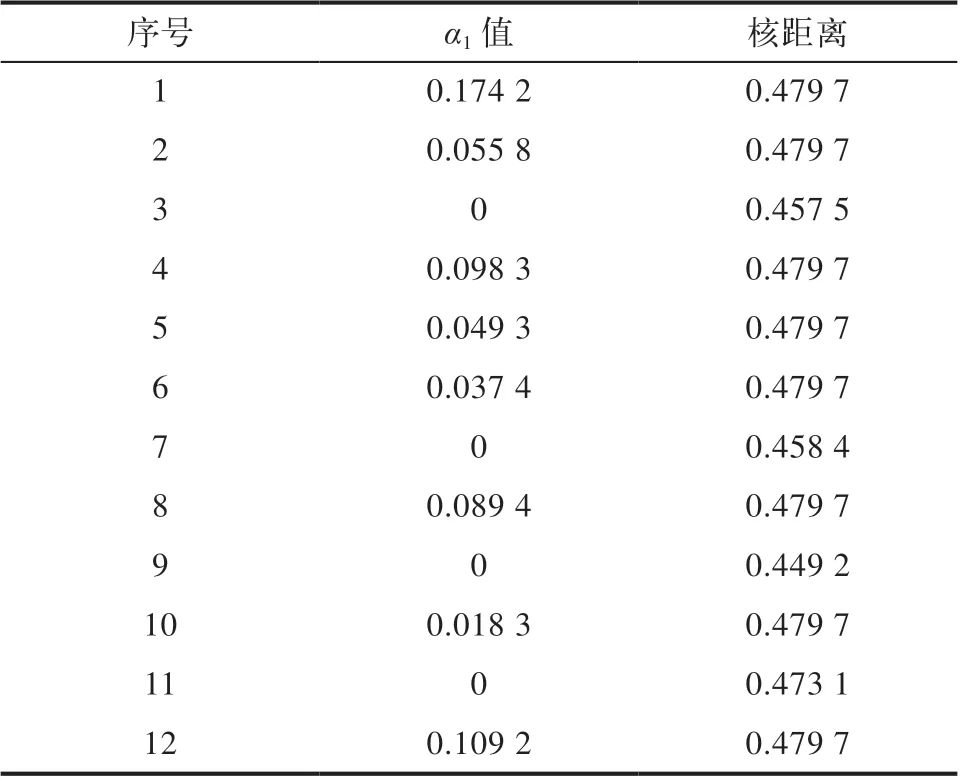
表4 成功子样核距离

（3）新研样本支持向量与核距离

求解结果见表5。

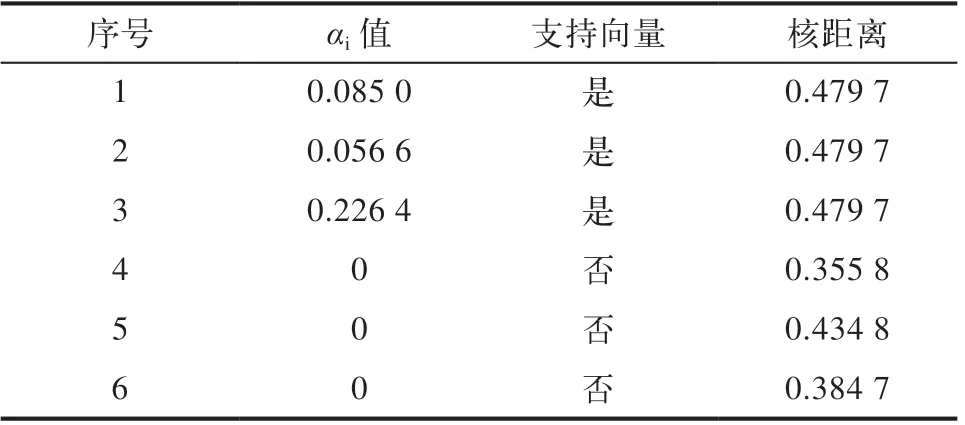
表5 新研样本支持向量求解结果与核距离

（4）形成K图

如图4所示，蓝色分界线左侧为历史成功子样数据，右侧为新研样本数据。

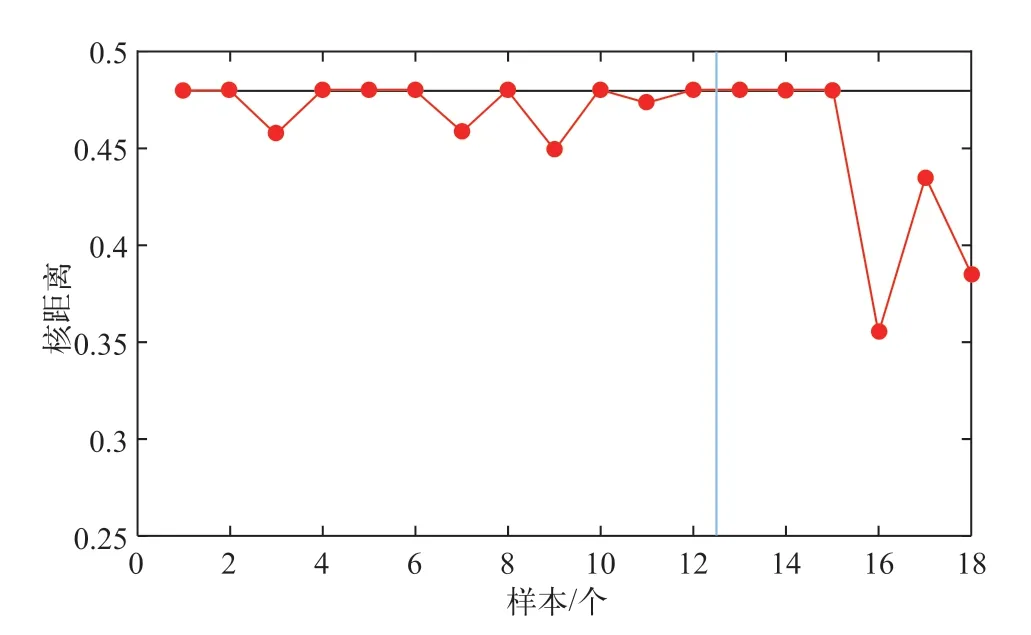
图4 基于SVM的产品成功数据包络线

将新研样本数据与历史成功子样数据包络范围进行对比可知，新研样本在历史成功子样数据包络范围内，表明新研样本在产品质量稳定性与可靠性上与成功子样达成一致，满足任务要求，具备执行任务的能力。

4 结束语

成功子样数据包络分析方法基于数据理论分析和统计过程控制理论，通过分析有限子样的数据表征，对产品能否完成任务要求进行判断。分析对象包含了产品的性能、工艺参数，体现了面向结果和过程的质量控制思想。