基于PFA 算法的动目标特性分析

贺雪莉

（兴义民族师范学院 信息技术学院， 贵州 兴义 562400）

一、引言

合成孔径雷达（Synthetic Aperture Radar，简称SAR）是现阶段应用广泛的高分辨率成像雷达，条带式、扫描式以及聚束式等是常用的传统SAR 成像模式[1]。然而，由于受限于图像帧的更新速率，通过这些模式都只能得到静态的目标图像，无法对运动目标的轨迹和速度等信息进行捕捉，甚至无法通过静止图像区分场景静止目标与动态目标[2]，但在实际的应用中，运动目标所包含的信息也具有十分重要的研究意义和价值。PFA 算法是一种经典的聚束SAR 成像处理算法，它的主要步骤包括距离和方位两个一维插值以及两维Fourier 变换，是一种适合小场景高分辨率成像的高效成像处理算法[3]。

通过对静止目标和运动目标的回波数据对比分析，从数学角度推导运动目标对回波产生的影响，即运动点目标回波信号的包络和相位存在的特性。接着通过对PFA 处理后的静止目标和运动目标回波数据分析，探索含有运动目标的回波处理后具有的特点。最后通过对PFA 处理各个阶段的距离徙动线对比，总结最终结果的特征。基于PFA 算法的动目标特性分析能够为后续的目标检测识别奠定理论基础，在视频SAR 成像处理算法研究中也发挥着重要的作用，因此具有研究价值。

二、运动目标回波特性分析

聚束SAR 成像的几何模型如图1 所示[4]。

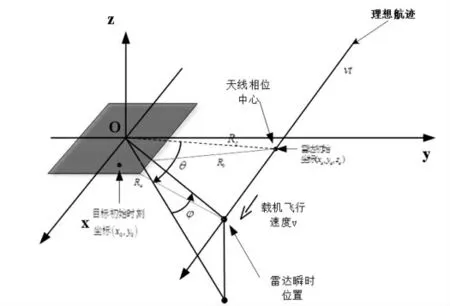
图1 聚束SAR 成像几何模型

以场景中心O 为坐标原点建立XYZ 坐标系，其中视线方向的地面投影为Y 轴。雷达运行的轨道与x 轴平行的轨道线之间的夹角是θs，即为斜视角度，正侧视情况时无斜视角，即θs=0。为了公式推导更具有普遍性，本文以θs不为0 的斜视情况进行分析，设雷达平台是以速度v 沿轨道匀速运动的。雷达天线相位中心（APC）的实时坐标为（xa,ya,za），其中xa与ya均和方位时间t 存在线性关系，孔径中心时刻的坐标为（0，yc,zc），其对应的瞬时俯仰角和方位角分别为和θ（角度和θ均为方位时间t 的函数）。场景中存在目标P，起始位置为（x0,y0,0），沿X 轴与Y 轴的运动速度为vx和vy[5]。因此雷达天线相位中心到场景和目标的实时距离Ra和Rt，以及孔径中心时刻天线相位中心到目标的瞬时距离表示为：

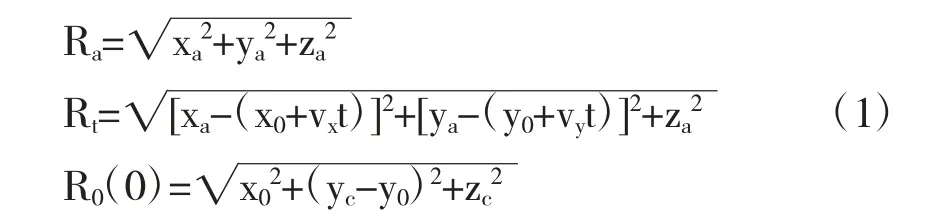
雷达发射线性调频信号（Linear Frequency Modulation,LFM）[3]，经过解调和匹配滤波①后得到运动目标的回波信号为[2]

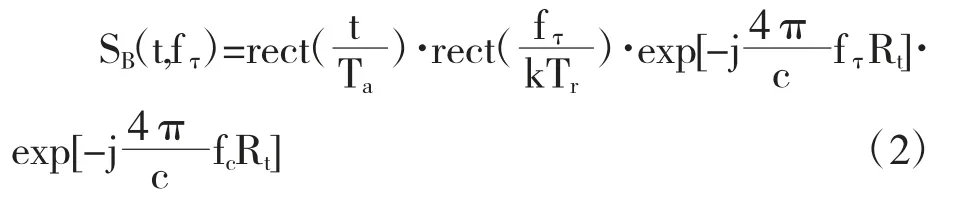
为了分析运动目标的回波信号，需要得到目标静止时的回波信号来做对比，在图1 中，目标静止时的位置始终位于（x0,y0,0），则雷达天线相位到静止目标的实时距离R0为：

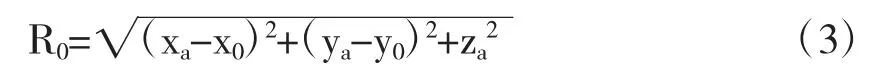
同理，通过对原始回波信号进行解调和匹配滤波后的到静止目标的回波信号为：

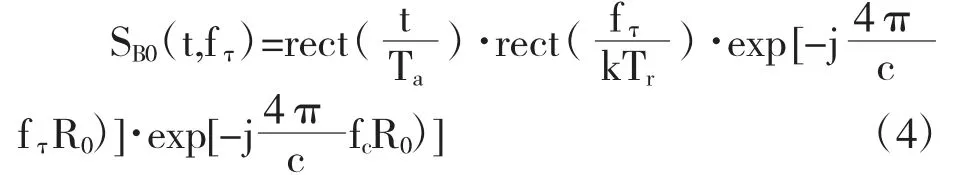
对比运动目标和静止目标天线相位中心到目标的实时距离的和，对和分别在t=0 处作泰勒展开，能够得到两者关于方位时间t 的二次函数关系如下：

其中常数a、b 表示为：

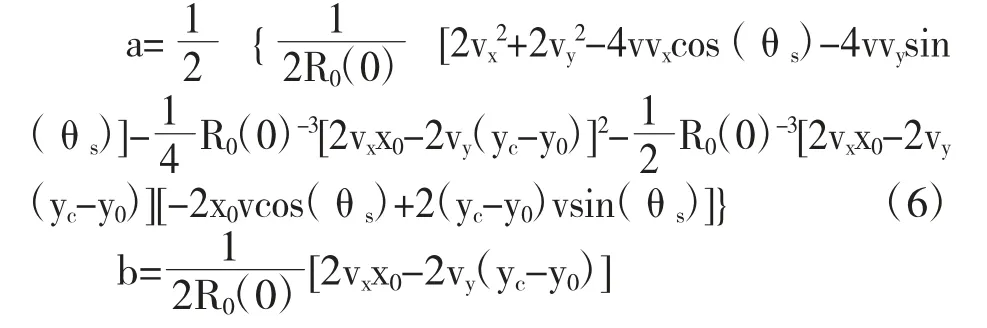
将式（5）和式（4）带入到式（2）可以得到运动目标回波信号关于静止目标回波信号的表达式，对表达式进行拆分，得到运动目标的回波信号和静止目标的回波信号的包络φ和相位具有如下关系：

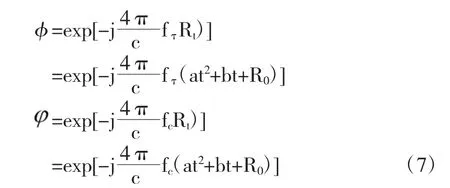
分析（7）式可知，由于是时间t 的二次函数的关系，因此与静止点目标相比较，运动点目标的包络存在线性走动和距离弯曲，相位存在中心移动和方位调频率改变的变化。

三、基于PFA 算法的运动目标特性分析

对式(2)和(4)所表示的动目标和静止目标的回波信号分别进行运动补偿，得到PFA 处理前的回波信号为

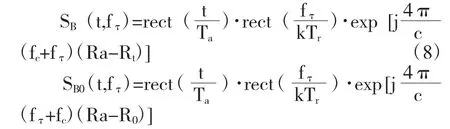
在平面波前假设的前提下，将式（1）带入式（8）得到运动补偿后的动目标和静止目标回波信号分别为

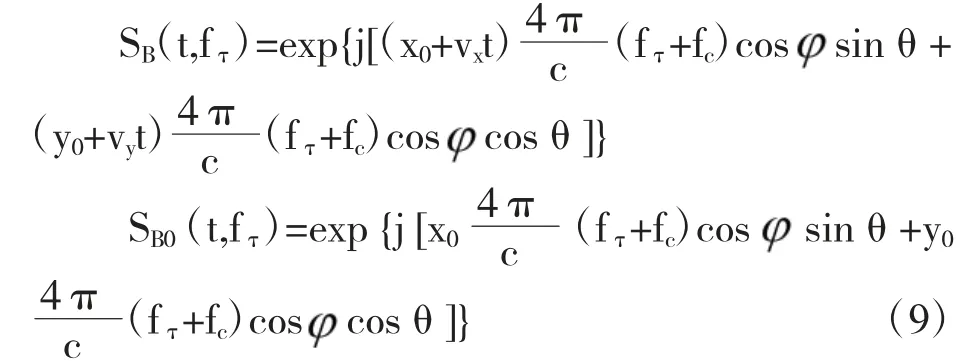
分析补偿后的回波信号表达式可知，和静止目标相比较动目标的回波信号增加了与目标移动速度vx和vy有关的两项耦合项，提取耦合项可以的到运动目标和静止目标运动补偿后的回波信号有如下关系

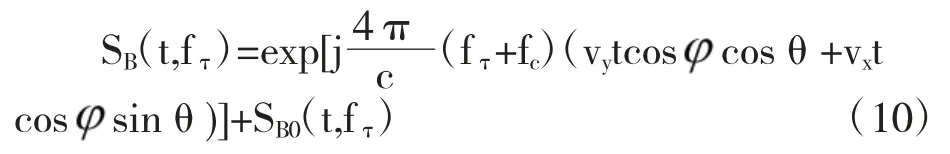
根据表达式（10），对动目标回波信号进行PFA 处理时的分析可以分为静止点目标和附加的运动项两部分来分析，便于清楚的显示出运动目标的特性。从图1 的分析，可以得到如下几何关系

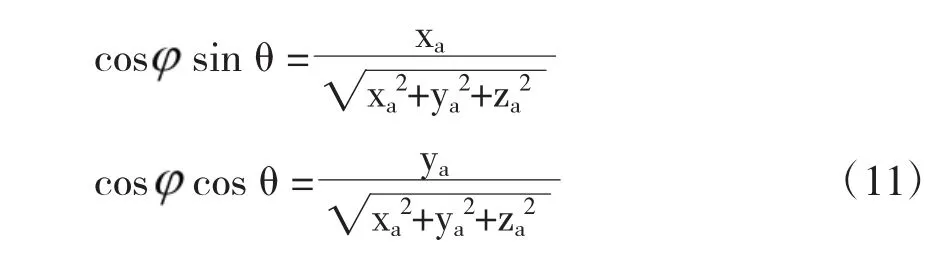
将式（11）的几何关系代入式（10）中，并做距离向傅里叶变换和泰勒展开得到运动点目标的距离徙动曲线为

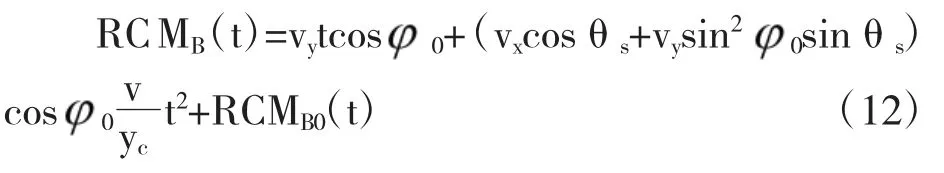
分析式（12）得出如下结论，和静止目标相比较，动目标回波信号的距离徙动在原有的线性走动和高阶距离徙动弯曲的基础上，还存在额外的与点目标运动速度有关系的距离徙动的线性走动和二阶徙动弯曲项。

在对回波信号进行PFA 处理之前，需要注意在斜视情况下，斜视角θs≠0，此时回波信号的距离徙动曲线为式（12）所示，tanθ 的取值为

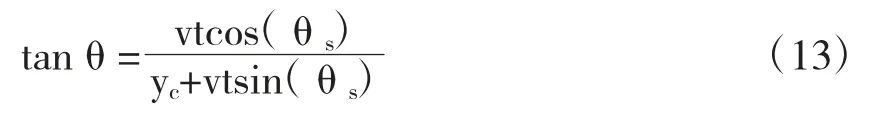
（一）距离向PCS 变换

对运动目标斜视情况下的距离向插值，也是对回波信号乘以尺度变换公式

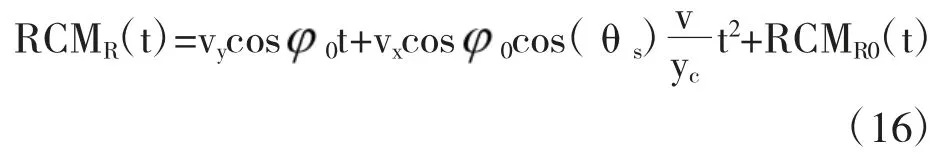
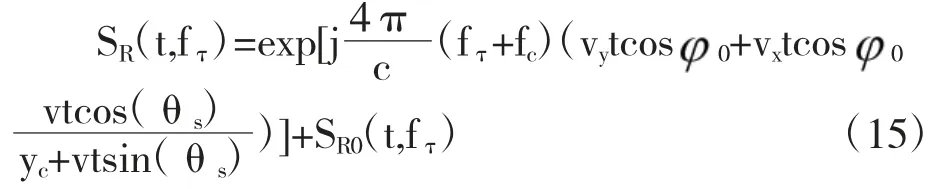
分析表达式（16）可知，和静止目标情况相比较，斜视情况下经过距离向插值处理后的动目标的距离徙动曲线还存在距离向的线性走动，即距离向没有完全校正，此外还有残余的和目标方位向运动速度有关的二次项没有校正。

（二）方位向插值变换

斜视情况下由于tanθ 是非线性的，于是在进行方位向尺度变换之前，先对回波（15）做与距离频率不相关的方位重采样，使tanθ 线性化，得到在tanθ 域是均匀采样的信号。重采样等效于作变量替换tanθ=Ωcosθst，重采样后再对回波信号进行方位向尺度变换即可实现方位向插值，得到斜视情况下方位向插值后的回波信号

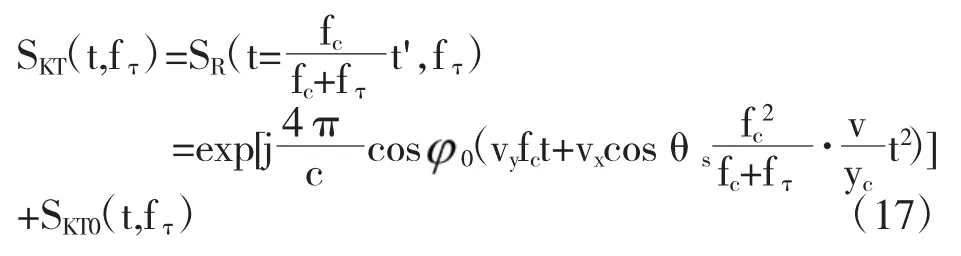
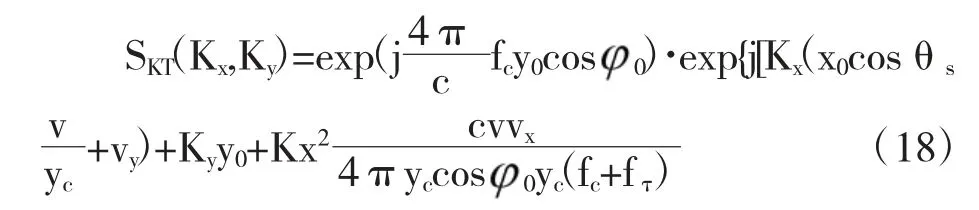
其中Kx和Ky的取值分别为

而静止目标经过PFA 处理后的空间波速域回波信号为

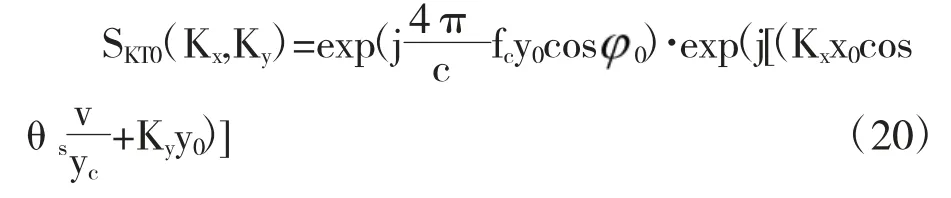
比较斜视情况下静止目标和运动目标的PFA处理后回波信号的空域表达式可以发现，由于其项的系数一直为常数，两者在方位空间频域的变化一致，均是保持不变的，可以得到结论，无论是静止目标还是动目标，经过PFA 处理后的回波信号的距离向的偏移都能被完全校正，不会存在距离门的跳变。通过对分析，可以看出，PFA 处理后的动目标的回波信号还存在与目标距离向移动速度有关的方位频偏以及由方位频率的二次项引起的散焦现象，此外一次方位空间频率还和目标的距离向运动速度有关系，说明目标存在方位向移动。

四、实验验证与结论分析

静止点目标仿真基本雷达参数如表1 所示[6]。

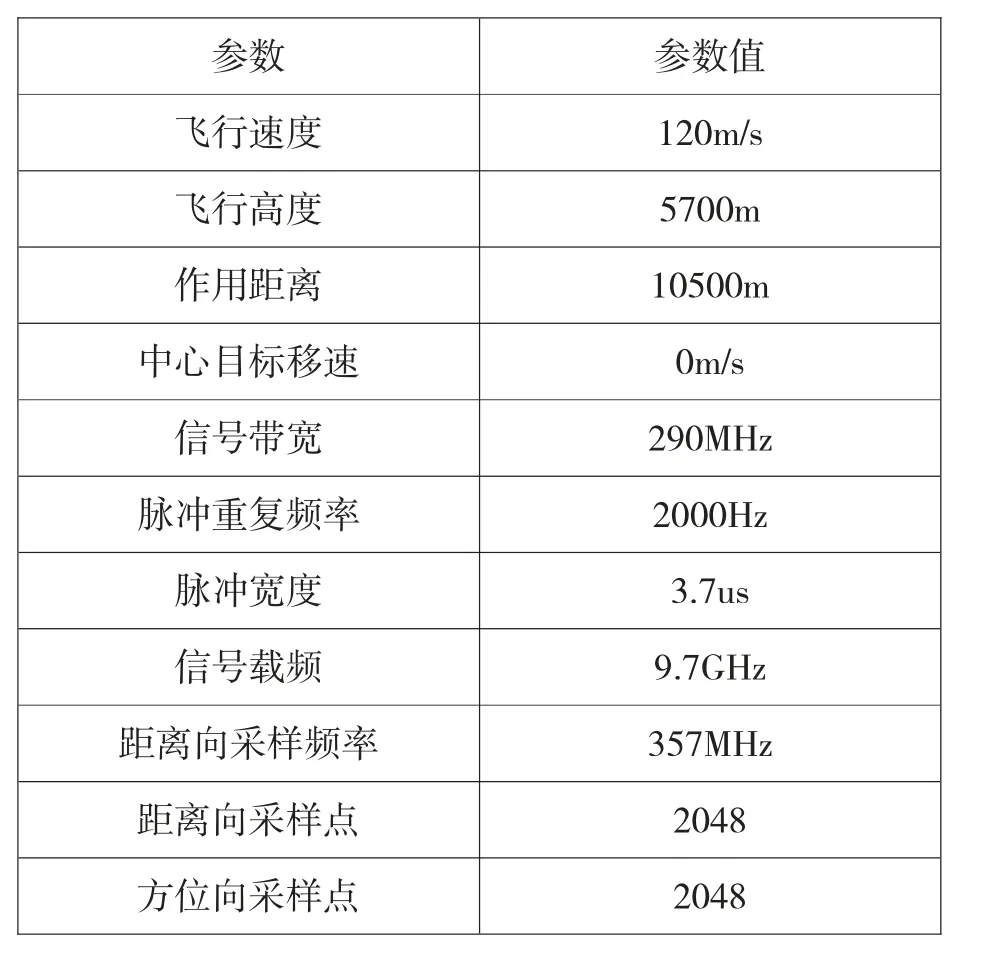
表1 点目标仿真基本雷达参数

图2 PFA 处理后静止点目标回波结果图

从上述处理结果可以看到，距离向处理后校正了距离徙动的二次及更高次，达到了预期消除距离向快时间变量的耦合的目的，此时的距离徙动是一个线性函数，没有弯曲；做完方位向尺度变换后，距离向尺度变换没有校正的线性走动也被完全校正，点目标聚焦。

根据公式（20）可以推算出，对移动点目标做PFA 算法处理后的回波信号中包含有方位向一次项和二次项，其中空间频域的方位向二次项会引起目标散焦现象。保持静止点目标仿真参数不变，将中心目标运动速度调整为10m/s，接下来分别对运动的三种不同轨迹进行分析，沿x 轴运动、沿y轴运动以及与x 轴成45 度角沿两个方向同时运动，假设沿每个方向的移速均一致。得到如下图所示的仿真结果图。

目标的运动会对SAR 信号产生两个方面的影响，影响之一是会在方位向引入一个相位误差，导致图像发生方位散焦；影响之二是会产生额外的距离徙动，在SAR 成像过程中无法得到补偿，而且经过成像算法处理后，残留距离徙动效应还会导致图像距离向出现二次散焦[7]。分析上述三幅结果图可以验证以上结论，在图3 所示的PFA 处理后的回波中，没有由于项，因此不存在由于带来的项，故不存在方位向移动，但是由于存在项，因此不为0，故回波信号存在方位向空间频率的二次项，即图3（b）中表现出来的点目标散焦现象。在图4 所示的处理后的回波数据中，当目标只有轴移动时，那么此时由于 带来的散焦不再存在，而由于产生的项导致处理后的回波存在方位向移动，即图4（b）中捕捉到的良好聚焦后的移动点目标。当目标既存在轴的移动又存在轴的移动时，那么根据公式（20），此时处理后的回波数据不仅会出现方位向移动，同时也会存在散焦现象，既图5（b）中所示的结果。

图3 沿x 轴运动目标经PFA 处理后的回波结果图

图4 沿y 轴运动目标经PFA 处理后的回波结果图

图5 沿x 轴成45 度角运动目标经PFA 处理后的回波结果图

从上述结果分析可以得到如下结论：无论是静止目标还是移动目标，经过PFA 处理后的回波信号距离向的偏移都能被完全校正，不会存在距离门的跳变；当回波信号中含有沿x 轴运动的点目标时，做PFA 处理后还存在与距离向目标运动速度有关的方位频率二次项引起的散焦现象，当回波信号中含有沿y 轴运动的点目标时，处理后的回波中包含与方位向目标运动速度有关的方位向移动，验证了表达式(20)。

注释：

①时域上的脉冲压缩可以通过在频域中将回波信号的频谱与发射信号频谱共轭相乘实现，这样计算可以简化很多，把这种频域上的脉冲压缩称为匹配滤波。