Mg–Gd–Y–Zn稀土镁合金应变调节机制研究
韩艳彬,蒋少松,李阳
塑性成形
Mg–Gd–Y–Zn稀土镁合金应变调节机制研究
韩艳彬1,蒋少松2,李阳2
(1.中航西安飞机工业集团股份有限公司,西安 710089;2.哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001)
在微观尺度上研究Mg–5.4Gd–1.8Y–1.5Zn合金的应变调节机制。将拉伸试样变形至应变为6%,采用基于互相关分析的高分辨EBSD技术测量材料内部的刚体转动张量以及几何必需位错密度。Mg–Gd–Y–Zn合金主要由基面<>位错以及锥面<+>位错调节应变,即使在软取向晶粒内,锥面<+>位错也会大量出现。当发生基面–基面位错的滑移转移与基面–锥面位错的滑移转移时,相邻两晶粒滑移系之间的Luster–Morris因子很高(>0.78)。随着不同滑移系施密特因子的升高,晶粒内的位错密度逐渐降低。这一反常现象可以归因于硬取向晶粒变形需消耗更多的应变能,而这部分应变能以位错密度的形式储存在晶粒内。
应变调节;稀土镁合金;HR–EBSD;滑移转移;位错密度
镁及镁合金因其低密度与高比强度的特性,在航空航天以及汽车工业领域中具有广阔的应用前景[1-3]。镁合金具有密排六方结构及较强的各向异性,室温塑性较差,这主要是因为镁合金不能沿着<0001>晶体学方向变形,轴方向的变形必须通过锥面<+>位错来完成[4-6]。最近的研究表明[7-8],<+>位错为亚稳态状态,极易转化为不可动结构,从而不能协调轴方向的应变。除了位错滑移,镁合金塑性变形还包括一定的孪晶与晶界滑移[9-10],其中,孪晶的存在可以使基体晶体重新定向,从而引发滑移系相对于应力轴的择优取向。
目前,提高镁合金塑性的方法主要包括细化晶粒、添加合金元素以及改善基面织构等[11-13],这些措施可以使变形镁合金的伸长率达到20%~30%[14-15]。Ahmad等[8]研究表明,通过添加适当的合金元素可以防止<+>位错转化为不可动结构,添加稀土元素可以激发镁合金中的<+>锥面位错,从而提高材料塑性[16-20]。Sandlöbes等[16]发现相同的加工条件下,Mg–3%Y(质量分数)材料的伸长率是纯镁试样的5倍。Xu等[21]采用热挤压法实现了Mg–Gd–Y–Zn–Zr合金高强度和高韧性的结合,合金屈服强度达到466 MPa,伸长率达到14.5%,其中,多晶镁中存在应变调节机制,可以使多个晶粒协同变形,每个晶粒内的变形相加,就会产生宏观上的塑性变形。Orozco– Caballero等[9]采用高分辨数字图像相关(digital image correlation)技术研究了AZ31镁合金中的应变调节机制,发现AZ31镁合金中的变形主要依靠基面滑移系以及硬取向晶粒内的非基面滑移来调节,可见,应变调节机制对促进镁合金塑性性能的提升至关重要。现阶段关于稀土镁合金应变调节机制的研究仍然较少,研究表明,纯镁和稀土镁合金在变形机理方面存在一定差异。增强对镁合金塑性变形机理的了解,有助于制定有效的增韧策略,从而提高镁合金的可加工性能。
在应变调节机制分析方法上,目前通常使用透射电子显微镜(TEM)与X射线衍射来测量材料内部应变。TEM具有很高的空间分辨率和良好的应变敏感度,使用汇聚束电子衍射技术甚至可以提取材料内部的全应变张量[22]。TEM只能观察到材料内很小的一部分区域,使用TEM进行统计分析极其困难。X射线衍射技术可以很方便地测量材料内部应变,X射线具有非常好的应变敏感度(10−5量级),但其空间分辨率很差,通常只有几十微米左右[23]。使用同步辐射光源可以将空间分辨率大幅提高到1 μm,但使用这种大型设施很不方便[24-25]。高分辨电子背散射衍射(HR–EBSD)技术的出现,使人们可以通过测量菊池花样晶带轴的偏移量来计算弹性应变张量和刚体转动张量。该技术相较于传统的Hough变换EBSD,取向差分辨率提高了80倍,目前已被广泛应用于测量晶格应变以及位错(GNDs)[23,26-30]。高分辨EBSD的弹性应变分辨率为10−4,角度分辨率为10−4rad,其空间分辨率与传统EBSD一样为50 nm。通过扫描电镜很容易获得材料的菊池花样,高分辨EBSD可以计算材料内部的应变张量与几何必需位错密度,从而进行统计分析。
文中创新性地从微观尺度上定量化地研究稀土镁合金Mg–Gd–Y–Zn中的应变调节机制,通过高分辨EBSD技术对Mg–Gd–Y–Zn稀土镁合金内的晶体取向、刚体转动张量以及几何位错密度进行测量。
1 方法
实验材料为Mg–5.4Gd–1.8Y–1.5Zn(质量分数)稀土镁合金,由中铝由郑州有色金属研究院提供。材料的初始状态为铸态,晶粒尺寸粗大。为改善晶粒尺寸,对稀土镁合金原始铸锭进行了等温多向锻变形。合金锻造前在500 ℃下进行12 h的固溶处理,固溶后分别沿、、轴对材料进行6道次多向锻变形,之后在500 ℃下对合金退火15 min从而消除内部应力。使用电火花线切割对退火态合金进行切割,切取的试样厚度为1 mm、标距宽为2 mm、标距长为4 mm。试样表面采用不同粒度的碳化硅砂纸进行研磨,然后用胶体二氧化硅悬浮液进行抛光。为了获得无应力表面进行电子背散射衍射(EBSD)测试,实验中使用10%高氯酸+90%酒精(体积分数)的电解质溶液对试样表面进行电解抛光,抛光电压设为10 V,温度为−20 ℃,操作时间为100 s。拉伸试样电解抛光后,在室温下使用Deban 2KN原位EBSD拉伸台(见图1a)对材料进行拉伸。拉伸实验在NanoSEM 430扫描电子显微镜内进行,拉伸速率设为1×10−3s−1。原位拉伸台由双螺纹丝杆驱动,可以实时观察材料表面变形情况。拉伸试样变形至应变为6%,EBSD操作电压为20 kV,电流为6.1 nA,步长设置为0.6 μm。
采用Crosscourt 3软件对实验获得的菊池花样数据进行分析。通过比较晶粒内参考菊池花样与测试菊池花样晶带轴的位移,来计算材料内部的应变与几何必需位错密度。参考菊池花样选择在材料内部取向差最小的点。在执行互相关函数之前,每个菊池花样被分为50个方形区域,在每个区域内进行一次互相关计算,如图1b所示。样品内的几何必需位错密度是由Nye位错张量计算得到,Nye位错张量与不同类型的位错密度关系见式(1)。

式中:s为位错的类型;bs为s型位错的伯氏矢量;ls为s型位错的线矢量;ρs为s型位错的密度。以下位错类型被考虑参与计算:基面上的3种类刃型位错,3种类螺型位错;柱面上的3种类刃型位错;锥面上的6种类刃型位错;锥面上的12种
晶粒内部主导滑移系通过晶格畸变转动轴(in grain misorientation axis,IGMA)判定。不论是刃型位错还是螺型位错,位错周围的区域内都存在晶格畸变,位错周围的原子绕一轴线发生偏转,该轴称为Taylor轴。每个晶粒内的Taylor轴由取向数据获得,并在晶体坐标系内极射赤面投影。Taylor轴位于滑移平面之内,并垂直于滑移方向,其表示方法见式(2)。
(2)
式中:s、s、s分别为Taylor轴方向、滑移面法向以及滑移方向。不同滑移系对应的Taylor轴方向如表1所示。通过比较实验测得的IGMA图与给定滑移系统的Taylor轴,进而确定塑性变形晶粒内部开动的滑移系。
拉伸结束后,样品表面的滑移带由配备背散射电子探测器(CBS探头)的FEI Verios 460扫描电子显微镜进行观察,工作距离设定为4 mm,电压设置为10 kV。此外,通过将各个晶粒表面的取向数据导入MATLAB程序中,计算样品表面的理论滑移带。
表1 镁合金内不同滑移系对应的Taylor轴

Tab.1 Taylor axis corresponding to different slip systems in magnesium alloy
材料在塑性变形时,位错在晶粒A内堆积,激发相邻晶粒B内开动滑移系。位错在这2个相邻晶粒内的几何关系可以用Luster–Morris因子'来评估,其定义见式(3)。

式中:为相邻两晶粒内滑移方向之间的夹角;为相邻晶粒滑移面法向之间的夹角。位错在相邻晶粒内的几何关系如图2所示。

图2 相邻晶粒滑移系的几何关系定义
2 结果与分析
对不同取向晶粒的表面形貌、几何必需位错密度分布以及刚体转动张量进行分析。图3a为材料变形后在拉伸轴方向的反极图,图3a对每个晶粒进行了编号。由图3a可以看出,材料组织由几微米至几十微米的晶粒组成。变形后晶粒内存在取向梯度(如晶粒18),表明位错滑移在这些晶粒内开动。图3b为变形后材料的极图,极密度6.1表明材料具有弱织构。晶粒内的几何必需位错密度分布如图3c所示,可以看出不同晶粒间发生非均匀变形,晶粒内的位错堆积在晶界处,特别是三晶粒交界处。根据基面滑移系施密特因子的大小,将用于应变分析的晶粒分为3类:宏观应力几乎平行或垂直于基面,这种情况下晶粒的施密特因子接近于0,为硬取向晶粒;基面滑移系的施密特因子为0.25;晶粒取向有利于基面滑移开动,这种情况下晶粒的施密特因子接近于0.5,为软取向晶粒。

图3 样品拉伸变形至6%后其内部取向以位错密度分布
2.1 不同施密特因子晶粒内的位错调节机制

借助HR–EBSD,晶粒内的几何必需位错密度可以由Nye位错张量来求解。图4c中的XCF峰值平均值表明获得的菊池花样质量适合于互相关函数计算。此外,图4c还给出了晶粒36内的位错密度分布,可以看出,晶粒内发生了不均匀变形,位错容易堆积在晶界处。晶粒36的刚体转动张量如图4d所示,在晶粒右下方三晶粒交界处(晶粒36、37、46)发生了较大变形。图4e给出了沿着–线间的几何必需位错密度。在–线间,晶粒36的位错密度大约在1013m−2左右。由点至点,位错密度急剧增加到1.9×1013m−2,点和点之间较高的位错密度主要是由<>类基面位错和<+>锥面位错构成。此外,沿–线的锥面<+>位错密度与基面<>类位错密度非常接近。柱面位错密度在晶粒36内非常低,大约为1011m−2。因此,三晶粒交界处(晶粒36、37、46)的变形主要由锥面<+>位错与基面<>类位错协调。


图4 拉伸至6%后晶粒36表面的滑移带以及位错密度分布情况

图5 拉伸至6%后晶粒31表面的滑移带以及位错密度分布情况

图7a为晶粒11变形后的背散射电子图像。晶粒11是一个软取向晶粒,其基面滑移系的最大施密特因子为0.48。图7b中,晶粒11表面的滑移带为基面滑移系开动的结果。晶粒11的IGMA分布图表明,晶粒11内基面与锥面滑移系开动。从图7b可以看出,晶粒11与14之间发生基面位错的滑移转移,相邻两晶粒间的Luster–Morris因子为0.95。从图7c和图7d可以看出,在三晶粒交界处(晶粒1、11、14)存在较大的几何必需位错密度以及明显的刚体转动张量。图7e为晶粒11内沿–线的位错密度。点和点之间的位错密度主要是由基面<>位错与锥面<+>位错构成。值得注意的是,晶粒11内的平均基面位错密度为1×1013m−2,约为–间锥面位错4.9× 1012m−2的2倍。一般认为,镁中锥面位错的临界剪切应力远大于基面位错的临界剪切应力,晶粒11内较高的位错密度反映了变形时材料内部复杂的应力状态。

图6 拉伸至6%后晶粒18表面的滑移带以及位错密度分布情况

图7 拉伸至6%后晶粒11表面的滑移带以及位错密度分布情况


图8 拉伸至6%后晶粒32表面的滑移带以及位错密度分布情况
2.2 Mg–Gd–Y–Zn合金中的应变调节机制
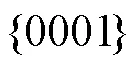
以上结果表明,稀土镁合金内调节应变的方式主要为基面位错以及锥面位错。现有研究表明,室温下在纯镁中的锥面位错会分解为基面不可动位错(pyramidal-to-basal transition),因此纯镁的塑性很差[7-8]。<+>滑移系的开动可以归因于稀土镁合金中I1型堆垛层错能(堆积序列为…ABABCBCB…)随着稀土元素的加入而降低,I1型堆垛层错成为<+>滑移系开动的位错源[16-17]。添加稀土元素后,锥面位错可以发生交滑移或双交滑移,从而有效避免了锥面位错的分解(PB transition),进而调节了密排六方结构轴方向的应变。

图9 稀土镁合金中基面位错密度与锥面位错密度与晶粒取向的关系
3 结论
采用原位拉伸和高分辨EBSD相结合的方法,系统研究了Mg–5.4Gd–1.8Y–1.5Zn(质量分数)锻造镁合金中的应变调节机制。将试样拉伸至应变6%,测量了试样内部的刚体转动张量以及几何必需位错密度,得出以下结论。
1)Mg–Gd–Y–Zn合金在拉伸过程中,晶界处的几何必需位错密度和刚体转动张量较大,尤其是三晶粒交界处。
2)Mg–Gd–Y–Zn合金中的应变主要由基面<>滑移系与锥面<+>滑移系来调节。
3)软取向晶粒内出现的锥面位错说明由于邻近晶粒的相互作用,局部应力张量对滑移活动有很大影响。
4)当发生基面–基面位错的滑移转移与基面–锥面位错的滑移转移时,相邻两晶粒滑移系之间的Luster–Morris因子很高(>0.78)。
[1] PROUST G. Processing Magnesium at Room Temperature[J]. Science, 2019, 364(6448): 30-31.
[2] WANG Xiao-jun, XU Dao-kui, WU Rui-zhi, et al. What is Going on in Magnesium Alloys[J]. Journal of Materials Science & Technology, 2018(2): 245-247.
[3] TRANG T T T, ZHANG J H, KIM J H, et al. Designing a Magnesium Alloy with High Strength and High Formability[J]. Nat Commun, 2018, 9(1): 2522.
[4] AGNEW S R. Deformation Mechanisms of Magnesium Alloys[J]. Advances in Wrought Magnesium Alloys, 2012: 63-104.
[5] BOEHLERT C, CHEN Z, GUTIÉRREZ-URRUTIA I, et al. In Situ Analysis of the Tensile and Tensile-Creep Deformation Mechanisms in Rolled AZ31[J]. Acta Materialia, 2012, 60(4): 1889-1904.
[6] AGNEW S R. Connections between the Basal I1 “Growth” Fault and 〈+〉 Dislocations[J]. Acta Materialia, 2015, 82: 255-265.
[7] WU Z. The Origins of High Hardening and Low Ductility in Magnesium[J]. Nature, 2015, 526: 62.
[8] AHMAD R. Designing High Ductility in Magnesium Alloys[J]. Acta Materialia, 2019, 172: 161-184.
[9] OROZCO-CABALLERO A. How Magnesium Accommodates Local Deformation Incompatibility: A High-Resolution Digital Image Correlation Study[J]. Acta Materialia, 2017, 133: 367-379.
[10] CALLISTER W D, RETHWISCH D G. Materials Science and Engineering 9th Edition[M]. Hoboken: John Wiley & Sons, 2013: 120-122.
[11] HIRSCH J, AL-SAMMAN T. Superior Light Metals by Texture Engineering: Optimized Aluminum and Magnesium Alloys for Automotive Applications[J]. Acta Materialia, 2013, 61(3): 818-843.
[12] WU D, CHEN R, HAN E. Excellent Room-Temperature Ductility and Formability of Rolled Mg-Gd-Zn Alloy Sheets[J]. Journal of Alloys and Compounds, 2010, 509(6): 2856-2863.
[13] CHEN Wen-zhen, ZHANG Wen-cong, QIAO Yan-dang, et al. Enhanced Ductility in High-Strength Fine-Grained Magnesium and Magnesium Alloy Sheets Processed via Multi-Pass Rolling with Lowered Temperature[J]. Journal of Alloys and Compounds, 2016, 665: 13-20.
[14] NAKATA T. New Mg-Al Based Alloy Sheet with Good Room-Temperature Stretch Formability and Tensile Properties[J]. Scripta Materialia, 2020, 180: 16-22.
[15] BIAN M. A Room Temperature Formable Magnesium-Silver-Calcium Sheet Alloy with High Ductility[J]. Materials Science and Engineering: A, 2020, 774: 138923.
[16] SANDLÖBES S, ZAEFFERER S, SCHESTAKOW I, et al. On the Role of Non-Basal Deformation Mechanisms for the Ductility of Mg and Mg-Y Alloys[J]. Acta Materialia, 2011, 59(2): 429-439.
[17] SANDLÖBES S. The Relation between Ductility and Stacking Fault Energies in Mg and Mg-Y Alloys[J]. Acta Materialia, 2012, 60(6): 3011-3021.
[18] WU B, ZHAO Y, DU X, et al. Ductility Enhancement of Extruded Magnesium via Yttrium Addition[J]. Materials Science & Engineering A, 2010, 527(16): 4334-4340.
[19] ZHANG D. TEM Study on Relationship between Stacking Faults and Non-Basal Dislocations in Mg, Philosophical Magazine[J]. Philosophical Magazine, 2015, 95(34): 3823-3844.
[20] SANDLÖBES S, PEI Z, FRIÁK M, et al. Ductility Improvement of Mg Alloys by Solid Solution: Ab Initio Modeling, Synthesis and Mechanical Properties[J]. Acta Materialia, 2014, 70: 92-104.
[21] XU C, FAN G H, NAKATA T, et al. Deformation Behavior of Ultra-Strong and Ductile Mg-Gd-Y-Zn-Zr Alloy with Bimodal Microstructure[J]. Metallurgical and Materials Transactions, 2018, 49(5): 1931-1947
[22] WILLIAMS D B, CARTER C B. Using Convergent-Beam Techniques[M]. Berlin: Springer, 2009: 347-368.
[23] WILKINSON A J, DINGLEY D J. Strain Mapping Using Electron Backscatter Diffraction[M]. Berlin: Springer, 2009: 231-249.
[24] TAMURA N, CELESTRE R S, MACDOWELL A A, et al. Submicron X-Ray Diffraction and Its Applications to Problems in Materials and Environmental Science[J]. Review of Scientific Instruments, 2002, 73(3): 1369-1372.
[25] FONZO S, JARK W, LAGOMARSINO S, et al. Non-Destructive Determination of Local Strain with 100-Nanometre Spatial Resolution[J]. Nature, 2000, 403(6770): 638-640.
[26] WILKINSON A J, MEADEN G, DINGLEY D J. High-Resolution Elastic Strain Measurement from Electron Backscatter Diffraction Patterns: New Levels of Sensitivity[J]. Ultramicroscopy, 2006, 106(4/5): 307-313.
[27] GUO Y, BRITTON T, WILKINSON A. Slip Band-Grain Boundary Interactions in Commercial-Purity Titanium[J]. Acta Materialia, 2014, 76: 1-12.
[28] VILALTA-CLEMENTE A, NARESH-KUMAR G, NOUF-ALLEHIANI M, et al. Cross-Correlation Based High Resolution Electron Backscatter Diffraction and Electron Channelling Contrast Imaging for Strain Mapping and Dislocation Distributions in InAlN Thin Films[J]. Acta Materialia, 2017, 125: 125-135.
[29] BRITTON T B, WILKINSON A J. Stress Fields and Geometrically Necessary Dislocation Density Distributions near the Head of a Blocked Slip Band[J]. Acta Materialia, 2012, 60(16): 5773-5782.
[30] ABDOLVAND H. Assessment of Residual Stress Fields at Deformation Twin Tips and the Surrounding Environments[J]. Acta Materialia, 2016, 105: 219-231.
Precise Measurement of Strain Accommodation in a Mg-Gd-Y-Zn Alloy
HAN Yan-bin1, JIANG Shao-song2, LI Yang2
(1. AVIC Xi'an Aircraft Industry Group Company Ltd., Xi'an 710089, China; 2. Harbin Institute of Technology, School of Materials Science and Engineering, Harbin 150001, China)
Mg-RE alloys show improved ductility compared to other classical magnesium alloys at room temperature. The present study focused on the strain accommodation mechanism in a wrought Mg-5.4Gd-1.8Y-1.5Zn alloy at the microstructural scale. For this purpose, a tensile specimen was uniaxially strained in-situ to 6%, and the lattice rotation tensor and geometrically necessary dislocation (GND) density were measured using cross-correlation-based high angular resolution electron backscatter diffraction (HR-EBSD) technique. The strain incompatibility within the Mg-Gd-Y-Zn alloy was accommodated by basal slip together with pyramidal dislocation. The GND measurements via HR-EBSD showed a high occurrence of pyramidal <+> dislocation even in well-aligned grains. In addition, slip transfer process of the basal-basal and basal-pyramidal type was observed with high Luster-Morris factors (>0.78), in this study. The average GND density in grains tends to decrease with the Schmid factor increases. This phenomenon can be attributed to the fact that more strain energy is consumed for the hard-oriented grains, which is stored in grains in the form of dislocation density during deformation.
strain accommodation; Mg-RE alloy; HR-EBSD; slip transfer; dislocation density
10.3969/j.issn.1674-6457.2022.06.001
TG146.2+2
A
1674-6457(2022)06-0001-09
2021–10–20
国家自然科学基金(51775135)
韩艳彬(1970—),男,博士,高级工程师,主要研究方向为镁铝合金在航空航天领域的轻量化应用。
蒋少松(1978—),男,博士,研究员,主要研究方向为轻质合金的超塑成形及应用。
责任编辑:蒋红晨

