双圈图的邻和可区别边染色
谭钧铭, 强会英, 刘欢, 王洪申
1.兰州交通大学 数理学院,兰州 730070;2.兰州理工大学 机电工程学院,兰州 730050

图G表示一个双圈图,图上的树的高度称为双圈图的有根树的高度.树上最长路的长度,称为有根树的高.V(G),E(G),Δ(G)分别是图G的点集合、边集合、最大度.dG(v)表示在图G中点v的度,Sφ(v)表示在φ下所有与点v相关联的边所染颜色构成的色集合,[k]表示{1,2,…,k}组成的色集合.GΔ表示图G的全体最大度顶点在图G中的导出子图.文中未加说明的符号可参见文献[9-12].
1 预备知识

定义2[14]边数等于顶点数加1的简单连通图叫做双圈图.
定义3设图H是无悬挂点的双圈图,则H∈{H1,H2,H3,H4,H5}.

图1 无悬挂点的双圈图




2 主要结论
定理1记树高都为0的双圈图分别为H1,H2,H3,H4,H5(如图1所示),则


表1 H1的邻和可区别边染色
现需证当r,s≡1(mod 3),t≡0(mod 3)或r,s≡1(mod 3),t≡2(mod 3)时,H1无3-NSDPEC.
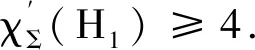

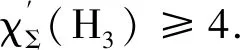

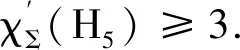

若r≢1(mod 3)且s≢1(mod 3).给出H5的一个3-NSDPEC:路xw1…wt-1y依次循环染1,2,3.令ywt-1染a,且{1,2,3}{a}={b,c}.当s≡0(mod 3)时,圈yv1…vs-1y依次循环染c,a,b;当s≡2(mod 3)时,圈yv1…vs-1y依次循环染b,c,a.圈xu1…ur-1x与yv1…vs-1y的染法相似.定理1成立.
将有根树的树高大于0且Δ(G)=3的双圈图分为3种:α-型双圈图,β-型双圈图,γ-型双圈图.
α-型双圈图:设图G是n阶双圈图(n≥16),且同时满足:(a)Δ(G)=3,GΔ=∅;(b) 图G是在H1的基础上连接着树,且在连接(x,y)的3条路中,有任意2条路的路长都恒等于1(mod 3),另一条路的路长恒等于2(mod 3);(c) 在路长恒等于2(mod 3)的路中,存在内点z,使得(x,z)与(z,y)的路长均为1(mod 3);(d) 任意v∈V(H1)z,dG(v)=dH1(v).
β-型双圈图:设图G是n阶双圈图(n≥10),且同时满足:(a)Δ(G)=3,GΔ=∅;(b)G中存在圈C,该圈圈长为r(r≡1(mod 3)),且圈上仅有1个3 度点.
γ-型双圈图:除α-型双圈图、β-型双圈图之外的Δ(G)=3的n阶(n≥4)双圈图.
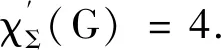

情形1 有根树最大高度为1.
若图G是α-型双圈图.记路P1的长r≡1(mod 3),路P2的长s≡1(mod 3),路P3的长t≡2(mod 3).在表1中r,s≡1(mod 3),t≡2(mod 3)时4-NSDPEC的基础上,给出G的一个4-NSDPEC:因GΔ=∅,故t≥8.在H1中,点z与其圈上的2个邻点的色集合分别是{1,2},{1,3},{2,3},则给z的悬挂边染3即可.
若图G是β-型双圈图.G只能由H5连接悬挂边所得,且悬挂边不可能同时在G的2个圈长都恒为1(mod 3)的圈上,也不可能在圈长为3的圈上,有可能在路w2…wt-2(t≥4)上.给G增加悬挂边,使G的3条路的所有顶点都有悬挂边(记该图为G0).在定理1的H5的4-NSDPEC的基础上,给出G0的一个4-NSDPEC:路u2…ur-2上的ui(2≤i≤r-2)的悬挂边染4;路v2…vs-2上的vi(i≡2(mod 3))的悬挂边染3,其他点的悬挂边染2;路w2…wt-2上的wi(2≤i≤t-2)的悬挂边染4.
现在去掉所有添加的悬挂边,容易得到图G的一个4-NSDPEC.
情形2 有根树最大高度大于1.
选树上具有最大高度的路,其悬挂点为v.v的邻点w不在圈上,w仅有一个非悬挂邻点u.反证法:设G是一个极小反例,即G是Δ(G)=3,且使|V(G)|+|E(G)|最小的不存在4-NSDPEC的图,则G的任意真子图G′有一个4-NSDPECφ′.令G′=G-wv,下面在G′的基础上,给边wv染色,将φ′拓展为G的4-NSDPECφ.
若dG(w)≠dG(u),则给边wv正常边染色就会使w与u邻点可区别.又因为dG(w)≤3,dG′(w)≤2,故在φ′下,w至少有2色未表现,总有一种色给wv,使得w与u邻和可区别,得到G的一个4-NSDPEC.与G是极小反例矛盾.
若dG(w)=dG(u)=2,则给边wv染上G′中点u未表现的色,即可使得w与u邻和可区别,得到G的一个4-NSDPEC.与G是极小反例矛盾.
综上所述,定理2成立.
定理3若图G是γ-型双圈图,则
证记图Gi是在Hi的基础上连接有根树得到的双圈图,因为Δ(G)=3,故i≠3.
情形1 有根树最大高度为1.
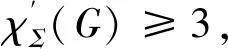
当G=G1时,根据图H1的3条路的路长,分以下几种情况讨论:
1) 若H1的3条路的路长是表1中除r,s≡1(mod 3),t≡0(mod 3)或r,s≡1(mod 3),t≡2(mod 3)之外的8种情况,则在定理1中H1的3-NSDPEC的基础上,给G所有悬挂边正常边染色,使G中所有3度点的色集合都是{1,2,3},即得到G的一个3-NSDPEC.
2) 若H1的3条路的路长是r,s≡1(mod 3),t≡0(mod 3)的情况.图G的悬挂点可以在P1,P2或P3上.
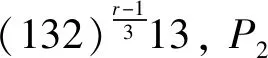

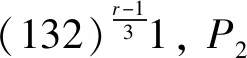
3)若图H1的3条路的路长是r,s≡1(mod 3),t≡2(mod 3)的情况,证明方法与r,s≡1(mod 3),t≡0(mod 3)的情况类似.
当G=G5时,方法与G=G1时类似.



2) 当H1是r,s≡1(mod 3),t≡0(mod 3)情况时,给P1上的ur-1的悬挂边染3,其他点的悬挂边染4.给P2上的vs-1的悬挂边染3,点vi(i≡2(mod 3))的悬挂边染2,其他点的悬挂边染4.给P3上的wt-1的悬挂边染3,其他点的悬挂边染4.
3) 当H1是r,s≡1(mod 3),t≡2(mod 3)的情况时,给wt-1的悬挂边染2,vs-1的悬挂边染1,其他悬挂边染4.
去掉所有添加的悬挂边,即得到G1的一个4-NSDPEC.

去掉所有添加的悬挂边,即得到G2的一个4-NSDPEC.若G=G4或G=G5,染法类似.

选树上有最大高度的路,其悬挂点为v.v的邻点w不在圈上,w仅有一个非悬挂邻点u.令G′=G-wv,下面在G′的基础上,给wv染色,将φ′拓展为G的s-NSDPECφ.

当dG(w)≠dG(u)时,若dG(w)=3,则给wv正常边染色,必有fφ(w)≠fφ(u);若dG(w)=2,则dG′(w)=1,在G′中w有2色未表现,故总有1色给wv,使得fφ(w)≠fφ(u),从而得到图G的一个3-NSDPEC.与G是最小反例矛盾.
当dG(w)=dG(u)时,给wv染上u未在G′表现的色,即得到G的一个3-NSDPEC.与G是最小反例矛盾.

当dG(w)≠dG(u)时,因dG(w)≤3,dG′(w)≤2,则在G′中w至少有2色未表现,则总有1色给wv,使得fφ(w)≠fφ(u),从而得到G的一个4-NSDPEC.与G是最小反例矛盾.
当dG(w)=dG(u),且φ′的点w表现的色都在u上表现时,则给wv染上u未在G′中表现的色,即可得到图G的一个4-NSDPEC.与G是最小反例矛盾.
当dG(w)=dG(u),且φ′的点w表现的某色没在u上表现时,由于dG(w)≤3,dG′(w)≤2,则在G′中w至少有2色未表现,总有1色给wv,使得fφ(w)≠fφ(u),从而得到G的一个4-NSDPEC.与G是最小反例矛盾.
综上所述,定理3成立.
定理4若图G是Δ(G)≥4的,且有根树最大高度大于0的双圈图,则
证记图Gi是在Hi(1≤i≤5)的基础上连接有根树得到的双圈图.
情形1 若有根树的最大高度为1,则根据有根树的位置和圈上相邻点的度分3种情况讨论.
情形1.1 图H上所有2度点z在图G中的度也为2,即dH(z)=dG(z)=2.则悬挂边只能在x或y处.不妨设dG(x)=k,dG(y)=l,且k≥l≥1.

又因为k≥l≥1,故dG(x)=Δ(G),则对点x的所有悬挂边正常边染色就能使得点x与x的邻点邻和可区别,即得到图G的一个Δ(G)-NSDPEC.
当G=Gi(2≤i≤5)时,方法与G=G1类似.
情形1.2 图H上存在2度点z,使得dH(z)=2且dG(z)≥3,且对任意满足该条件的点z,有dG(z)=dG(z′)=dG(z″).其中z′,z″是z在H上的2个邻点.


图2 满足情形1.2与情形1.3(2)的双圈图的基本结构
令G′=G-zz1-zz2,对zz1,zz2重新染色x1,x2.f′(z)表示在G′中z的色集合的所有元素的加和.边zz1,zz2可用颜色集分别为S1,S2,由正常边染色的条件得
|S1|=|S2|=(Δ(G)+1)-(Δ(G)-2)=3
再由邻和可区别边染色的条件得
Q(x1,x2)=(x1-x2)(x1+x2+f′(z)-f(z′))(x1+x2+f′(z)-f(z″))
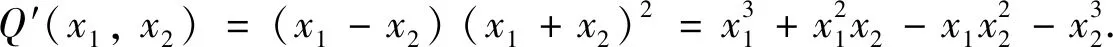
情形1.3 图H上存在一个2度点z,使得dH(z)=2且dG(z)≥3,且dG(z)≠dG(z′).其中z′,z″是点z在H上的2个邻点.

1) 当H=H3,Δ(G)=4,且x是G的唯一最大度点时.令G′=G-zv,zv是悬挂边.因3度点z与其邻点仅有1+2+3=2+4,1+2+4=3+4邻和相等的情况.故z与z′,z″的公共边染2,4,导致z最多与一个2度点邻和相等.在G′的4-NSDPEC的基础上,zv有2色未表现,则总存在1色给zv,得到G的一个4-NSDPEC.与G是最小反例矛盾.
2) 其他情况时,令G的最大度点为u,uv是悬挂边.令G′=G-uv,对uv正常边染色即得到G的一个Δ(G)-NSDPEC.与G是最小反例矛盾.

令G′=G-uu1,则对uu1重新染色x1.记uu1可用颜色集为S1.由正常边染色的条件得
|S1|=(Δ(G)+1)-(dG(u)-1)≥(Δ(G)+1)-(Δ(G)-2)=3
再由邻和可区别边染色的条件得
Q(x1)=(x1+f′(u)-f(u′))(x1+f′(u)-f(u″))


情形2 有根树的最大高度大于1.

选树上具有最大高度的路,其悬挂点为v.点v的邻点w不在圈上,且w仅有1个非悬挂邻点u.令G′=G-wv,下面在G′的基础上,给边wv染色,将φ′拓展为G的s-NSDPECφ.

当dG(w)≠dG(u)时,给wv正常边染色可使Sφ(w)≠Sφ(u).故给wv染色时,只需考虑fφ(w)与fφ(u)是否相等.若dG(w)=Δ(G),给wv正常边染色,必有fφ(w)≠fφ(u);若dG(w)≤Δ(G)-1,则dG′(w)≤Δ(G)-2,即在G′中w至少有2色未表现,且最多有1色给wv,使得fφ(w)=fφ(u).故总有1色给wv,使得w与u邻和可区别,从而得到G的一个Δ(G)-NSDPEC.与G是最小反例矛盾.
当dG(w)=dG(u),且φ′的点w表现的色都在u上表现时,给边wv染上点u未在φ′中表现的色,即可得到图G的一个Δ(G)-NSDPEC.与G是最小反例矛盾.
当dG(w)=dG(u),且φ′的点w表现的某色未在u上表现时,由于dG(w)≤Δ(G)-1,则dG′(w)≤Δ(G)-2,即在G′中w至少有2色未表现,且最多有1色给wv,使得fφ(w)=fφ(u).故总有1色给wv,使得w与u邻和可区别,从而得到G的一个Δ(G)-NSDPEC.与G是最小反例矛盾.

综上所述,定理4成立.

