亚正规对偶截断Toeplitz算子
丁宣浩, 黄雨浩, 桑元琦, 李永宁
1.重庆工商大学 数学与统计学院,重庆 400067;2.经济社会应用统计重庆市重点实验室,重庆 400067;3.西南财经大学 经济数学学院,成都 611130
记H2表示开单位圆盘D={z∈C:|z|<1}上的Hardy空间,L2=L2(T)是单位圆周T={z∈C:|z|=1}上的平方可积函数构成的空间,L∞表示由T上全体本性有界函数构成的空间,H∞是D上有界解析函数构成的全体.
对于每一个非常值的内函数u,我们称
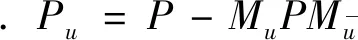
Tfx=P(fx)x∈H2
模型空间正交补上的对偶截断Toeplitz算子Df定义为
文献[1-2]发现对偶截断Toeplitz算子与Hardy空间上的Toeplitz算子[3]有许多相同的性质.例如:对偶截断Toeplitz算子是有界的当且仅当其符号是有界的;紧的对偶截断Toeplitz算子只能是零算子;对偶截断Toeplitz算子为零算子当且仅当其符号为零;符号为连续函数的对偶截断Toeplitz算子生成的C*-代数模去紧算子后构成的理想*-等距同构于T上的连续函数全体[2].
因此,我们特别考虑是否Df是次正规算子当且仅当Tf是次正规算子?
为了说明我们的研究动机,首先来回顾次正规算子的定义以及Halmos第五问题的历史.
对于Hilbert空间H上的算子S,如果S存在一个包含H的Hilbert空间K,且其上的正规算子N满足S=N|H,则称S为次正规算子.次正规算子理论在许多问题中都有广泛应用[4].文献[5]对Toeplitz算子提出了著名的Halmos第五问题“是否次正规Toepltiz算子不是解析的就是正规的?” 文献[6]给出了Halmos第五问题成立的充分条件.文献[7]认为这个猜测几乎是正确的.然而,Halmos第五问题首先被我国著名算子理论学家孙顺华先生解决[8-9].此外,文献[10]也对这个问题进行了研究.但是至今数学家无法给出次正规Toeplitz算子的符号刻画.
对偶截断Toeplitz算子与Toeplitz算子有许多差异.文献[11]的定理9证明了两个解析Toeplitz算子的乘积还是Toeplitz算子.然而,我们很容易构造出两个解析对偶截断Toeplitz算子,其乘积不是对偶截断Toeplitz算子[1].更多关于Toeplitz算子和Hankel算子的相关研究可参见文献[12-13].
本文的第一部分,我们考虑了对偶截断Toeplitz算子版本的Halmos第五问题,证明了不存在解析的次正规对偶截断Toeplitz算子.本文的第二部分,我们完全刻画了亚正规的对偶截断Toeplitz算子.
1 解析对偶截断Toeplitz算子
令Mf为L2上的乘法算子,定义为
Mfφ=fφ
Mf正是解析Toeplitz 算子Tf的正规延拓.因此,Hardy空间H2上每一个解析的Toeplitz算子Tf都是次正规的.Df(f是解析函数)在uH2上的限制Df|uH2是次正规的,但是我们不知道解析对偶截断Toeplitz算子是否是次正规的.因此我们考虑如下的问题:
问题1是否每个解析对偶截断Toeplitz算子都是次正规的?
下面的定理1将给出问题1的否定回答.
定理1如果f是一个非常数的解析函数,则Df不是次正规的.
证假设Df是次正规的,则存在正规延拓N,使得
此外,N+λI也是正规算子,并且满足
其中λ是常数.因此,Df+λI是次正规的.不失一般性,假设f(0)=0.令f=zf1,其中f1∈H2.因为次正规算子必是亚正规的,所以Df是亚正规的.Hilbert空间H上的算子T为亚正规算子当且当
T*T≥TT*
当且当
‖Tx‖≥‖T*x‖ ∀x∈H
因为
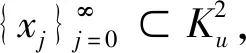
和
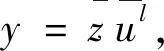
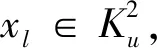
因此
进一步,
矛盾,则
2 亚正规对偶截断Toeplitz算子
因为每个解析对偶截断Toeplitz算子不是次正规的,我们将对偶截断Toeplitz算子的Halmos第五问题改写为如下形式:
问题2是否每个次正规的对偶截断Toeplitz算子都是正规的?
首先,我们用复对称算子的方法给出问题2的肯定回答.然后,运用经典的Toeplitz算子理论,完全刻画正规对偶截断Toeplitz算子的符号.
对于Hilbert 空间上的算子T,存在一个等距且共轭线性的对合映射C,使得
3.因果式(前因后果或前果后因)。如竺可桢的《沙漠里的奇怪现象》,文章从沙漠中的奇怪现象入手,揭示了光线、声音作怪的奥秘。
CTC=T*
在L2上有一个经典的对合映射C,其定义为
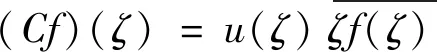
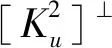
定理2如果f∈L∞,则下面的3条陈述是等价的:
证⟺由上面的讨论,我们知道亚正规的对偶截断Toeplitz算子都是正规的.反过来,根据定义,每个正规算子一定是亚正规的.
(1)
展开(1)式可得
(2)
取y=ux,x∈H2,则(2)式变为
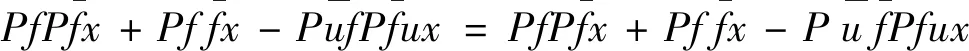
(3)
因此
根据文献[3]的命题7.5,可得
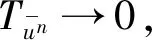
则
进一步有
(4)
计算下式
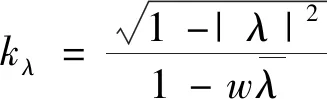
由(4)式可得
类似地,有
因此
注1Hardy空间上的Toeplitz算子反酉等价于(H2)⊥上的对偶Toeplitz算子(H2)⊥[18-19].
但是对于模型空间的情况就完全不同了,对偶截断Toeplitz算子Df是正规的当且当Tf是正规的(定理2),当且当存在常数c和d以及一个实值函数φ∈L∞,满足f=cφ+d.正规截断Toeplitz算子与正规对偶截断Toeplitz算子的符号有巨大区别,并且是复杂的[20-21].

